5
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Случаи приведения и уравнения равновесия систем сил презентация
Содержание
- 1. Случаи приведения и уравнения равновесия систем сил
- 2. ТЕОРЕМА ПУАНСО (ОСНОВНАЯ ТЕОРЕМА СТАТИКИ) Основная теорема
- 3. ТЕОРЕМА ПУАНСО (ОСНОВНАЯ ТЕОРЕМА СТАТИКИ) Основная теорема
- 4. СТАТИЧЕСКИЕ ИНВАРИАНТЫ Статические инварианты – характеристики системы
- 5. СТАТИЧЕСКИЕ ИНВАРИАНТЫ Главный момент не является
- 6. СТАТИЧЕСКИЕ ИНВАРИАНТЫ Случаи приведения Умножим равенство скалярно
- 7. СТАТИЧЕСКИЕ ИНВАРИАНТЫ Случаи приведения Второй статический инвариант
- 8. ДИНАМИЧЕСКИЙ ВИНТ Случаи приведения Динамический винт –
- 9. ТЕОРЕМА О ДИНАМИЧЕСКОМ ВИНТЕ Случаи приведения Если
- 10. СЛУЧАИ ПРИВЕДЕНИЯ СИСТЕМ СИЛ Случаи приведения динамический винт равнодействующая пара сил система сил уравновешена
- 11. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛА Условия равновесия система
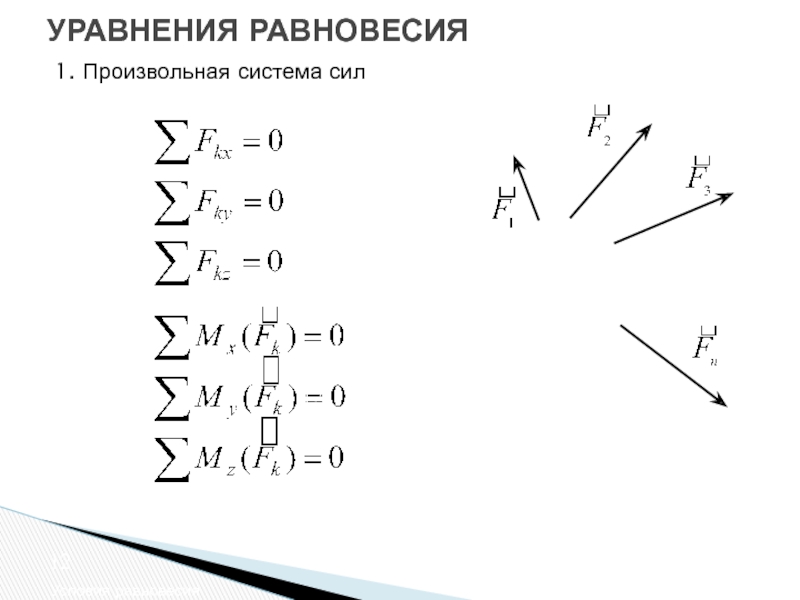
- 12. УРАВНЕНИЯ РАВНОВЕСИЯ Условия равновесия 1. Произвольная система сил
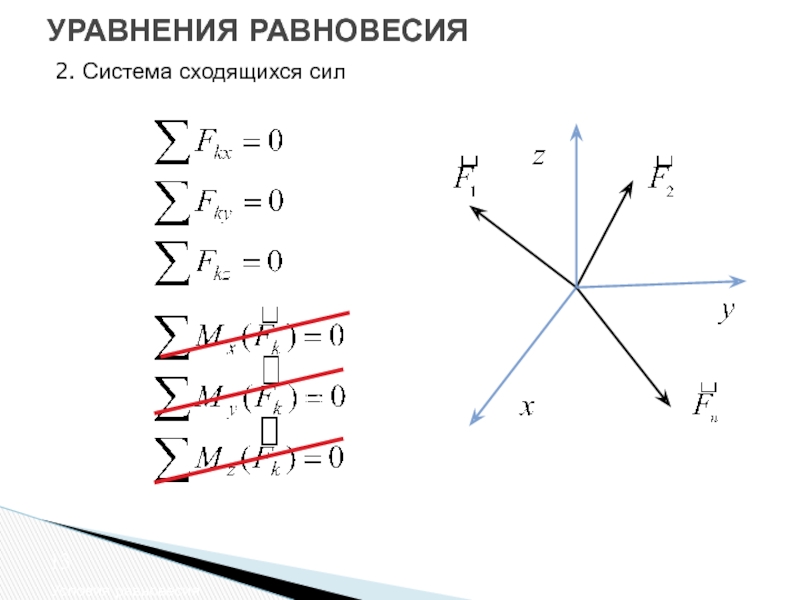
- 13. УРАВНЕНИЯ РАВНОВЕСИЯ Условия равновесия 2. Система сходящихся сил
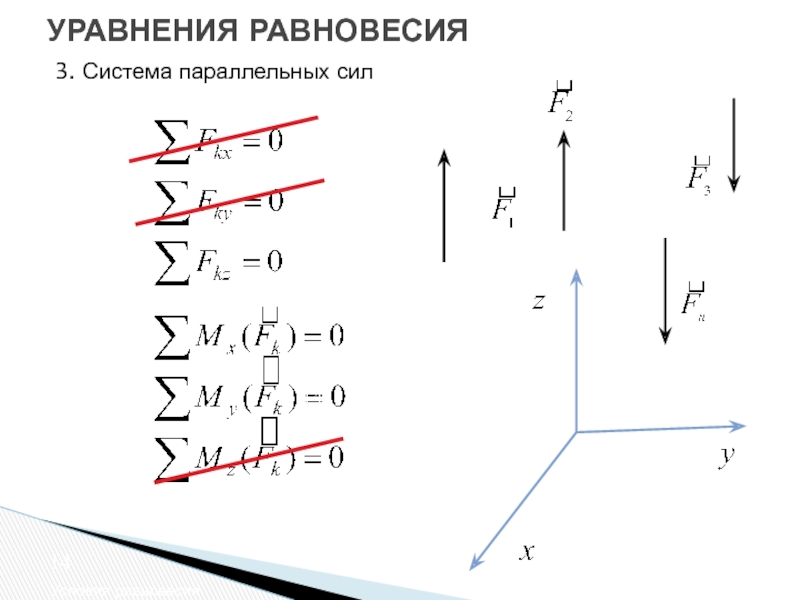
- 14. УРАВНЕНИЯ РАВНОВЕСИЯ Условия равновесия 3. Система параллельных сил
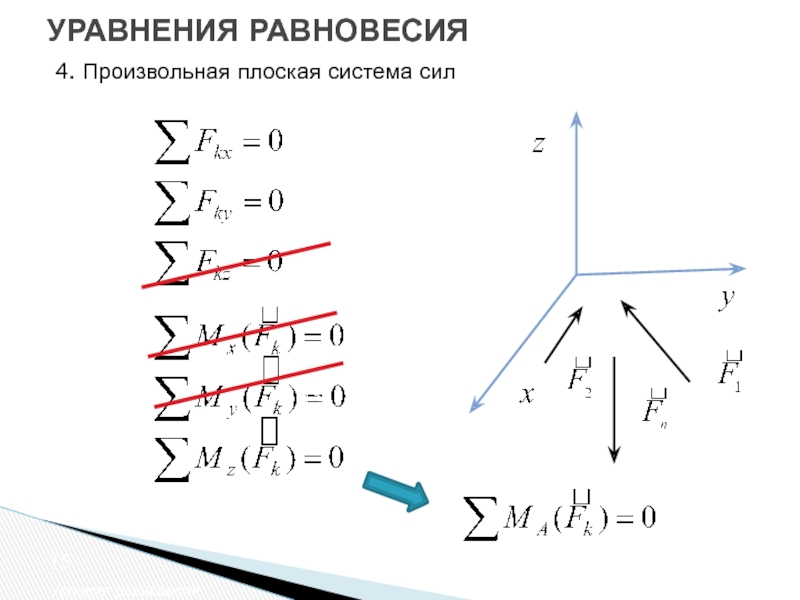
- 15. УРАВНЕНИЯ РАВНОВЕСИЯ Условия равновесия 4. Произвольная плоская система сил
- 16. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА Условия
- 17. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА Условия
- 18. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА Условия
- 19. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА Условия
- 20. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА Условия
ТЕОРЕМА ПУАНСО (ОСНОВНАЯ ТЕОРЕМА СТАТИКИ) Основная теорема статики Произвольная система сил эквивалентна силе, равной главному вектору системы, и паре сил, момент которой равен главному моменту системы относительно точки приложения силы (центра
Слайд 1СЛУЧАИ ПРИВЕДЕНИЯ И УРАВНЕНИЯ РАВНОВЕСИЯ
СИСТЕМ СИЛ
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
СТАТИКА
ЛЕКЦИЯ
Слайд 2ТЕОРЕМА ПУАНСО (ОСНОВНАЯ ТЕОРЕМА СТАТИКИ)
Основная теорема статики
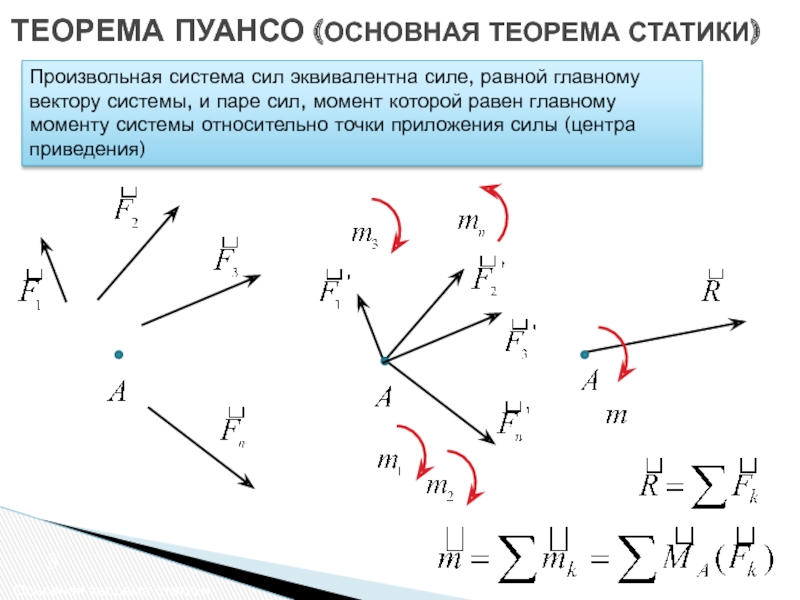
Произвольная система сил эквивалентна силе,
равной главному вектору системы, и паре сил, момент которой равен главному моменту системы относительно точки приложения силы (центра приведения)
Луи́ Пуансо́ (1777-1859) —французский математик и механик, академик Парижской Академии наук(1813); пэр Франции (1846), сенатор (1852). Известен своими трудами в области геометрии и механики
Слайд 3ТЕОРЕМА ПУАНСО (ОСНОВНАЯ ТЕОРЕМА СТАТИКИ)
Основная теорема статики
Произвольная система сил эквивалентна силе,
равной главному вектору системы, и паре сил, момент которой равен главному моменту системы относительно точки приложения силы (центра приведения)
Слайд 4СТАТИЧЕСКИЕ ИНВАРИАНТЫ
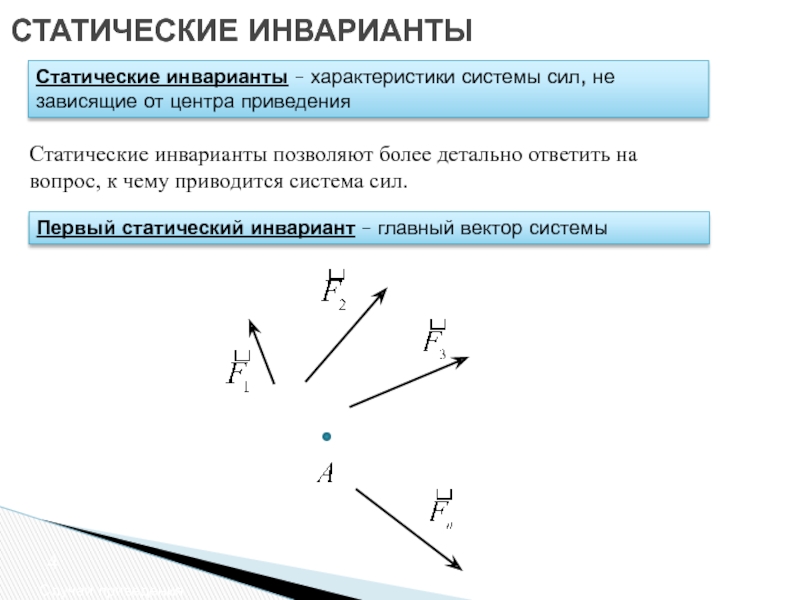
Статические инварианты – характеристики системы сил, не зависящие от центра
приведения
Статические инварианты позволяют более детально ответить на вопрос, к чему приводится система сил.
Первый статический инвариант – главный вектор системы
Случаи приведения
Слайд 5СТАТИЧЕСКИЕ ИНВАРИАНТЫ
Главный момент не является статическим инвариантом.
Как он зависит от
центра приведения?
Определим момент одной из сил системы
Главный момент системы
Случаи приведения
Слайд 6СТАТИЧЕСКИЕ ИНВАРИАНТЫ
Случаи приведения
Умножим равенство скалярно
на главный вектор системы
Последнее слагаемое равно
нулю (почему?)
Второй статический инвариант – скалярное произведение главного вектора на главный момент
Слайд 7СТАТИЧЕСКИЕ ИНВАРИАНТЫ
Случаи приведения
Второй статический инвариант – минимальный главный момент
Получили альтернативное определение
Как
найти минимальный главный момент?
Слайд 8ДИНАМИЧЕСКИЙ ВИНТ
Случаи приведения
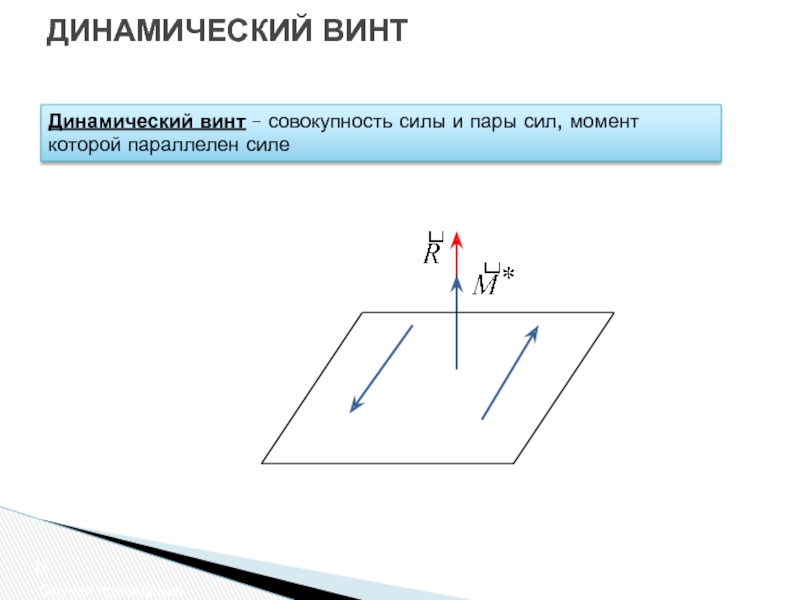
Динамический винт – совокупность силы и пары сил, момент
которой параллелен силе
Слайд 9ТЕОРЕМА О ДИНАМИЧЕСКОМ ВИНТЕ
Случаи приведения
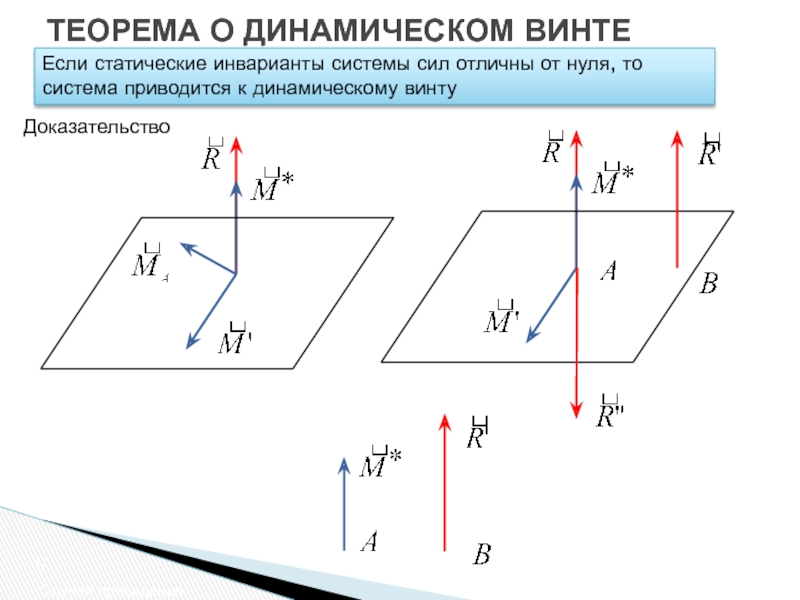
Если статические инварианты системы сил отличны от
нуля, то система приводится к динамическому винту
Доказательство
Слайд 10СЛУЧАИ ПРИВЕДЕНИЯ СИСТЕМ СИЛ
Случаи приведения
динамический винт
равнодействующая
пара сил
система сил уравновешена
Слайд 11УСЛОВИЯ РАВНОВЕСИЯ ТЕЛА
Условия равновесия
система сил уравновешена
АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ГЛАВНОГО ВЕКТОРА И
ГЛАВНОГО МОМЕНТА
Слайд 16РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА
Условия равновесия
Опоры ЛЭП
Мосты
Подъемные
краны
Металлические
каркасы зданий
Слайд 17РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА
Условия равновесия
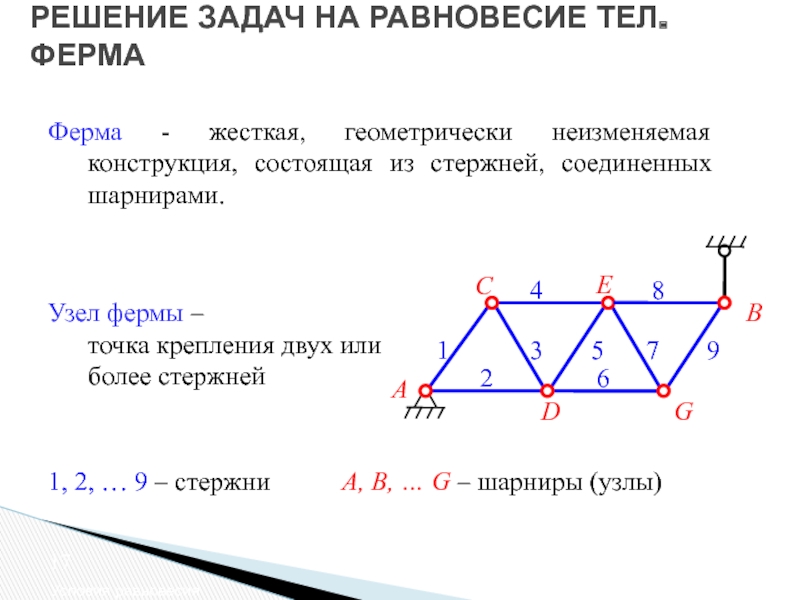
Ферма - жесткая, геометрически неизменяемая
конструкция, состоящая из стержней, соединенных шарнирами.
Узел фермы –
точка крепления двух или более стержней
1, 2, … 9 – стержни
A, B, … G – шарниры (узлы)
Слайд 18РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА
Условия равновесия
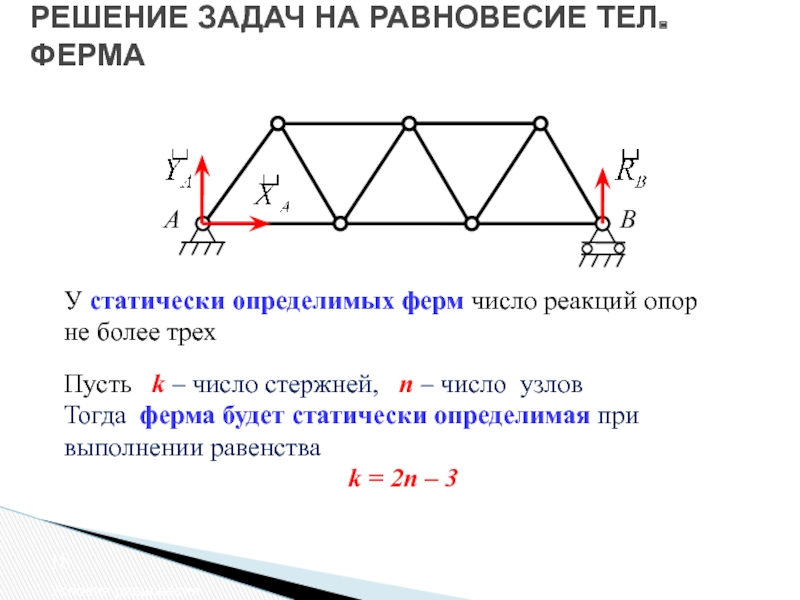
Пусть k – число
стержней, n – число узлов
Тогда ферма будет статически определимая при выполнении равенства
k = 2n – 3
Тогда ферма будет статически определимая при выполнении равенства
k = 2n – 3
У статически определимых ферм число реакций опор не более трех
Слайд 19РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА
Условия равновесия
Для расчета ферм необходимо
Найти реакции
внешних опор с использованием аксиомы отвердевания и 3-х уравнений равновесия
Определить усилия в стержнях фермы методом вырезания узлов или методом сечений ( Риттера)
Определить усилия в стержнях фермы методом вырезания узлов или методом сечений ( Риттера)
Слайд 20РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ТЕЛ. ФЕРМА
Условия равновесия
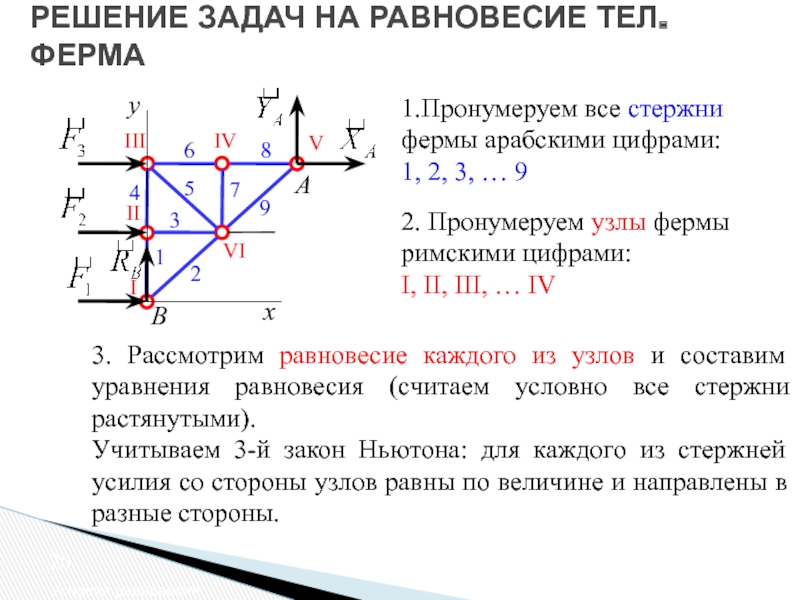
1.Пронумеруем все стержни фермы арабскими
цифрами:
1, 2, 3, … 9
2
3
4
5
6
7
8
9
1
I
II
III
IV
V
VI
3. Рассмотрим равновесие каждого из узлов и составим уравнения равновесия (cчитаем условно все стержни растянутыми).
Учитываем 3-й закон Ньютона: для каждого из стержней усилия со стороны узлов равны по величине и направлены в разные стороны.
2. Пронумеруем узлы фермы римскими цифрами:
I, II, III, … IV
