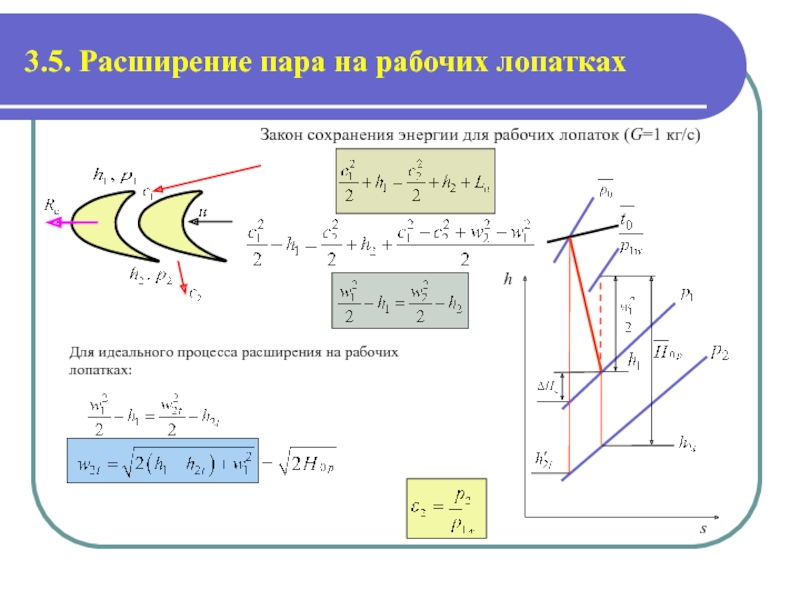
Для идеального процесса расширения на рабочих лопатках:
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расширение пара на рабочих лопатках презентация
Содержание
- 1. Расширение пара на рабочих лопатках
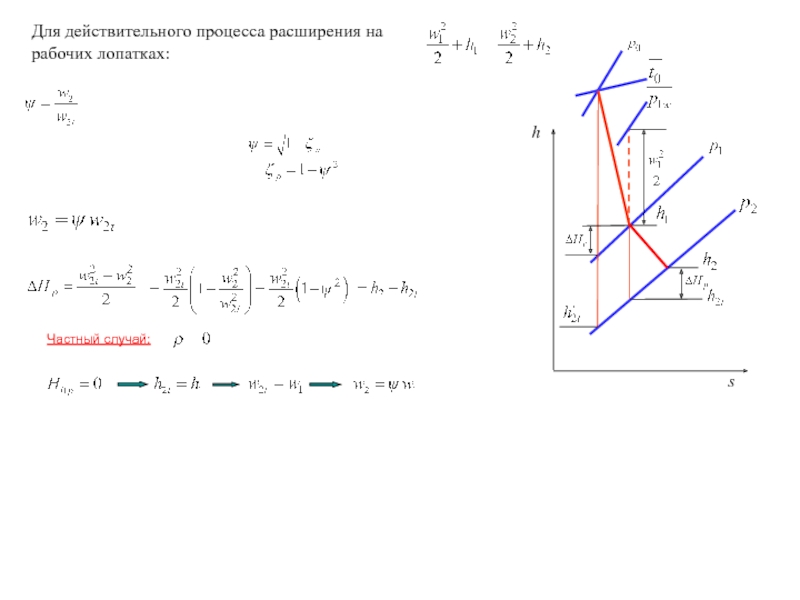
- 2. Частный случай: Для действительного процесса расширения на рабочих лопатках:
- 3. 3.6. Работа (мощность) 1 кг газа в
- 4. - потеря располагаемой энергии в соплах:
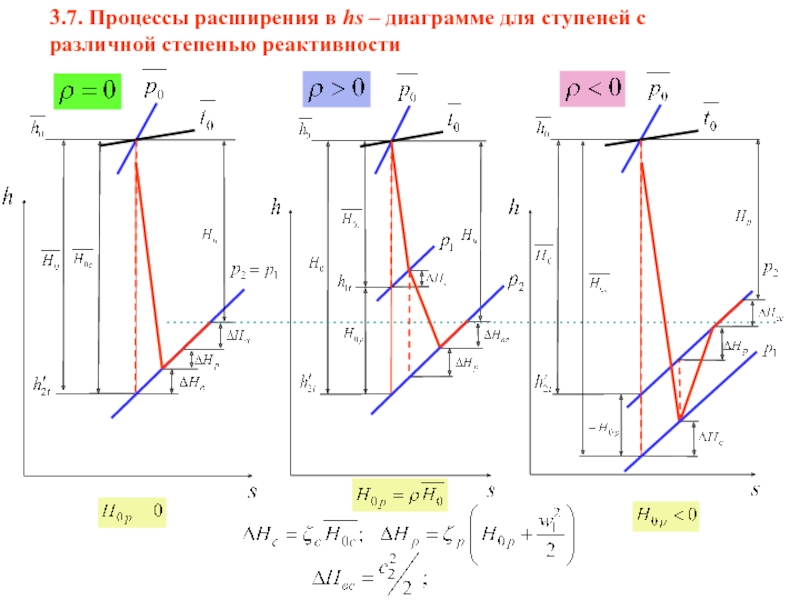
- 5. 3.7. Процессы расширения в hs – диаграмме для ступеней с различной степенью реактивности
- 6. 3.2. Относительный лопаточный
- 7. 3.2.1. Зависимость относительного лопаточного КПД от безразмерного
- 8. - безразмерное отношение
- 9. - безразмерное отношение
- 11. I. Примем тогда При II. III. IV.
- 12. Б. Для ступени при любом значении
- 13. 3.2.2. Оптимальный располагаемый теплоперепад ступени Задано:
Частный случай: Для действительного процесса расширения на рабочих лопатках:
Слайд 13.5. Расширение пара на рабочих лопатках
Закон сохранения энергии для рабочих лопаток
(G=1 кг/с)
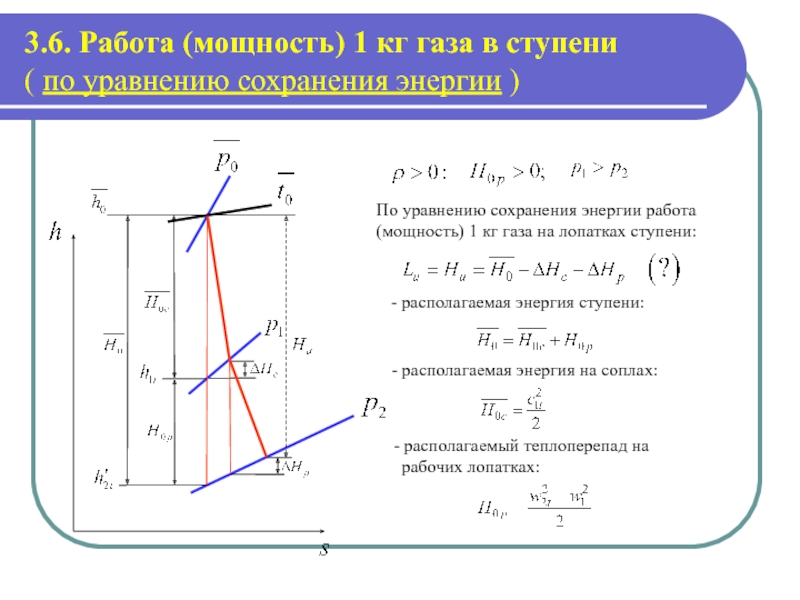
Слайд 33.6. Работа (мощность) 1 кг газа в ступени ( по уравнению
сохранения энергии )
По уравнению сохранения энергии работа (мощность) 1 кг газа на лопатках ступени:
- располагаемая энергия ступени:
- располагаемая энергия на соплах:
- располагаемый теплоперепад на рабочих лопатках:
Слайд 4
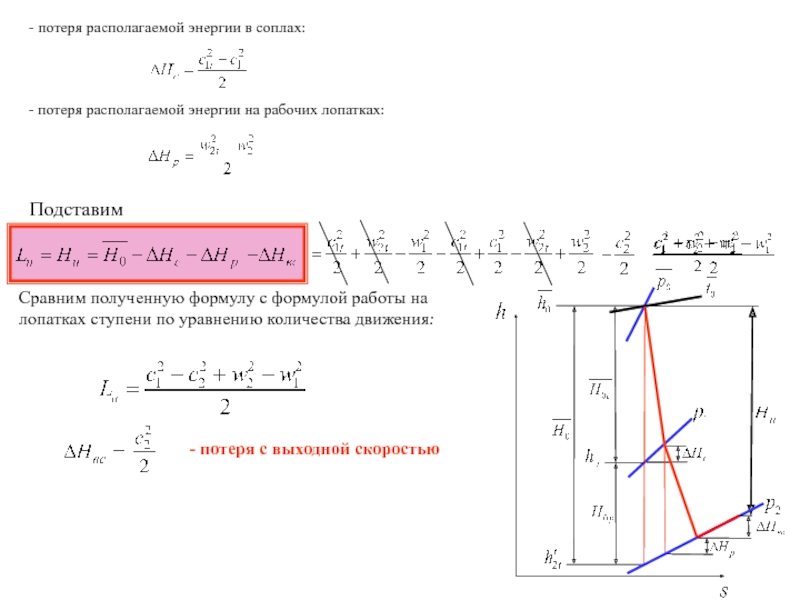
- потеря располагаемой энергии в соплах:
- потеря располагаемой энергии на рабочих
лопатках:
Подставим
Сравним полученную формулу с формулой работы на лопатках ступени по уравнению количества движения:
- потеря с выходной скоростью
Слайд 6
3.2. Относительный лопаточный КПД ступени
Характеризует совершенство (эффективность) процесса преобразования энергии в
проточной части ступени:
По определению понятия КПД
По уравнению сохранения энергии
По уравнению количества движения
фиктивная скорость в ступени, эквивалентная располагаемой энергии на ступень
По уравнению сохранения энергии
По уравнению количества движения
По уравнению количества движения
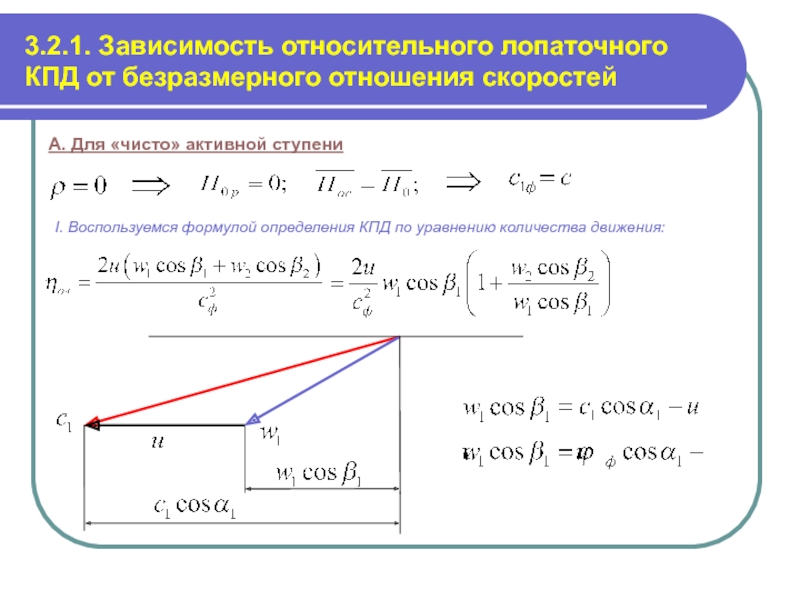
Слайд 73.2.1. Зависимость относительного лопаточного КПД от безразмерного отношения скоростей
А. Для «чисто»
активной ступени
I. Воспользуемся формулой определения КПД по уравнению количества движения:
Слайд 8
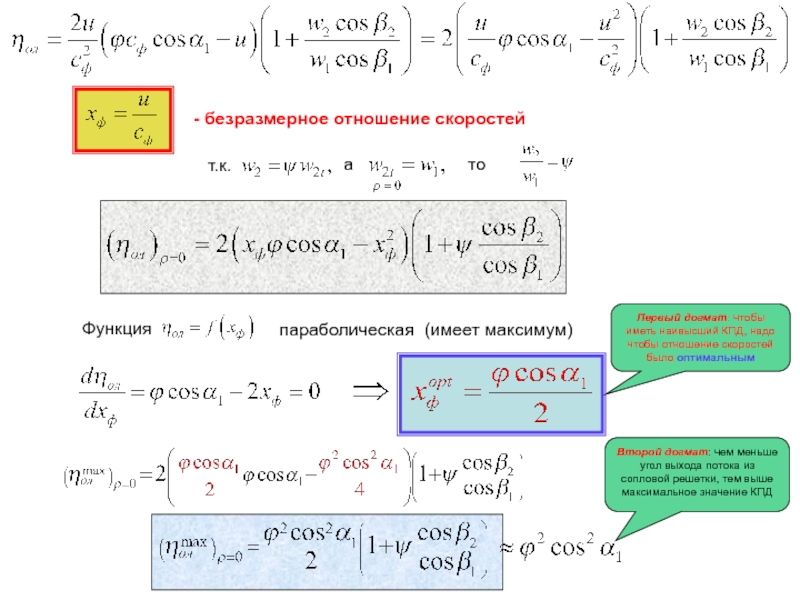
- безразмерное отношение скоростей
т.к.
а
то
Функция
параболическая
(имеет максимум)
Первый догмат: чтобы иметь наивысший КПД,
надо чтобы отношение скоростей было оптимальным
Второй догмат: чем меньше угол выхода потока из сопловой решетки, тем выше максимальное значение КПД
Слайд 9
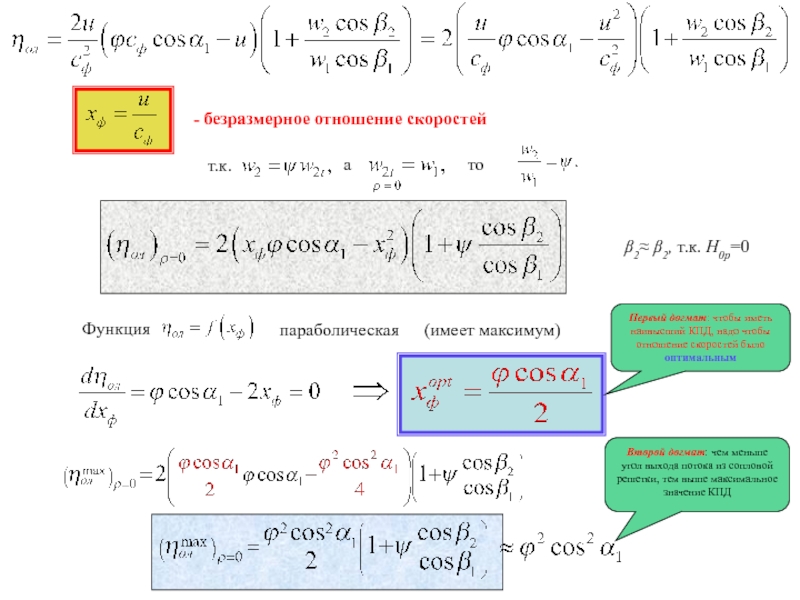
- безразмерное отношение скоростей
т.к.
а
то
Функция
параболическая
(имеет максимум)
Первый догмат: чтобы иметь наивысший КПД,
надо чтобы отношение скоростей было оптимальным
Второй догмат: чем меньше угол выхода потока из сопловой решетки, тем выше максимальное значение КПД
β2≈ β2, т.к. H0p=0
Слайд 10
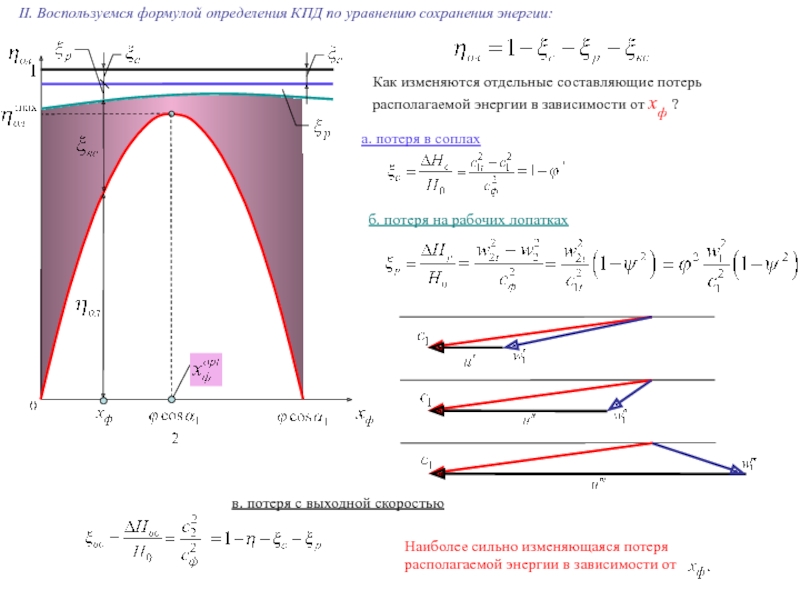
Как изменяются отдельные составляющие потерь
располагаемой энергии в зависимости от хф ?
a.
потеря в соплах
б. потеря на рабочих лопатках
в. потеря с выходной скоростью
Наиболее сильно изменяющаяся потеря располагаемой энергии в зависимости от
II. Воспользуемся формулой определения КПД по уравнению сохранения энергии:
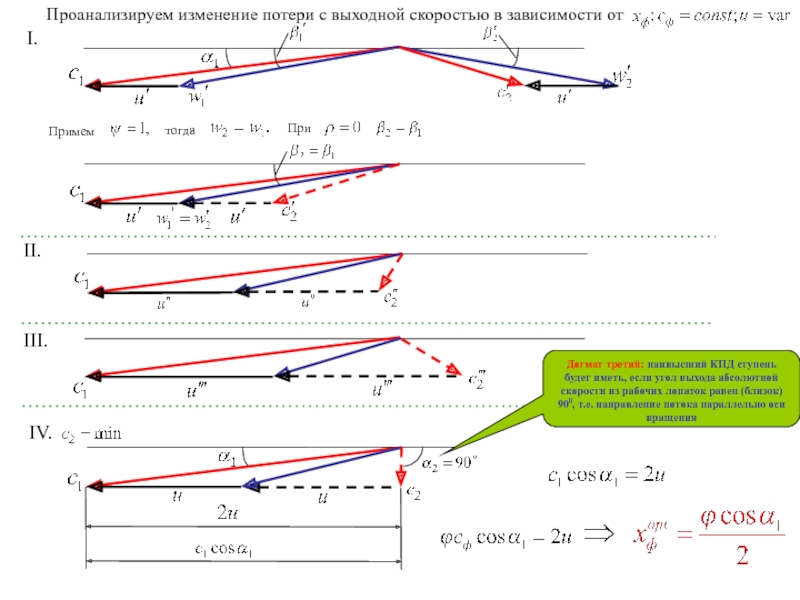
Слайд 11I.
Примем
тогда
При
II.
III.
IV.
Догмат третий: наивысший КПД ступень будет иметь, если угол выхода абсолютной
скорости из рабочих лопаток равен (близок) 900, т.е. направление потока параллельно оси вращения
Проанализируем изменение потери с выходной скоростью в зависимости от
Слайд 12
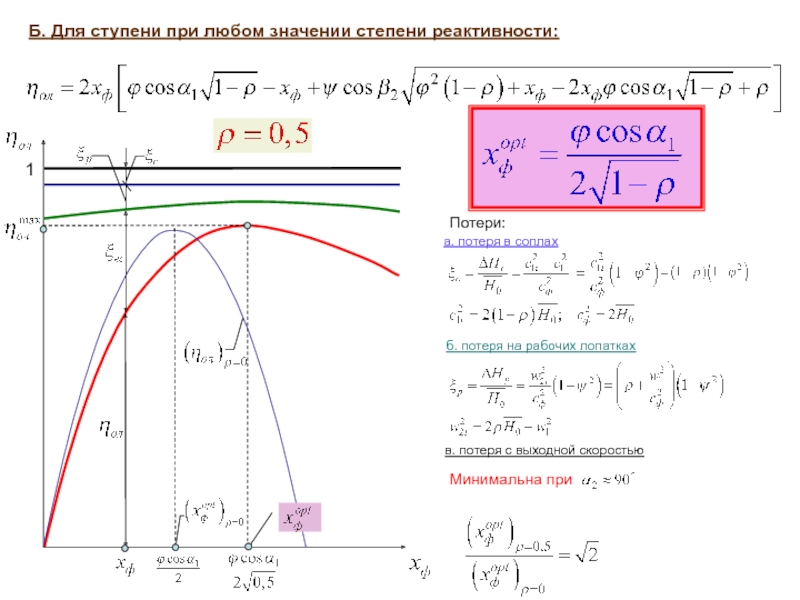
Б. Для ступени при любом значении степени реактивности:
1
Потери:
a. потеря в
соплах
б. потеря на рабочих лопатках
в. потеря с выходной скоростью
Минимальна при
Слайд 133.2.2. Оптимальный располагаемый теплоперепад ступени
Задано: диаметр ступени и угловая скорость вращения
ротора.
Определить: какой теплоперепад сработает ступень с наивысшим КПД.
Определить: какой теплоперепад сработает ступень с наивысшим КПД.
Частные случаи:
а)
б)
в)
