- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Распределение Больцмана. (Лекция 10) презентация
Содержание
- 1. Распределение Больцмана. (Лекция 10)
- 2. Лекция 10 Тема: РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
- 3. 10.1. Распределение Больцмана
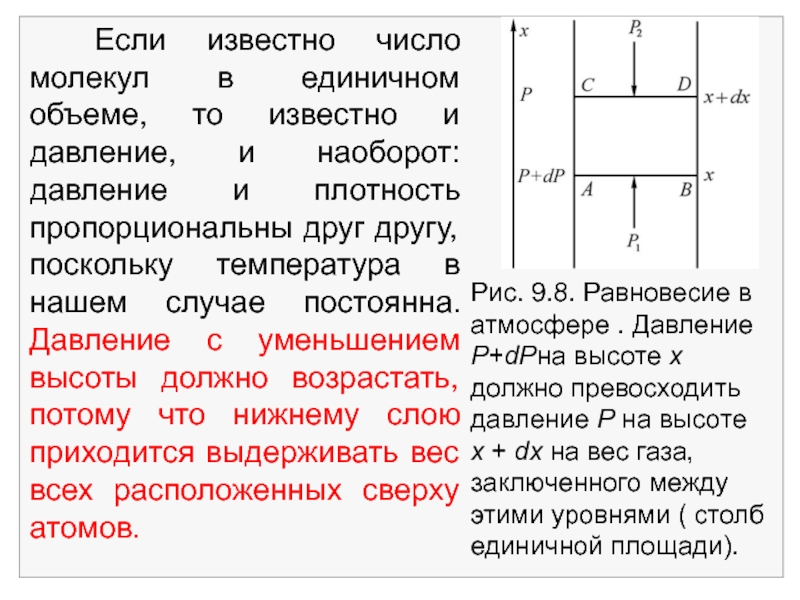
- 4. Рис. 9.8. Равновесие в
- 5. Найдем изменение концентрации газа с высотой
- 6. Приравнивая эти величины, имеем:
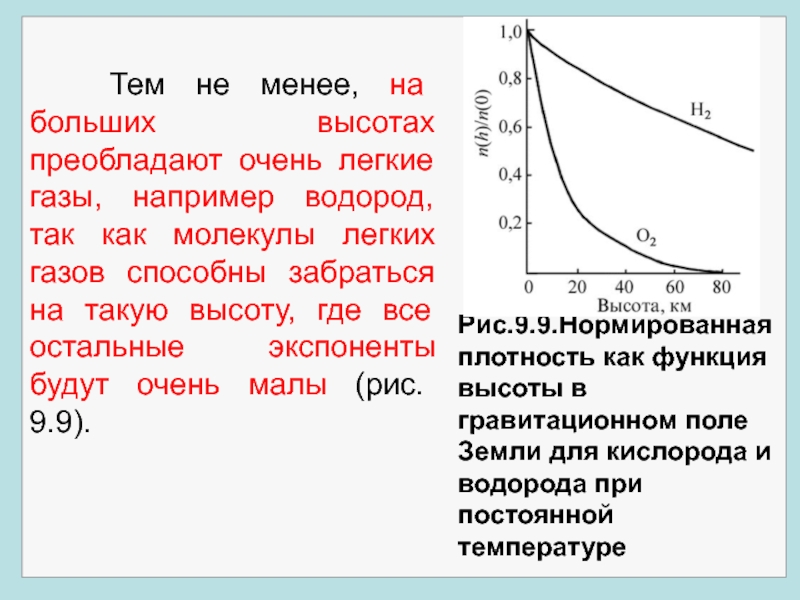
- 9. Тем не менее, на
- 10. Если энергии принимают набор дискретных значений
- 13. Рис. 9.10. Разделение частиц в центрифуге. При
- 26. Лекция окончена Нажмите клавишу для выхода
Слайд 1Томский политехнический университет
ФТИ
Адрес: пр. Ленина, 43, г.Томск, Россия, 634034
tyurin@fnsm.tpu.edu.ru,
Тел.
Факс 8-3822-563-403
Слайд 2
Лекция 10
Тема: РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
10.1. Распределение Больцмана
10.2. Разделение вещества на центрифуге
10.3.
проверка распределения
Больцмана и измерение
числа Авогадро в опытах
Перрена
Содержание лекции:
Сегодня: *
Слайд 4
Рис. 9.8. Равновесие в атмосфере . Давление Р+dPна высоте х должно
Слайд 5 Найдем изменение концентрации газа с высотой x в условиях теплового
dF = S⋅dx⋅n(x)⋅mg,
где S – площадь основания столба, n(x) – концентрация частиц на высоте x, m – масса одной частицы, g – ускорение силы тяжести. Вес столба уравновешивается силой разности давлений на высотах x и x + dx.
Слайд 6Приравнивая эти величины, имеем:
Подставляя сюда выражение для P(x)=n(x)kT и учитывая, что температура газа не изменяется с высотой, получим:
или
Если U – потенциальная энергия молекулы в силовом поле, то mgdx = dU(x) или, в случае неоднородного поля, m(g,dr) = dU(r), откуда следует
n(r) = n0exp ( -U(r)/kT).
Приравнивая эти величины, имеем:
dP/dx= −n(x)mg.
Подставляя сюда выражение для P(x)=n(x)kT и учитывая, что температура газа не изменяется с высотой, получим:
или
Если U – потенциальная энергия молекулы в силовом поле, то mgdx = dU(x) или, в случае неоднородного поля, m(g,dr) = dU(r), откуда следует
n(r) = n0exp ( -U(r)/kT).
Слайд 9
Тем не менее, на больших высотах преобладают очень легкие
Рис.9.9.Нормированная плотность как функция высоты в гравитационном поле Земли для кислорода и водорода при постоянной температуре
Слайд 10Если энергии принимают набор дискретных значений E1, E2, …,
Причем должно выполняться условие нормировки .
Откуда следует выражение для P(En):.
- статистическая сумма. С помощью Z вычисляют многие важнейшие величины статистической физики.
Слайд 13Рис. 9.10. Разделение частиц в центрифуге. При вращении центрифуги более тяжелые
На частицы примеси во вращающейся жидкости действует центробежная сила с учетом выталкивающей архимедовой силы, равная
.
Здесь μэфф = μ1(1 −ρ/ ρ1) эффективная молекулярная масса; V – объем одного моля.