- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение функций комплексного переменного презентация
Содержание
- 1. Применение функций комплексного переменного
- 2. Лекция 7 Плоское потенциальное движение
- 3. Применение функций комплексного переменного Как уже отмечали,
- 4. Применение функций комплексного переменного В теории функций
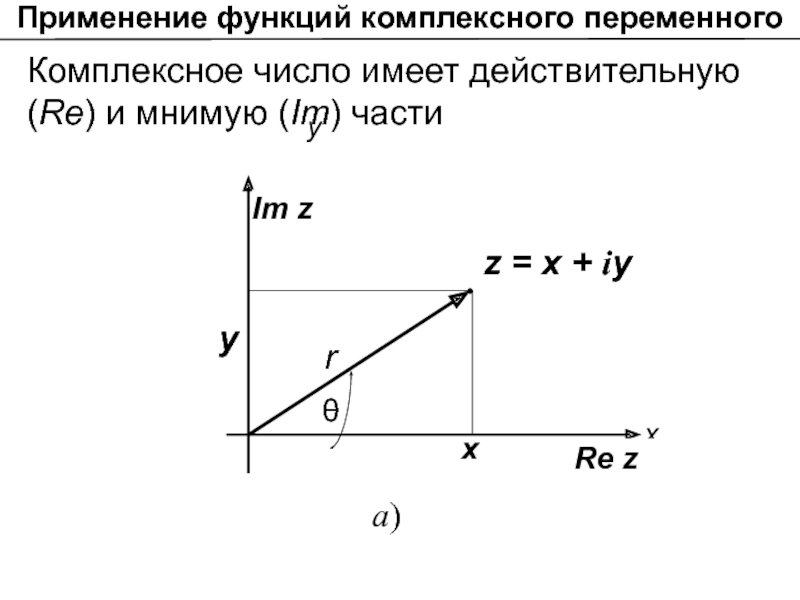
- 5. Применение функций комплексного переменного х Re z
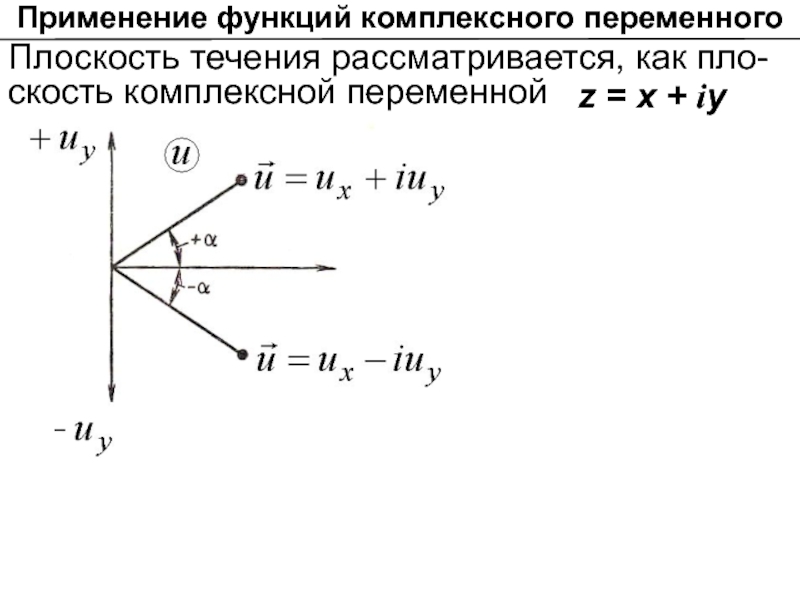
- 6. Применение функций комплексного переменного Плоскость течения рассматривается,
- 7. Комплексное число также можно изображать радиус-вектором. Длина
- 8. Применение функций комплексного переменного О комплексных числах
- 9. Модуль произведения (частного) двух комп- лексных чисел
- 10. Применение функций комплексного переменного
- 11. Для того, чтобы функция w (z)=
- 12. Применение функций комплексного переменного Такая функция называется
- 13. Применение функций комплексного переменного
- 14. действительная часть которой равна проекции скорости иx,
- 15. Применение функций комплексного переменного При сложении течений
- 16. Применение функций комплексного переменного В плоскости течения
- 17. (и =0) пересекаются две или несколько (конеч-ное
- 18. Применение функций комплексного переменного Величину
- 19. Во-вторых, можно, задавшись аналитической функцией W, выделить
- 20. Рассмотрим, как выразится комплексный потенциал для элементарных потоков.
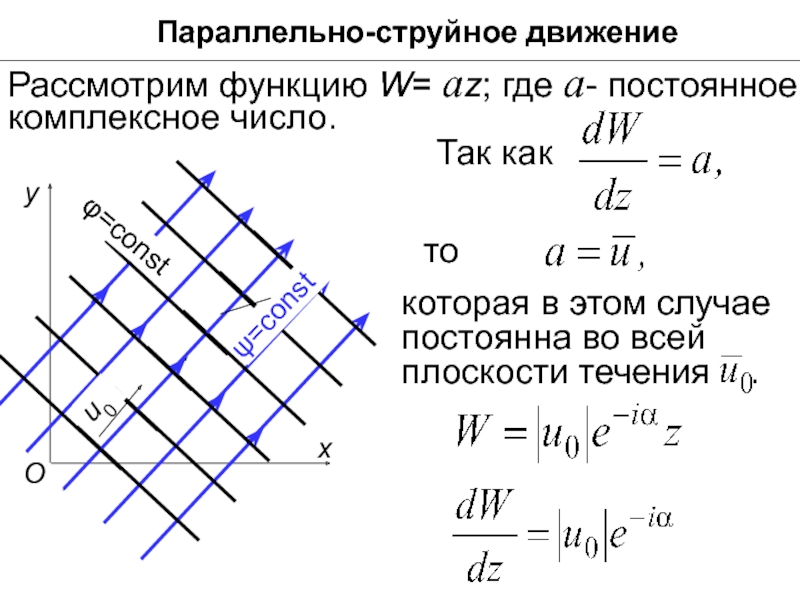
- 21. Параллельно-струйное движение Рассмотрим функцию W= az; где
- 22. Параллельно-струйное движение Вдоль линий тока ψ= const
- 23. Параллельно-струйное движение Эквипотенциали представляют собой дpyгoе семейство параллельных прямых, ортогональ-ное к первому.
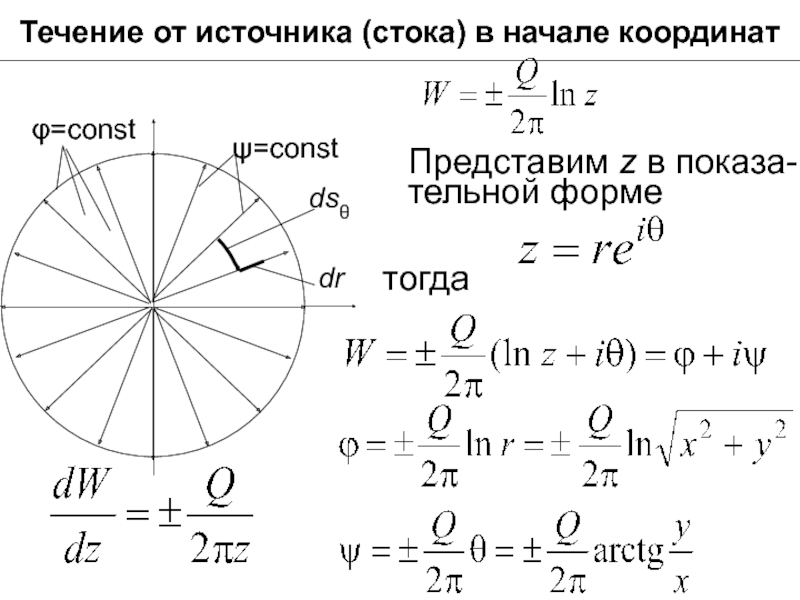
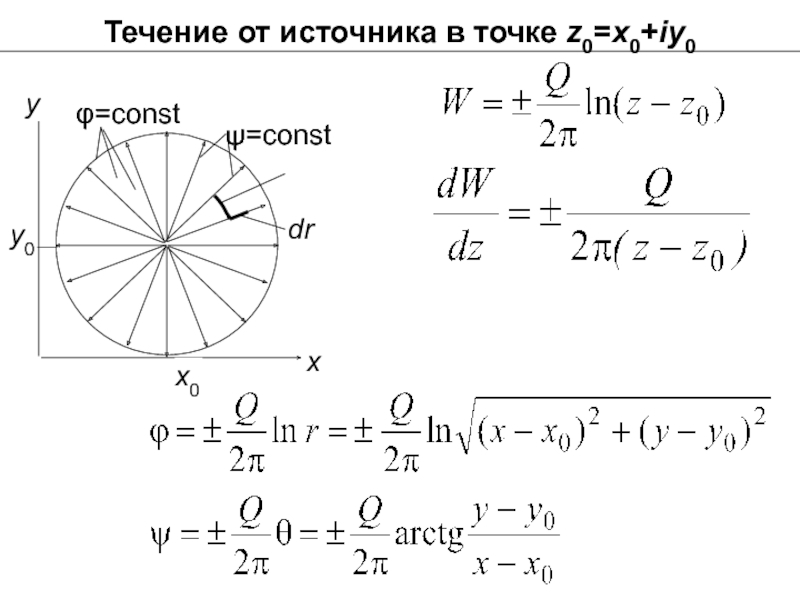
- 24. Течение от источника (стока) в начале координат dsθ Представим z в показа-тельной форме тогда
- 25. Течение от источника (стока) в начале координат
- 26. Течение от источника в точке z0=x0+iy0 ψ=const
- 27. Течение от вихря в точке z0=x0+iy0 y0 x x0 y0 y
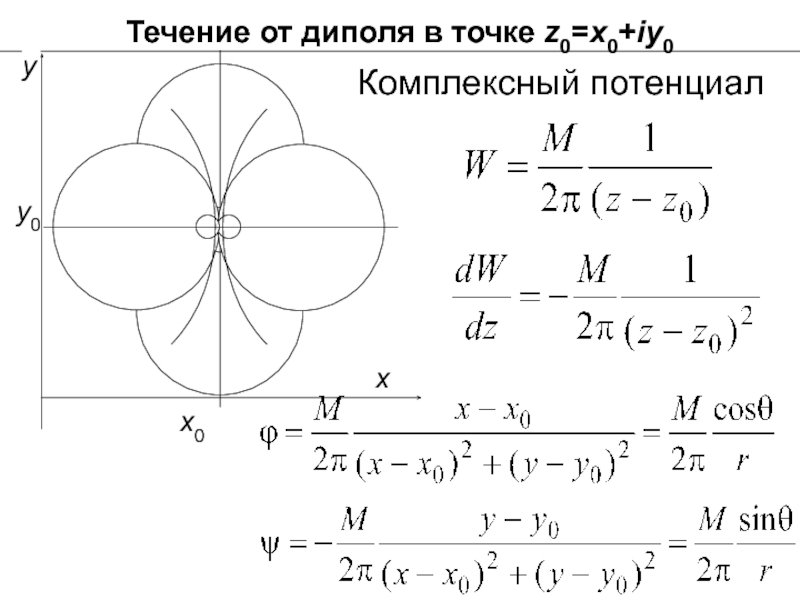
- 28. Течение от диполя в точке z0=x0+iy0 y0 x x0 y Комплексный потенциал
Слайд 3Применение функций комплексного переменного
Как уже отмечали, для для плоских потенци-альных течений
Эти уравнения дают возможность применить для описания потенциальных течений несжи-маемой жидкости, аппарат теории функции комплексного переменного
Слайд 4Применение функций комплексного переменного
В теории функций комплексного переменного доказывается, что если
w (z)= φ +iψ,
называемой комплексным потенциалом.
Эта функция обладает определенной конеч-ной производной во всех точках области, где определены φ и ψ .
Слайд 5Применение функций комплексного переменного
х
Re z
Im z
у
r
z = x + iy
θ
а)
Комплексное число
x
y
Слайд 6Применение функций комплексного переменного
Плоскость течения рассматривается, как пло-скость комплексной переменной
z
Слайд 7Комплексное число также можно изображать радиус-вектором. Длина радиус-вектора, изоб-
ражающего комплексное число
Применение функций комплексного переменного
Модуль вычисляется по формуле:
Слайд 8Применение функций комплексного переменного
О комплексных числах
Модуль любого ненулевого комплексного чис-
ла
Число называется комплексно-со-
пряженным числом к числу , т. е. комплексно сопряженные числа отличаются лишь знаком мнимой части.
z = x + iy
z = x - iy
Модули комплексно-сопряженных чисел равны.
Слайд 9Модуль произведения (частного) двух комп-
лексных чисел равен произведению (частно-
му) модулей каждого
Применение функций комплексного переменного
Аргумент θ комплексного числа связан с его действительной и мнимой частями соотноше-ниями:
Слайд 10Применение функций комплексного переменного
Тригонометрической формой комплексного числа называется
Показательной формой комплексного числа называется выражение
Слайд 11Для того, чтобы функция
w (z)= φ +iψ=φ(x,y)+iψ(x,y),
определенная в некоторой
φ(х, у) и ψ(x,y)
были дифференцируемы в той же точке и для них удовлетворялись уравнения Коши-Рима-на.
Применение функций комплексного переменного
Слайд 12Применение функций комплексного переменного
Такая функция называется аналитической. Следовательно, любую аналитическую функ-цию
Производная функции комплексного пе-
ременного считается существующей
лишь тогда, когда
не зависит от способа приближения Δz к нулю.
Слайд 14действительная часть которой равна проекции скорости иx, а мнимая – взятой
Производная комплексного потенциала по не-зависимой переменной представляет собой комплексную переменную
Применение функций комплексного переменного
Слайд 15Применение функций комплексного переменного
При сложении течений комплексные потенци-
алы суммируются:
W(z) = W1(z)
Производная функции течения в какой либо точке равна комплексной сопряженной скорости в этой точке.
Модуль этой пpoизводной дает абсолютную величину скорости, а аргумент, взятый с обратным знаком, определяет направление скорости в рассматриваемой точке.
Слайд 16Применение функций комплексного переменного
В плоскости течения могут находиться точки, в которых
В точках, где
может пересекаться бесконечно большое число линий тока. В этих точках распoлагa-ютcя источники, диполи, вихри.
Слайд 17(и =0) пересекаются две или несколько (конеч-ное число) линий тока. Эти
В точках, где
Применение функций комплексного переменного
Слайд 18Применение функций комплексного переменного
Величину называют сопряженной скopо-стью. В комплексной
которое называется комплексной скоростью.
Величины и и можно также представить в форме
Слайд 19Во-вторых, можно, задавшись аналитической функцией W, выделить в ней действительную и
А также найти
чем определится поле скоростей.
Применение функций комплексного переменного
Плоские течения с помощью комплексного потенциала можно изучать различно.
Во-первых, можно, задавшись конфигурацией линий тока или полем скоростей, отыскивать вид функций φ и ψ, W и .
Слайд 21Параллельно-струйное движение
Рассмотрим функцию W= az; где а- постоянное комплексное число.
Так
то
которая в этом случае постоянна во всей плоскости течения .
Слайд 22Параллельно-струйное движение
Вдоль линий тока ψ= const и, следовательно, их уравнение запишется,
Это уравнение семейства параллельных прямых, наклоненных к оси х, под углом α
Слайд 23Параллельно-струйное движение
Эквипотенциали представляют собой дpyгoе семейство параллельных прямых, ортогональ-ное к первому.
Слайд 25Течение от источника (стока) в начале координат
Линии тока (ψ= cоnst или
Проекции скорости в полярных координатах:
В поле источника (стока) скорость убывает об-ратно пропорционально расстоянию от центра.
Скорость, направленная от центра к периферии (источник), положительна, в этом случае Q >0. Стоку соответствует Q <0.