Эквивалентные участки электрических цепей обладают свойствами:
симметричности (если цепь А эквивалентна цепи Б, то цепь Б эквивалентна цепи А);
рефлексивности (цепь А является эквивалентной самой себе);
транзистивности (если цепь А эквивалентна цепи Б, а цепь Б эквивалентна цепи В, то цепи А и В являются эквивалентными).
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразования электрических цепей презентация
Содержание
- 1. Преобразования электрических цепей
- 2. ПРЕОБРАЗОВАНИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
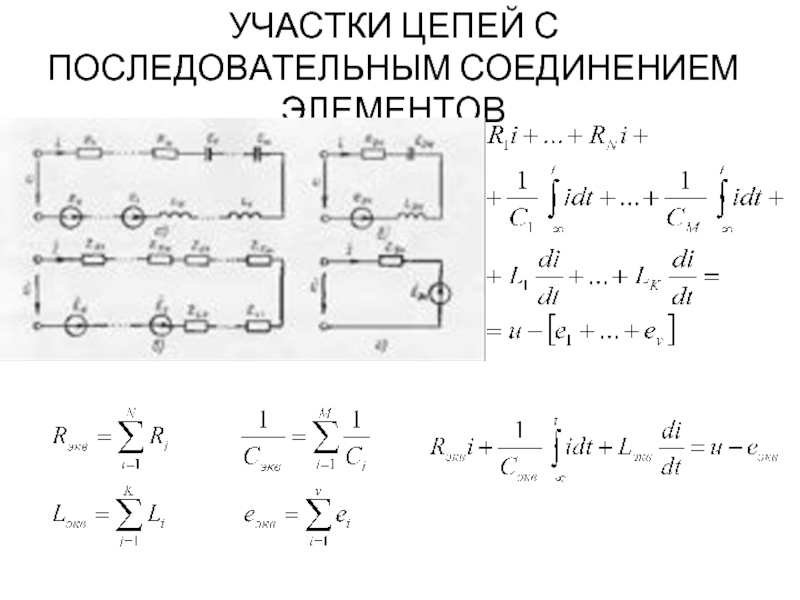
- 3. УЧАСТКИ ЦЕПЕЙ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
- 4. УЧАСТКИ ЦЕПЕЙ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
- 5. УЧАСТКИ ЦЕПЕЙ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
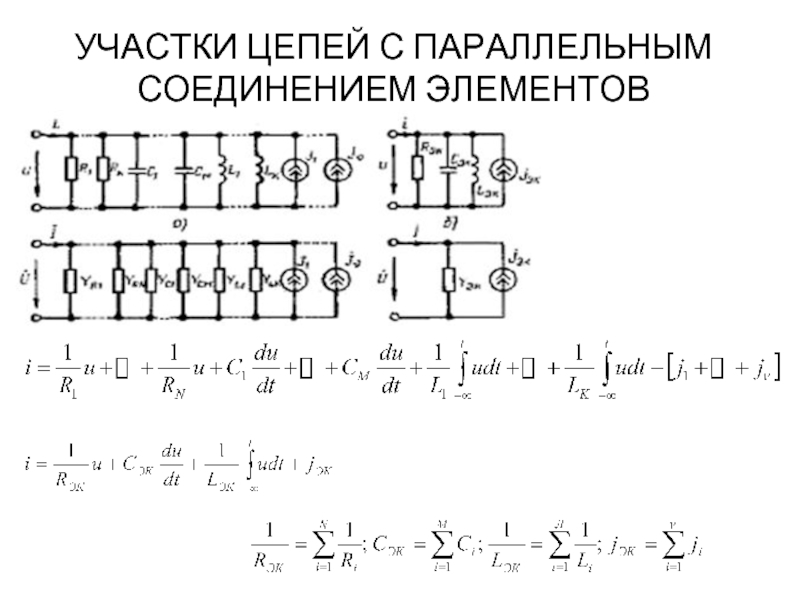
- 6. УЧАСТКИ ЦЕПЕЙ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
- 7. УЧАСТКИ ЦЕПЕЙ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
- 8. УЧАСТКИ ЦЕПЕЙ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
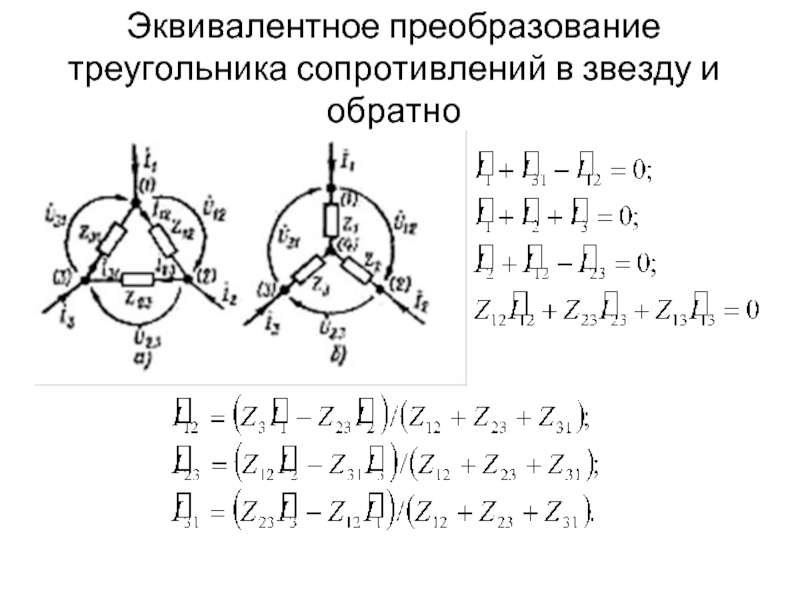
- 9. Эквивалентное преобразование треугольника сопротивлений в звезду и
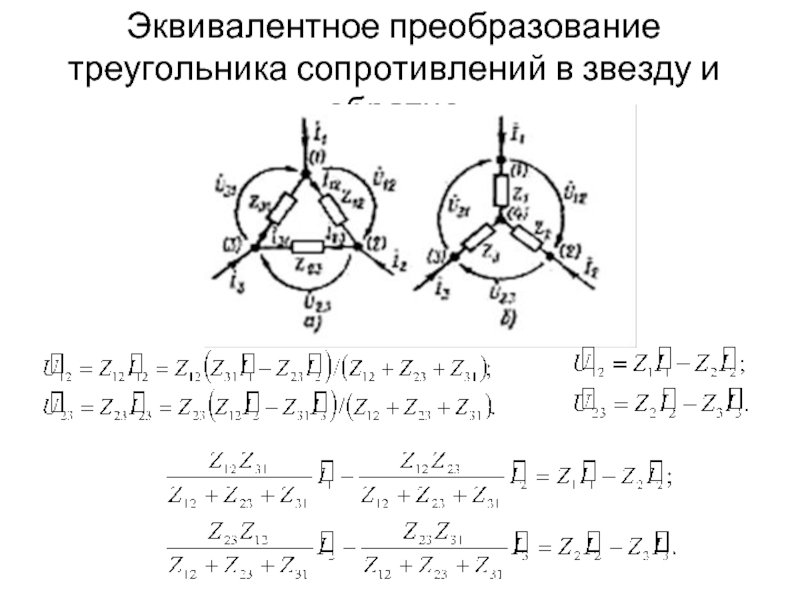
- 10. Эквивалентное преобразование треугольника сопротивлений в звезду и
- 11. Эквивалентное преобразование треугольника сопротивлений в звезду и
- 12. КОМПЛЕКСНЫЕ СХЕМЫ ЗАМЕЩЕНИЯ ИСТОЧНИКОВ ЭНЕРГИИ
Слайд 1ПРЕОБРАЗОВАНИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Два участка идеализированной электрической цепи называются эквивалентными, если при
Слайд 2ПРЕОБРАЗОВАНИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Если эквивалентность двух участков электрической цепи выполняется при любых
Если эквивалентность двух участков соблюдается только при определенном значении внешних воздействий, то такие участки являются частично эквивалентными (эквивалентными при заданных условиях).
Каждое равносильное преобразование системы уравнений электрического равновесия исходной цепи (приведение подобных членов, исключение неизвестных, замена переменных и т. д.) приводит к эквивалентному преобразованию моделирующей цепи.
Слайд 4УЧАСТКИ ЦЕПЕЙ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
При последовательном включении емкостей значение величины,
При последовательном включении сопротивлений, индуктивностей и источников напряжения параметры эквивалентного элемента Rэкв, Lэкв и eэкв равны сумме параметров последовательно включенных элементов соответствующего типа.
Слайд 5УЧАСТКИ ЦЕПЕЙ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
Таким образом, любой участок электрической цепи,
Слайд 7УЧАСТКИ ЦЕПЕЙ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
При параллельном включении емкостей и источников
При параллельном включении сопротивлений или индуктивностей значения величин, обратных Rэкв и Lэкв, определяются как сумма значений всех величин, обратных параллельно включенным сопротивлениям Ri или индуктивностям Li.
Слайд 8УЧАСТКИ ЦЕПЕЙ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
Таким образом, любой участок электрической цепи,
Слайд 11Эквивалентное преобразование треугольника сопротивлений в звезду и обратно
сопротивление луча звезды
сопротивление стороны треугольника равно сумме сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.
Слайд 13
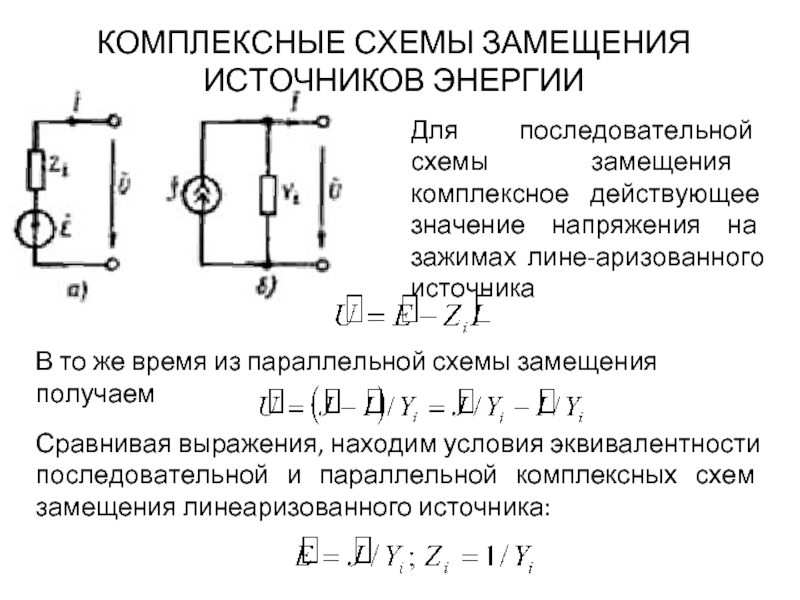
Для последовательной схемы замещения комплексное действующее значение напряжения на зажимах линеаризованного
В то же время из параллельной схемы замещения получаем
Сравнивая выражения, находим условия эквивалентности последовательной и параллельной комплексных схем замещения линеаризованного источника:
КОМПЛЕКСНЫЕ СХЕМЫ ЗАМЕЩЕНИЯ ИСТОЧНИКОВ ЭНЕРГИИ
Слайд 15
КОМПЛЕКСНЫЕ СХЕМЫ ЗАМЕЩЕНИЯ ИСТОЧНИКОВ ЭНЕРГИИ
Идеальные источники тока и напряжения, которые могут
Если в анализируемую цепь включены идеальный источник напряжения и последовательно с ним не введены элементы, сопротивление которых можно рассматривать как внутреннее сопротивление линеаризованного источника, или идеальный источник тока, параллельно которому не включены ветви проводимость которых можно трактовать как внутреннюю проводимость соответствующего источника, то такие источники называют вырожденными.
Слайд 18
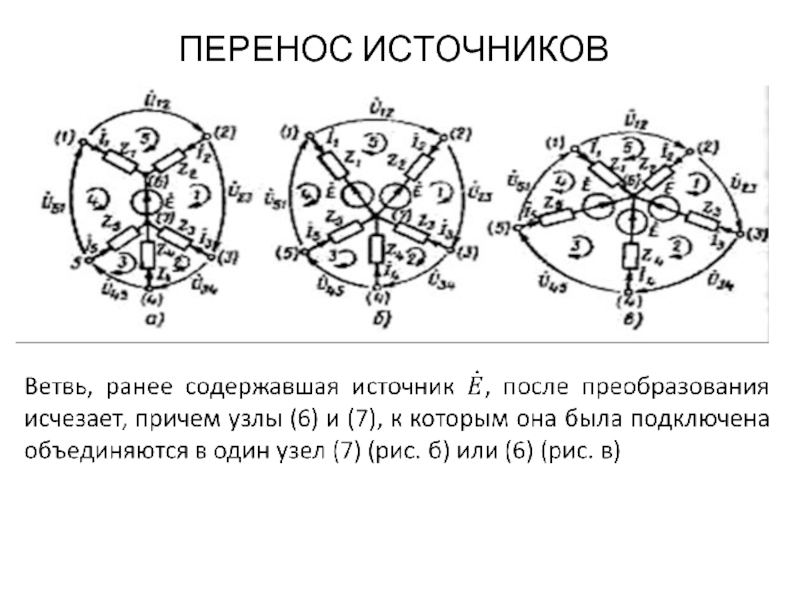
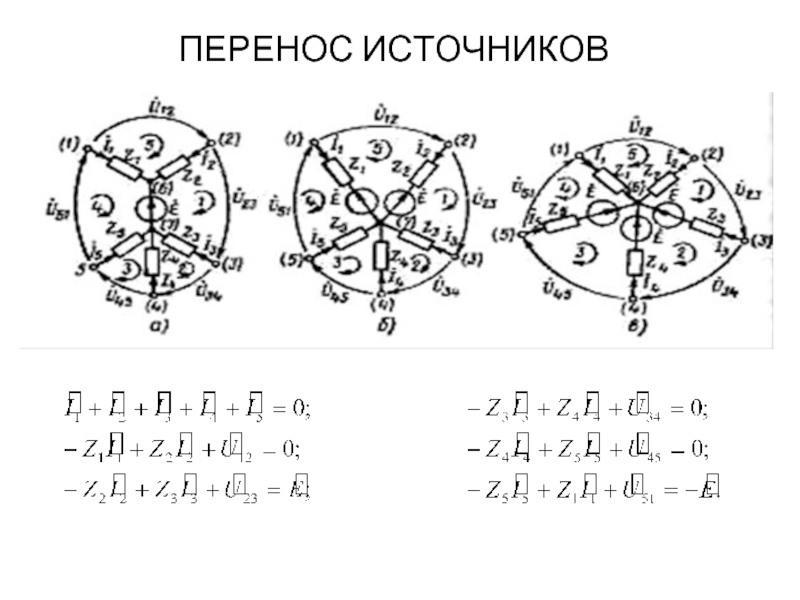
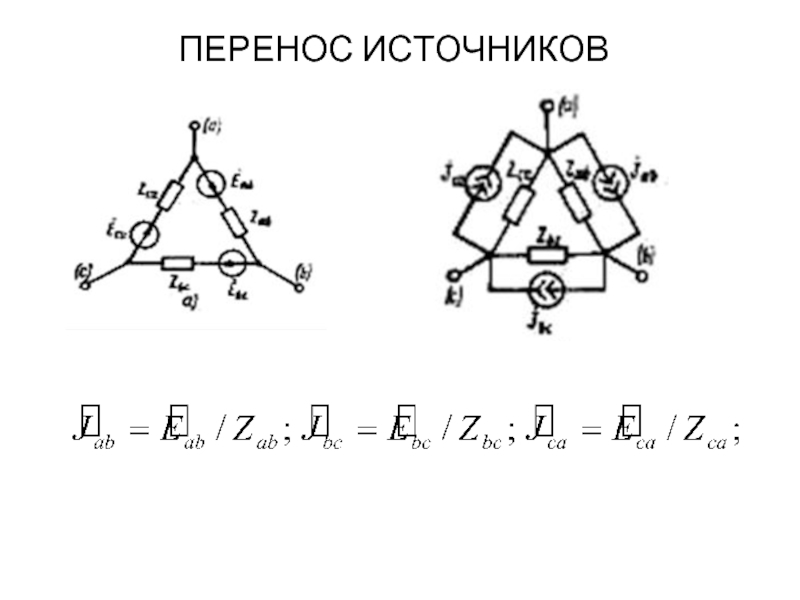
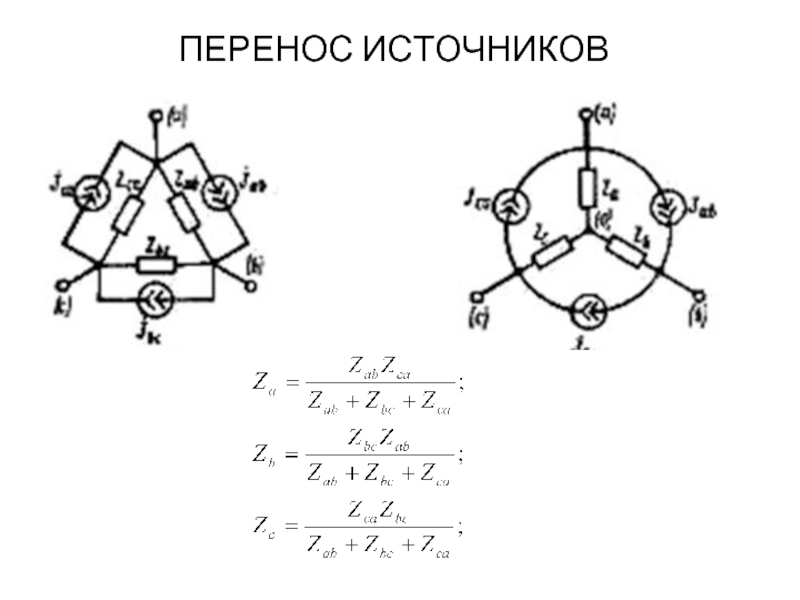
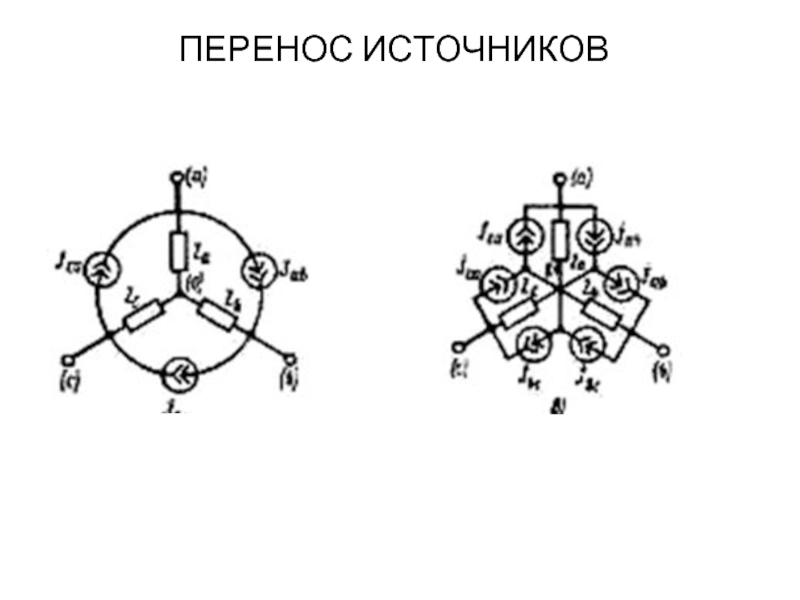
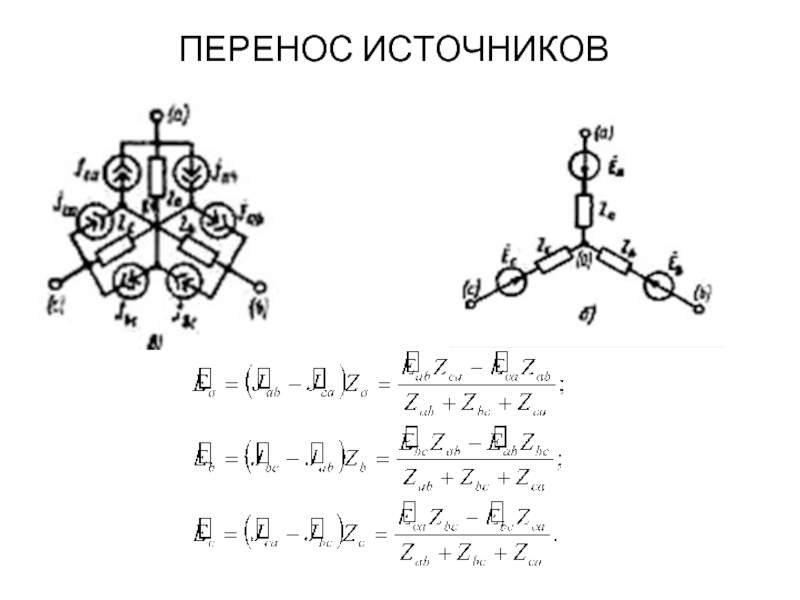
ПЕРЕНОС ИСТОЧНИКОВ
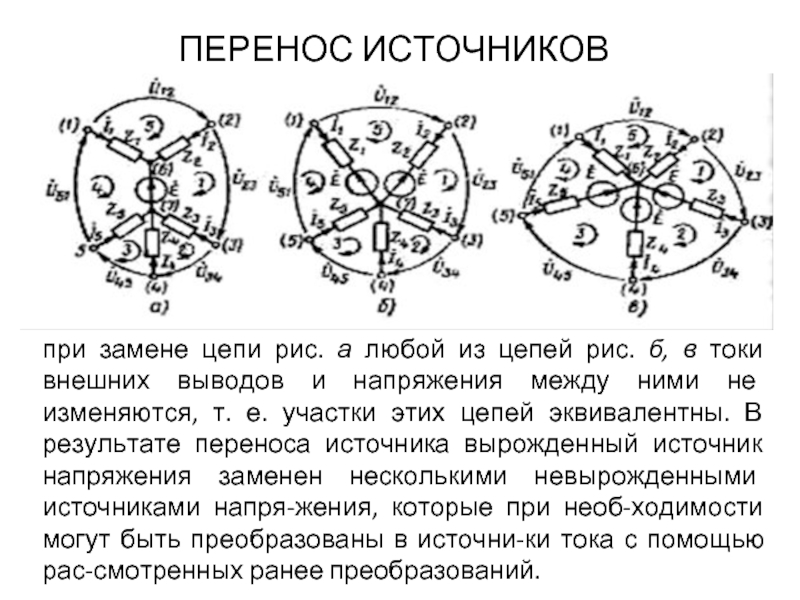
при замене цепи рис. а любой из цепей рис. б,
Слайд 19
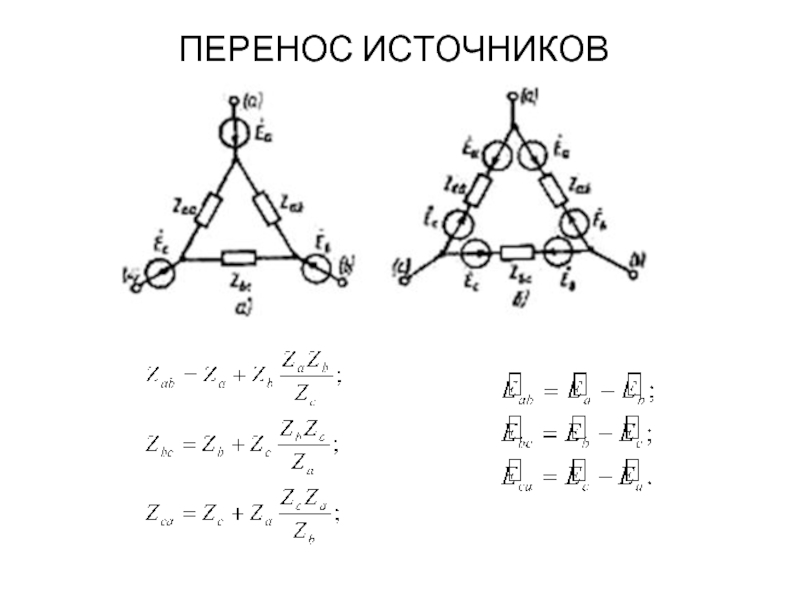
ПЕРЕНОС ИСТОЧНИКОВ
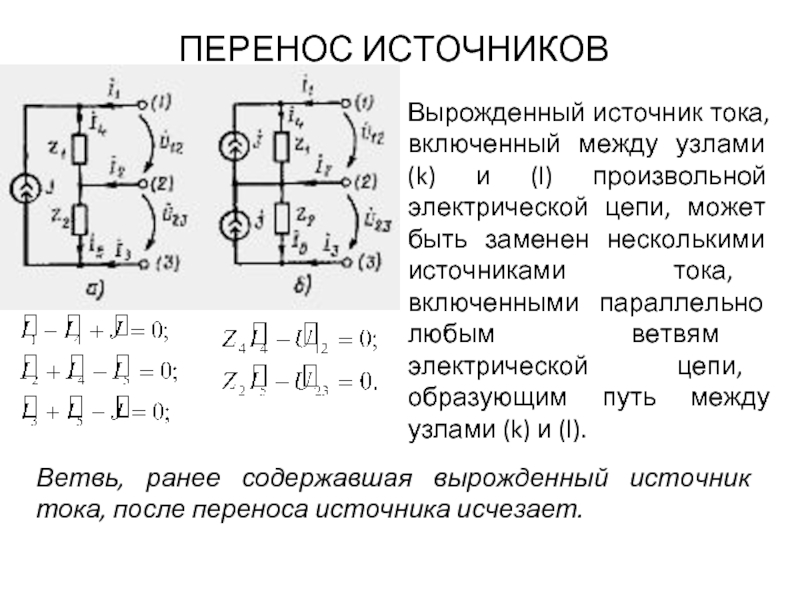
Вырожденный источник тока, включенный между узлами (k) и (l) произвольной
Ветвь, ранее содержавшая вырожденный источник тока, после переноса источника исчезает.