- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Плоское потенциальное движение. Использование вихревой теории в расчетах турбомашин презентация
Содержание
- 1. Плоское потенциальное движение. Использование вихревой теории в расчетах турбомашин
- 2. Лекция 11 Плоское потенциальное движение
- 3. Следовательно, можно считать, что поток имеет равные
- 4. Использование вихревой теории в расчетах турбомашин Таким
- 5. Относительный поток в каналах колеса не только
- 6. Использование вихревой теории в расчетах турбомашин При
- 7. Использование вихревой теории в расчетах турбомашин За
- 8. Использование вихревой теории в расчетах турбомашин Было
- 9. Использование вихревой теории в расчетах турбомашин Его
- 10. Использование вихревой теории в расчетах турбомашин При
- 11. Использование вихревой теории в расчетах турбомашин Очевидно,
- 12. Теорема Жуковского для решетки профилей Теорема
- 13. Такие вихри, определяющие величину подъемной силы, Жуковский
- 14. Если мы рассечем все лопатки колеса осевой
- 15. Теорема Жуковского для решетки профилей Плоская
- 16. Теорема Жуковского для решетки профилей Пусть
- 17. Запишем уравнение в проекциях на оси координат
- 18. ось у Теорема Жуковского для решетки
- 19. Так как скорость можно выразить через проекции
- 20. Поэтому в результате циркуляция будет выражена обходом
- 21. Теорема Жуковского для решетки профилей Fпоту=t
- 22. Вернемся к рисунку и совместим прямоугольники скоростей Теорема Жуковского для решетки профилей
- 23. Теорема Жуковского для решетки профилей Из
- 24. Теорема Жуковского для решетки профилей Однако
- 25. Теорема Жуковского для решетки профилей Fпоту
- 26. В соответствии с возникновением силы лобового соп-ротивления
- 27. Теорема Жуковского для решетки профилей Также
- 28. Анализ работы турбомашины по вихревой теории Лопатка
- 29. Анализ работы турбомашины по вихревой теории Эти
- 30. Если эти величины определять по окружности ради-
- 31. Анализ работы турбомашины по вихревой теории можно
- 32. Анализ работы турбомашины по вихревой теории Тогда
- 33. ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ Турбомашины обладают тем
- 34. ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ У центробежных машин
- 35. ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ с2r Тогда теоретическая
- 36. ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ Чтобы выразить скорость
- 37. ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ Подставляя это
- 38. ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ Уравнение содержит переменные
Слайд 3Следовательно, можно считать, что поток имеет равные скоро-сти и давления во
Использование вихревой теории в расчетах турбомашин
Однако в действительности при конечном числе лопаток давление с передней (лобовой) стороны лопатки должно быть выше, чем с задней стороны, причем именно благодаря этой разности давлений турбомашина может, сообщать жидкости энергию.
Слайд 4Использование вихревой теории в расчетах турбомашин
Таким образом, неточность струйной теории заклю-чается
Рабочее колесо передает жидкости некоторый вра-щательный момент, и на отдельных элементах ло-патки имеют место разности давлений. Это создает различные по величине относительные скорости в канале между лопатками.
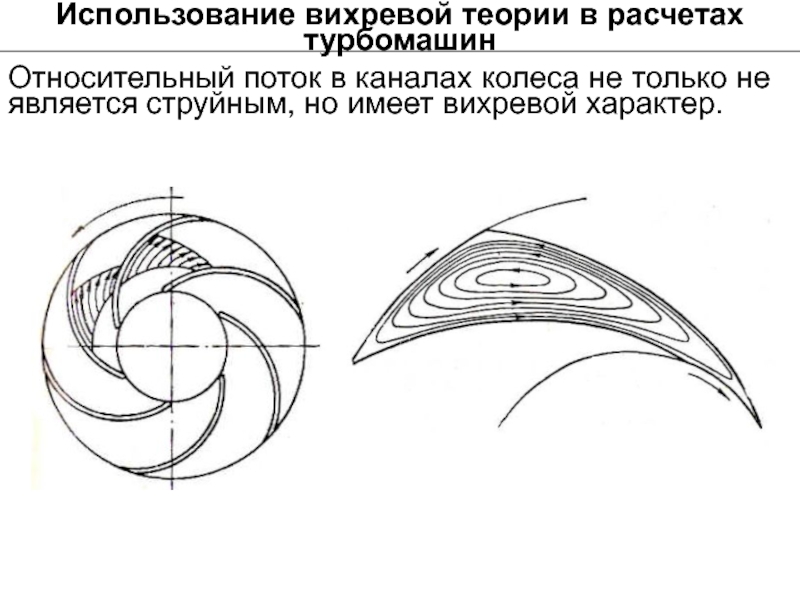
Слайд 5Относительный поток в каналах колеса не только не является струйным, но
Использование вихревой теории в расчетах турбомашин
Слайд 6Использование вихревой теории в расчетах турбомашин
При обтекании тела потоком возникают силы
Рассмотрим обтекание плоской пластинки потоком при движении ее под углом 90° к потоку.
Струя а, направленная нa центр пластинки, по мере приближения к пластинке теpяет свою скорость
При этом по закону Бернулли увеличивается давление потока. Соседние струи увеличенным давлением оттесняются к краям пластинки, где происходит сужение потока, скорости возрастают и давление падает. Таким образом, наибольшее давление поток производит в точке 1 и наименьшее – в точке 4.
Слайд 7Использование вихревой теории в расчетах турбомашин
За пластинкой жидкость, стремясь заполнить область
Чем больше вихреобразование, тем сильнее разре-жение. Плоская пластинка является плохо обтека-емой формой.
Возникшая разность давлений создает силу, направ-ленную в сторону, обратную движению пластинки. Эта сила называется силой сопротивления.
Из теоремы импульсов получается формула, по ко-торой определяется величина силы сопротивления:
С – коэффициент, зависящий от формы тела
Слайд 8Использование вихревой теории в расчетах турбомашин
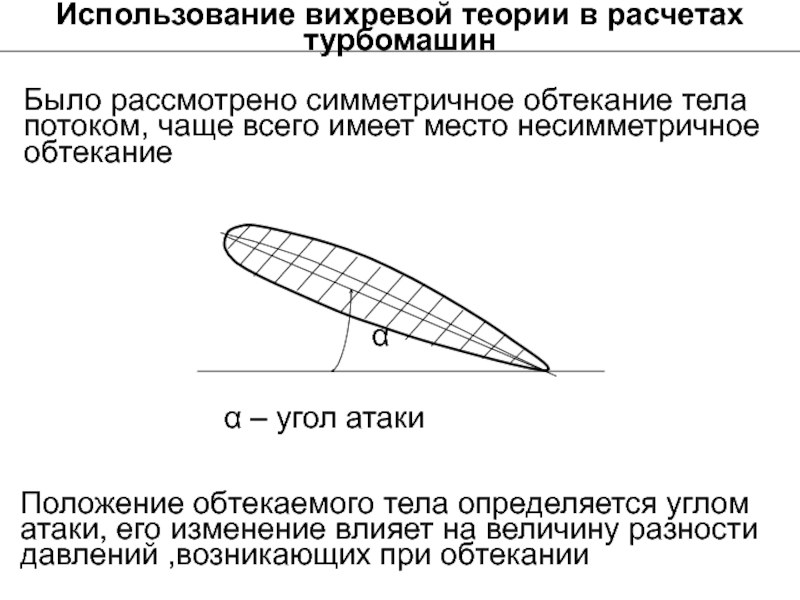
Было рассмотрено симметричное обтекание тела потоком,
α
α – угол атаки
Положение обтекаемого тела определяется углом атаки, его изменение влияет на величину разности давлений ,возникающих при обтекании
Слайд 9Использование вихревой теории в расчетах турбомашин
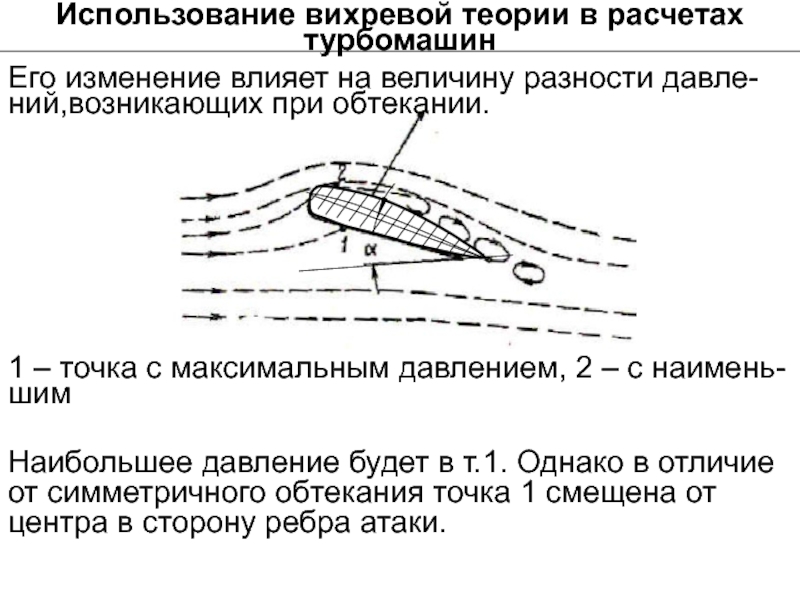
Его изменение влияет на величину разности
Наибольшее давление будет в т.1. Однако в отличие от симметричного обтекания точка 1 смещена от центра в сторону ребра атаки.
1 – точка с максимальным давлением, 2 – с наимень-шим
Слайд 10Использование вихревой теории в расчетах турбомашин
При обтекании верхней части профиля, вследствие
Ниже точки 2 имеет место вихреобразование, вызы-ваемое трением потока о поверхность.
Слайд 11Использование вихревой теории в расчетах турбомашин
Очевидно, что в основном все элементы,
Сα – коэффициент, зависящий от формы тела и угла атаки
Слайд 12 Теорема Жуковского для решетки профилей
Теорема Жуковского была опубликована в 1906
Теорема получила также широкое применение в теории гребных винтов кораблей, теории лопастных гидравлических и газовых турбомашин.
Ее значение определяется тем, что она вскрывает физическую причину появления подъемной силы, при которой являются вихри. Мерой интенсивности последних является циркуляция скорости.
При этом несущественна причина, порождающая вих-ри. Для идеальной жидкости циркуляция обусловлена течением плоского вихря.
Слайд 13Такие вихри, определяющие величину подъемной силы, Жуковский называл присоединенными.
В реальной жидкости
Теорема Жуковского для решетки профилей
Окончательно вопрос о расчете величины подъемной силы решил постулат Чаплыгина-Жуковского, устра-нивший неопределенность величины циркуляции для крыловых профилей.
Слайд 14Если мы рассечем все лопатки колеса осевой турбо-машины двумя цилиндрическими поверхностями,
Бесконечная совокупность одинаковых крыловых профилей, одинаково ориентированных и расположенных с постоянным шагом вдоль прямой, называется плоской гидродинамической решет-кой.
Теорема Жуковского для решетки профилей
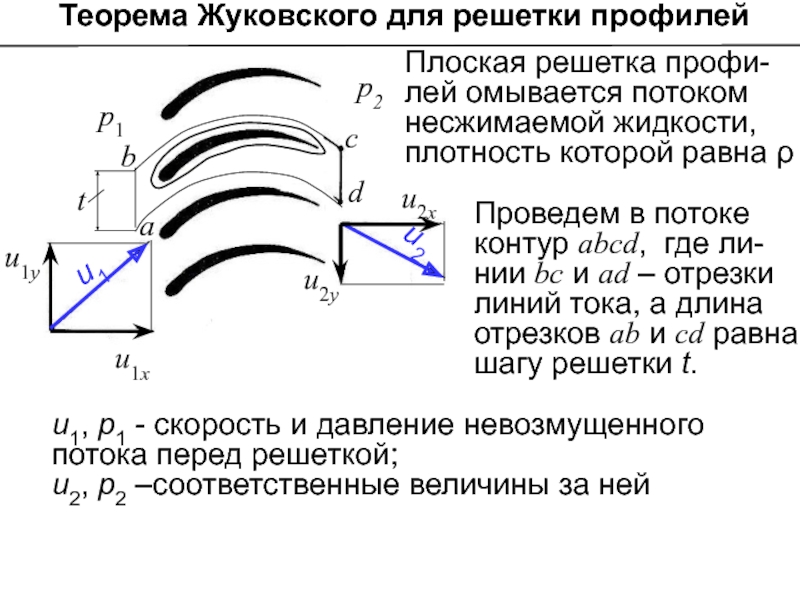
Слайд 15 Теорема Жуковского для решетки профилей
Плоская решетка профи-лей омывается потоком несжимаемой
Проведем в потоке контур abcd, где ли-нии bc и ad – отрезки линий тока, а длина отрезков ab и cd равна шaгy решетки t.
и1, р1 - скорость и давление невозмущенного потока перед решеткой;
и2, р2 –соответственные величины за ней
Слайд 16 Теорема Жуковского для решетки профилей
Пусть поток перед решеткой и за
Тогда из условия постоянства расхода жидкости Q через решетку, его величину
Q=u1xt= u2xt
Напишем для контура abcd уравнение количества движения
Масса в единицу времени определится как массовый расход: m= ρQ= ρuхt , тогда
Так как течение плоское, расчеты ведутся для единицы ширины профиля
откуда
u1x= u2x= ux
Слайд 17Запишем уравнение в проекциях на оси координат
Теорема Жуковского для решетки
Fпр-- сила, действующая со стороны профиля на поток; Fпот – сила, c которой поток действует на профиль. Они равны по величине и противоположно направлены.
R - силы давления; силы давления, приложенные к отрезкам bc и ad, считаем равными по величине и противоположно направленными, т. е. их действие уравновешено.
ось х
t(ρuх2 –ρuх2)= р1t – р2t -Fпотх
t(ρuх2 –ρuх2)= t (р1 – р2) -Fпотх
0
Fпотх= t (р1 – р2)
Слайд 18ось у
Теорема Жуковского для решетки профилей
t(ρuхu2у –ρuх u1у)= -Fпоту
t ρuх(u2у
Fпоту=t ρuх(u1у –u2у)
Fпотх= t (р1 – р2)
Выразим разность давлений из уравнения Бернулли для идеальной жидкости
Слайд 19Так как скорость можно выразить через проекции
то уравнение можно представить в
Теорема Жуковского для решетки профилей
Обратимся к циркуляции по замкнутому контуру abcd. При этом части контурного интеграла, соответствую-щие обходу участков линий тока bc и da взаимно уничтожаются, так как значения скоростей в соответ-ственных точках этих участков одинаковы, а направ-ления обхода противоположны.
Слайд 20Поэтому в результате циркуляция будет выражена обходом по частям ab и
Заменим одну скобку в формуле циркуляцией
Теорема Жуковского для решетки профилей
Учитывая полученное соотношение, подставим это в выражение для горизонтальной проекции силы, с которой поток воздействует на профиль решетки
Fпотх= t (р1 – р2)
Слайд 21 Теорема Жуковского для решетки профилей
Fпоту=t ρuх(u1у –u2у)
Вертикальная составляющая силы будет
Результирующая сила
Рассмотрим множитель, представленный в виде корня
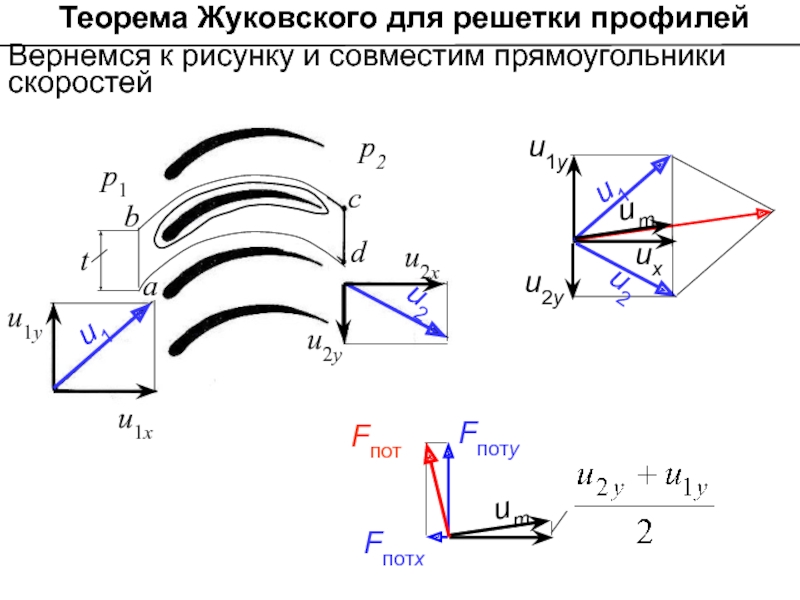
Слайд 22Вернемся к рисунку и совместим прямоугольники скоростей
Теорема Жуковского для решетки
Слайд 23 Теорема Жуковского для решетки профилей
Из сложения скоростей видно, что скорость
Тогда
Формула выражает теорему Жуковского для профиля в плоской решетке.
Слайд 24 Теорема Жуковского для решетки профилей
Однако наличия только такой связи недостаточно
Это условие формулируется так: при безотрывном обтекании профиля вокруг него возникает циркуля-ция Г такой величины, при которой задняя острая кромка является точкой схода струй.
Слайд 25 Теорема Жуковского для решетки профилей
Fпоту
Fпот
Fпотх
Результирующую силу можно разложить на состав-ляющие
Fсопр
Слайд 26В соответствии с возникновением силы лобового соп-ротивления при обтекании тел ,
Теорема Жуковского для решетки профилей
- площадь, равная произведению размаха крыла l на хорду профиля b;
Сх- коэффициент лобового сопротивления.
Слайд 27 Теорема Жуковского для решетки профилей
Также и подъемную силу можно выразить
Су- коэффициент подъемной силы.
Коэффициенты Сх и Су определяют эксперимен-тально.
Слайд 28Анализ работы турбомашины по вихревой теории
Лопатка рабочего колеса турбомашины представля-
ет собой
Акад. Г. Ф. Проскура на основе вихревой теории кры-
ла проф. Н. Е. Жуковского создал вихревую теорию турбомашин
Рабочий процесс в турбомашине по этой теории про-текает следующим образом: при вращении ротора турбомашины за счет динамического воздействия на жидкость лопаток колеса, обтекаемых потоком, появ-ляются гидроаэродинамические силы, создающие приращение полного напора, необходимого для пере-мещения потока во внешней сети турбоустановки.
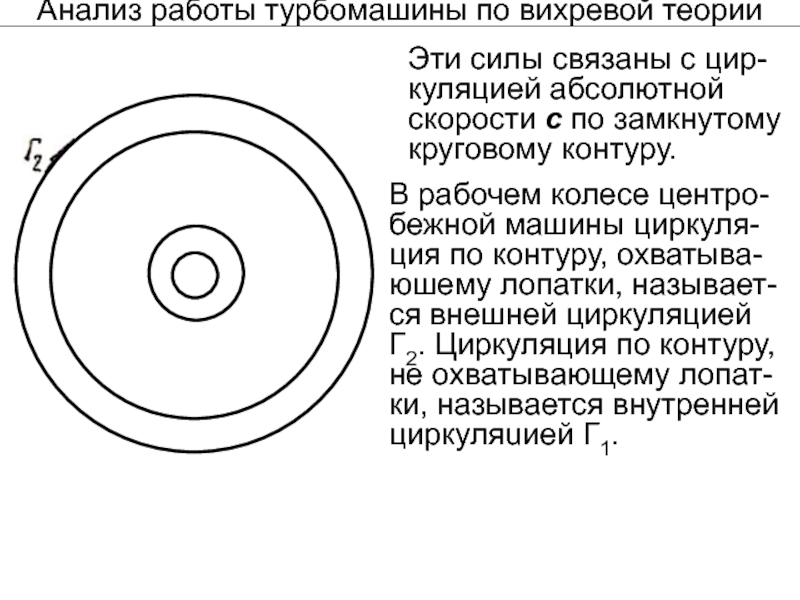
Слайд 29Анализ работы турбомашины по вихревой теории
Эти силы связаны с цир-куляцией абсолютной
В рабочем колесе центро-
бежной машины циркуля-
ция по контуру, охватыва-
юшему лопатки, называет-
ся внешней циркуляцией Г2. Циркуляция по контуру, не охватывающему лопат-
ки, называется внутренней циркуляuией Г1.
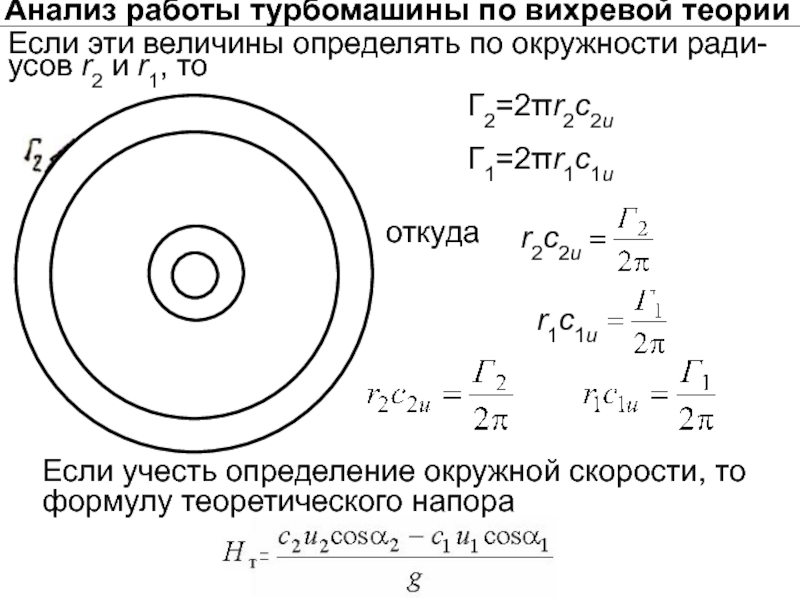
Слайд 30Если эти величины определять по окружности ради-
усов r2 и r1, то
Анализ
Г2=2πr2с2и
Г1=2πr1с1и
откуда
Если учесть определение окружной скорости, то формулу теоретического напора
Слайд 31Анализ работы турбомашины по вихревой теории
можно выразить
Так как внешняя и внутренняя
Таким образом, наличие циркуляции в каналах между лопатками вытекает из существа вихревой теории. Это же явление наблюдается и на опытах.
Циркуляция по какому-либо контуру равняется сумме циркуляций по замкнутым линиям, заключенным внутри рассматриваемого контура.
Г2=Г1+zГs
Г2-Г1=zГs
Слайд 32Анализ работы турбомашины по вихревой теории
Тогда
Вихревая теория не включает для турбомашин
Слайд 33ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
Турбомашины обладают тем свойством, что их пода-ча, давление,
Количество жидкости, которое пройдет через рабо-чее колесо турбомашины в единицу времени, т. е. его подачу, можно определить, пользуясь уравнени-ем расхода:
Q=ωc,
где ω- площадь живого сечения потока, м2;
с - средняя скорость жидкости, нормальная к этому сечению, м/сек.
Слайд 34ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
У центробежных машин площадь выходного живого сечения рабочего
ω = πD2b2.
Средней скоростью, нормальной к этой поверхности, будет проекция абсолютной скорости с2 на направ-ление радиуса, т. е.
с2r = с2sinα2
Скорость с2r называется радиальной или меридио-нальной.
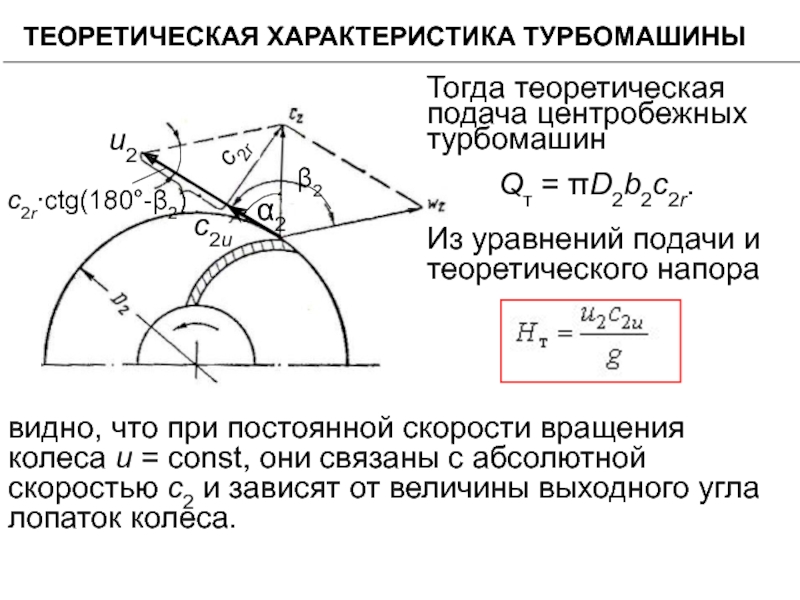
Слайд 35ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
с2r
Тогда теоретическая подача центробежных турбомашин
Qт = πD2b2с2r.
видно, что
Из уравнений подачи и теоретического напора
Слайд 36ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
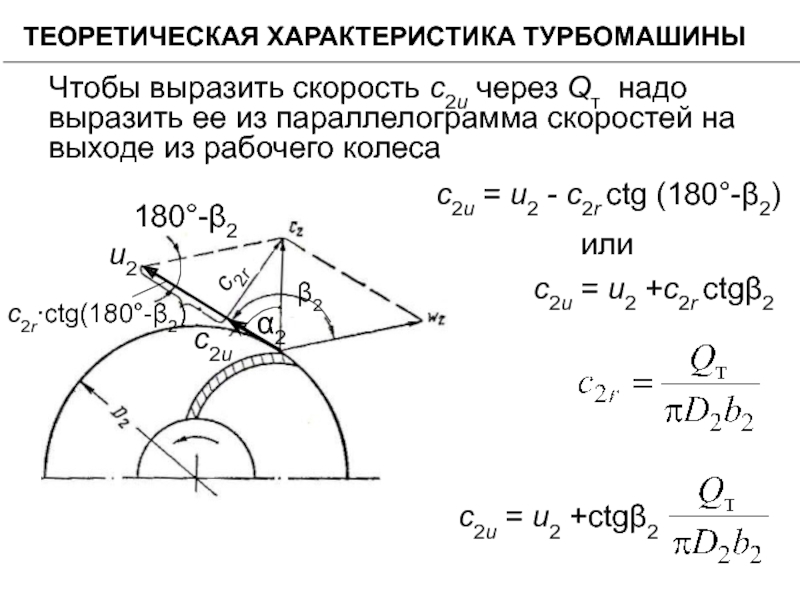
Чтобы выразить скорость с2и через Qт надо выразить
с2и = и2 - с2r ctg (180°-β2)
или
с2и = и2 +с2r ctgβ2
180°-β2
с2r
Слайд 37ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА ТУРБОМАШИНЫ
Подставляя это значение в формулу теоретического напора, получим
Уравнение выражает зависимость давления от подачи для одноколесной турбомашины.