Дифференциальные уравнения движения презентация

Содержание

1. Дифференциальные уравнения движения
2. - основной закон динамики Дифференциальные уравнения движения
3. - векторная форма задания движения - координатный способ задания движения - в естественных координатах
4. § 1. Прямолинейное движение сила (или равнодействующая
5. если сила (или равнодействующая сил) зависит от
6. Решение основной задачи динамики – нахождение
7. § 2. Схема решения дифференциальных уравнений движения
8. § 3. Примеры Задача 1 Груз веса
9. Задача 1 P =
10. Начальные условия: t = 0, x
11. - общее решение - частное
12. Задача 2 К твердому телу
13. Задача 2 M =1 кг,
14. - общее решение - закон
15. Задача 3 Лодку с пассажиром,
16. Задача 3 m=120 кг,
17. Начальные условия: t = 0,
18. - общее решение - закон изменения
19. Задача 4 Камень массы m,
20. Задача 4 m, V0,
21. x: разделяем переменные интегрируем ? y: - общие решение дифференциальных уравнений
22. Начальные условия: t
23. Общие решения дифференциальных
24. Горизонтальная дальность полета: - расстояние ОС Высота полета:
25. Время
26. Задача 5 Парашютист в момент
27. Задача 5 m, V0,
28. - общее решение - частное
29. - закон изменения скорости Ответ. Скорость парашютиста изменяется согласно полученному закону

- основной закон динамики Дифференциальные уравнения движения

Главная
Физика
Дифференциальные уравнения движения

Слайд 1Глава 1
Дифференциальные уравнения движения
§ 1. Прямолинейное движение
§ 2. Схема решения

дифференциальных уравнений движения
§ 3. Примеры решения задач

Слайд 2- основной закон динамики
Дифференциальные уравнения движения

Слайд 3- векторная форма задания движения
- координатный способ задания движения
- в естественных

координатах

Слайд 4§ 1. Прямолинейное движение
сила (или равнодействующая сил) имеет постоянное направление
скорость точки

в начальный момент времени направлена вдоль силы или равна нулю

или

то

т.к.

Слайд 5если сила (или равнодействующая сил) зависит от координаты x, а не

от времени t
или
по условию задачи надо найти зависимость скорости Vx от координаты x, то

тогда

Слайд 6Решение основной задачи динамики – нахождение x = f(t)
Cила (равнодействующая сил)

может зависеть от времени t, положения x и скорости точки vх

- общее решение уравнения,

Дважды интегрируя это уравнение, находим

- частное решение уравнения

Слайд 7§ 2. Схема решения дифференциальных уравнений движения
Составить дифференциальное уравнение:
-

выбрать систему координат и начало отсчета;
- изобразить тело в произвольный момент времени и все действующие на него силы;
- найти суммы проекций всех сил на оси координат
Интегрирование дифференциальных уравнений
Нахождение постоянных интегрирования
Определение искомых величин и исследование полученных результатов

Слайд 8§ 3. Примеры
Задача 1
Груз веса Р, находившийся в покое на гладкой

горизонтальной поверхности, начинает двигаться под действием горизонтальной силы, проекция которой на горизонталь равна Fx = H sin(kt), где H и k – постоянные величины. Найти закон движения

Слайд 9
Задача 1
P = mg,
Fx= H sin(kt),
t=0, x=0, Vx=0
x(t) -

- общее решение дифференциального уравнения

Слайд 10
Начальные условия: t = 0, x = 0, Vx = 0
-

частное решение дифф. уравнения

- еще одно дифф. уравнение

Слайд 11

- общее решение
- частное решение дифф. уравнения
- решение задачи
Начальные условия: t

= 0, x = 0, Vx = 0

Вывод. На равномерное движение груза со скоростью V = H / (k · m), происходящее по горизонтали вправо, накладывается колебание с амплитудой A = H / (k2· m) и периодом – T = 2·π / k

Слайд 12 Задача 2
К твердому телу массы m =1 кг, которое

может двигаться вдоль оси x, приложена сила притяжения, проекция которой на ось x направлена по горизонтали налево и равна Sx = 2 x. Тело двигалось с начальной скоростью V0 = 10 м/с вправо. Определить скорость тела, когда оно пройдет путь 5 м

Слайд 13 Задача 2
M =1 кг, Sx= 2 x,
t = 0,

x0 = 0,
V0=10 м/c, xk= 5 м

Vk - ?

Слайд 14

- общее решение
- закон изменения скорости
Начальные условия: t = 0, x

= 0, Vx = 10 м/с

Ответ. Скорость тела, когда оно пройдет путь 5 м, будет 7.07 м/с

Слайд 15 Задача 3
Лодку с пассажиром, масса которых m = 120

кг, толкают, сообщая начальную скорость V0 = 2 м/с. Считать силу сопротивления воды при малых скоростях изменяющейся по закону R = µV, где µ = 9.1 кг/с. Найти путь, который пройдет лодка до остановки

Слайд 16
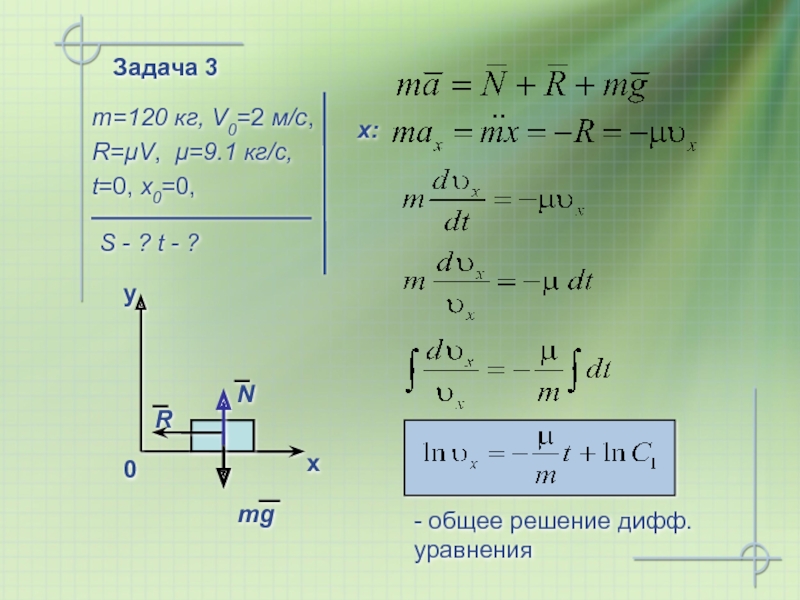
Задача 3
m=120 кг, V0=2 м/c,
R=µV, µ=9.1 кг/с,
t=0, x0=0,

S - ? t - ?

- общее решение дифф. уравнения

Слайд 17

Начальные условия: t = 0, x = 0, Vx = 2

м/с

- частное решение дифф. уравнения

- еще одно дифф. уравнение

Слайд 18- общее решение

- закон изменения скорости
Начальные условия: t = 0, x

= 0, Vx = 2 м/с

Ответ. Лодка будет двигаться очень долго и будет стремиться преодолеть путь около 26.6 м

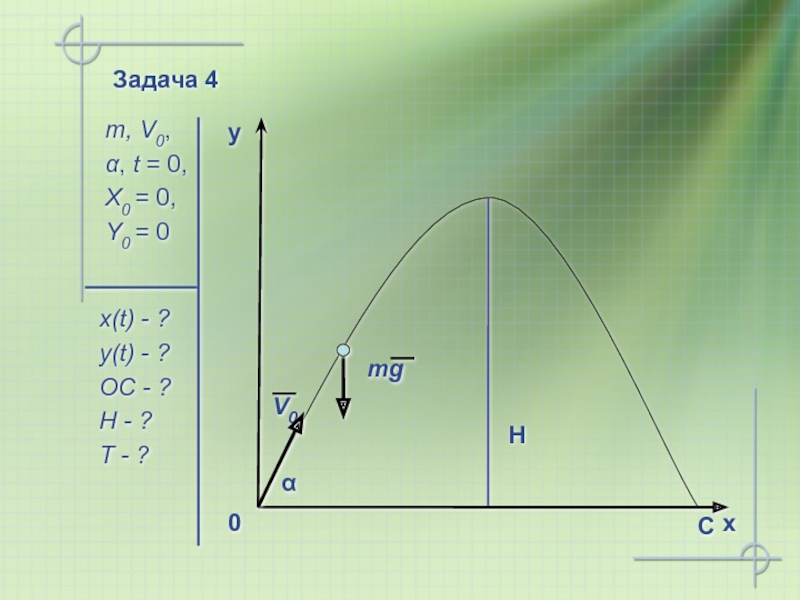
Слайд 19 Задача 4
Камень массы m, брошен под углом α

к горизонтальной плоскости со скоростью V0. Определить траекторию движения, горизонтальную дальность полета, высоту полета и время полета камня. Сопротивлением воздуха пренебречь

Слайд 20
Задача 4
m, V0,
α, t = 0,
X0 =

0,
Y0 = 0

x(t) - ?
y(t) - ?
OC - ?
H - ?
T - ?

Слайд 21

x:

разделяем переменные
интегрируем
?
y:
- общие решение дифференциальных уравнений

Слайд 22

Начальные условия: t = 0, Vx = V0 cosα,

Vy = V0 sinα

- частные решения дифференциальных уравнений

- еще два дифференциальных уравнения

Слайд 23

Общие решения дифференциальных уравнений
- частные решения дифференциальных уравнений
Траектория движения камня:

Уравнение параболы с осью параллельной оси OY

Брошенное под углом к горизонту тело движется в безвоздушном пространстве по параболе (Г. Галилей)

Слайд 24 Горизонтальная дальность полета:

- расстояние ОС
Высота полета:

Слайд 25

Время полета:
расстояние ОС будет одинаковым для обоих случаев

Угол наибольшей дальности:

При α = 45О Х будет максимальным

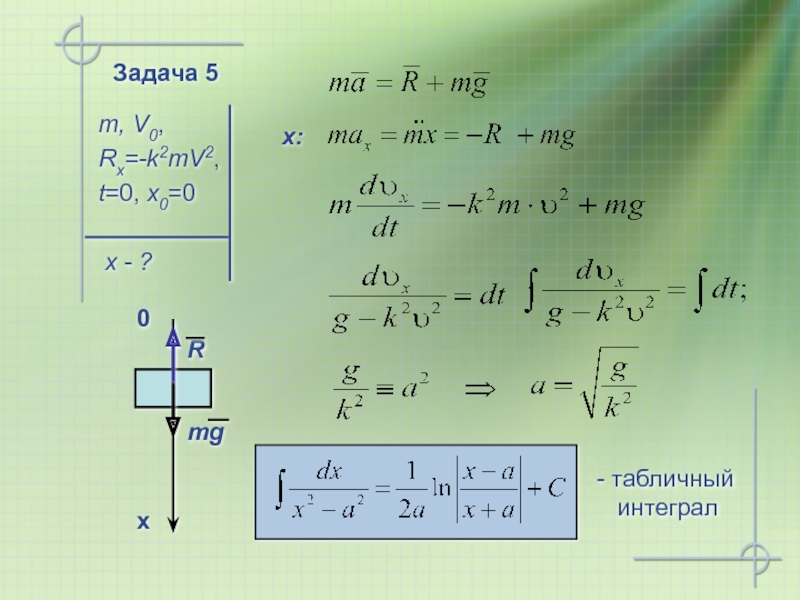
Слайд 26 Задача 5
Парашютист в момент раскрытия парашюта имел скорость V0,

направленную вертикально вниз. Найти скорость парашютиста, если проекция силы сопротивления движению на вертикаль Rх = –k2mV2, где m – масса парашютиста; k – постоянный коэффициент; V – скорость в проекции на вертикаль

Слайд 27 Задача 5
m, V0,
Rх=-k2mV2,
t=0, x0=0

x - ?
x
0

x:

-

табличный интеграл

Слайд 28

- общее решение
- частное решение
Начальные условия: t = 0, x =

потенцируем это уравнение и получим

Слайд 29
- закон изменения скорости
Ответ. Скорость парашютиста изменяется согласно полученному

закону

Скачать презентацию

Дифференциальные уравнения движения презентация

Содержание

Слайд 1Глава 1
Дифференциальные уравнения движения
§ 1. Прямолинейное движение
§ 2. Схема решения

Слайд 2- основной закон динамики
Дифференциальные уравнения движения

Слайд 3- векторная форма задания движения
- координатный способ задания движения
- в естественных

Слайд 4§ 1. Прямолинейное движение
сила (или равнодействующая сил) имеет постоянное направление
скорость точки

Слайд 5если сила (или равнодействующая сил) зависит от координаты x, а не

Слайд 6Решение основной задачи динамики – нахождение x = f(t)
Cила (равнодействующая сил)

Слайд 7§ 2. Схема решения дифференциальных уравнений движения
Составить дифференциальное уравнение:
-

Слайд 8§ 3. Примеры
Задача 1
Груз веса Р, находившийся в покое на гладкой

Слайд 9
Задача 1
P = mg,
Fx= H sin(kt),
t=0, x=0, Vx=0
x(t) -

Слайд 10
Начальные условия: t = 0, x = 0, Vx = 0
-

Слайд 11

- общее решение
- частное решение дифф. уравнения
- решение задачи
Начальные условия: t

Слайд 12 Задача 2
К твердому телу массы m =1 кг, которое

Слайд 13 Задача 2
M =1 кг, Sx= 2 x,
t = 0,

Слайд 14

- общее решение
- закон изменения скорости
Начальные условия: t = 0, x

Слайд 15 Задача 3
Лодку с пассажиром, масса которых m = 120

Слайд 16
Задача 3
m=120 кг, V0=2 м/c,
R=µV, µ=9.1 кг/с,
t=0, x0=0,

Слайд 17

Начальные условия: t = 0, x = 0, Vx = 2

Слайд 18- общее решение

- закон изменения скорости
Начальные условия: t = 0, x

Слайд 19 Задача 4
Камень массы m, брошен под углом α

Слайд 20
Задача 4
m, V0,
α, t = 0,
X0 =

Слайд 21

x:

разделяем переменные
интегрируем
?
y:
- общие решение дифференциальных уравнений

Слайд 22

Начальные условия: t = 0, Vx = V0 cosα,

Слайд 23

Общие решения дифференциальных уравнений
- частные решения дифференциальных уравнений
Траектория движения камня:

Слайд 24 Горизонтальная дальность полета:

- расстояние ОС
Высота полета:

Слайд 25

Время полета:
расстояние ОС будет одинаковым для обоих случаев

Слайд 26 Задача 5
Парашютист в момент раскрытия парашюта имел скорость V0,

Слайд 27 Задача 5
m, V0,
Rх=-k2mV2,
t=0, x0=0

x - ?
x
0

x:

-

Слайд 28

- общее решение
- частное решение
Начальные условия: t = 0, x =

Слайд 29
- закон изменения скорости
Ответ. Скорость парашютиста изменяется согласно полученному

Обратная связь

Что такое ThePresentation.ru?

Дифференциальные уравнения движения презентация

Содержание

Слайд 1Глава 1Дифференциальные уравнения движения§ 1. Прямолинейное движение § 2. Схема решения

Слайд 2- основной закон динамикиДифференциальные уравнения движения

Слайд 3- векторная форма задания движения- координатный способ задания движения- в естественных

Слайд 4§ 1. Прямолинейное движениесила (или равнодействующая сил) имеет постоянное направлениескорость точки

Слайд 5если сила (или равнодействующая сил) зависит от координаты x, а не

Слайд 6Решение основной задачи динамики – нахождение x = f(t)Cила (равнодействующая сил)

Слайд 7§ 2. Схема решения дифференциальных уравнений движения Составить дифференциальное уравнение: -

Слайд 8§ 3. ПримерыЗадача 1Груз веса Р, находившийся в покое на гладкой

Слайд 9 Задача 1P = mg,Fx= H sin(kt),t=0, x=0, Vx=0x(t) -

Слайд 10Начальные условия: t = 0, x = 0, Vx = 0-

Слайд 11- общее решение- частное решение дифф. уравнения- решение задачиНачальные условия: t

Слайд 12 Задача 2К твердому телу массы m =1 кг, которое

Слайд 13 Задача 2M =1 кг, Sx= 2 x,t = 0,

Слайд 14- общее решение- закон изменения скоростиНачальные условия: t = 0, x

Слайд 15 Задача 3Лодку с пассажиром, масса которых m = 120

Слайд 16 Задача 3m=120 кг, V0=2 м/c, R=µV, µ=9.1 кг/с,t=0, x0=0,

Слайд 17Начальные условия: t = 0, x = 0, Vx = 2

Слайд 18- общее решение- закон изменения скоростиНачальные условия: t = 0, x

Слайд 19 Задача 4Камень массы m, брошен под углом α

Слайд 20 Задача 4m, V0, α, t = 0, X0 =

Слайд 21x: разделяем переменныеинтегрируем?y:- общие решение дифференциальных уравнений

Слайд 22 Начальные условия: t = 0, Vx = V0 cosα,

Слайд 23Общие решения дифференциальных уравнений- частные решения дифференциальных уравненийТраектория движения камня:

Слайд 24 Горизонтальная дальность полета:- расстояние ОСВысота полета:

Слайд 25 Время полета:расстояние ОС будет одинаковым для обоих случаев

Слайд 26 Задача 5Парашютист в момент раскрытия парашюта имел скорость V0,

Слайд 27 Задача 5m, V0, Rх=-k2mV2,t=0, x0=0 x - ? x0x:-

Слайд 28- общее решение- частное решениеНачальные условия: t = 0, x =

Слайд 29- закон изменения скорости Ответ. Скорость парашютиста изменяется согласно полученному

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Глава 1
Дифференциальные уравнения движения
§ 1. Прямолинейное движение
§ 2. Схема решения

Слайд 2- основной закон динамики
Дифференциальные уравнения движения

Слайд 3- векторная форма задания движения
- координатный способ задания движения
- в естественных

Слайд 4§ 1. Прямолинейное движение
сила (или равнодействующая сил) имеет постоянное направление
скорость точки

Слайд 6Решение основной задачи динамики – нахождение x = f(t)
Cила (равнодействующая сил)

Слайд 7§ 2. Схема решения дифференциальных уравнений движения
Составить дифференциальное уравнение:
-

Слайд 8§ 3. Примеры
Задача 1
Груз веса Р, находившийся в покое на гладкой

Слайд 9
Задача 1
P = mg,
Fx= H sin(kt),
t=0, x=0, Vx=0
x(t) -

Слайд 10
Начальные условия: t = 0, x = 0, Vx = 0
-

Слайд 11

- общее решение
- частное решение дифф. уравнения
- решение задачи
Начальные условия: t

Слайд 12 Задача 2
К твердому телу массы m =1 кг, которое

Слайд 13 Задача 2
M =1 кг, Sx= 2 x,
t = 0,

Слайд 14

- общее решение
- закон изменения скорости
Начальные условия: t = 0, x

Слайд 15 Задача 3
Лодку с пассажиром, масса которых m = 120

Слайд 16
Задача 3
m=120 кг, V0=2 м/c,
R=µV, µ=9.1 кг/с,
t=0, x0=0,

Слайд 17

Начальные условия: t = 0, x = 0, Vx = 2

Слайд 18- общее решение

- закон изменения скорости
Начальные условия: t = 0, x

Слайд 19 Задача 4
Камень массы m, брошен под углом α

Слайд 20
Задача 4
m, V0,
α, t = 0,
X0 =

Слайд 21

x:

разделяем переменные
интегрируем
?
y:
- общие решение дифференциальных уравнений

Слайд 22

Начальные условия: t = 0, Vx = V0 cosα,

Слайд 23

Общие решения дифференциальных уравнений
- частные решения дифференциальных уравнений
Траектория движения камня:

Слайд 24 Горизонтальная дальность полета:

- расстояние ОС
Высота полета:

Слайд 25

Время полета:
расстояние ОС будет одинаковым для обоих случаев

Слайд 26 Задача 5
Парашютист в момент раскрытия парашюта имел скорость V0,

Слайд 27 Задача 5
m, V0,
Rх=-k2mV2,
t=0, x0=0

x - ?
x
0

x:

-

Слайд 28

- общее решение
- частное решение
Начальные условия: t = 0, x =

Слайд 29
- закон изменения скорости
Ответ. Скорость парашютиста изменяется согласно полученному