- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Переходные процессы в цепях первого порядка презентация
Содержание
- 1. Переходные процессы в цепях первого порядка
- 2. Переходные процессы В линейной электрической цепи, содержащей
- 3. Законы коммутации Первый закон: в ветви электрической
- 4. Начальные условия Начальными условиями называются те значения
- 5. Начальные условия Начальными условиями называются те значения
- 6. Математическое описание Дифференциальное уравнение, описывающее переходный процесс
- 7. Решение диф. уравнения Решение дифференциального уравнения в
- 8. Классический метод расчета Алгоритм расчета переходных процессов
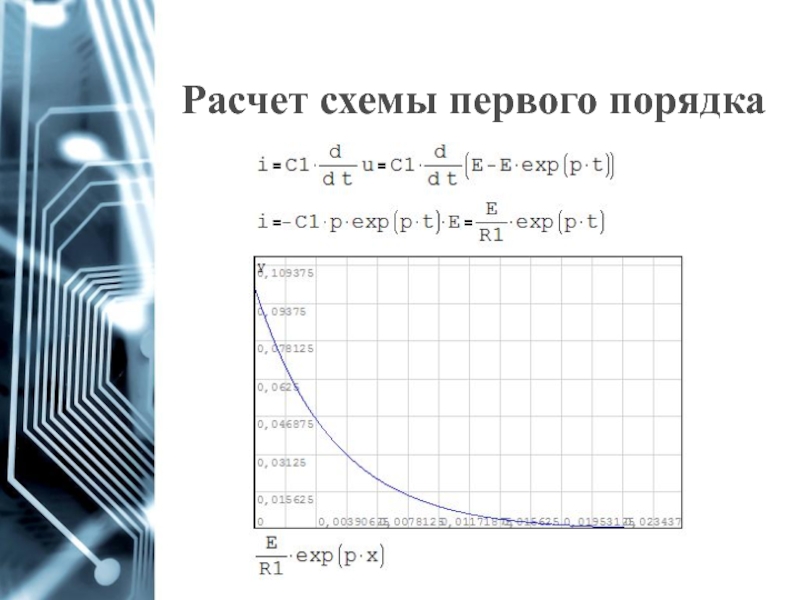
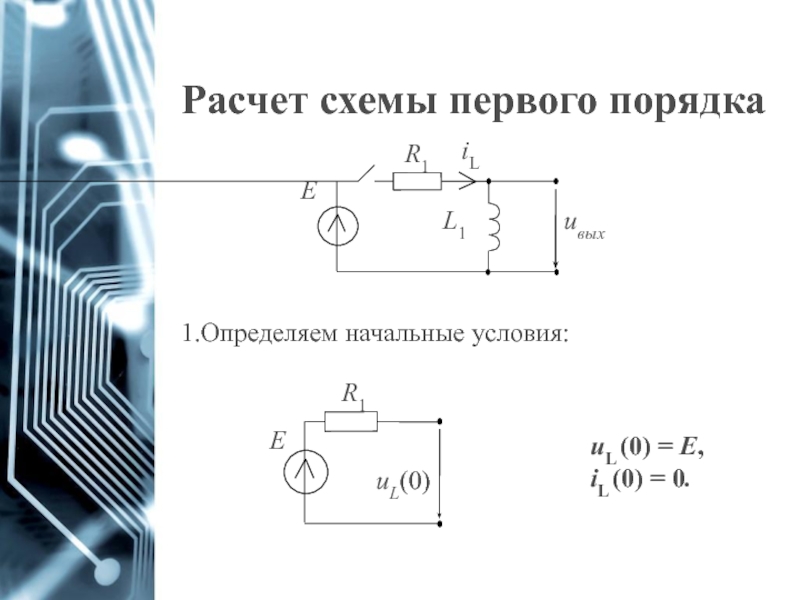
- 9. Расчет схемы первого порядка Определяем начальные
- 10. Расчет схемы первого порядка Найдем
- 11. Расчет схемы первого порядка Составляем
- 12. Расчет схемы первого порядка 4. Определяем
- 13. Расчет схемы первого порядка 5. Записываем
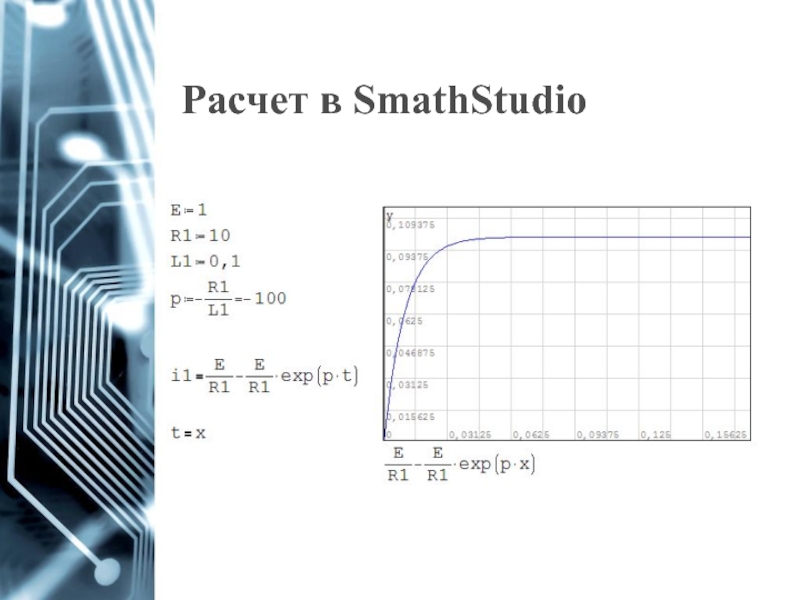
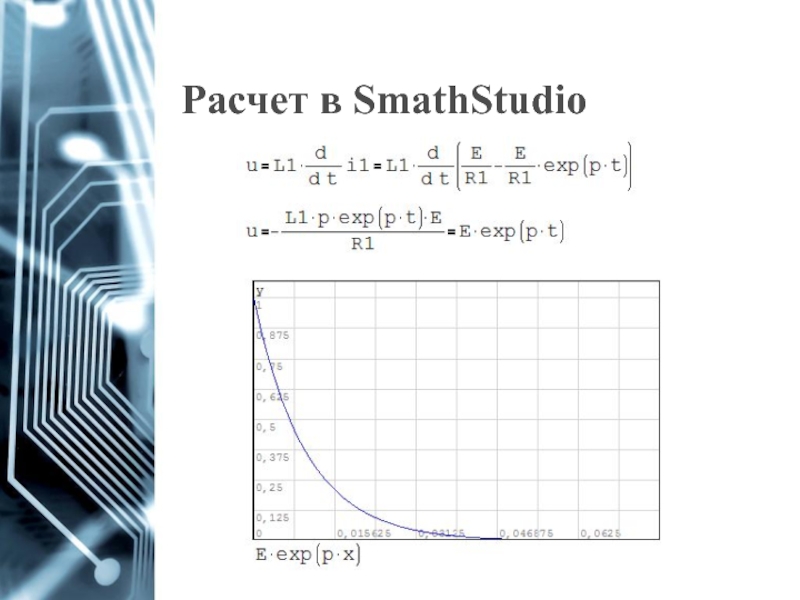
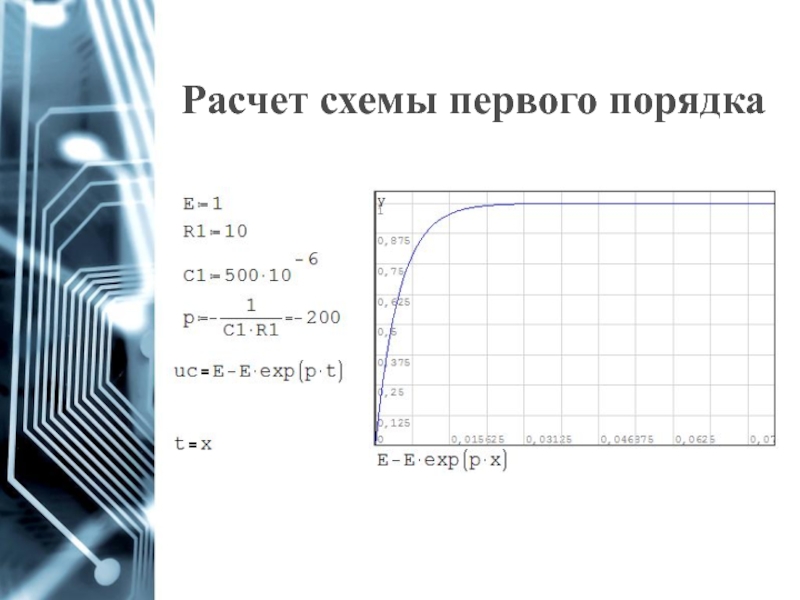
- 14. Расчет в SmathStudio
- 15. Расчет в SmathStudio
- 16. Расчет схемы первого порядка Определяем
- 17. Расчет схемы первого порядка 2.
- 18. Расчет схемы первого порядка 3. Решение
- 19. Расчет схемы первого порядка Составляем
- 20. Расчет схемы первого порядка 4.
- 21. Расчет схемы первого порядка 5. Записываем
- 22. Расчет схемы первого порядка
- 23. Расчет схемы первого порядка
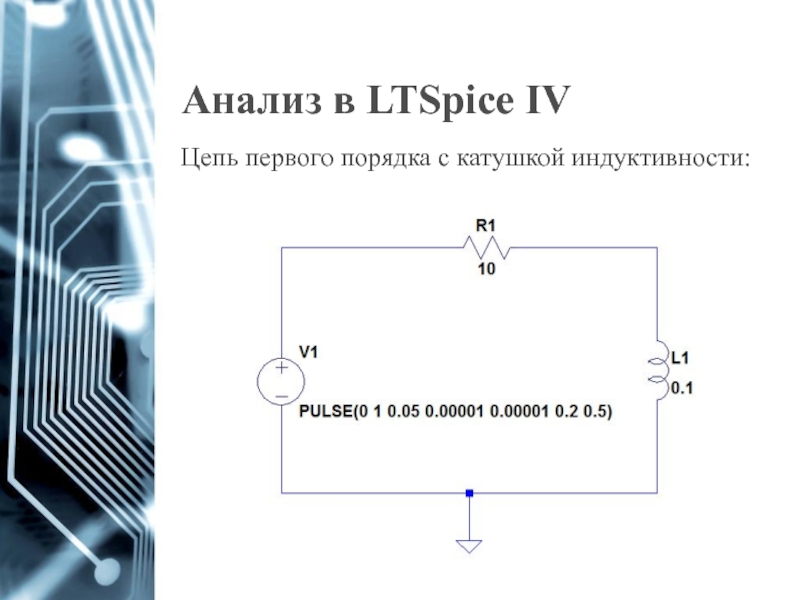
- 24. Анализ в LTSpice IV Цепь первого порядка с катушкой индуктивности:
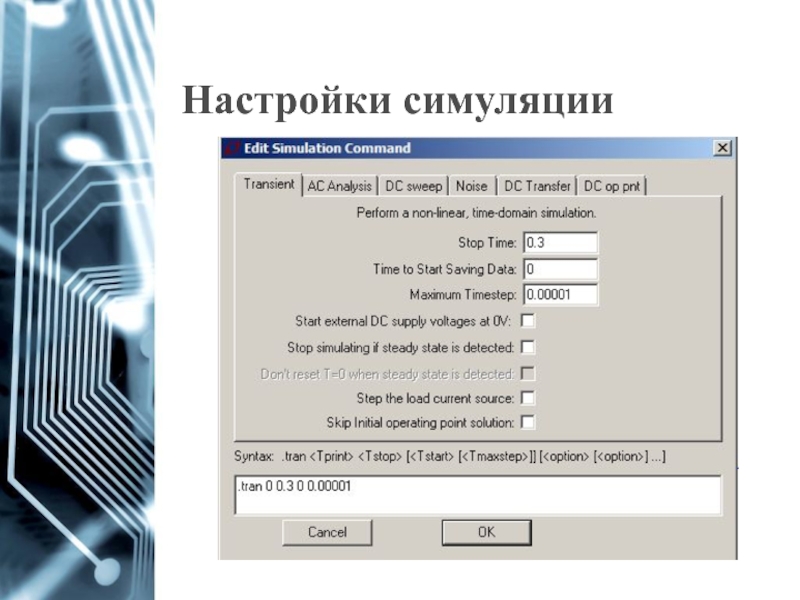
- 25. Настройки симуляции
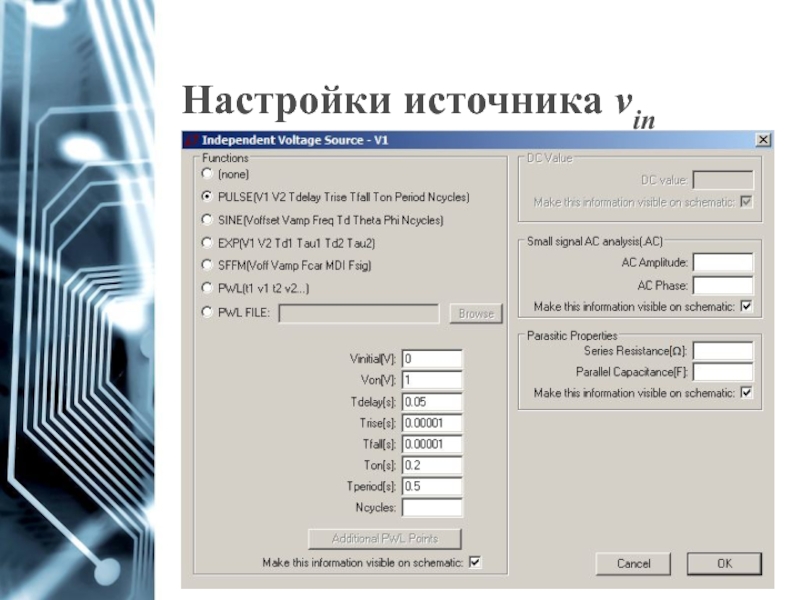
- 26. Настройки источника vin
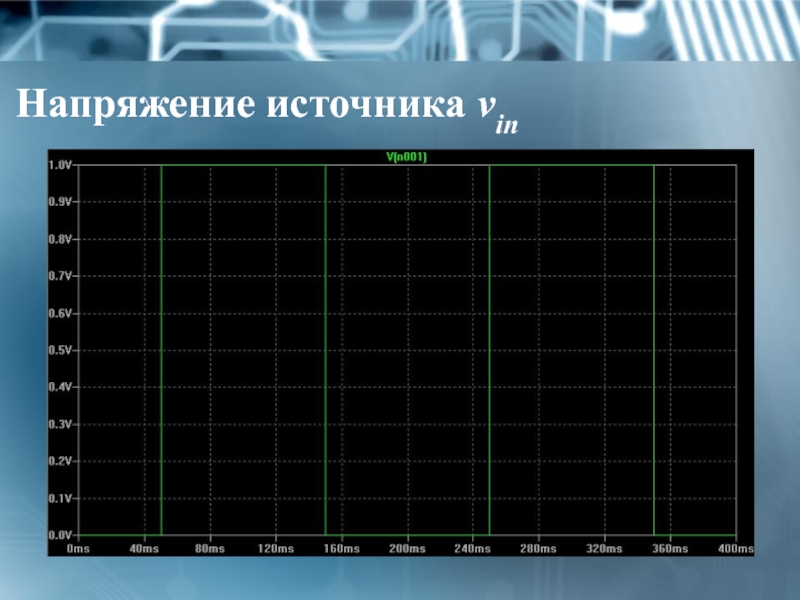
- 27. Напряжение источника vin
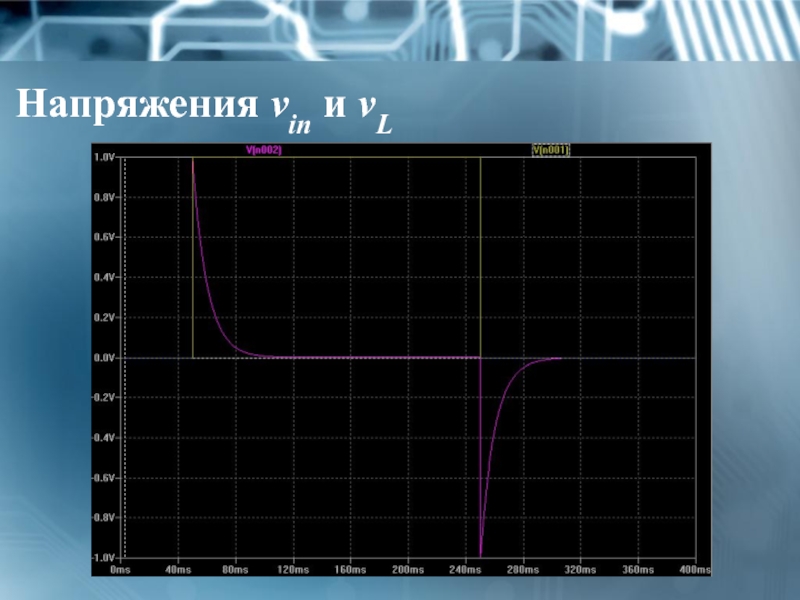
- 28. Напряжения vin и vL
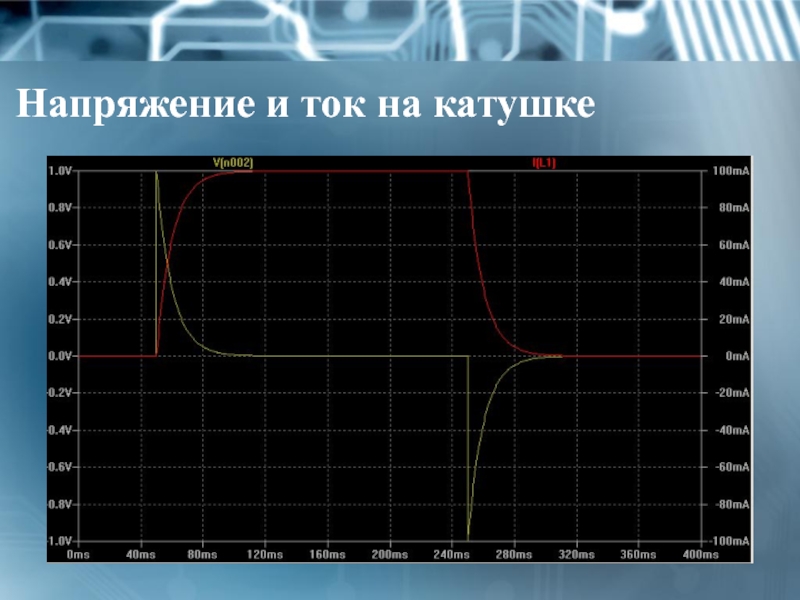
- 29. Напряжение и ток на катушке
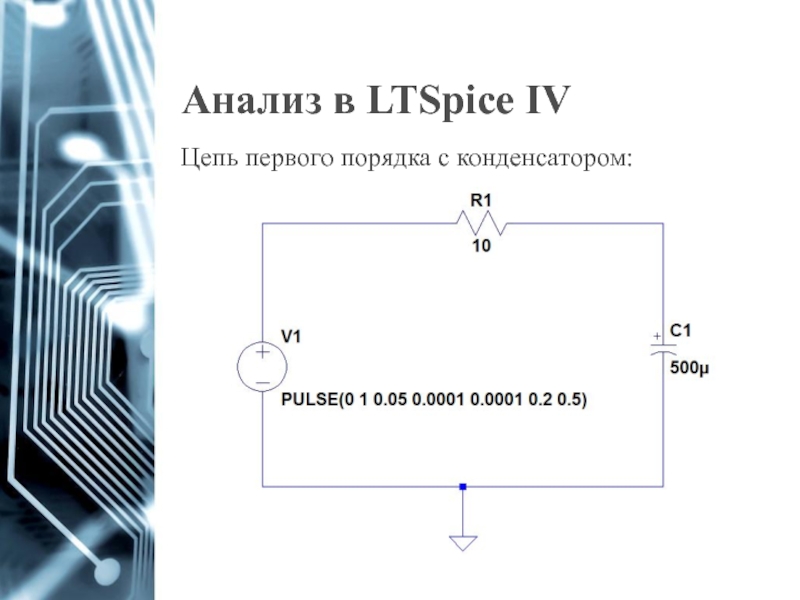
- 30. Анализ в LTSpice IV Цепь первого порядка с конденсатором:
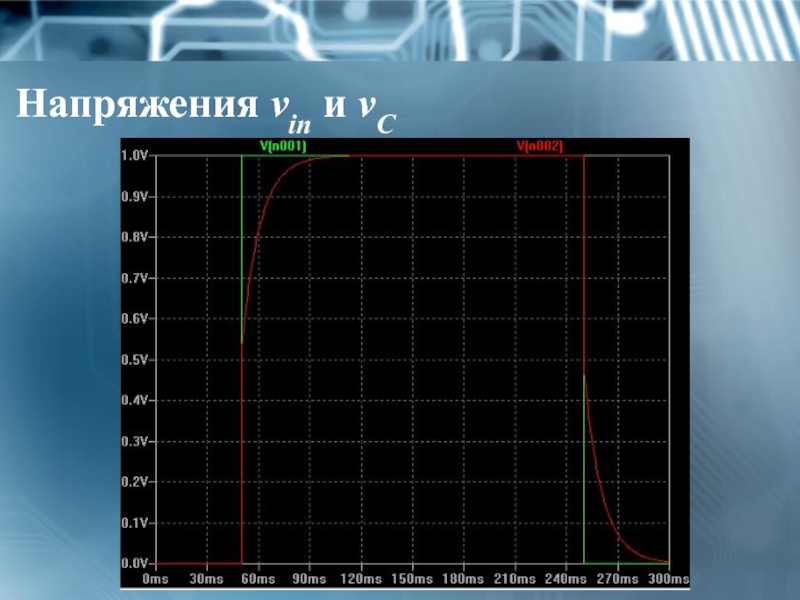
- 31. Напряжения vin и vС
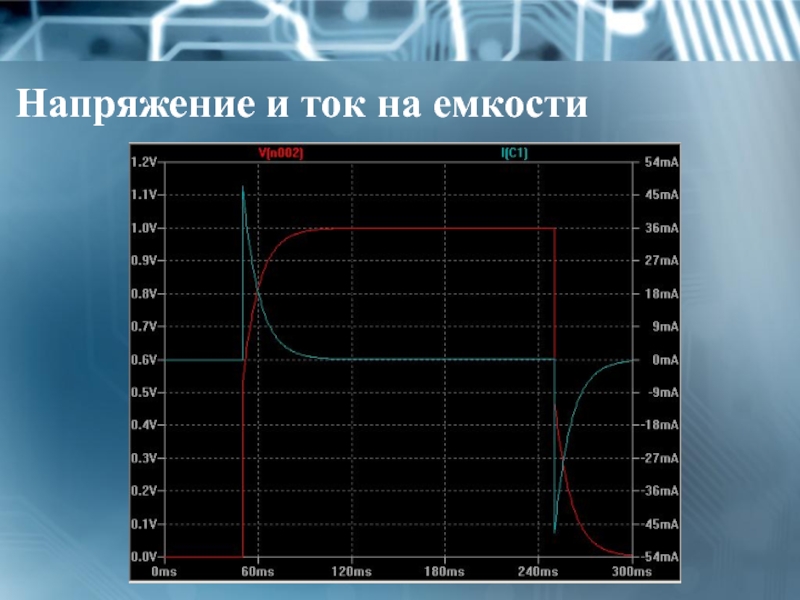
- 32. Напряжение и ток на емкости
- 33. Операторный метод Хевисайда Дифференциальное уравнение может быть
- 34. Преобразование Лапласа Для преобразования функции
- 35. Оригиналы и их изображения Оригинал Изображение А
- 36. Оригиналы и их изображения Оригинал Изображение
- 37. Формула разложения Переход от изображения
- 38. Формула разложения
- 39. Формула разложения Применим формулу разложения:
- 40. Операторный метод расчета Алгоритм расчета переходных процессов
- 41. Операторные изображения
- 42. Операторные изображения
- 43. Операторные изображения
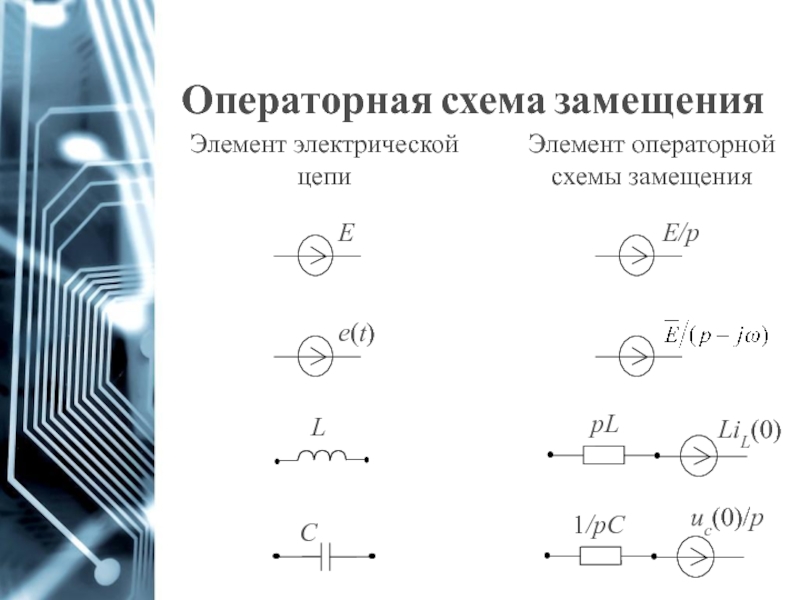
- 44. Операторная схема замещения
- 45. Расчет схемы первого порядка Определяем начальные
- 46. Расчет схемы первого порядка 2. Составляем
- 47. Расчет схемы первого порядка 3. Получение
- 48. Расчет схемы первого порядка 4. Применяем
- 49. Расчет схемы первого порядка Применяем теорему
- 50. Расчет схемы первого порядка Определяем
- 51. Расчет схемы первого порядка 2.
- 52. Расчет схемы первого порядка 3. Получение
- 53. Расчет схемы первого порядка 4. Применяем
- 54. Расчет схемы первого порядка Применяем теорему
- 55. Переходной процесс в цепи переменного тока Алгоритм
- 56. RL-цепь на переменном токе Определяем начальные
- 57. RL-цепь на переменном токе 2.
- 58. RL-цепь на переменном токе 4.
- 59. RL-цепь на переменном токе
- 60. RL-цепь на переменном токе 5. Записываем
- 61. RL-цепь на переменном токе Дифференцируем формулу для нахождения напряжения на катушке:
- 62. RL-цепь на переменном токе График изменения
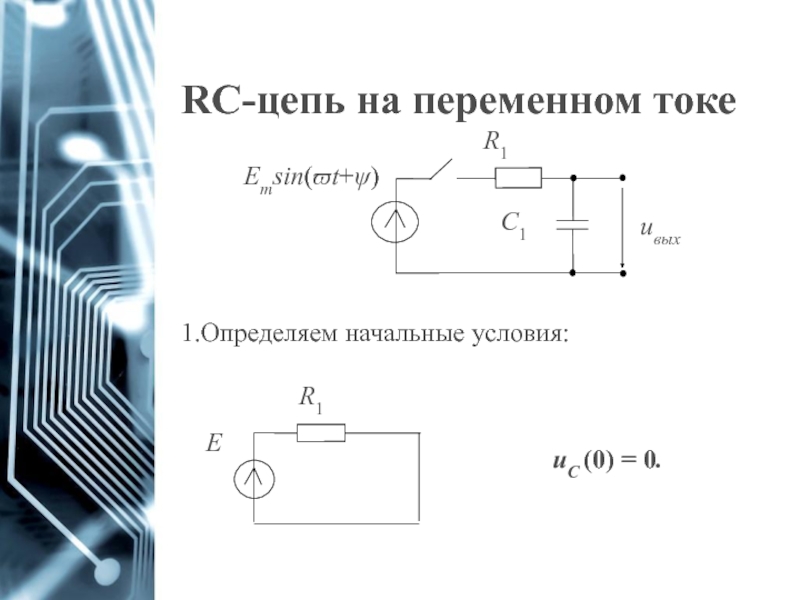
- 63. RC-цепь на переменном токе Определяем начальные условия: uС (0) = 0.
- 64. RC-цепь на переменном токе 2.
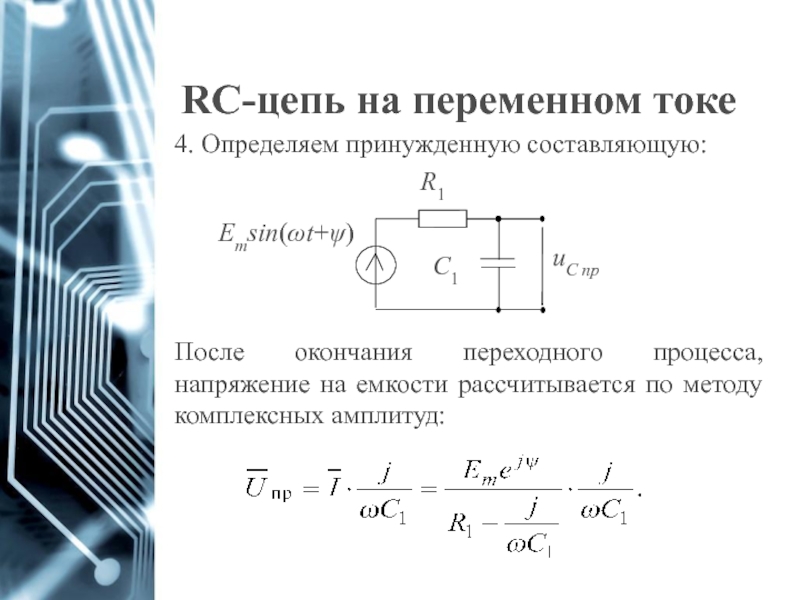
- 65. RC-цепь на переменном токе 4.
- 66. RC-цепь на переменном токе
- 67. RC-цепь на переменном токе 5. Записываем
- 68. RC-цепь на переменном токе Находим функцию
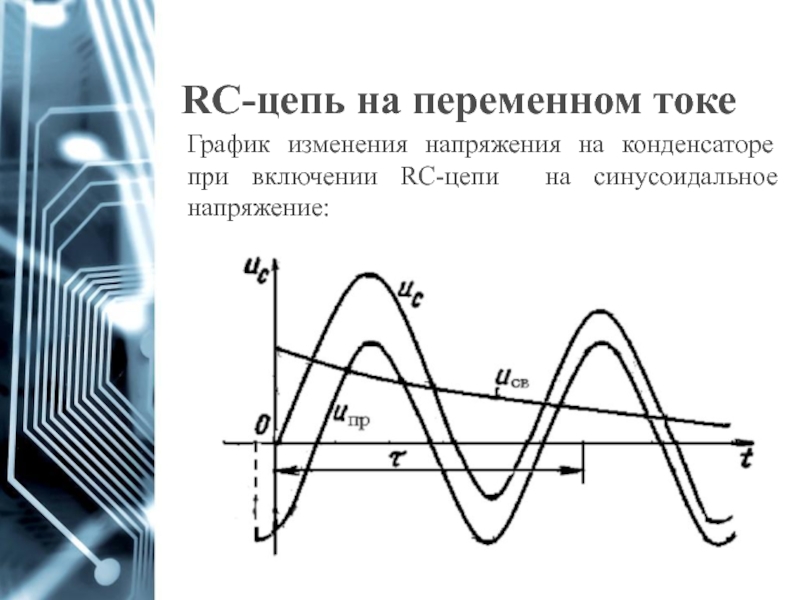
- 69. RC-цепь на переменном токе График изменения
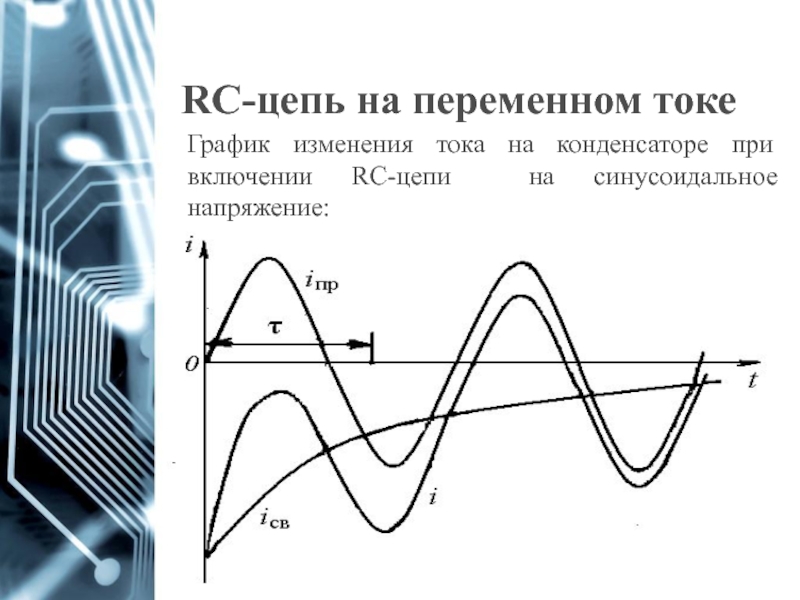
- 70. RC-цепь на переменном токе График изменения
- 71. Расчет схемы первого порядка Определяем начальные
- 72. Расчет схемы первого порядка 2. Составляем
- 73. Расчет схемы первого порядка 3. Получение
- 74. Расчет схемы первого порядка 4.
Слайд 2Переходные процессы
В линейной электрической цепи, содержащей реактивные элементы, при переходе от
Переходные процессы обусловлены законами коммутации, частными случаями закона сохранения энергии.
Условия возникновения переходных процессов:
а) наличие коммутации в цепи;
б) скачкообразно меняются параметры цепи;
в) скачкообразное изменение всей структуры цепи.
Слайд 3Законы коммутации
Первый закон:
в ветви электрической цепи с катушками индуктивности ток и
Второй закон:
напряжение на обкладках конденсатора и его заряд не могут измениться скачком, и сразу после коммутации они сохраняют те значения, которые имели до коммутации
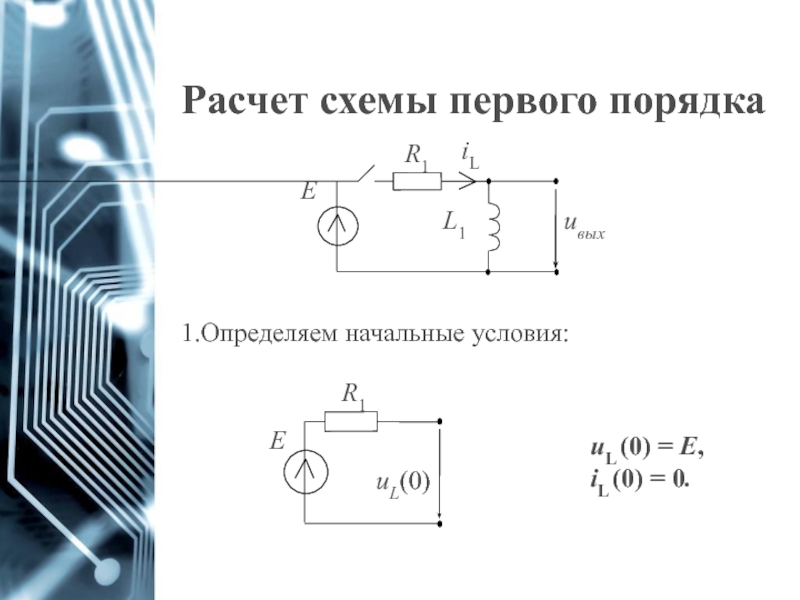
Слайд 4Начальные условия
Начальными условиями называются те значения токов и напряжений, которые были
Слайд 5Начальные условия
Начальными условиями называются те значения токов и напряжений, которые были
Слайд 6Математическое описание
Дифференциальное уравнение, описывающее переходный процесс в цепи с n независимыми
где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); f(t) – известное внешнее воздействие (напряжение и (или) ток источника электрической энергии); ak – k-й постоянный коэффициент, определяемый параметрами цепи.
Слайд 7Решение диф. уравнения
Решение дифференциального уравнения в общем случае имеет вид:
х
где хпр – принужденная составляющая, частное решение диф. уравнения (зависит от внешнего воздействия, определяется путем расчета стационарного режима работы схемы после окончания переходного процесса), хсв – свободная составляющая, общее решение диф. уравнения с нулевой правой частью (соответствует режиму, когда внешние (принуждающие) силы (источники энергии) не воздействуют на цепь).
Слайд 8Классический метод расчета
Алгоритм расчета переходных процессов классическим методом:
1) определение начальных условий;
2)
3) составление характеристического уравнения и расчет его корней (метод Эйлера);
4) расчет принужденной составляющей;
5) запись общего решения как суммы принужденной и свободной составляющих, определение постоянных интегрирования, построение графиков.
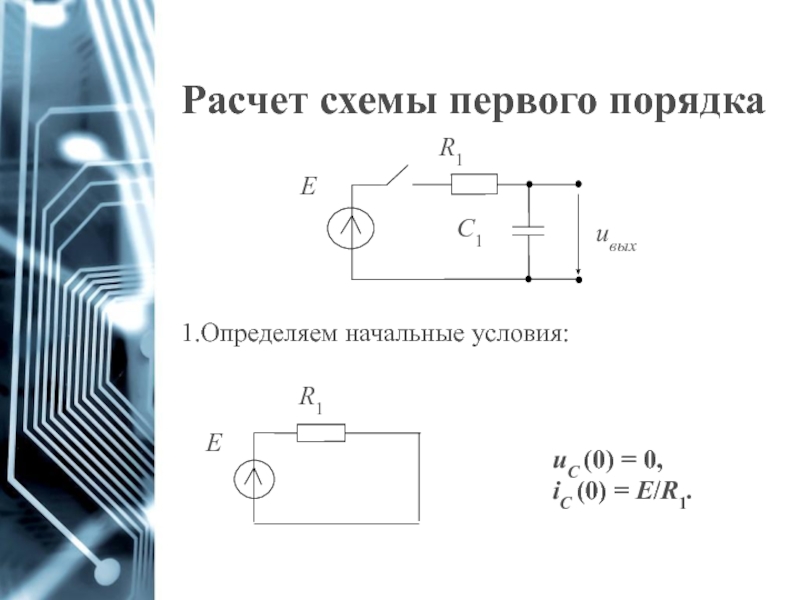
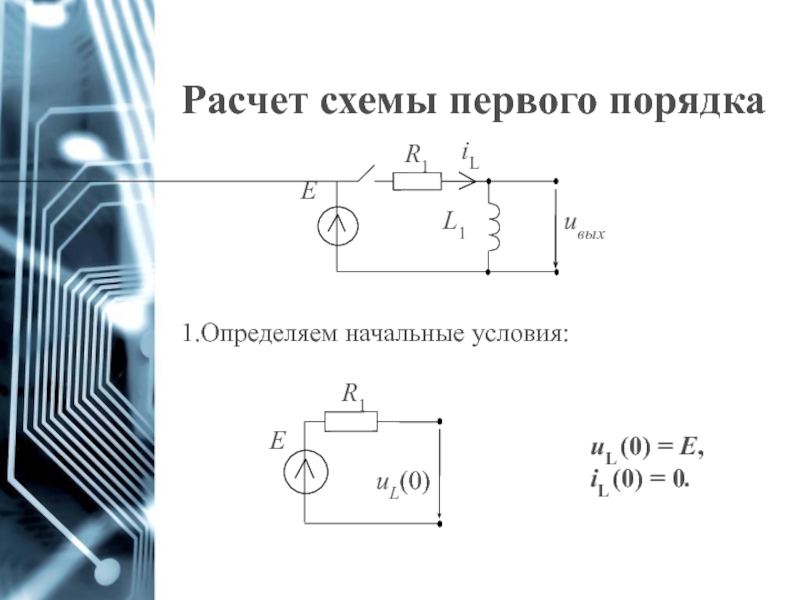
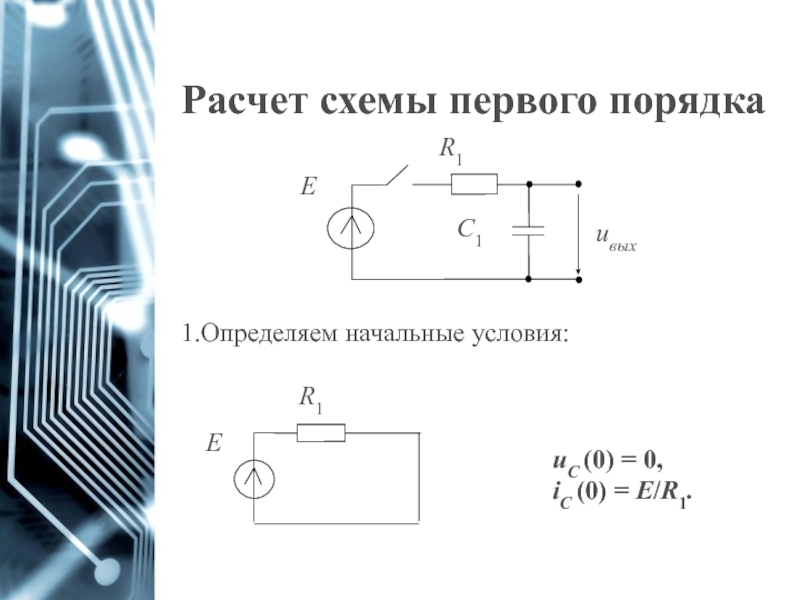
Слайд 10Расчет схемы первого порядка
Найдем производную для x(t):
Дифференциальную формулу напряжения на катушке
3. Решение для однородного дифференциального уравнения первого порядка записывается в виде:
Слайд 11Расчет схемы первого порядка
Составляем характеристическое уравнение при отсутствии входного воздействия:
Находим корень:
Для
Корень p определяет длительность переходного процесса через постоянную времени τ:
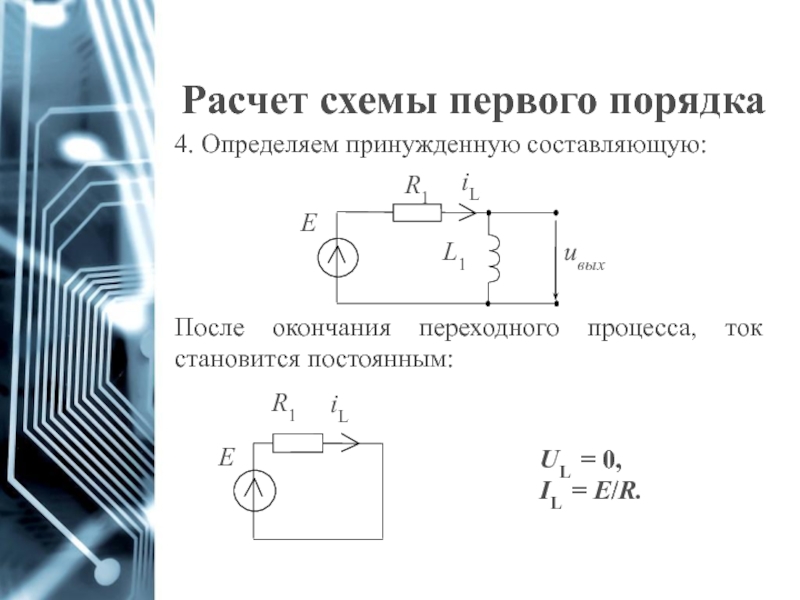
Слайд 12Расчет схемы первого порядка
4. Определяем принужденную составляющую:
После окончания переходного процесса, ток
Слайд 13Расчет схемы первого порядка
5. Записываем решение в общем виде:
Решаем уравнение при
=>
=>
Окончательное решение:
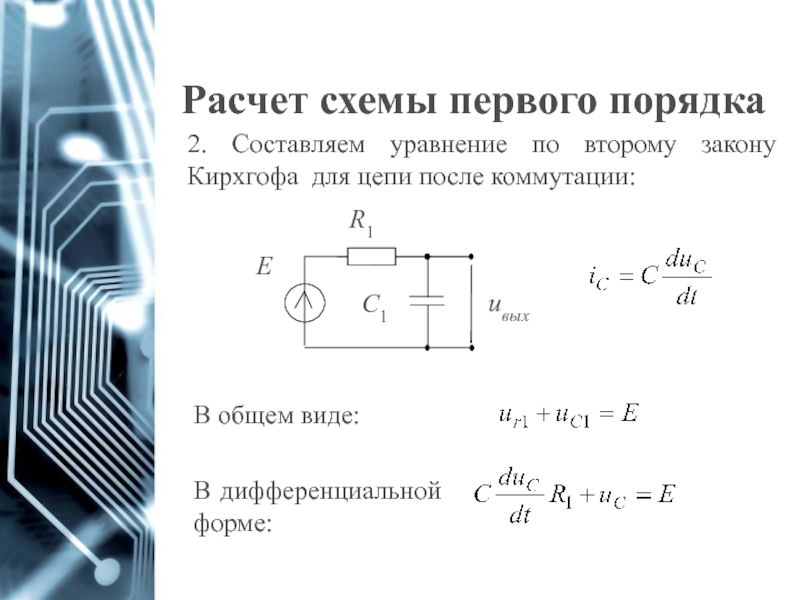
Слайд 17Расчет схемы первого порядка
2. Составляем уравнение по второму закону Кирхгофа для
В общем виде:
В дифференциальной форме:
Слайд 18Расчет схемы первого порядка
3. Решение для однородного дифференциального уравнения первого порядка
Найдем интеграл для x(t):
Дифференциальную формулу тока на емкости можно представить в операторной форме:
Слайд 19Расчет схемы первого порядка
Составляем характеристическое уравнение при отсутствии входного воздействия:
Находим корень:
Корень
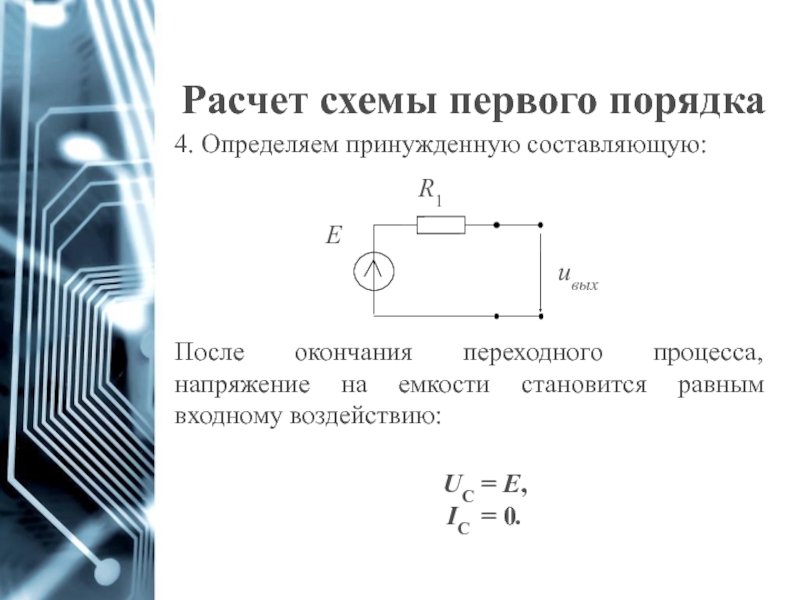
Слайд 20Расчет схемы первого порядка
4. Определяем принужденную составляющую:
После окончания переходного процесса, напряжение
UС = E,
IC = 0.
Слайд 21Расчет схемы первого порядка
5. Записываем решение в общем виде:
Решаем уравнение при
=>
=>
Окончательное решение:
Слайд 33Операторный метод Хевисайда
Дифференциальное уравнение может быть представлено операторным изображением.
Сложные математические операции
Полученные операторные уравнения решаются относительно комплексного переменного F(р) для искомой функции.
Заключительным этапом расчета переходных процессов операторным методом является нахождение оригинала функции по известному изображению.
Слайд 34Преобразование Лапласа
Для преобразования функции вещественного переменного f(t) в функцию комплексного переменного
Между изображением и оригиналом нет равенства, а есть только соответствие:
Известно более 1500 оригиналов и соответствующих им изображений.
Слайд 37Формула разложения
Переход от изображения к оригиналу возможен по теореме разложения с
Порядок расчета:
1) приравнивая F2(р) нулю, определяют корни р1, р2, р3 и т. д.;
2) вычисляют производную знаменателя дроби F (р) и подставляют в нее поочередно корни;
3) вычисляют числитель F1(р), подставляя в него корни;
4) рассчитывают оригинал f(t), производя вычисления отдельных слагаемых и суммируя их.
Слайд 38Формула разложения
Пример.
Обозначим F1(р)=120; F2(р)=р2+160 р+6000.
Найдем корни многочлена знаменателя F2(р)=0;
Слайд 39Формула разложения
Применим формулу разложения:
F1(p1)=F1(p2)=F1(p)=120
Производная знаменателя F2/ (р) = 2р +160.
Подставляем
F2/(p1)=2(-60)+160=40
F2/(p2)=2(-100)+160= -40
По формуле разложения найдем оригинал:
Слайд 40Операторный метод расчета
Алгоритм расчета переходных процессов операторным методом:
1) определение начальных условий;
2)
3) получение операторных функций токов и напряжений в дробно-рациональном виде;
4) представление знаменателя в виде уравнения в однородной форме, расчет его корней;
5) переход от операторного изображения к оригиналу с помощью таблиц или формулы разложения, построение графиков.
Слайд 42Операторные изображения
При нулевых начальных условиях:
По аналогии с комплексным сопротивлением вводится понятие
Операторные функции для тока на катушке и напряжения на емкости примут вид:
Слайд 43Операторные изображения
При ненулевых начальных условиях:
Эти слагаемые называют внутренними эдс. Они
учитывают энергию
На схеме замещения их моделируют введением дополнительных источников эдс. Направление источника совпадает с направлением тока через катушку и противоположно направлению напряжения на конденсаторе.
Слайд 46Расчет схемы первого порядка
2. Составляем операторную схему замещения и уравнение по
Слайд 47Расчет схемы первого порядка
3. Получение операторных функций тока и напряжений в
Слайд 48Расчет схемы первого порядка
4. Применяем теорему разложения для расчета оригинала тока.
Вычисляем производную знаменателя:
5. Находим оригинал тока по формуле разложения:
Слайд 49Расчет схемы первого порядка
Применяем теорему разложения для расчета оригинала функции напряжения.
Вычисляем производную знаменателя:
Находим оригинал напряжения по формуле разложения:
Слайд 51Расчет схемы первого порядка
2. Составляем операторную схему замещения и уравнение по
Слайд 52Расчет схемы первого порядка
3. Получение операторных функций тока и напряжений в
Слайд 53Расчет схемы первого порядка
4. Применяем теорему разложения. Находим корни:
Вычисляем производную знаменателя:
5.
Слайд 54Расчет схемы первого порядка
Применяем теорему разложения для расчета оригинала функции тока.
Вычисляем производную знаменателя:
Находим оригинал тока по формуле разложения:
Слайд 55Переходной процесс в цепи переменного тока
Алгоритм расчета переходных процессов в цепях
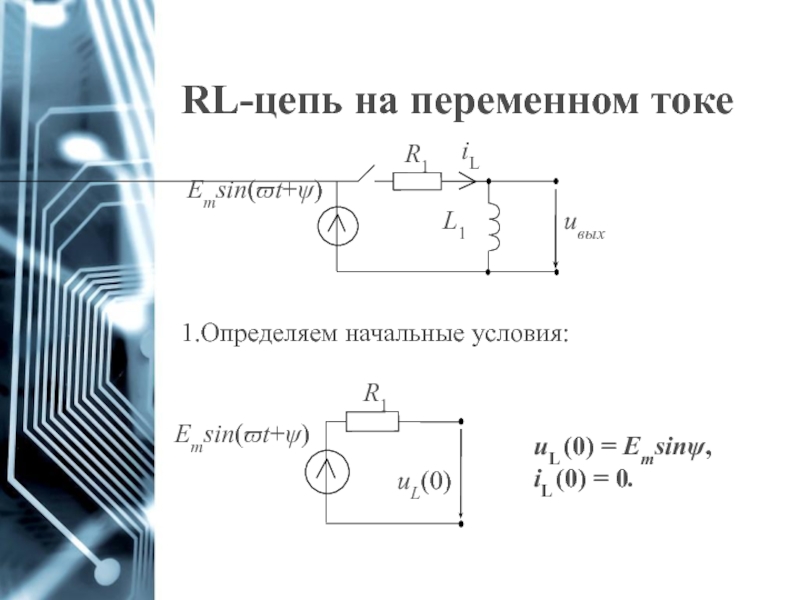
Слайд 56RL-цепь на переменном токе
Определяем начальные условия:
uL (0) = Еmsinψ,
iL (0)
Еmsin(ϖt+ψ)
Еmsin(ϖt+ψ)
Слайд 57RL-цепь на переменном токе
2. Составляем уравнение по второму закону Кирхгофа для
Еmsin(ϖt+ψ)
uL
3. Характеристическое уравнение и корень не зависят от характера внешнего воздействия:
L1
R1
iL
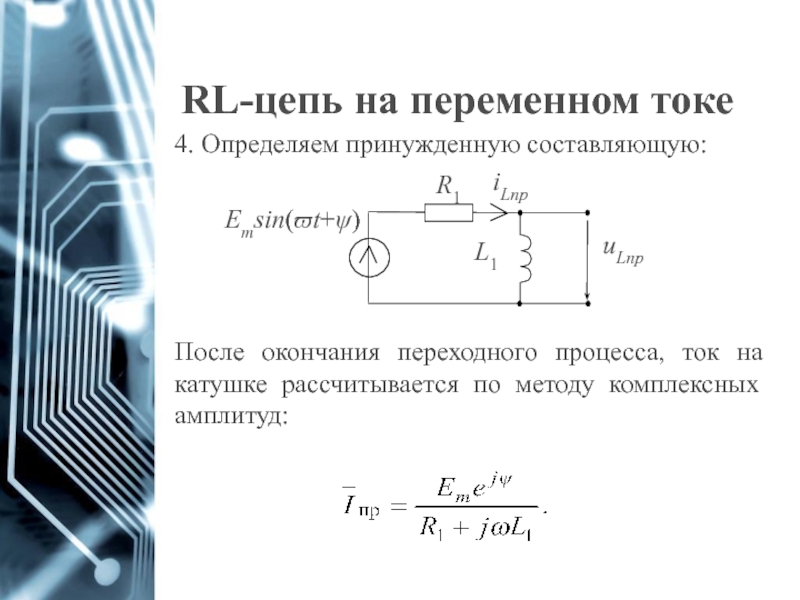
Слайд 58RL-цепь на переменном токе
4. Определяем принужденную составляющую:
После окончания переходного процесса, ток
Еmsin(ϖt+ψ)
uLпр
L1
R1
iLпр
Слайд 60RL-цепь на переменном токе
5. Записываем решение в общем виде:
Решаем уравнение при
Окончательное решение:
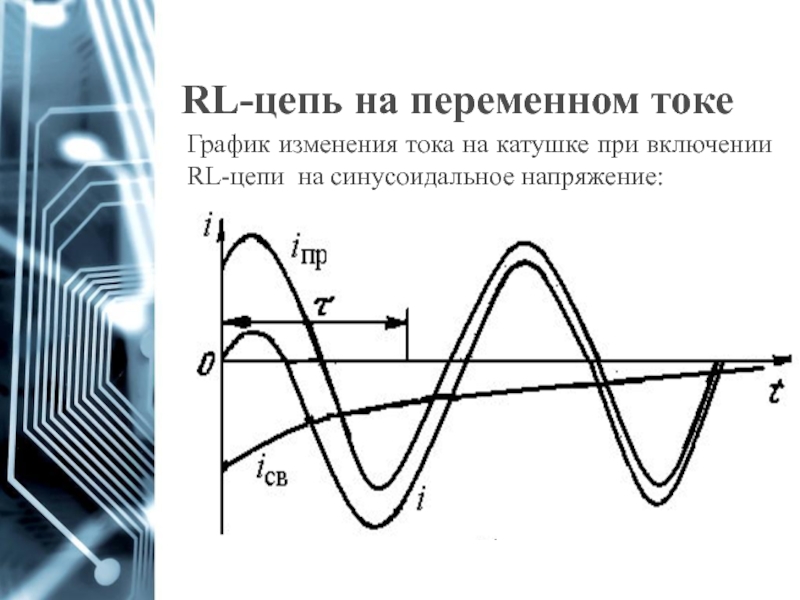
Слайд 62RL-цепь на переменном токе
График изменения тока на катушке при включении RL-цепи
Слайд 64RC-цепь на переменном токе
2. Составляем уравнение по второму закону Кирхгофа для
Еmsin(ωt+ψ)
uC = uC пр + uC св
3. Характеристическое уравнение и корень не зависят от характера внешнего воздействия:
Слайд 65RC-цепь на переменном токе
4. Определяем принужденную составляющую:
После окончания переходного процесса, напряжение
Еmsin(ωt+ψ)
uC пр
Слайд 67RC-цепь на переменном токе
5. Записываем решение в общем виде:
Решаем уравнение при
Окончательное решение:
Слайд 68RC-цепь на переменном токе
Находим функцию тока на емкости. Вынужденное значение силы
Свободная составляющая:
Слайд 69RC-цепь на переменном токе
График изменения напряжения на конденсаторе при включении RC-цепи
Слайд 70RC-цепь на переменном токе
График изменения тока на конденсаторе при включении RC-цепи
Слайд 72Расчет схемы первого порядка
2. Составляем операторную схему замещения и уравнение по
Слайд 73Расчет схемы первого порядка
3. Получение операторных функций тока и напряжений в
Слайд 74Расчет схемы первого порядка
4. Применяем теорему разложения для расчета оригинала тока.
Вычисляем производную знаменателя:
5. Находим оригинал тока по формуле разложения: