- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физические основы защиты информации от утечки по каналам побочных электромагнитных излучений и наводок презентация
Содержание
- 1. Физические основы защиты информации от утечки по каналам побочных электромагнитных излучений и наводок
- 2. Литература 1. Пименов
- 3. Основные характеристики поля и среды ФО ПЭМИН
- 4. Основные характеристики поля и среды ФО ПЭМИН
- 5. ФО ПЭМИН Основные характеристики поля и среды
- 6. ФО ПЭМИН Классификация сред
- 7. ФО ПЭМИН Классификация сред
- 8. ФО ПЭМИН Классификация сред
- 9. Полная система уравнений электродинамики Уравнения Максвелла (Джеймс
- 10. ФО ПЭМИН Полная система уравнений электродинамики
- 11. ФО ПЭМИН Полная система уравнений электродинамики
- 12. ФО ПЭМИН Полная система уравнений электродинамики Теорема
- 13. ФО ПЭМИН Полная система уравнений электродинамики Закон
- 14. Закон сохранения заряда ФО ПЭМИН Полная система
- 15. Закон Ома в дифференциальной форме ФО ПЭМИН
- 16. Интегральная форма уравнений Максвелла: ФО ПЭМИН Полная
- 17. ФО ПЭМИН Полная система уравнений электродинамики Дифференциальная
- 18. Классификация электромагнитных явлений 1. Статическое поле:
- 19. ФО ПЭМИН Классификация электромагнитных явлений 2. Стационарное
- 20. Граничные условия ФО ПЭМИН - нормальная составляющая - тангенциальная составляющая
- 21. Нормальные составляющие магнитного поля ФО ПЭМИН
- 22. Нормальные составляющие электрического поля ФО
- 23. ФО ПЭМИН Граничные условия Тангенциальные составляющие электрического
- 24. ФО ПЭМИН Граничные условия Тангенциальные составляющие магнитного
- 25. ФО ПЭМИН Граничные условия
- 26. ФО ПЭМИН Монохроматическое поле Метод комплексных амплитуд
- 27. ФО ПЭМИН Монохроматическое поле Система уравнений монохроматического
- 28. ФО ПЭМИН Монохроматическое поле аналогично:
- 29. Баланс энергии ЭМП ФО ПЭМИН
- 30. ФО ПЭМИН Энергетические соотношения в ЭМП
- 31. ФО ПЭМИН Энергетические соотношения в ЭМП Теорема
- 32. ФО ПЭМИН Энергетические соотношения в ЭМП
- 33. ФО ПЭМИН Энергетические соотношения в ЭМП
- 34. Волновые уравнения Прямая задача: ФО ПЭМИН Заданы
- 35. ФО ПЭМИН Волновые уравнения Аналогично:
- 36. ФО ПЭМИН Волновые уравнения Если
- 37. ФО ПЭМИН Для монохроматического поля: Волновые уравнения
- 38. Электродинамические потенциалы ФО ПЭМИН Потенциалы…
- 39. ФО ПЭМИН Электродинамические потенциалы Калибровка: Запаздывающие потенциалы
- 40. ФО ПЭМИН Электродинамические потенциалы Для монохроматического поля
- 41. Теорема единственности ФО ПЭМИН
- 42. Излучение ЭМ волн Элементарный электрический вибратор ФО
- 43. ФО ПЭМИН Излучение ЭМ волн Определяем векторы поля
- 44. ФО ПЭМИН Излучение ЭМ волн
- 45. Излучение ЭМ волн ФО ПЭМИН
- 46. ФО ПЭМИН Излучение ЭМ волн Дальняя зона
- 47. ФО ПЭМИН Излучение ЭМ волн Ближняя зона
- 48. ФО ПЭМИН Излучение ЭМ волн - как эл. поле заряда - как магн. поле тока
- 49. ФО ПЭМИН Излучение ЭМ волн Диаграммы направленности
- 50. ФО ПЭМИН Излучение ЭМ волн Мощность излучения
- 51. ФО ПЭМИН Излучение ЭМ волн В вакууме:
- 52. ФО ПЭМИН Излучение ЭМ волн Принцип перестановочной
- 53. ФО ПЭМИН Излучение ЭМ волн
- 54. ФО ПЭМИН Излучение ЭМ волн
- 55. ФО ПЭМИН Излучение ЭМ волн Элементарная рамка
- 56. ФО ПЭМИН Излучение ЭМ волн Эквивалентные источники
- 57. ФО ПЭМИН Излучение ЭМ волн Принцип Гюйгенса Элемент Гюйгенса
- 58. ФО ПЭМИН Излучение ЭМ волн
- 59. ФО ПЭМИН Плоские ЭМВ Среда без потерь:
- 60. ФО ПЭМИН Плоские ЭМВ
- 61. ФО ПЭМИН Плоские ЭМВ Среда c потерями:
- 62. ФО ПЭМИН Плоские ЭМВ
- 63. ФО ПЭМИН Плоские ЭМВ Диэлектрик:
- 64. ФО ПЭМИН Плоские ЭМВ Проводник:
- 65. ФО ПЭМИН Плоские ЭМВ
- 66. ФО ПЭМИН Плоские ЭМВ Поляризация волн
- 67. ФО ПЭМИН Плоские ЭМВ
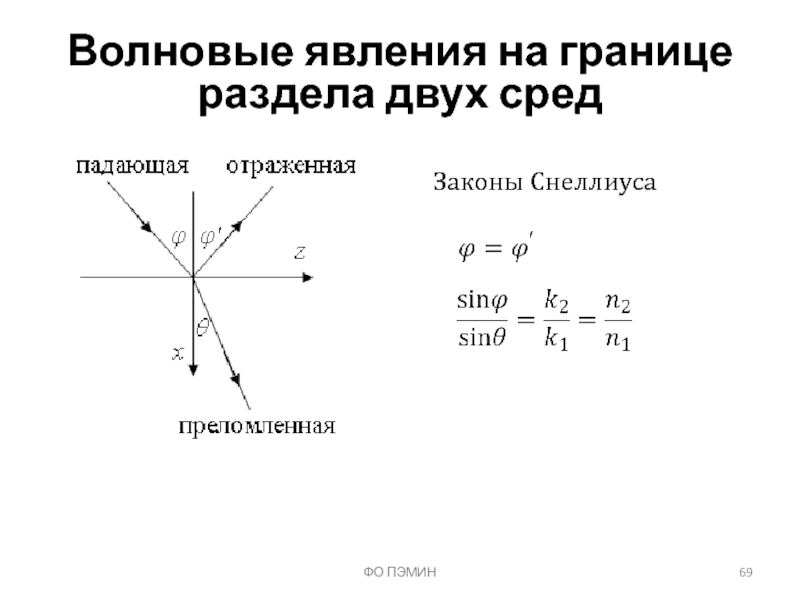
- 68. ФО ПЭМИН Волновые явления на границе раздела
- 69. ФО ПЭМИН Волновые явления на границе раздела двух сред Законы Снеллиуса
- 70. ФО ПЭМИН Волновые явления на границе раздела
- 71. ФО ПЭМИН Волновые явления на границе раздела
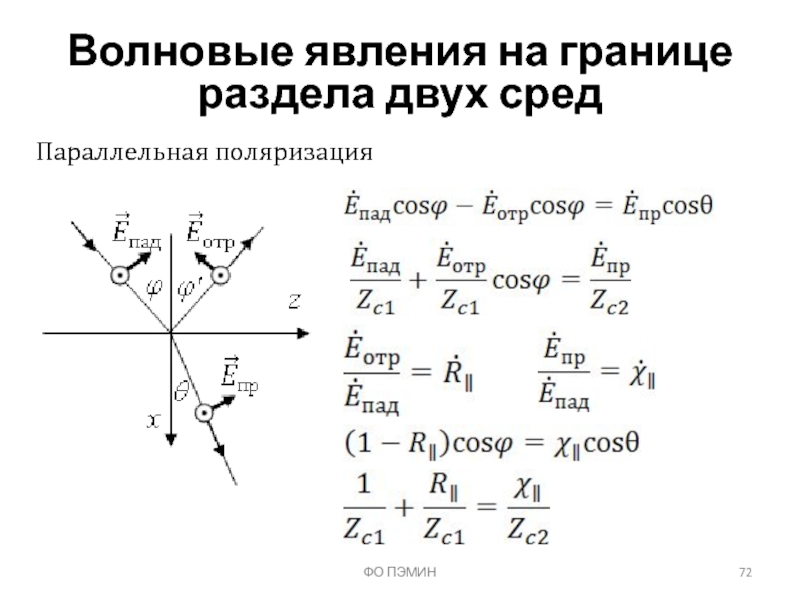
- 72. ФО ПЭМИН Волновые явления на границе раздела
- 73. ФО ПЭМИН Волновые явления на границе раздела
- 74. ФО ПЭМИН Волновые явления на границе раздела двух сред Нормальное падение
- 75. ФО ПЭМИН Волновые явления на границе раздела
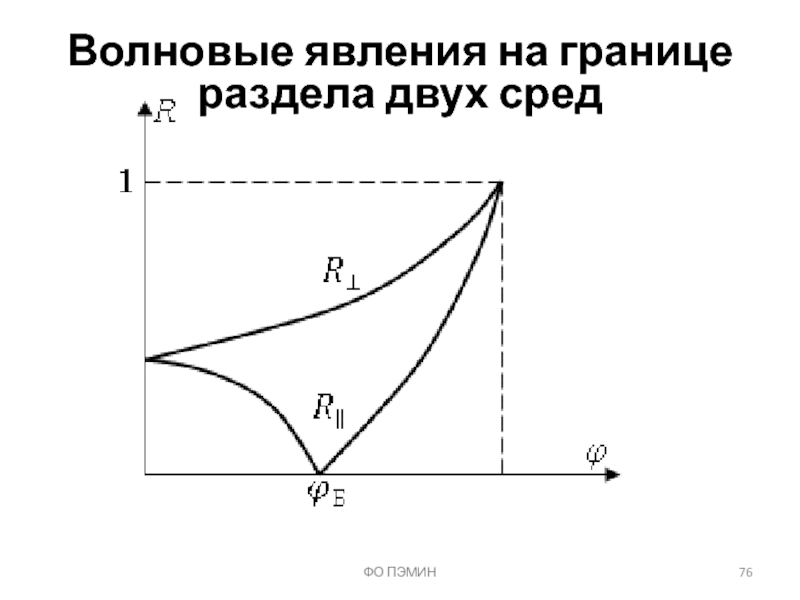
- 76. ФО ПЭМИН Волновые явления на границе раздела двух сред
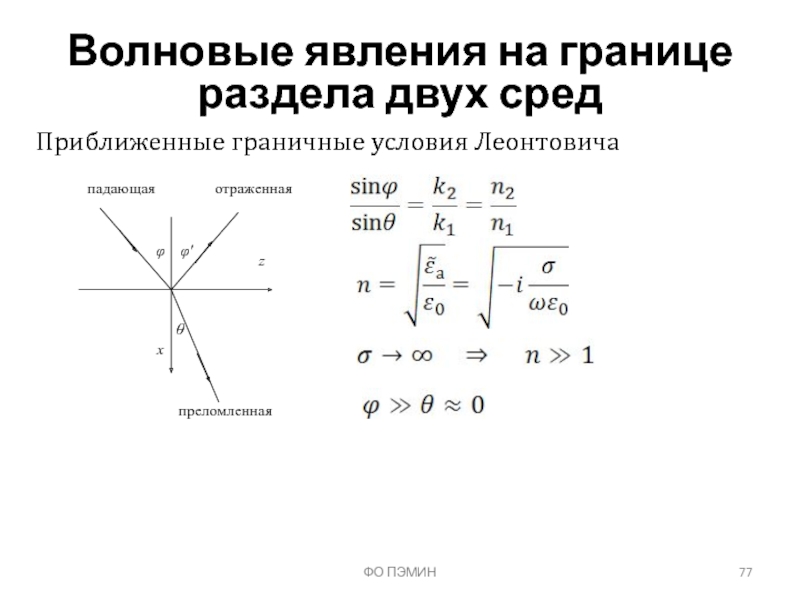
- 77. ФО ПЭМИН Волновые явления на границе раздела
- 78. ФО ПЭМИН Волновые явления на границе раздела двух сред
- 79. Поверхностный эффект ФО ПЭМИН Напряженность поля у плоской границы проводника
- 80. ФО ПЭМИН Поверхностный эффект
- 81. ФО ПЭМИН Поверхностный эффект Толщина скин-слоя Δ - толщина скин-слоя
- 82. ФО ПЭМИН Поверхностный эффект Поверхностный импеданс
- 83. ФО ПЭМИН Поверхностный эффект Потери энергии в
- 84. ФО ПЭМИН Поверхностный эффект Электромагнитный экран Тонкий экран (медь, f=1 ГГц: d
- 85. Постановка задачи дифракции в виде интегрального уравнения
- 86. ФО ПЭМИН Постановка задачи дифракции в виде
- 87. ФО ПЭМИН Постановка задачи дифракции в виде интегрального уравнения
- 88. ФО ПЭМИН Постановка задачи дифракции в виде
- 89. Тонкопроволочное приближение ФО ПЭМИН 1) на
- 90. ФО ПЭМИН Тонкопроволочное приближение – интегральное
- 91. ФО ПЭМИН Тонкопроволочное приближение (ядра Фредгольмовского
- 92. Уравнения Фредгольма 2-го рода ФО ПЭМИН Осесимметричное возбуждение
- 93. ФО ПЭМИН Уравнения Фредгольма 2-го рода
- 94. ФО ПЭМИН Уравнения Фредгольма 2-го рода
- 95. Области применения уравнений Фредгольма ФО ПЭМИН 2-го: a=0,005λ 1-го: a=0,0125λ a=0,05λ N=24
- 96. Мера обусловленности μ: ФО ПЭМИН Области применения
- 97. Методы решения ИУ Проекционная схема Бубнова-Галеркина ФО
- 98. ФО ПЭМИН Методы решения ИУ Из требования
- 99. Метод моментов. Проекционные методы ФО ПЭМИН Методы
- 100. ФО ПЭМИН Методы решения ИУ Проблема выбора
- 101. ФО ПЭМИН Методы решения ИУ Базисы полной
- 102. ФО ПЭМИН Методы решения ИУ Косинусоидальный базис
- 103. ФО ПЭМИН Базисы частичных подобластей Методы решения
- 104. ФО ПЭМИН Методы решения ИУ Кусочно-линейный и кусочно-синусоидальный базисы
- 105. ФО ПЭМИН Методы решения ИУ Квазипериодические кусочно-синусоидальные
- 106. ФО ПЭМИН Методы решения ИУ Если
- 107. ФО ПЭМИН Методы решения ИУ Центры отрезков
- 108. ФО ПЭМИН Методы решения ИУ Использование ККФ-базиса
- 109. ФО ПЭМИН Методы решения ИУ Формализация сторонних
- 110. ФО ПЭМИН Методы решения ИУ Задание стороннего
- 111. ФО ПЭМИН Методы решения ИУ Метод коллокации
- 112. ФО ПЭМИН Методы решения ИУ Метод Галеркина
Слайд 1ФИЗИЧЕСКИЕ ОСНОВЫ ЗАЩИТЫ ИНФОРМАЦИИ ОТ УТЕЧКИ ПО КАНАЛАМ ПОБОЧНЫХ ЭЛЕКТРОМАГНИТНЫХ ИЗЛУЧЕНИЙ
Слайд 2Литература
1. Пименов Ю.В., Вольман В.И., Муравцов А.Д.
2. Бузова М.А., Юдин В.В. Проектирование проволочных антенн на основе интегральных уравнений: Учебное пособие для ВУЗов. – М.: Радио и связь, 2005.
3. Кочержевский Г. Н. Антенно-фидерные устройства. М.: Связь. 1972.
4. Бузов Г.А., Калинин С.В., Кондратьев А.В. Защита от утечки информации по техническим каналам. Учебное пособие. – М.: Горячая линия - Телеком, 2005.
5. Хореев А.А. Защита информации от утечки по техническим каналам. Часть 1. Технические каналы утечки информации. – М.: ГТК РФ, 1998.
ФО ПЭМИН
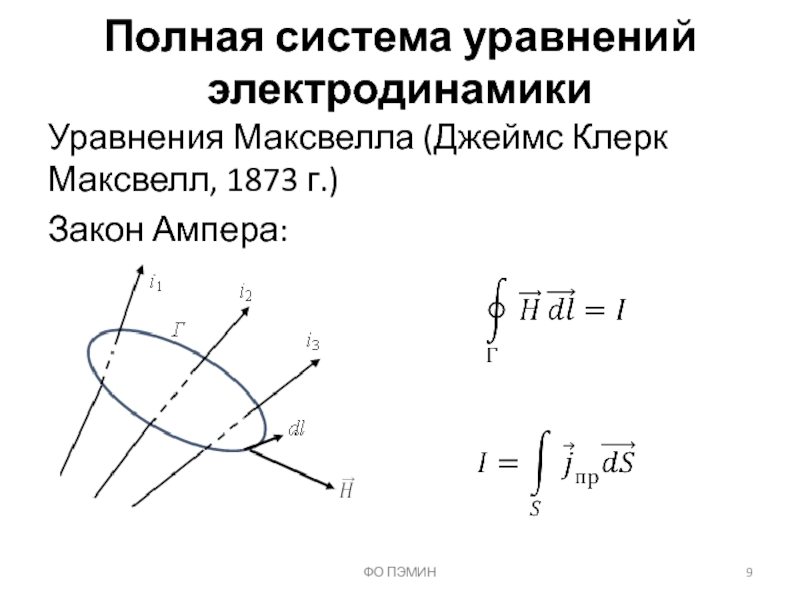
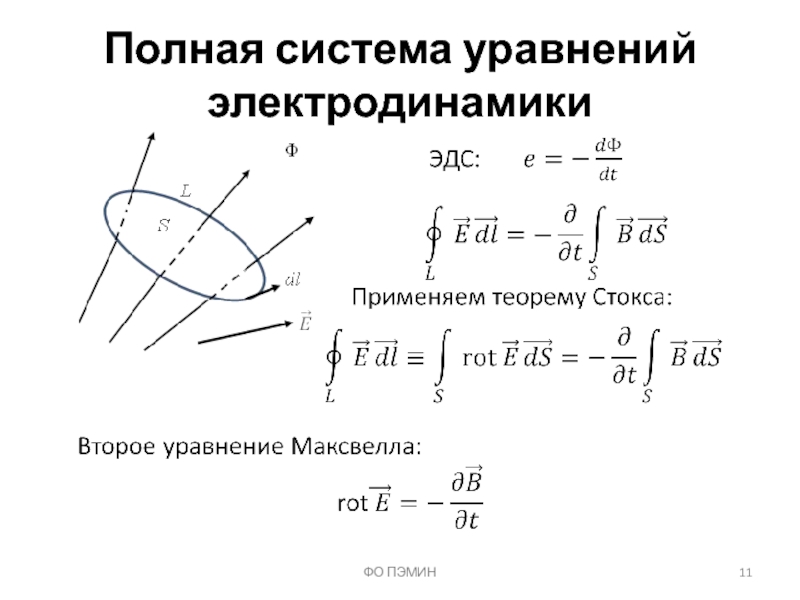
Слайд 9Полная система уравнений электродинамики
Уравнения Максвелла (Джеймс Клерк Максвелл, 1873 г.)
Закон Ампера:
ФО ПЭМИН
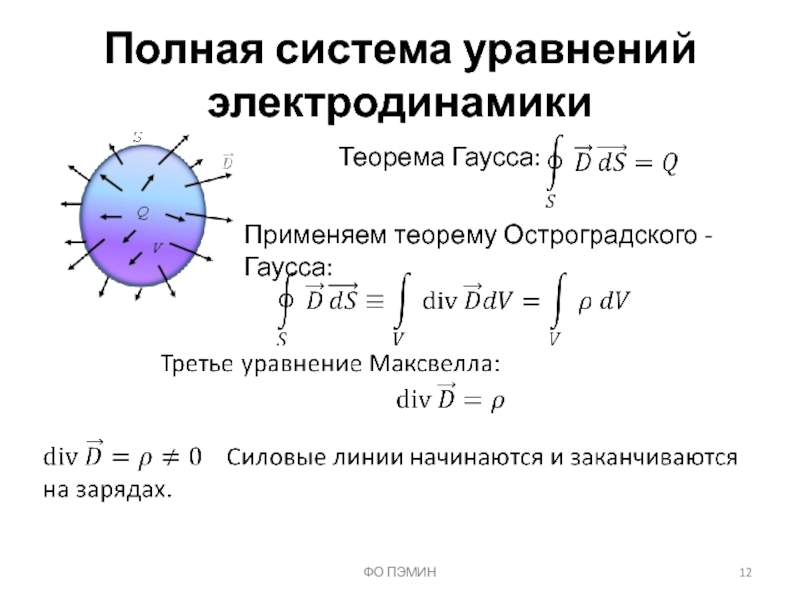
Слайд 12ФО ПЭМИН
Полная система уравнений электродинамики
Теорема Гаусса:
Применяем теорему Остроградского - Гаусса:
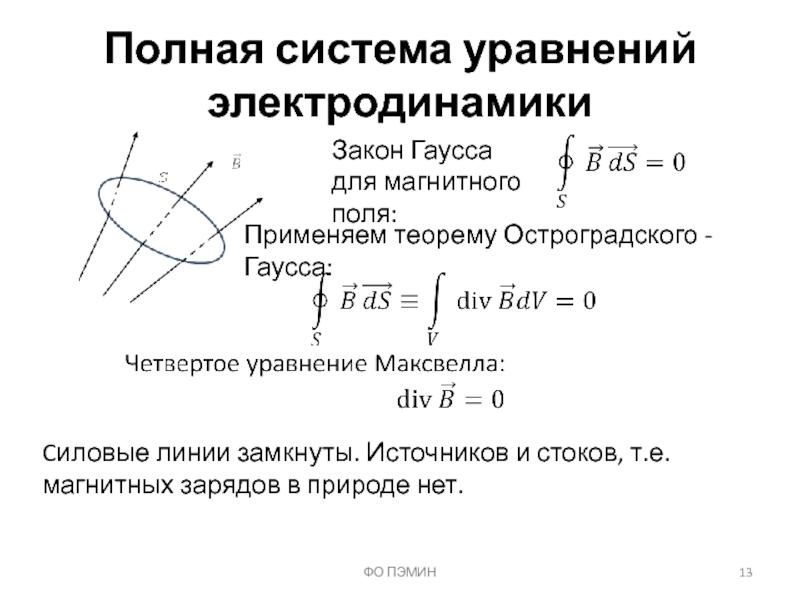
Слайд 13ФО ПЭМИН
Полная система уравнений электродинамики
Закон Гаусса для магнитного поля:
Применяем теорему Остроградского
Cиловые линии замкнуты. Источников и стоков, т.е. магнитных зарядов в природе нет.
Слайд 14Закон сохранения заряда
ФО ПЭМИН
Полная система уравнений электродинамики
Закон непрерывности линий полного тока
Слайд 16Интегральная форма уравнений Максвелла:
ФО ПЭМИН
Полная система уравнений электродинамики
1-е
2-е
3-е
4-е
Слайд 17ФО ПЭМИН
Полная система уравнений электродинамики
Дифференциальная форма уравнений Максвелла:
1-е
2-е
3-е
4-е
Уравнение непрерывности:
Закон сохранения заряда:
Закон
При наличии сторонних токов и зарядов:
Материальные уравнения:
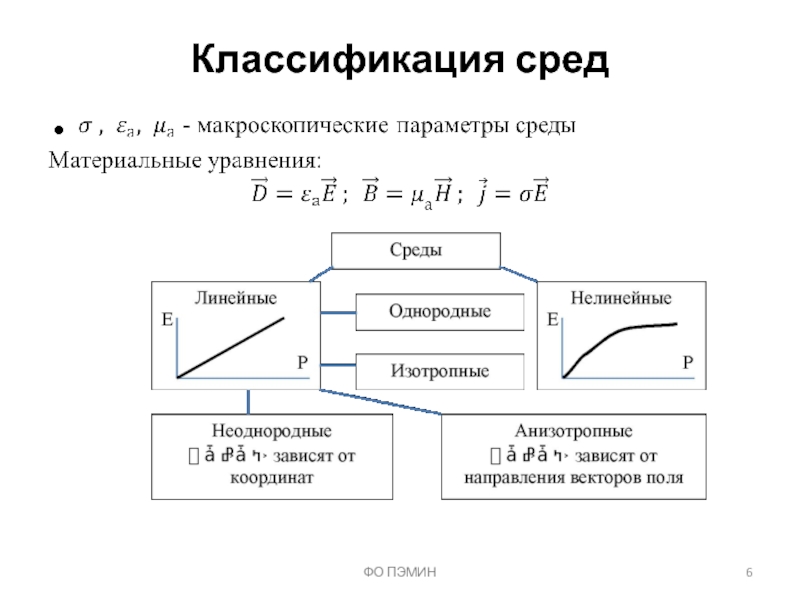
Слайд 18Классификация электромагнитных явлений
1. Статическое поле:
ФО ПЭМИН
Электрическое и магнитное поля независимы
Система уравнений электростатики:
Система уравнений магнитостатики:
Слайд 19ФО ПЭМИН
Классификация электромагнитных явлений
2. Стационарное поле:
3. Квазистационарное поле:
4. Быстропеременное поле:
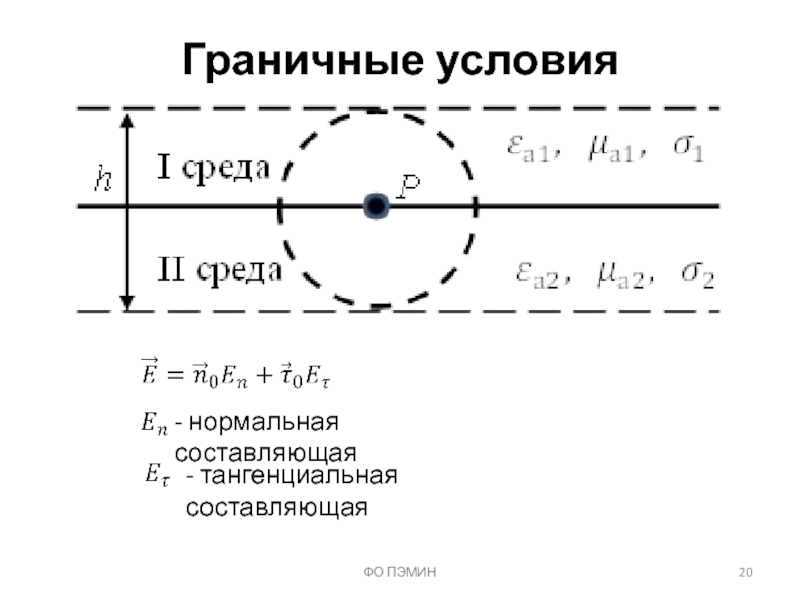
Слайд 24ФО ПЭМИН
Граничные условия
Тангенциальные составляющие магнитного поля
При наличии поверхностных токов:
Слайд 25ФО ПЭМИН
Граничные условия
Полная система граничных условий:
Для идеально проводящей поверхности:
Слайд 26ФО ПЭМИН
Монохроматическое поле
Метод комплексных амплитуд
- комплексная амплитуда
Аналогично для векторов:
компл. ампл.
Слайд 27ФО ПЭМИН
Монохроматическое поле
Система уравнений монохроматического поля
- комплексная диэлектрическая проницаемость
Аналогично:
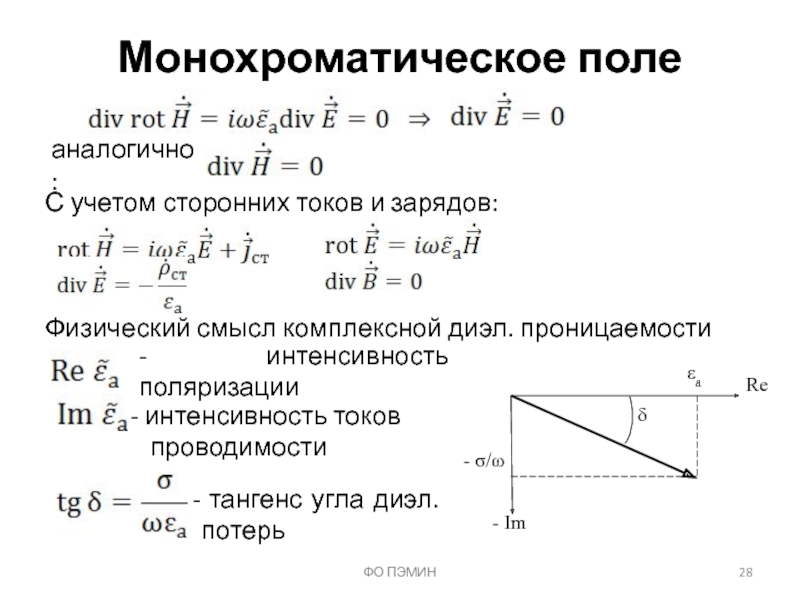
Слайд 28ФО ПЭМИН
Монохроматическое поле
аналогично:
С учетом сторонних токов и зарядов:
Физический смысл комплексной диэл.
- интенсивность поляризации
интенсивность токов
проводимости
тангенс угла диэл. потерь
Слайд 30ФО ПЭМИН
Энергетические соотношения в ЭМП
- вектор Пойнтинга (вектор ППЭ)
Теорема Умова-Пойнтинга
Слайд 31ФО ПЭМИН
Энергетические соотношения в ЭМП
Теорема Умова-Пойнтинга в комплексной форме
Среднее за период:
Слайд 34Волновые уравнения
Прямая задача:
ФО ПЭМИН
Заданы
Определяют
Обратная задача:
Заданы
Определяют
Для мгновенных значений векторов поля:
- оператор Лапласа
Слайд 40ФО ПЭМИН
Электродинамические потенциалы
Для монохроматического поля
Объемный сторонний ток
Поверхностный сторонний ток
Линейный сторонний ток
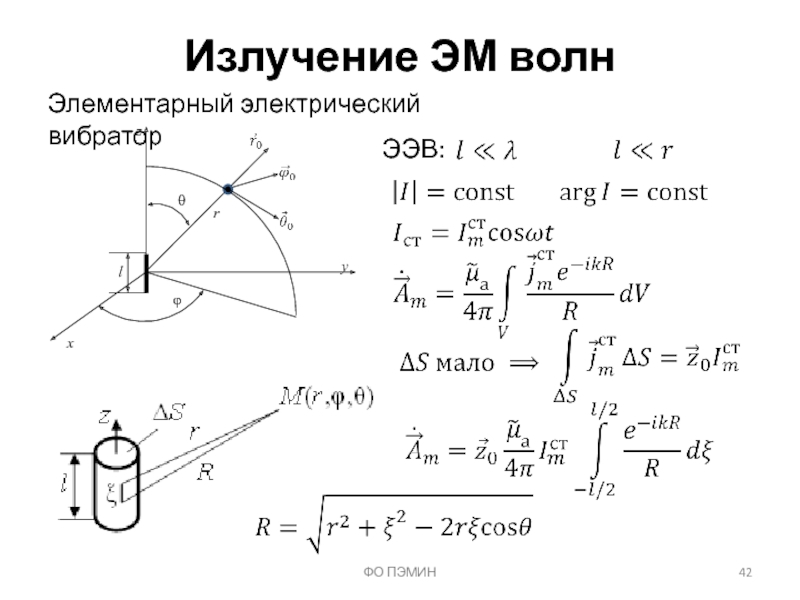
Слайд 46ФО ПЭМИН
Излучение ЭМ волн
Дальняя зона
Взаимно ортогональны. Синфазны.
Фазовая скорость:
(сфер.волна, распр. со скор.
Перенос энергии:
Слайд 56ФО ПЭМИН
Излучение ЭМ волн
Эквивалентные источники ЭМП
Произвольная замкнутая поверхность S.
Внутри локализованы
Заменяем действие реальных источников на действие эквивалентных (фиктивных):
На поверхности:
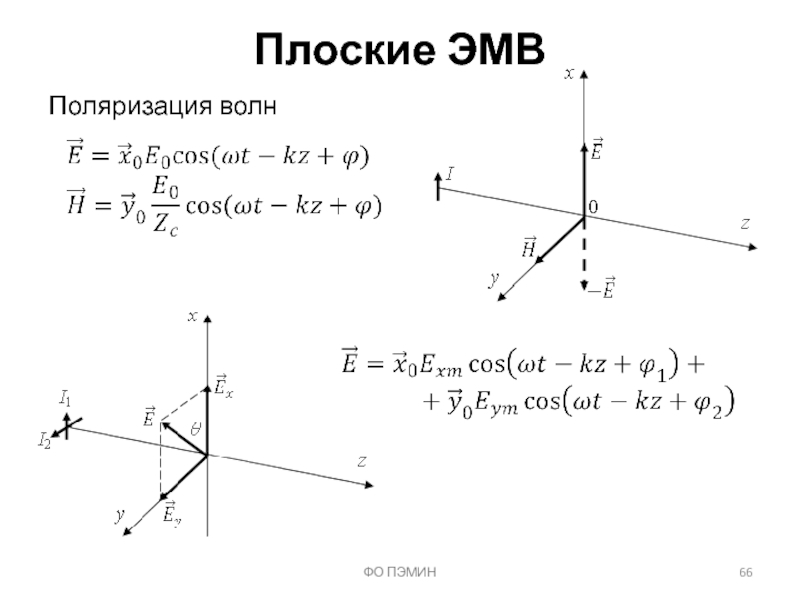
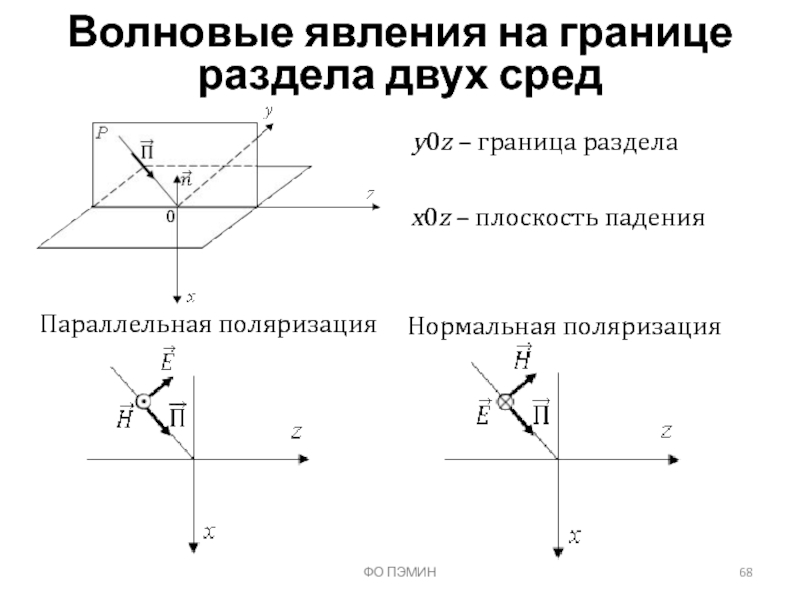
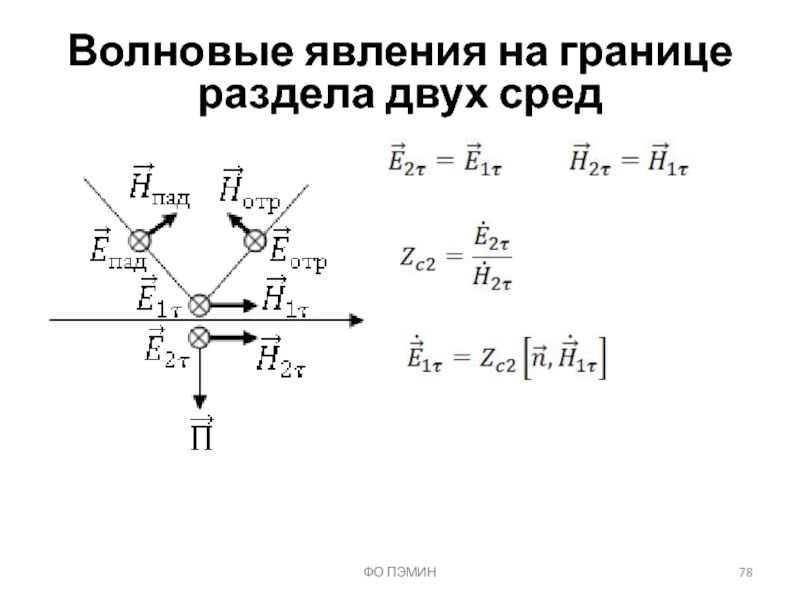
Слайд 68ФО ПЭМИН
Волновые явления на границе раздела двух сред
y0z – граница раздела
Параллельная
Нормальная поляризация
x0z – плоскость падения
Слайд 70ФО ПЭМИН
Волновые явления на границе раздела двух сред
Падение плоской волны на
Нормальная поляризация
Слайд 71ФО ПЭМИН
Волновые явления на границе раздела двух сред
Коэффициенты Френеля
коэффициент отражения:
коэффициент прохождения
Слайд 73ФО ПЭМИН
Волновые явления на границе раздела двух сред
Коэффициенты Френеля
коэффициент отражения:
коэффициент прохождения
Слайд 75ФО ПЭМИН
Волновые явления на границе раздела двух сред
Условие полного прохождения волны
Параллельная поляризация
Нормальная поляризация
Слайд 77ФО ПЭМИН
Волновые явления на границе раздела двух сред
Приближенные граничные условия Леонтовича
Слайд 84ФО ПЭМИН
Поверхностный эффект
Электромагнитный экран
Тонкий экран (медь, f=1 ГГц:
d
Толстый экран. Коэфф.прозрачности определяется, в основном, затуханием во 2-й среде.
Слайд 86ФО ПЭМИН
Постановка задачи дифракции в виде интегрального уравнения
1) Калибр. Лоренца:
2) Использование
Слайд 88ФО ПЭМИН
Постановка задачи дифракции в виде интегрального уравнения
(обобщение ур.-я Поклингтона)
(обобщение ур.-я
- интегралы несобственные
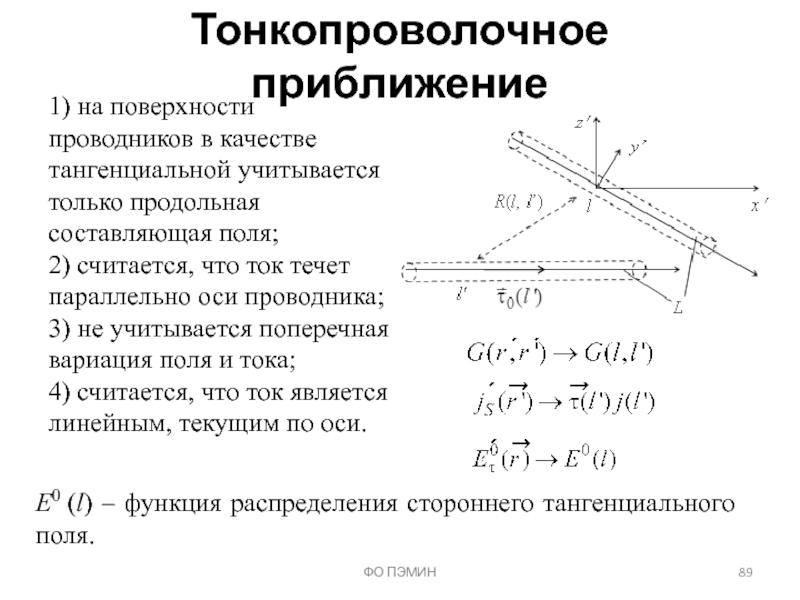
Слайд 89Тонкопроволочное приближение
ФО ПЭМИН
1) на поверхности проводников в качестве тангенциальной учитывается только
2) считается, что ток течет параллельно оси проводника;
3) не учитывается поперечная вариация поля и тока;
4) считается, что ток является линейным, текущим по оси.
E0 (l) – функция распределения стороннего тангенциального поля.
Слайд 90ФО ПЭМИН
Тонкопроволочное приближение
– интегральное уравнение Поклингтона
– интегро-дифференциальное уравнение Харрингтона
Слайд 91ФО ПЭМИН
Тонкопроволочное приближение
(ядра Фредгольмовского типа)
Искомая функция только под знаком интеграла –
Интегральные уравнения Фредгольма 1-го рода
Уравнение: u = A f
Задача корректна по Адамару, если:
- существует решение: ∀u ∃ f = A–1u ;
- решение определяется однозначно;
- задача устойчива:
∀e > 0 ∃ d(e) > 0: ||u1 – u2|| ≤ δ(ε) ⇒ ||f1 – f2||≤ ε
Задача в тонкопроволочном приближении неустойчива!
Слайд 94ФО ПЭМИН
Уравнения Фредгольма 2-го рода
(аналогично – для произвольного возбуждения, для системы
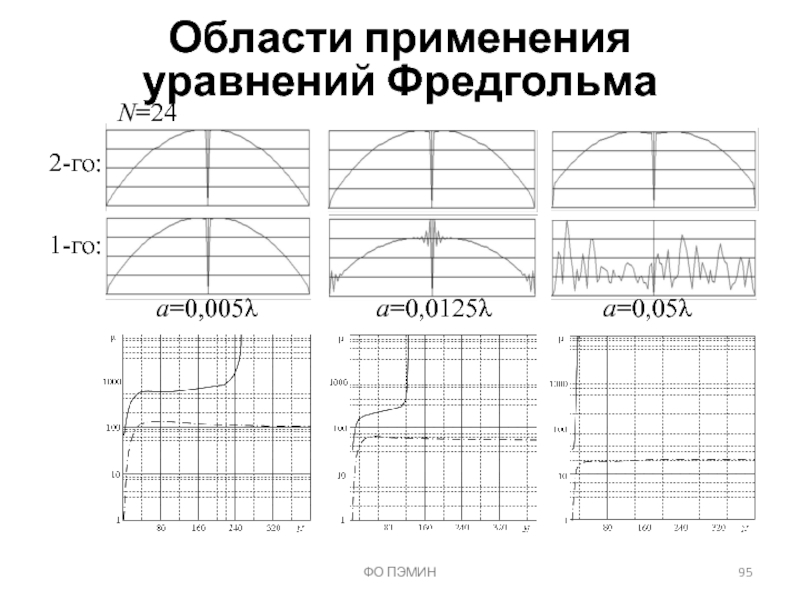
Слайд 96Мера обусловленности μ:
ФО ПЭМИН
Области применения уравнений Фредгольма
где
- норма матрицы [K]
Ограничения на
«Мягкие» ограничения на радиус сверху для ИУ 2-го рода из-за роста погрешности приближения осевого тока.
Устраняется введением поправочной функции, частично компенсирующей погрешность.
Слайд 97Методы решения ИУ
Проекционная схема Бубнова-Галеркина
ФО ПЭМИН
Решаемое ИУ:
Вводим функции
, образующие ортогональный
Ищем приближенное решение в виде:
- искомые коэффициенты
Точное решение:
- невязка
Базисные функции, используемые для разложения невязки,
, называются весовыми или координатными
Невязка должна быть ортогональна всем базисным ф-ям.
Слайд 98ФО ПЭМИН
Методы решения ИУ
Из требования ортогональности следует:
, k=1,…,N.
, k=1,…,N.
Подставляем разложение по
Слайд 99Метод моментов. Проекционные методы
ФО ПЭМИН
Методы решения ИУ
(Базисные ф-ии не обязательно ортогональны.
Для выведенных выше ИУ:
i = 1 … N, j = 1 … N.
в компактной форме: [Z]=[J][E]
Слайд 100ФО ПЭМИН
Методы решения ИУ
Проблема выбора базиса и модели возбуждения
Выбор базиса существенным
Функции должны: быть равномерно ограниченными; быть непрерывными; иметь ограниченные первые производные; иметь нули на концах проводников.
Базисы полной области: на всем протяжении каждого проводника антенны задаются несколько отличных от нуля базисных функций.
Базисы частичных подобластей: каждая базисная функция отлична от нуля только в пределах электрически короткого отрезка (сегмента).
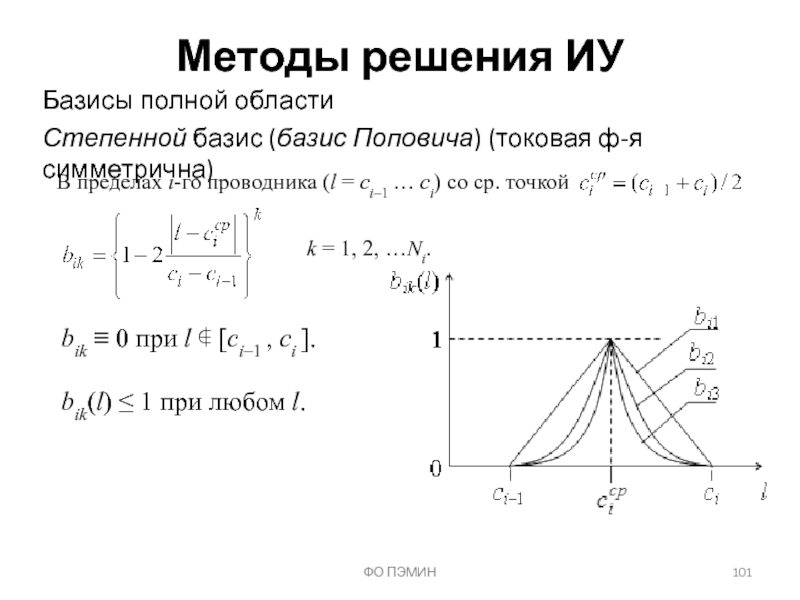
Слайд 101ФО ПЭМИН
Методы решения ИУ
Базисы полной области
Степенной базис (базис Поповича) (токовая ф-я
В пределах i-го проводника (l = ci–1 … ci) со ср. точкой
k = 1, 2, …Ni.
bik ≡ 0 при l ∉ [ci–1 , ci ].
bik(l) ≤ 1 при любом l.
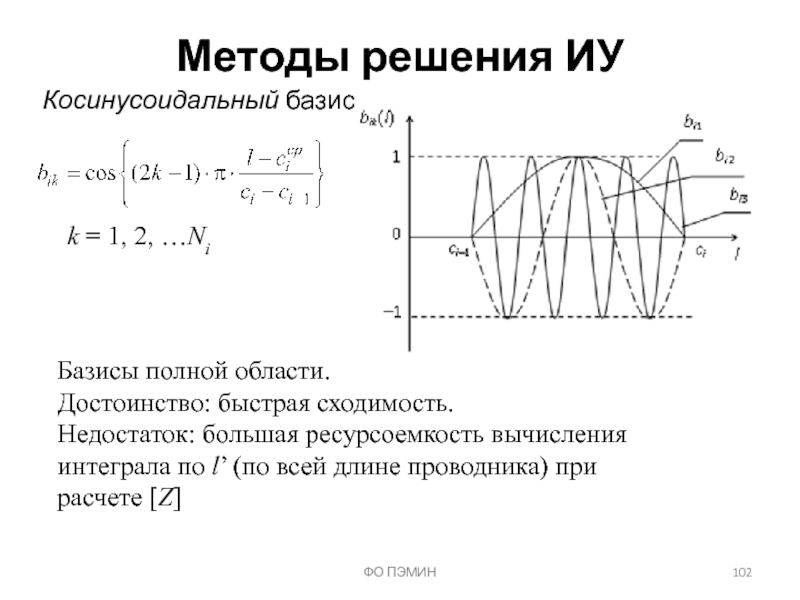
Слайд 102ФО ПЭМИН
Методы решения ИУ
Косинусоидальный базис
k = 1, 2, …Ni
Базисы
Достоинство: быстрая сходимость.
Недостаток: большая ресурсоемкость вычисления интеграла по l’ (по всей длине проводника) при расчете [Z]
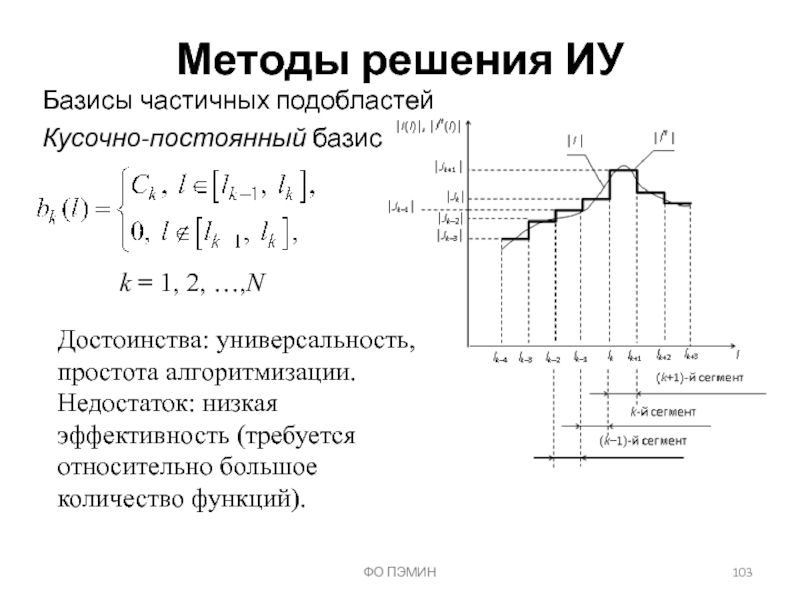
Слайд 103ФО ПЭМИН
Базисы частичных подобластей
Методы решения ИУ
Кусочно-постоянный базис
k = 1, 2,
Достоинства: универсальность, простота алгоритмизации.
Недостаток: низкая эффективность (требуется относительно большое количество функций).
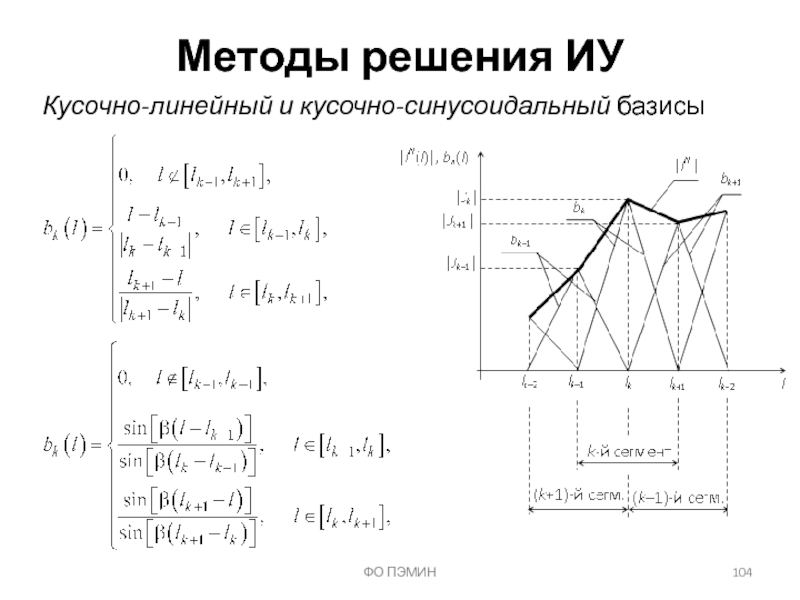
Слайд 105ФО ПЭМИН
Методы решения ИУ
Квазипериодические кусочно-синусоидальные функции (ККФ)
квазипериодическая функция, аппроксимируемая
посредством ККФ (порождающая функция)
M = 1, 3, 5, … – число КФ, использованных для аппроксимации полупериода порождающей функции;
- полупериод порождающей функции
- кусочно-синусоидальные функции (КФ)
Слайд 106ФО ПЭМИН
Методы решения ИУ
Если
ККФ приближает кос. ф-ю
синусоидальную
- любая квазипериодическая ф-я
Слайд 107ФО ПЭМИН
Методы решения ИУ
Центры отрезков – носителей КФ:
Граничные точки полупериодов порождающей
m = 0, 1, 2, … M+1.
γm опр. по критерию совпадения в точках:
m = 1, 2, … M.
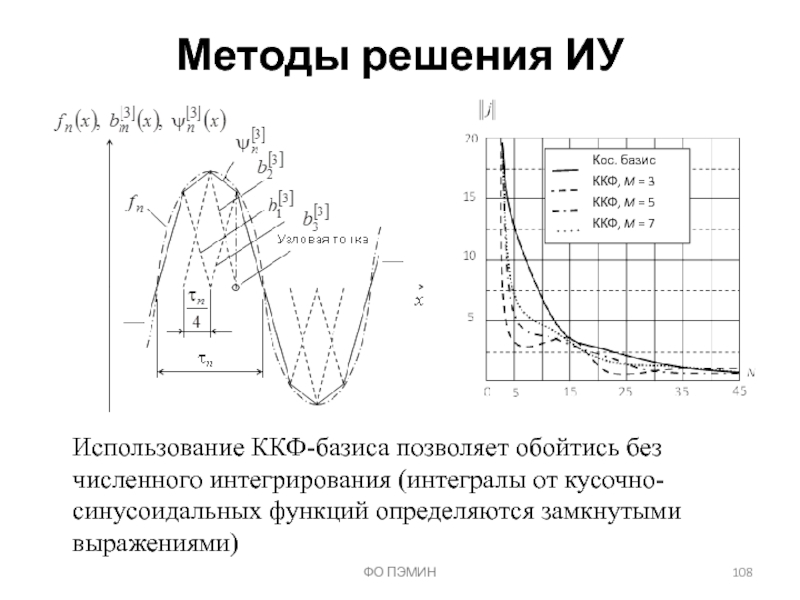
Слайд 108ФО ПЭМИН
Методы решения ИУ
Использование ККФ-базиса позволяет обойтись без
численного интегрирования (интегралы
синусоидальных функций определяются замкнутыми
выражениями)
Слайд 109ФО ПЭМИН
Методы решения ИУ
Формализация сторонних источников (модели возбуждения)
Задание стороннего тока I0
Условие совместимости базиса и модели возбуждения: система функций I0, b1, b2, … bN д.б. ЛНЗ при любом N.
Задание стороннего поля E0
Оно должно порождаться неким током I0:
Условие совместимости, противоположное: базис {bn}, в котором представляется решение j, должен обладать полнотой по отношению к функциям I0
Слайд 110ФО ПЭМИН
Методы решения ИУ
Задание стороннего поля
Задание стороннего тока
При задании ст.
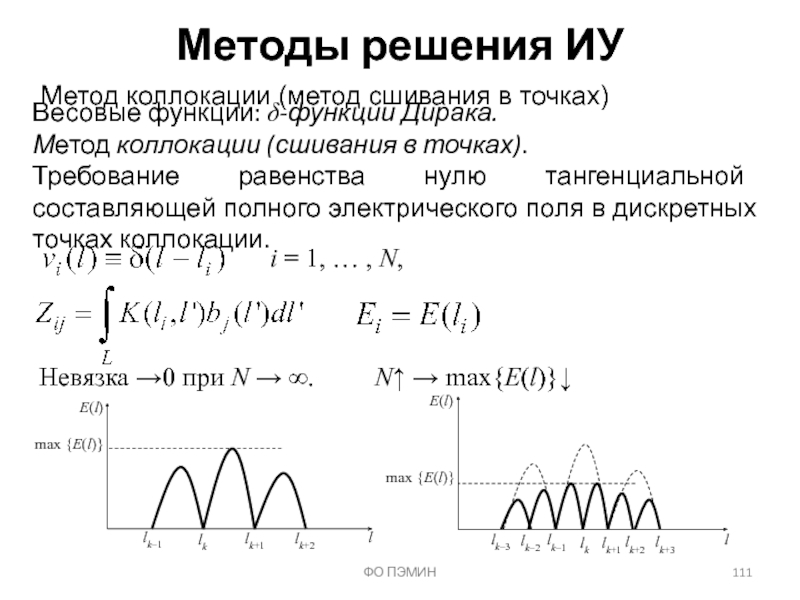
Слайд 111ФО ПЭМИН
Методы решения ИУ
Метод коллокации (метод сшивания в точках)
Весовые функции: δ-функции
Метод коллокации (сшивания в точках).
Требование равенства нулю тангенциальной составляющей полного электрического поля в дискретных точках коллокации.
i = 1, … , N,
Невязка →0 при N → ∞. N↑ → max{E(l)}↓
Слайд 112ФО ПЭМИН
Методы решения ИУ
Метод Галеркина
i = 1, 2, … N.
По сравнению
- из-за необходимости интегрирования по l требуются большие затраты машинного времени на расчет коэффициентов и свободных членов СЛАУ;
- более быстрая сходимость решения, т.е. уменьшение времени на решение СЛАУ.
Выбор opt метода зависит от конкретной задачи.














































































![Мера обусловленности μ:ФО ПЭМИНОбласти применения уравнений Фредгольмагде- норма матрицы [K]Ограничения на радиус сверху для ИУ](/img/tmb/2/182776/1491cbbf33a36fea4fe33ca10df9194f-800x.jpg)