- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многократное рассеяние волн презентация
Содержание
- 1. Многократное рассеяние волн
- 2. Волны в случайно-неоднородных средах Не существует методов
- 3. Функция Грина Поле G(r,r') является случайной функцией,
- 4. Среднее поле что позволяет усреднить полученное волновое уравнение Представим решение в виде ряда Neumann:
- 5. Уравнение для среднего поля Эффективный прием анализа
- 6. Диаграммы Feynmann Диаграммы, получаемые из слабосвязанной при
- 7. Уравнение Dyson Q(r1, r2) - ядро массового
- 8. Оператор Dyson Для определения распространения сигнала оптического
- 9. Уравнение Bethe-Salpeter Получить решение уравнения Bethe-Salpeter в
- 10. Лучевое приближение Эффективные неоднородности, внутри когерентное распрос-транение
- 11. Решение уравнение Dyson для квазиоднородного поля k1
- 12. Локализация ядер Проведем почленную замену переменных
- 13. Замена переменных Последнее уравнение подобно уравнению распространения когерентности в свободном пространстве
- 14. Уравнение переноса излучения (УПИ) УПИ является следствие уравнений Maxwell в лучевом приближении
Слайд 1Многократное рассеяние волн
?: +7 (495) 763-5239 BudakVP@mpei.ru
Будак Владимир Павлович,
Национальный исследовательский университет «МЭИ»
кафедра
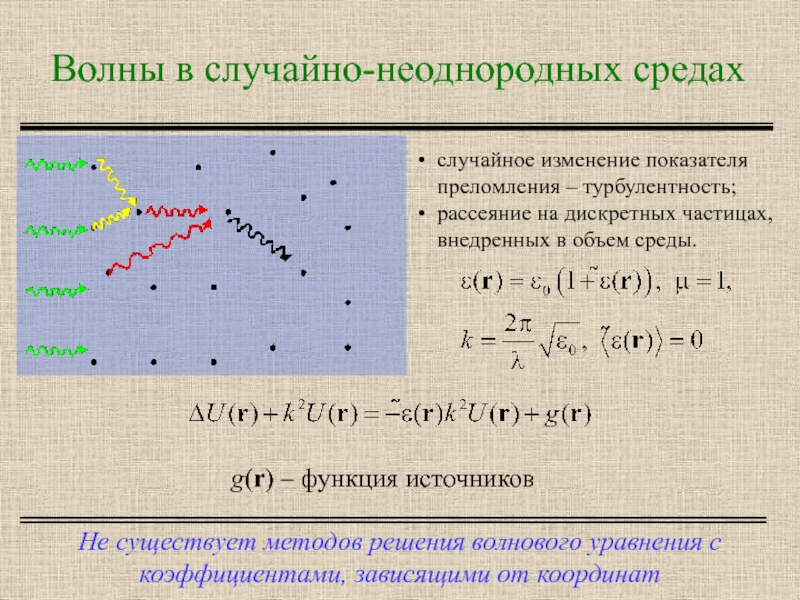
Слайд 2Волны в случайно-неоднородных средах
Не существует методов решения волнового уравнения с коэффициентами,
случайное изменение показателя преломления – турбулентность;
рассеяние на дискретных частицах, внедренных в объем среды.
g(r) – функция источников
Слайд 3Функция Грина
Поле G(r,r') является случайной функцией, статистически связанной с флуктуациями среды
Предполагая
Полученное уравнение можно решать, используя функцию Грина свободного пространства G0(r,r'):
Слайд 4Среднее поле
что позволяет усреднить полученное волновое уравнение
Представим решение в виде ряда
Слайд 5Уравнение для среднего поля
Эффективный прием анализа подобных рядов, основан на геометрическом
Ряд состоит из нескольких групп подобных членов, однако их приведение представляет значительный аналитические трудности
Слайд 6Диаграммы Feynmann
Диаграммы, получаемые из слабосвязанной при разрыве линии G0, могут оказаться
Отберем из ряда все сильно связанные диаграммы. Поскольку все они начинаются и заканчиваются линией G0, то сумму всех сильно связанных диаграмм можно обозначить
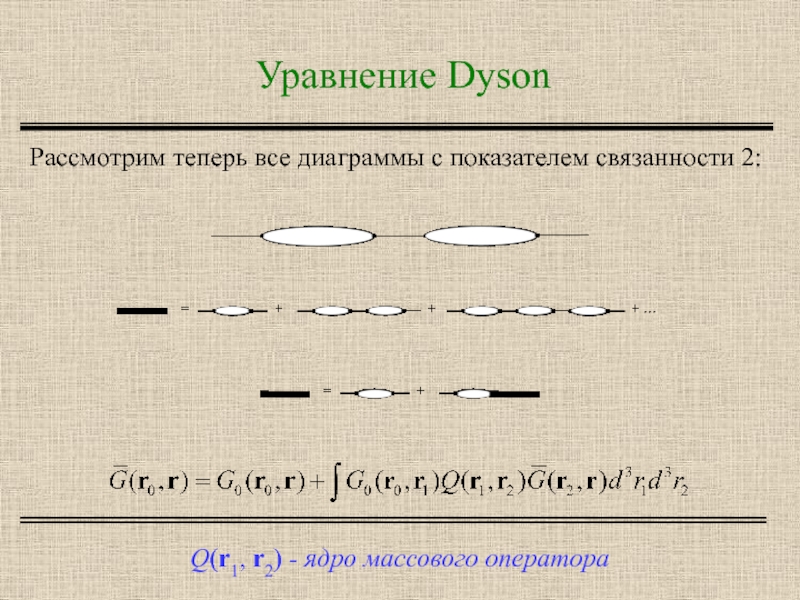
Слайд 7Уравнение Dyson
Q(r1, r2) - ядро массового оператора
Рассмотрим теперь все диаграммы с
Слайд 8Оператор Dyson
Для определения распространения сигнала оптического приемника необходимо знать функцию распространения
Удобно представить уравнение Dyson в форме близкой волновому уравнению - подействуем на обе части уравнения оператором (Δ+k2) и учтем
Слайд 9Уравнение Bethe-Salpeter
Получить решение уравнения Bethe-Salpeter
в общем случае не удается
Подействуем дважды на
Слайд 10Лучевое приближение
Эффективные неоднородности, внутри когерентное распрос-транение (Fresnel), а друг друга облучают
одногрупповые – соответствуют одной однородности, быстро убывают с ростом ρ;
многогрупповые – относятся к различным неоднородностям, связаны волновым облучением, убывают медленно с ростом ρ
Слайд 11Решение уравнение Dyson
для квазиоднородного поля
k1 = Rekэф > k - увеличение
k2 = Imkэф > 0 - уменьшение среднего поля или перекачка энергии из когерентной компоненты поля в некогерентное