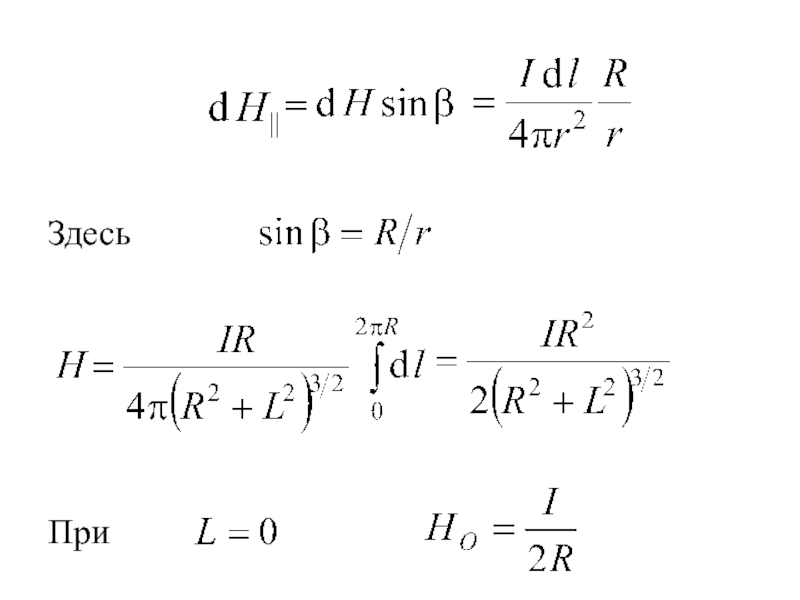- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Магнитные явления презентация
Содержание
- 1. Магнитные явления
- 2. Магнитное поле Вектор индукции магнитного поля
- 3. Экспериментальный закон, определяющий поле точечного заряда, движущегося
- 4. В вакууме – вектор
- 5. Магнитное поле неоднородное переменное
- 6. Закон Био-Савара Найдем магнитное поле, создаваемое
- 7. Если ток течет по тонкому проводу с
- 8. (5.4) → (5.3): (5.5) (5.3) и (5.5) – закон Био-Савара (Био-Савара-Лапласа).
- 9. Принцип суперпозиции магнитных полей (из
- 10. Из (5.3) и (5.5) с учетом (5.6)
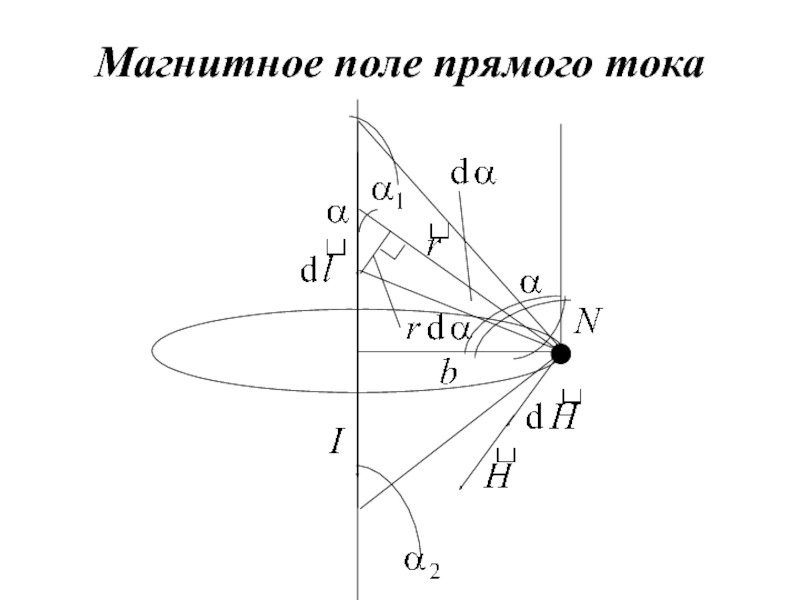
- 11. Магнитное поле прямого тока
- 12. Из закона Био-Савара где Тогда где
- 13. Напряженность магнитного поля прямого тока
- 14. Магнитное поле кругового тока
- 15. Здесь При
- 16. Теорема о циркуляции вектора индукции магнитного поля
- 17. При непрерывном распределении токов в пространстве, охватываемом
- 18. Применим теорему Стокса: Стягивая контур
- 19. на длину контура или участка контура, теорему
- 20. Вспомогательный контур совпадает с силовой линией магнитного
- 21. Зададим направление обхода по контуру, совпадающее с
- 22. (Расчет магнитного поля тороида и соленоида)
Слайд 1Лекция № 5
МАГНИТНОЕ ПОЛЕ
В ВАКУУМЕ
Лекция № 5-6
МАГНИТНЫЕ ЯВЛЕНИЯ
Литература: Иродов И.Е.
Слайд 2 Магнитное поле
Вектор индукции магнитного поля
– вектор магнитной индукции, в СИ
порождается движущимися зарядами (токами).
действует на движущийся электрический заряд и не действует на покоящийся заряд.
Слайд 3 Экспериментальный закон, определяющий поле точечного заряда, движущегося с постоянной нерелятивистской скоростью
где
(5.1)
Гн/м – магнитная постоянная
– радиус-вектор, проведенный от заряда к точке наблюдения.
Слайд 4
В вакууме
– вектор напряженности магнитного поля в вакууме, в СИ
(5.2)
касателен к этой линии.
Силовая линия – линия, в каждой точке которой
Уравнение силовой линии
Слайд 5 Магнитное поле
неоднородное
переменное во времени
Магнитное поле – вихревое
статическое (постоянное во времени)
однородное
Слайд 6Закон Био-Савара
Найдем магнитное поле, создаваемое постоянными электрическими токами
Подставим в
где dV – элементарный объем, ρ – объемная плотность заряда.
– плотность тока. Тогда
Слайд 7 Если ток течет по тонкому проводу с площадью поперечного сечения ΔS,
(5.3)
где dl – элемент длины провода.
Введем
в направлении тока I.
Тогда
(5.4)
и
– объемный и линейный элементы тока соответственно.
Слайд 9Принцип суперпозиции
магнитных полей
(из опыта): магнитное поле, создаваемое несколькими токами
(5.6)
Слайд 10Из (5.3) и (5.5) с учетом (5.6)
считается положительным).
(5.7)
где l
Если проводящее тело нельзя считать тонким проводником, то, используя (5.4), получим
ток I
где V − объем тела, в котором текут токи.
(5.8)
Слайд 13
Напряженность магнитного поля прямого тока
Для бесконечно длинного проводника
Тогда магнитное
Слайд 16Теорема о циркуляции вектора индукции магнитного поля
в интегральной форме: циркуляция вектора
(5.9)
Слайд 17 При непрерывном распределении токов в пространстве, охватываемом контуром, циркуляция вектора магнитной
через произвольную поверхность S, натянутую на этот контур
(5.10)
Здесь направления обхода контура и нормали
к поверхности S связаны между собой правилом правого винта.
Слайд 18
Применим теорему Стокса:
Стягивая контур к точке, получим теорему о циркуляции
(5.11)
Физический смысл теоремы о циркуляции: магнитное поле неконсервативное (5.9), (5.10) и вихревое (5.11).
Слайд 19на длину контура или участка контура, теорему о циркуляции удобно применять
Если можно подобрать такой произвольный замкнутый контур, что интеграл в левой части (5.9) и (5.10) сводится к умножению
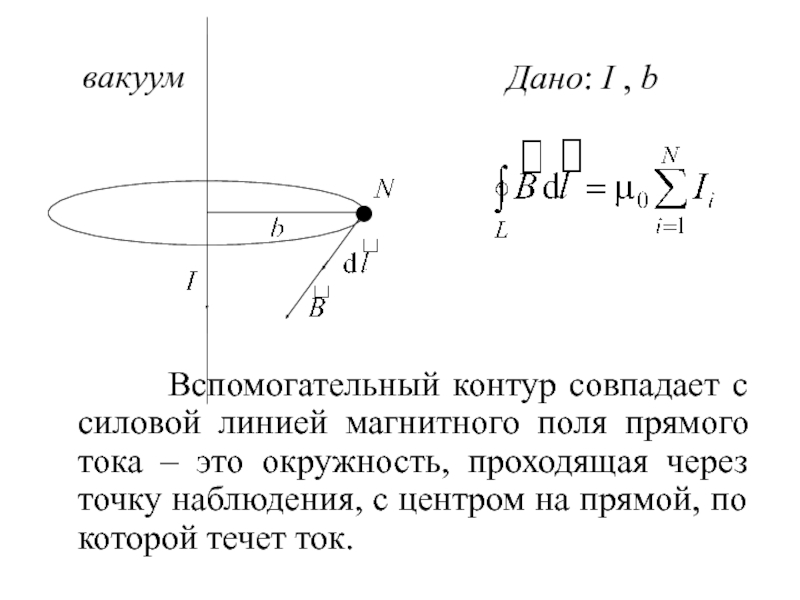
Слайд 20 Вспомогательный контур совпадает с силовой линией магнитного поля прямого тока –
Дано: I , b
вакуум
Слайд 21Зададим направление обхода по контуру, совпадающее с направлением
Тогда
На всем вспомогательном
Тогда

![Магнитное поле Вектор индукции магнитного поля – вектор магнитной индукции, в СИ B = [Тл] (тесла),](/img/tmb/5/436437/eeb3b394b49ad1d72bde23250bb951ea-800x.jpg)

![В вакууме – вектор напряженности магнитного поля в вакууме, в СИ H = [А/м]. (5.2)касателен](/img/tmb/5/436437/125b8d8c0784e18b1b1607591281f045-800x.jpg)