- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод замены нескольких последовательно соединенных генераторов напряжения одним эквивалентным. (Лекция 4) презентация
Содержание
- 1. Метод замены нескольких последовательно соединенных генераторов напряжения одним эквивалентным. (Лекция 4)
- 2. Метод замены нескольких последовательно соединенных генераторов напряжения одним эквивалентным
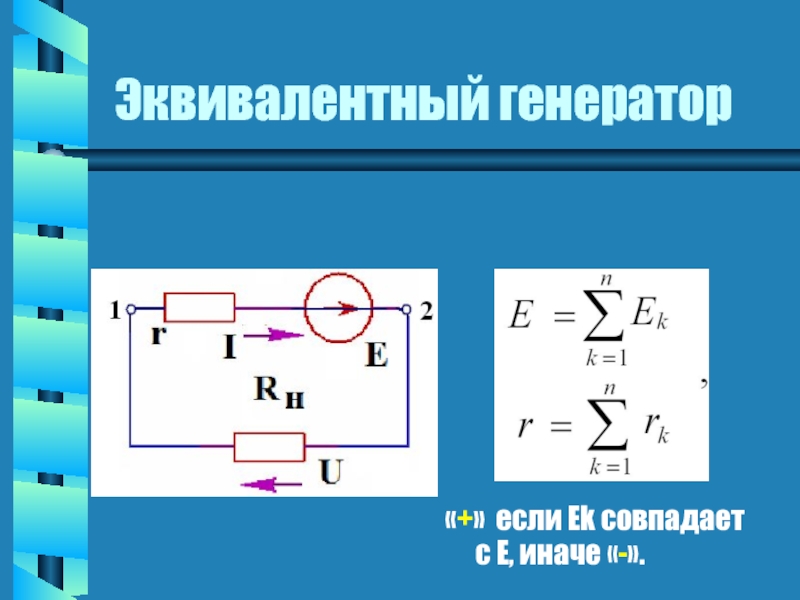
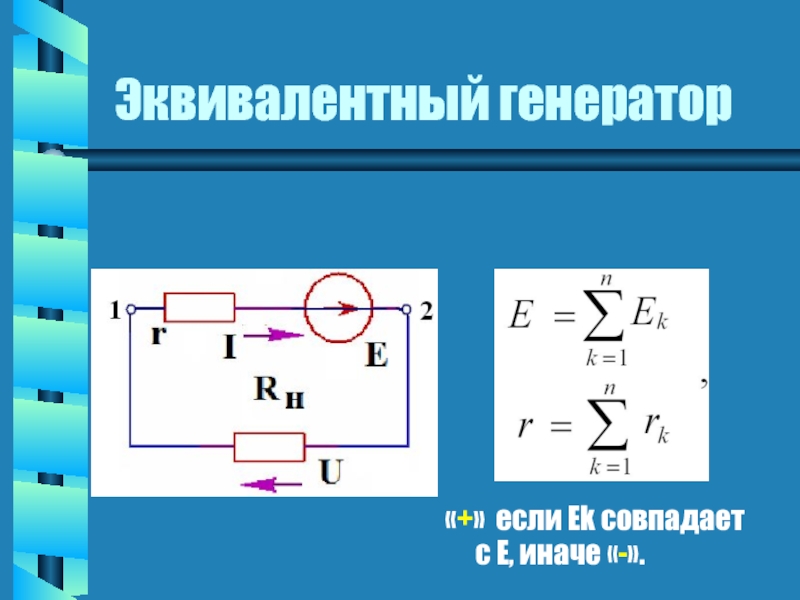
- 3. Эквивалентный генератор «+» если Еk совпадает с Е, иначе «-».
- 4. Метод замены нескольких последовательно соединенных генераторов напряжения одним эквивалентным
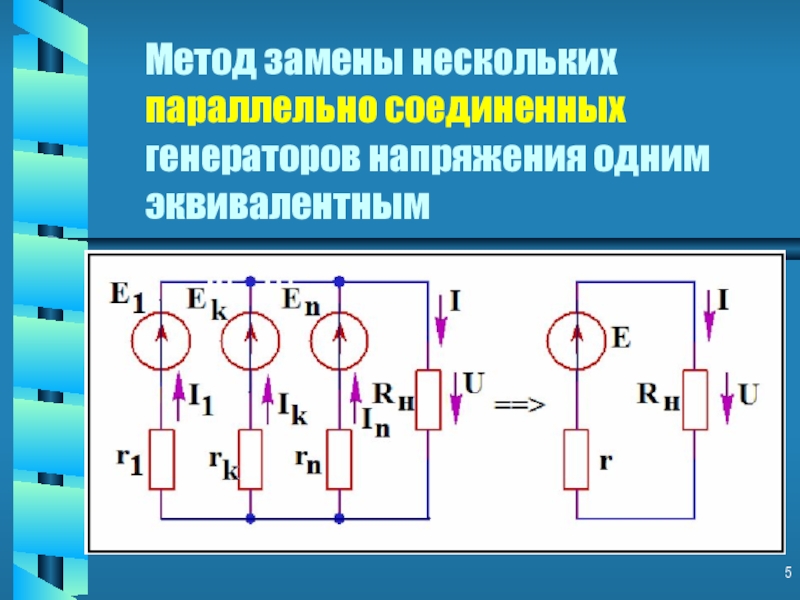
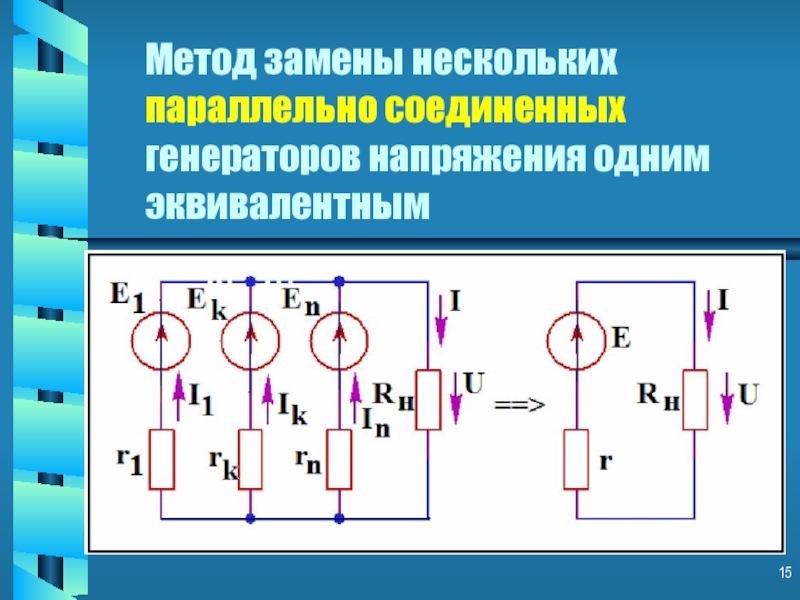
- 5. Метод замены нескольких параллельно соединенных генераторов напряжения одним эквивалентным
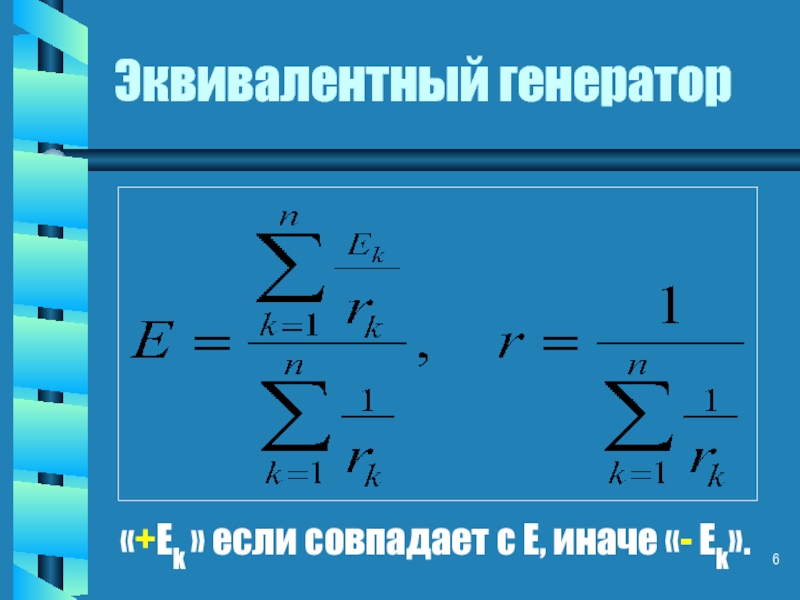
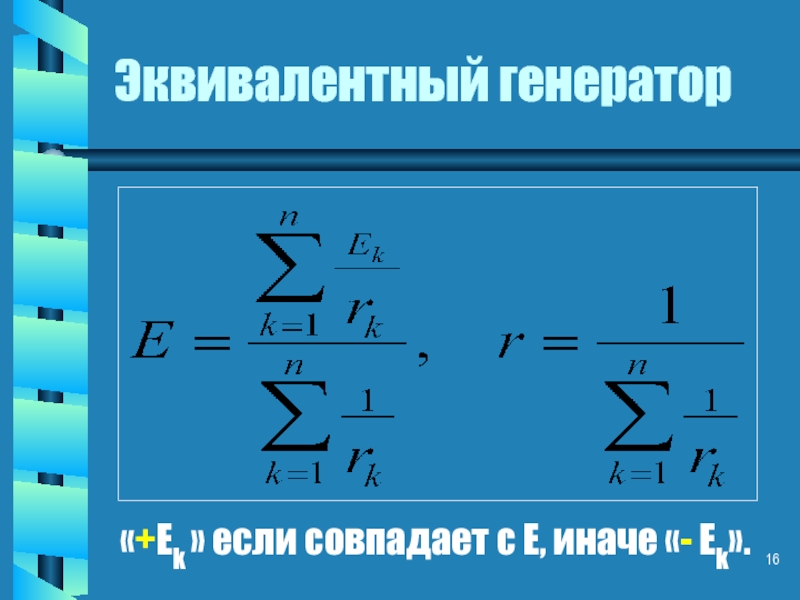
- 6. Эквивалентный генератор «+Еk » если совпадает с Е, иначе «- Еk».
- 7. Ток в нагрузке Rн
- 8. Ток в k-ой ветви (k=1, 2,…, n)
- 9. Пример. Определить показания вольтметра, сопротивление которого бесконечно
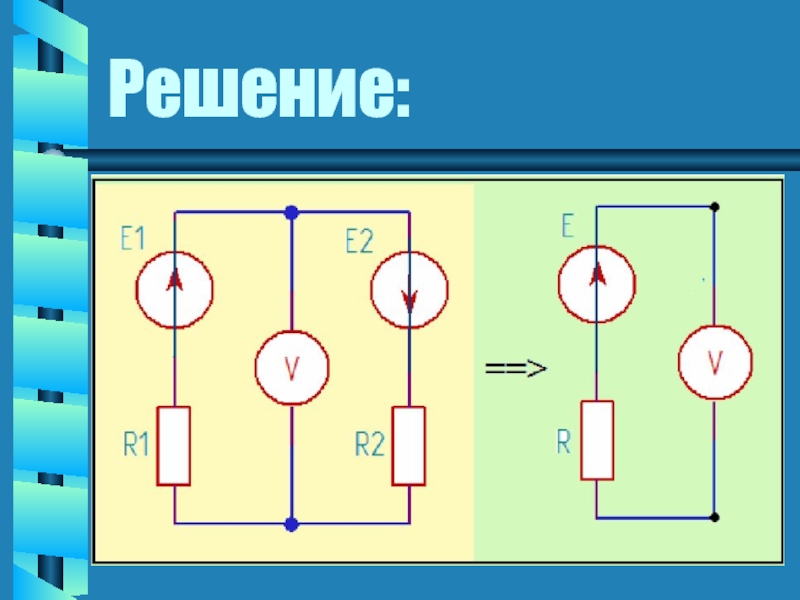
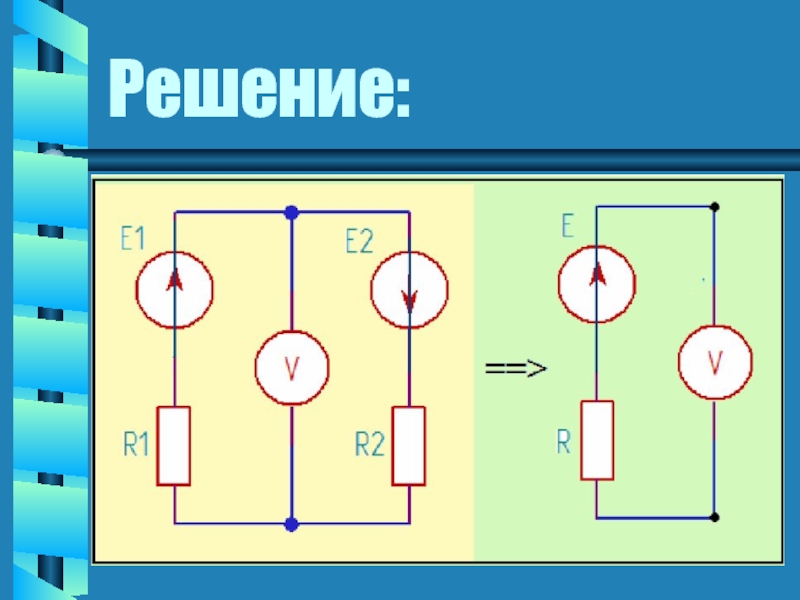
- 10. Решение:
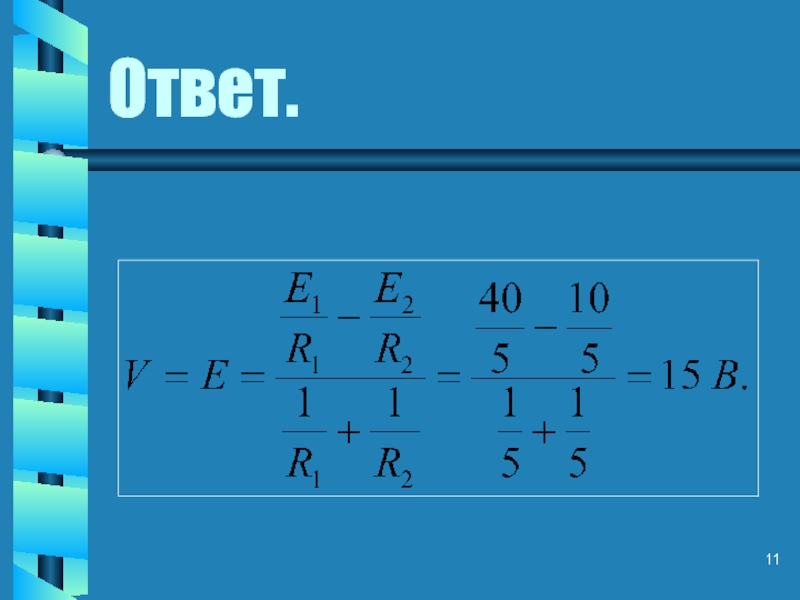
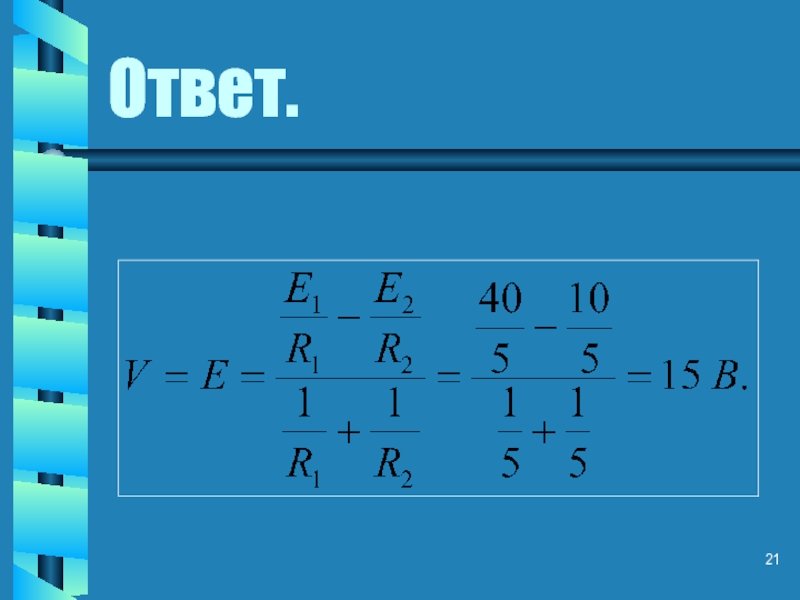
- 11. Ответ.
- 12. Метод замены нескольких последовательно соединенных генераторов напряжения одним эквивалентным
- 13. Эквивалентный генератор «+» если Еk совпадает с Е, иначе «-».
- 14. Метод замены нескольких последовательно соединенных генераторов напряжения одним эквивалентным
- 15. Метод замены нескольких параллельно соединенных генераторов напряжения одним эквивалентным
- 16. Эквивалентный генератор «+Еk » если совпадает с Е, иначе «- Еk».
- 17. Ток в нагрузке Rн
- 18. Ток в k-ой ветви (k=1, 2,…, n)
- 19. Пример. Определить показания вольтметра, сопротивление которого бесконечно
- 20. Решение:
- 21. Ответ.
- 22. Метод замены нескольких параллельно соединенных генераторов тока
- 23. Источник с ЭДС Е и внутренним сопротивлением
- 24. Основные методы расчета электрических цепей
- 25. 1. Метод расчета с помощью законов Кирхгофа
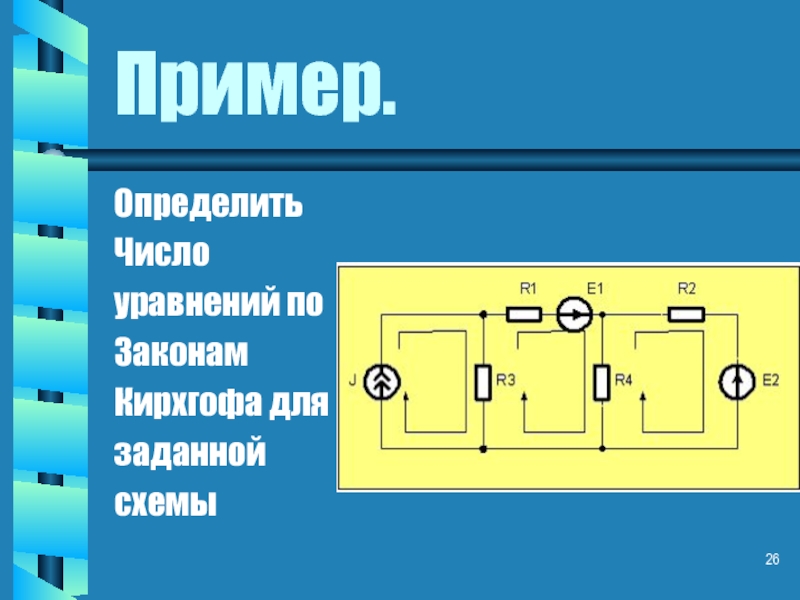
- 26. Пример. Определить Число уравнений по Законам Кирхгофа для заданной схемы
- 27. Решение: Число ветвей: Число узлов: Число источников тока: Общее число уравнений:
- 28. 2. Метод узловых потенциалов Метод узловых
- 29. Составление уравнений по методу узловых потенциалов
- 30. Система уравнений
- 31. Символы системы уравнений Gkk— сумма проводимостей всех
- 32. Символы системы уравнений — алгебраическая сумма произведений
- 33. Символы системы уравнений — алгебраическая сумма токов
- 34. Замечание Если в схеме некоторые узлы соединяются
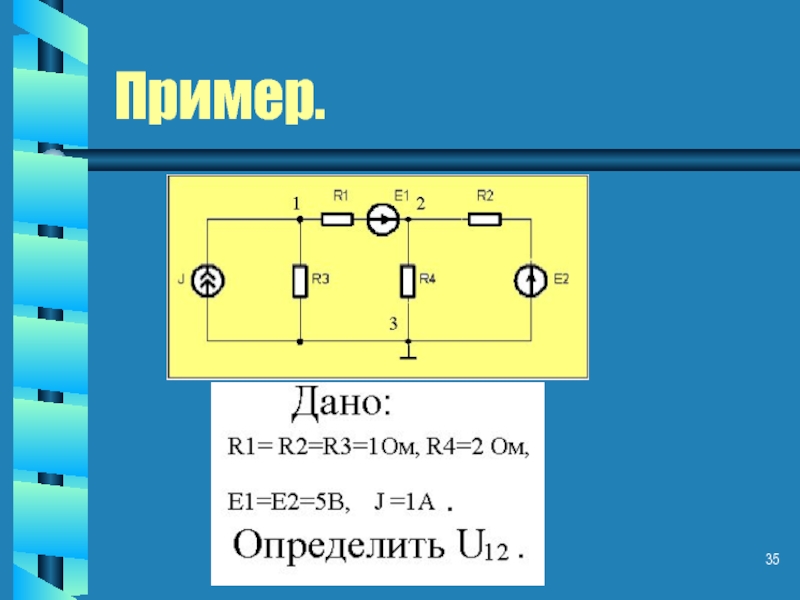
- 35. Пример.
- 36. Решение: Система уравнений V1(G1+G2 )
- 37. 3. Метод контурных токов базируется на
- 38. Составление уравнений по методу контурных токов Вначале
- 39. Составление уравнений по методу контурных токов
- 40. Система уравнений
- 41. Символы системы уравнений где Rnn— собственное сопротивление
- 42. Символы системы уравнений Enn— алгебраическая сумма
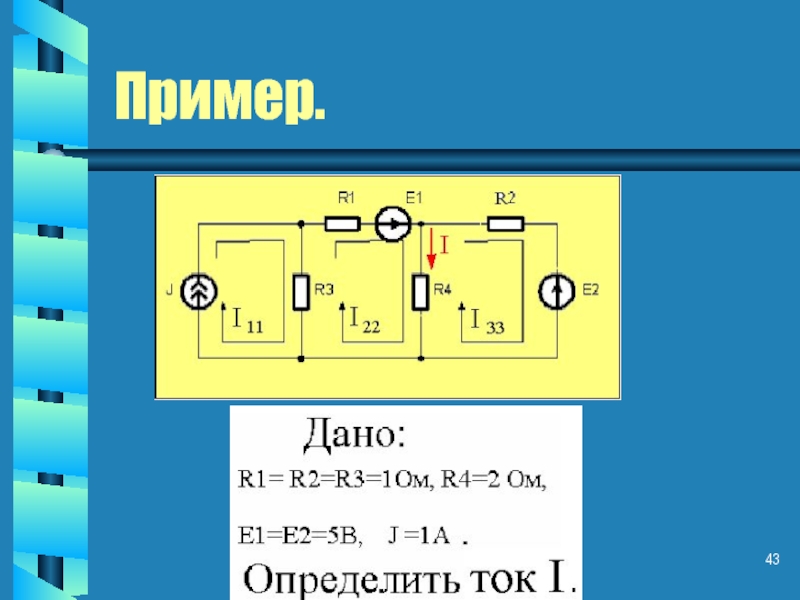
- 43. Пример.
- 44. Решение: Система уравнений (R1+R3+R4) I22- R4 I33
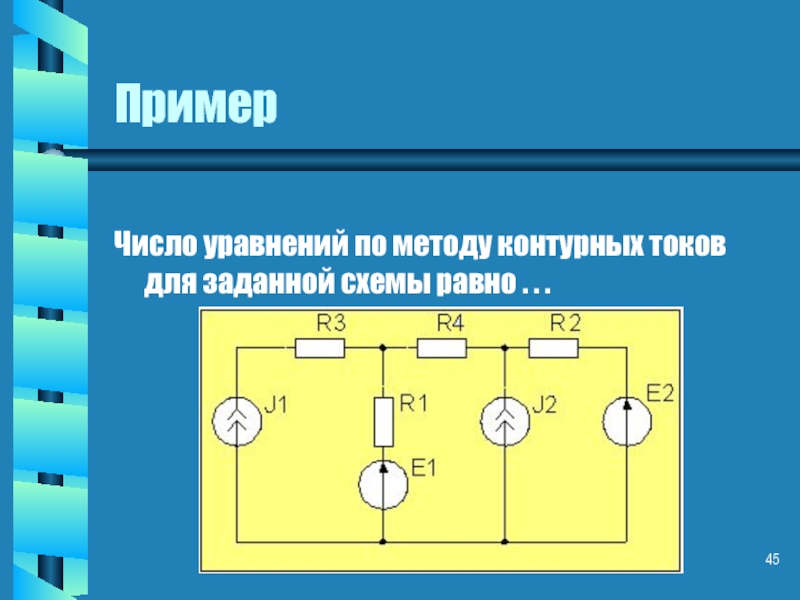
- 45. Пример Число уравнений по методу
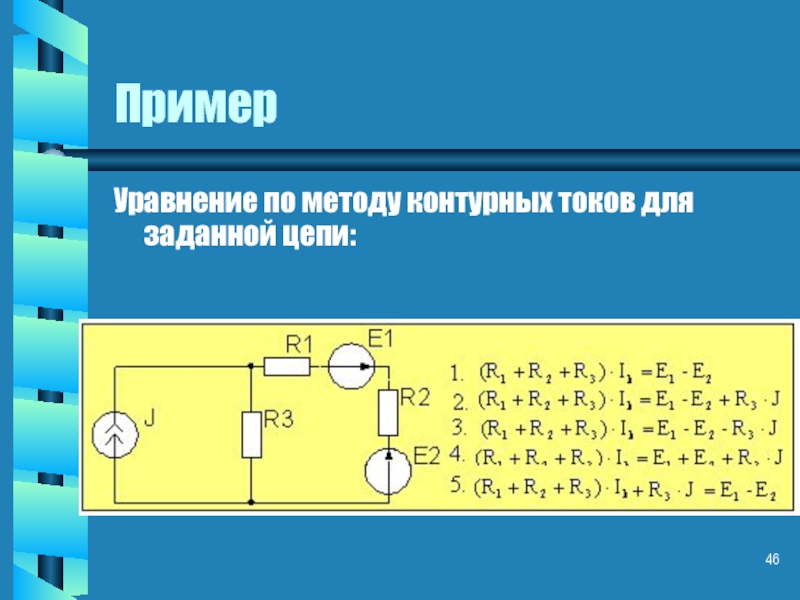
- 46. Пример Уравнение по методу контурных токов для заданной цепи:
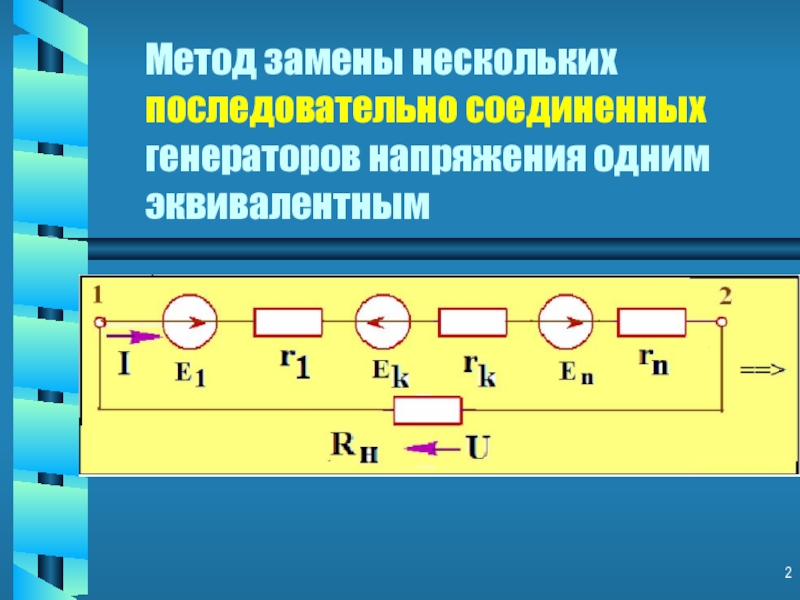
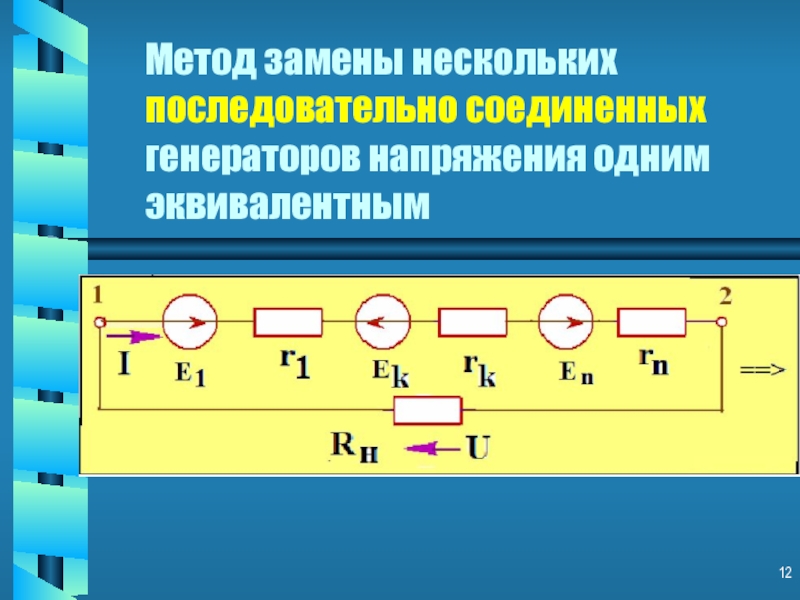
Слайд 2Метод замены нескольких последовательно соединенных генераторов напряжения одним эквивалентным
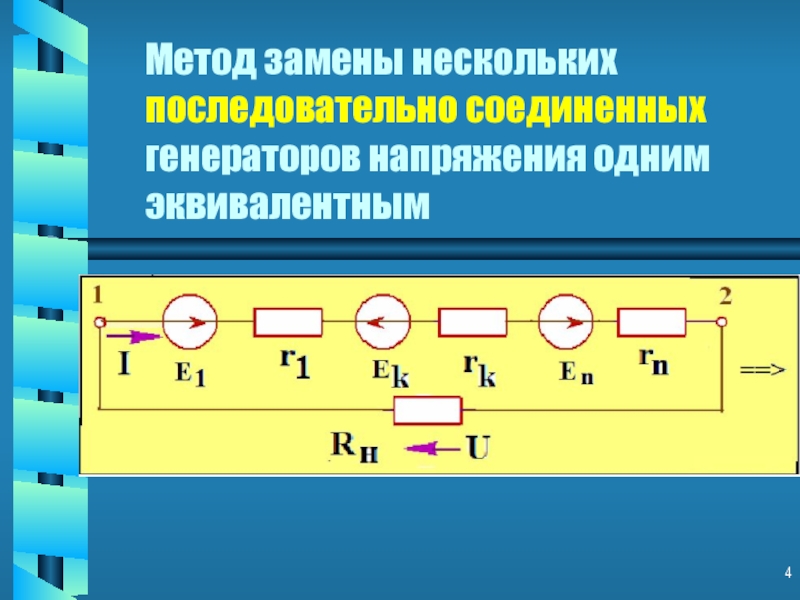
Слайд 4Метод замены нескольких последовательно соединенных генераторов напряжения одним эквивалентным
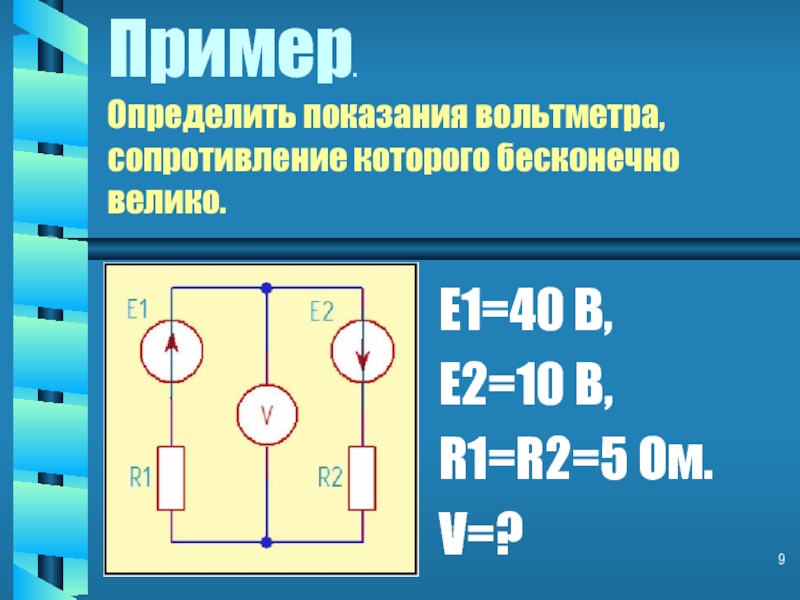
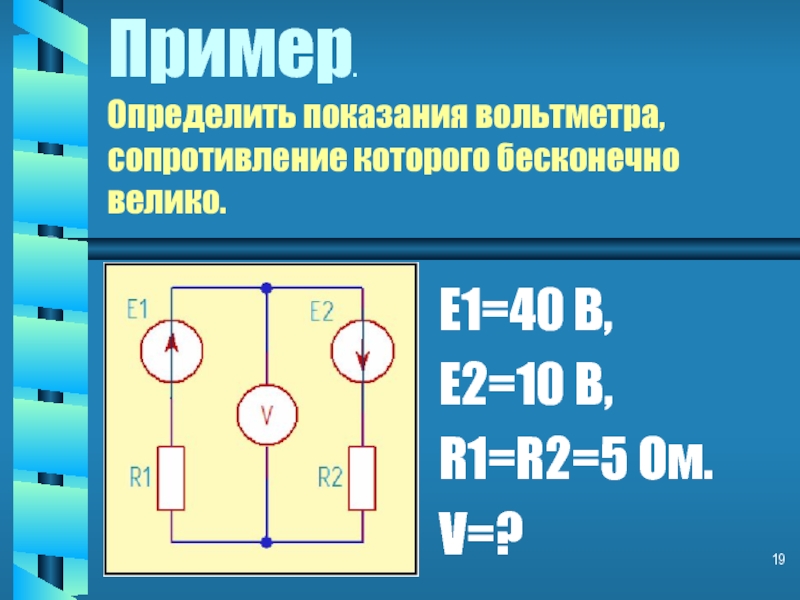
Слайд 9Пример.
Определить показания вольтметра, сопротивление которого бесконечно велико.
E1=40 B,
E2=10 B,
R1=R2=5 Ом.
V=?
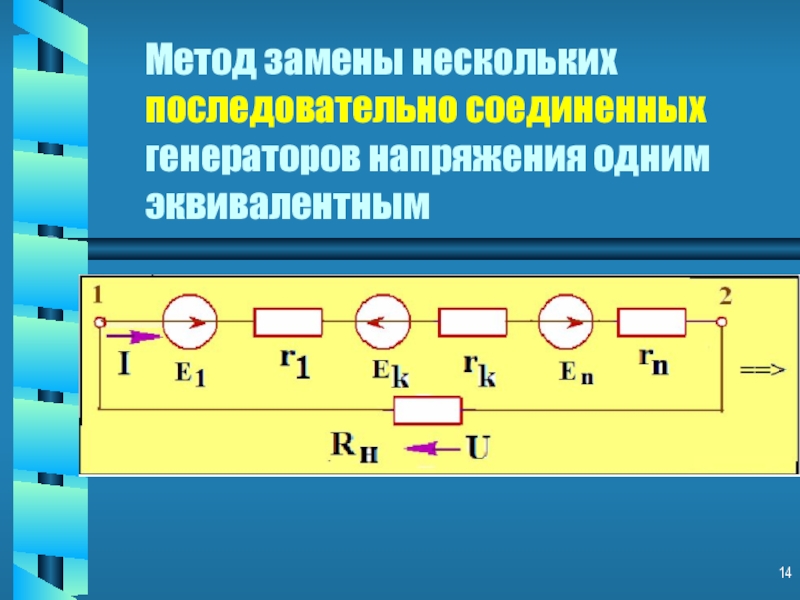
Слайд 12Метод замены нескольких последовательно соединенных генераторов напряжения одним эквивалентным
Слайд 14Метод замены нескольких последовательно соединенных генераторов напряжения одним эквивалентным
Слайд 19Пример.
Определить показания вольтметра, сопротивление которого бесконечно велико.
E1=40 B,
E2=10 B,
R1=R2=5 Ом.
V=?
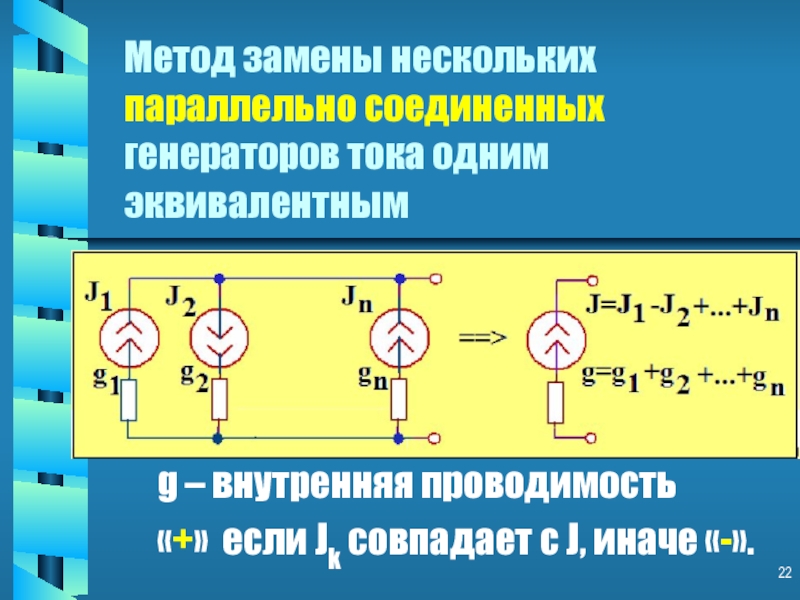
Слайд 22Метод замены нескольких параллельно соединенных генераторов тока одним эквивалентным
g – внутренняя
проводимость
«+» если Jk совпадает с J, иначе «-».
«+» если Jk совпадает с J, иначе «-».
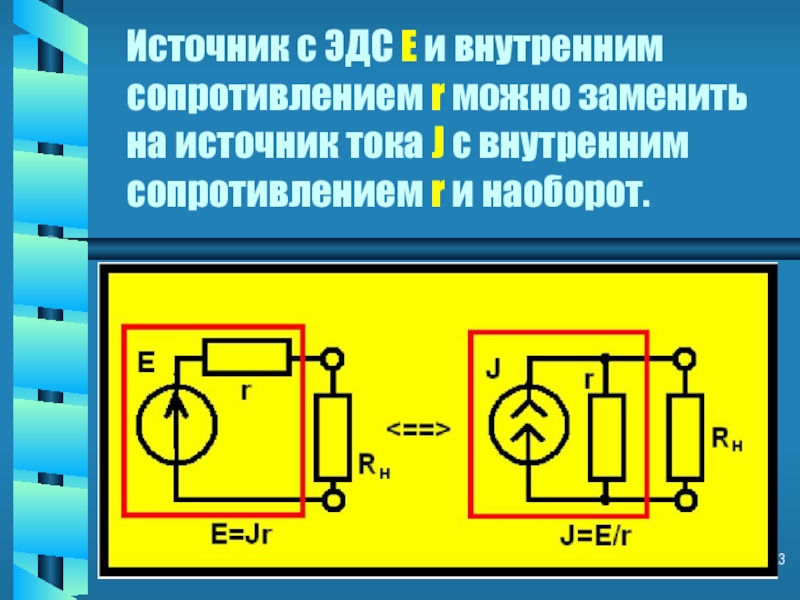
Слайд 23Источник с ЭДС Е и внутренним сопротивлением r можно заменить на
источник тока J с внутренним сопротивлением r и наоборот.
Слайд 251. Метод расчета с помощью законов Кирхгофа
Общее число
независимых
уравнений,
составляемых по
первому и
второму законам
Кирхгофа:
Слайд 282. Метод узловых потенциалов
Метод узловых потенциалов базируется на первом законе
КирхгофаМетод узловых потенциалов базируется на первом законе Кирхгофа и законе Ома.
Позволяет уменьшить количество независимых уравнений системы до числа, равного количеству узлов без одного:
Позволяет уменьшить количество независимых уравнений системы до числа, равного количеству узлов без одного:
Слайд 29Составление уравнений по методу узловых потенциалов
Вначале полагают равным нулю потенциал
какого-либо узла.
Для определения потенциалов (напряжений) оставшихся (Nу -1) узлов составляется следующая система уравнений:
Для определения потенциалов (напряжений) оставшихся (Nу -1) узлов составляется следующая система уравнений:
Слайд 31Символы системы уравнений
Gkk— сумма проводимостей всех
ветвей, подсоединенных к узлу k
(собственная проводимость
узла k );
Gkm — сумма проводимостей всех
ветвей, непосредственно соединяющих
узел k с узлом m (взаимная проводимость
узлов k и m );
Gkm — сумма проводимостей всех
ветвей, непосредственно соединяющих
узел k с узлом m (взаимная проводимость
узлов k и m );
Слайд 32Символы системы уравнений
— алгебраическая сумма произведений ЭДС ветвей, подсоединенных к узлу
k, на проводимости этих ветвей ( со знаком плюс берутся ЭДС, которые направлены к узлу k , и со знаком минус — от узла k);
Слайд 33Символы системы уравнений
— алгебраическая сумма токов источников тока, подсоединенных к узлу
k (со знаком плюс берутся токи, которые направлены к узлу k, а со знаком минус — от узла k ).
Слайд 34Замечание
Если в схеме некоторые узлы
соединяются идеальными источниками
ЭДС, то число уравнений, составляемых
по
методу узловых потенциалов,
уменьшается до ( NУ -1 - NЕ) ,
где NЕ — число ветвей, содержащих только идеальные источники ЭДС.
уменьшается до ( NУ -1 - NЕ) ,
где NЕ — число ветвей, содержащих только идеальные источники ЭДС.
Слайд 36Решение:
Система уравнений
V1(G1+G2 ) – V2G1 = - E1G1+J,
- V1G1+V2(G1+G2+G4)
= E1G1+E2G2, где ( G=1/R ).
1. V1(1+1) – V2 1= - 5+1, 2 V1 – V2 = - 4,
V1 1+V2(1+1+0,5) = 5+5. - V1+2,5 V2= 10.
2. V1 = 0 В; V2 = 4 В.
3. U12=V1-V2= - 4 В.
1. V1(1+1) – V2 1= - 5+1, 2 V1 – V2 = - 4,
V1 1+V2(1+1+0,5) = 5+5. - V1+2,5 V2= 10.
2. V1 = 0 В; V2 = 4 В.
3. U12=V1-V2= - 4 В.
Слайд 373. Метод контурных токов
базируется на втором законе Кирхгофабазируется на втором
законе Кирхгофа и законе Ома.
Позволяет уменьшить количество
независимых уравнений системы до
числа .
Позволяет уменьшить количество
независимых уравнений системы до
числа .
Слайд 38Составление уравнений по методу контурных токов
Вначале обозначают условные контурные токи,
протекающие в
каждом контуре цепи (по любой
ветви цепи должен проходить хотя бы один
выбранный контурный ток).
Ток в любой ветви цепи можно представить в
виде алгебраической суммы контурных токов,
протекающих по этой ветви.
ветви цепи должен проходить хотя бы один
выбранный контурный ток).
Ток в любой ветви цепи можно представить в
виде алгебраической суммы контурных токов,
протекающих по этой ветви.
Слайд 39Составление уравнений по методу контурных токов
Необходимо выбирать контурные токи
источников тока (Nт) так, чтобы каждый из них проходил только через один источник (эти контурные токи совпадают с соответствующими токами источников тока и они являются заданными условиями задачи). Оставшиеся контурные токи выбирают проходящими по ветвям, не содержащим идеальных источников тока. Для них составляется следующая система уравнений:
Слайд 41Символы системы уравнений
где Rnn— собственное сопротивление контура n (сумма сопротивлений всех
ветвей, входящих в контур n); Rnl— общее сопротивление контуров n и l, причем Rnl = Rln : если направления контурных токов в общей ветви для контуров n и l совпадают, то сопротивление положительно, в противном случае отрицательно.
Слайд 42Символы системы уравнений
Enn— алгебраическая сумма ЭДС, входящих в контур n
, знак положителен, если эдс направлена по контурному току; Rn— общее сопротивление ветви контура n с контуром, содержащим источник тока J : если направления контурных токов и токов источников в общей ветви совпадают, то Rn положительно, в противном случае отрицательно.
Слайд 44Решение:
Система уравнений
(R1+R3+R4) I22- R4 I33 – R3 J =E1 ,
-R4 I22+(R2+
R4) I33 = -E2 .
1. 4 I22- 2 I33-1 =5, 2. I33 = - 1 A , I22= 1 A .
- 2 I22 + 3 I33 = - 5.
3. I = I22- I33= 2 A .
1. 4 I22- 2 I33-1 =5, 2. I33 = - 1 A , I22= 1 A .
- 2 I22 + 3 I33 = - 5.
3. I = I22- I33= 2 A .