- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы статики презентация
Содержание
- 1. Элементы статики
- 2. В общем случае, когда тело может двигаться
- 3. Особым случаем равновесия является равновесие тела на
- 4. Механические колебания 1. Свободные механические колебания. 1.1.
- 5. 1. Свободные механические колебания Линейный гармонический
- 6. 1.1. Пружинный маятник Уравнение основного закона динамики
- 7. Собственная циклическая (круговая) частота зависит
- 8. 1.2. Физический маятник Динамика физического маятника:
- 9. Дифференциальное уравнение собственных колебаний физического маятника:
- 10. Поэтому
- 11. 1.3. Математический маятник Математический маятник –
- 12. 1.4. Графическое представление колебаний Для произвольных
- 13. 2. Затухающие колебания Второй закон Ньютона
- 14. График затухающих колебаний β < ω0 –
- 15. Параметры затухающих колебаний Коэффициент затухания β
- 16. 3. Вынужденные колебания Вынужденными колебаниями называются
- 17. В колебательной системе одновременно происходят два процесса:
- 18. Если ω → 0, то
- 19. Добротность колебательной системы, находящейся в режиме вынужденных
Слайд 1Лекция 8
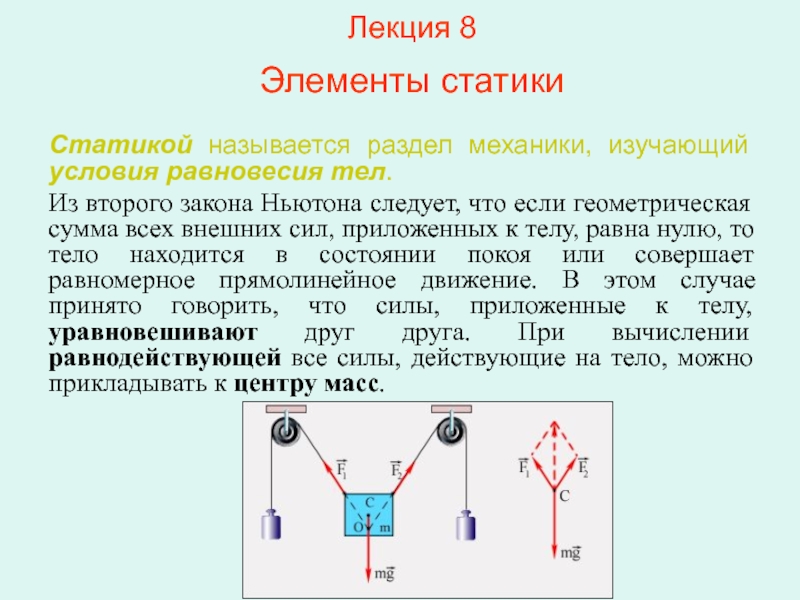
Элементы статики
Статикой называется раздел механики, изучающий условия равновесия
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс.
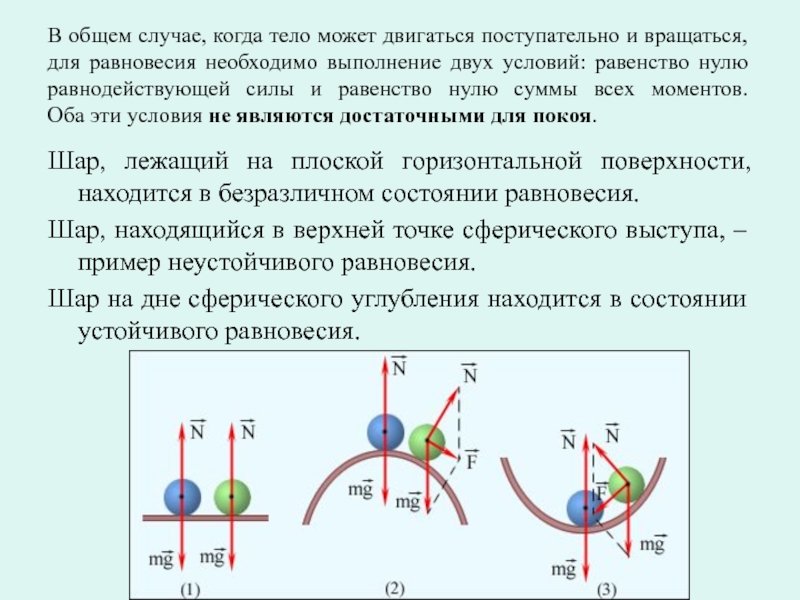
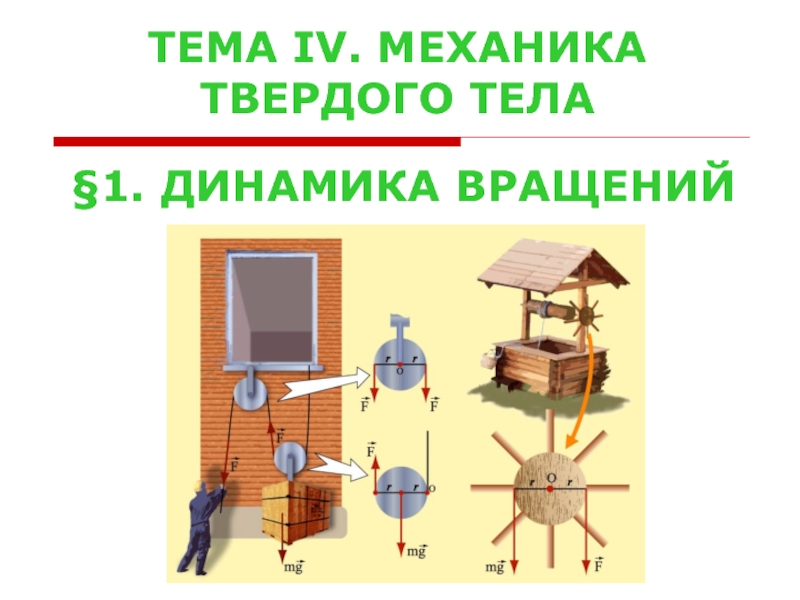
Слайд 2В общем случае, когда тело может двигаться поступательно и вращаться, для
Шар, лежащий на плоской горизонтальной поверхности, находится в безразличном состоянии равновесия.
Шар, находящийся в верхней точке сферического выступа, – пример неустойчивого равновесия.
Шар на дне сферического углубления находится в состоянии устойчивого равновесия.
Слайд 3Особым случаем равновесия является равновесие тела на опоре.
Тело находится в
Слайд 4Механические колебания
1. Свободные механические колебания.
1.1. Пружинный маятник
1.2. Физический маятник
1.3.Математический маятник
1.4. Графическое
2.Затухающие колебания
3. Вынужденные колебания
Слайд 51. Свободные механические колебания
Линейный гармонический осциллятор – колебательная система, совершающая
Примеры линейных гармонических осцилляторов
Пружинный маятник – материальная точка массой m, подвешенная на пружине жесткостью k.
Физический маятник – абсолютно твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции.
Математический маятник – материальная точка, подвешенная на невесомой и нерастяжимой нити длиной l.
Гармонические колебания линейного гармонического осциллятора можно представить так: вторая производная от смещения по времени должна быть прямо пропорциональна величине смещения из положения равновесия
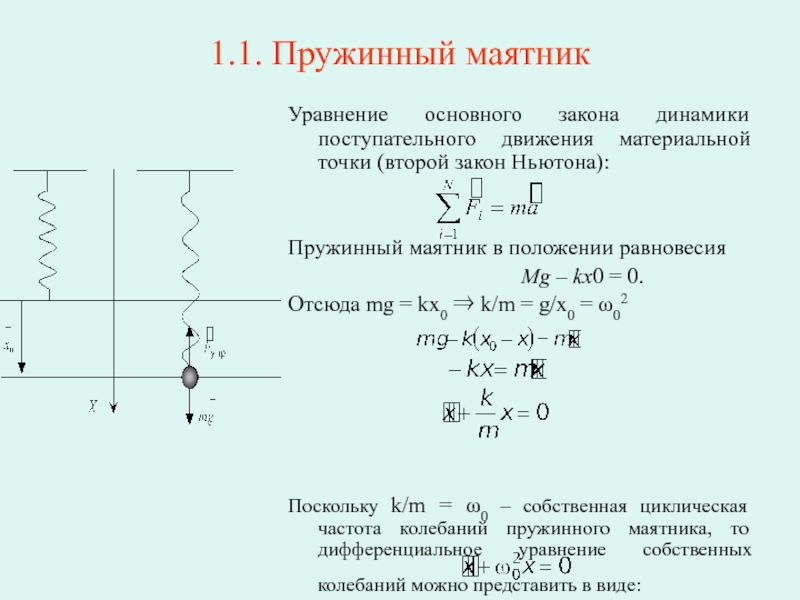
Слайд 61.1. Пружинный маятник
Уравнение основного закона динамики поступательного движения материальной точки (второй
Пружинный маятник в положении равновесия
Mg – kx0 = 0.
Отсюда mg = kx0 ⇒ k/m = g/x0 = ω02
Поскольку k/m = ω0 – собственная циклическая частота колебаний пружинного маятника, то дифференциальное уравнение собственных колебаний можно представить в виде:
Слайд 7Собственная циклическая (круговая) частота
зависит от параметров колебательной системы:
Если в начальный
Период собственных колебаний: T0.
Линейная частота: ν0.
Фаза колебания: Ф = ω0t + φ определяет значение смещения х в данный момент времени, где ϕ – начальная фаза колебания.
Уравнение гармонических колебаний пружинного маятника:
Слайд 81.2. Физический маятник
Динамика физического маятника: ◉M – вектор момента силы
Уравнение основного закона динамики вращательного движения абсолютно твердого тела:
При малых углах sinθ ≈ θ (в радианах). Тогда:
Слайд 9Дифференциальное уравнение собственных колебаний физического маятника:
Поскольку
ℑ – момент инерции маятника относительно точки О,
h – высота, на которую поднимается центр инерции (точка С), определяется по формуле:
здесь lф = ОС – длина физического маятника, а - hm максимальная высота подъема центра инерции.
При малых θ sinθ ≈ θ (в радианах) и тогда
Слайд 10Поэтому
где θ - мгновенное значение угла отклонения маятника от положения равновесия, а θm - максимальное значение этого угла.
Уравнение гармонических колебаний физического маятника:
Амплитуда θm определяется начальным запасом энергии и не зависит от параметров колебательной системы.
Собственная циклическая (круговая) частота
зависит от параметров колебательной системы:
Период собственных колебаний: T0.
Линейная частота: ν0.
Фаза колебания: Ф = ω0t + φ определяет значение смещения в данный момент времени.
Уравнение гармонических колебаний физического маятника:
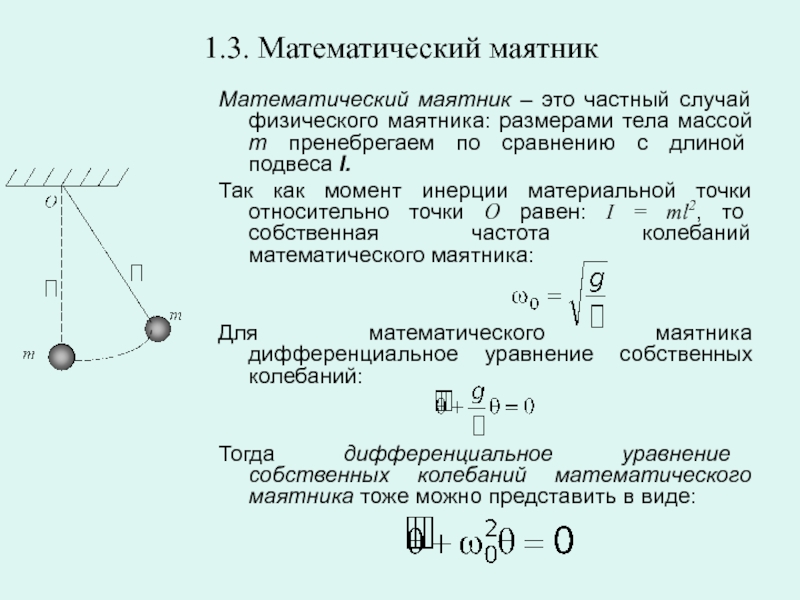
Слайд 111.3. Математический маятник
Математический маятник – это частный случай физического маятника:
Так как момент инерции материальной точки относительно точки О равен: I = ml2, то собственная частота колебаний математического маятника:
Для математического маятника дифференциальное уравнение собственных колебаний:
Тогда дифференциальное уравнение собственных колебаний математического маятника тоже можно представить в виде:
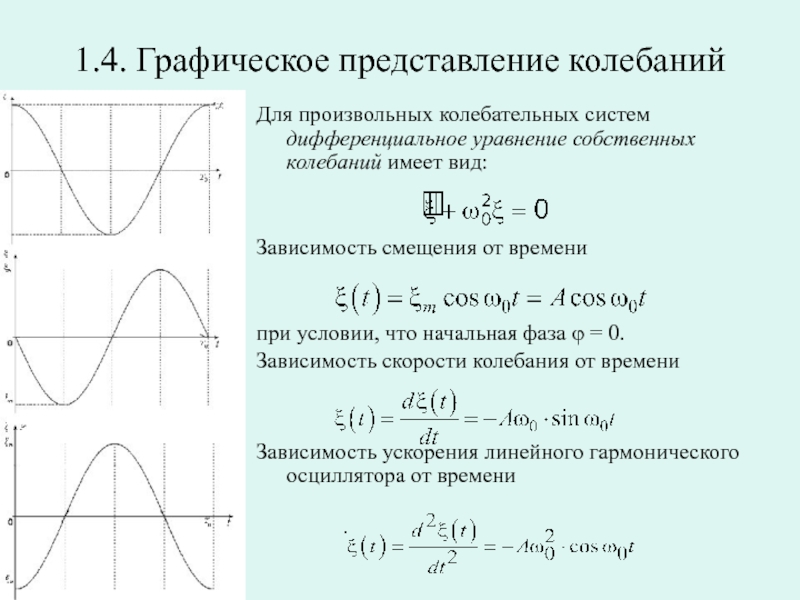
Слайд 121.4. Графическое представление колебаний
Для произвольных колебательных систем дифференциальное уравнение собственных
Зависимость смещения от времени
при условии, что начальная фаза φ = 0.
Зависимость скорости колебания от времени
Зависимость ускорения линейного гармонического осциллятора от времени
Слайд 132. Затухающие колебания
Второй закон Ньютона для пружинного маятника в вязкой
где – сила вязкого трения; r – коэффициент трения.
Тогда дифференциальное уравнение затухающих колебаний пружинного маятника:
или
Здесь β = r/2m – коэффициент затухания.
Для произвольных колебательных систем дифференциальное уравнение затухающих колебаний имеет вид:
,
а его решение
,
где
– частота затухающих колебаний; T ′ – период затухающих колебаний.
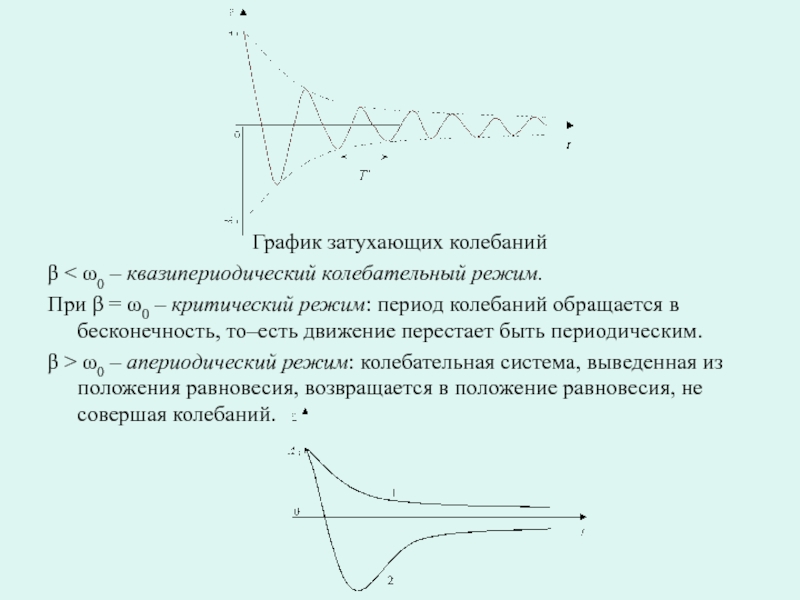
Слайд 14График затухающих колебаний
β < ω0 – квазипериодический колебательный режим.
При β =
β > ω0 – апериодический режим: колебательная система, выведенная из положения равновесия, возвращается в положение равновесия, не совершая колебаний.
Слайд 15Параметры затухающих колебаний
Коэффициент затухания β
Если за некоторое время τe амплитуда
,
то
.
Тогда , а, следовательно, ,
где τe – время релаксации.
Логарифмический декремент затухания λ
Логарифмический декремент равен натуральному логарифму отношения амплитуд соседних колебаний, то есть отличающихся на один период T ′:
Физический смысл логарифмического декремента λ – величина, обратная числу колебаний, в течение которых амплитуда убывает в e раз:
Слайд 163. Вынужденные колебания
Вынужденными колебаниями называются колебания, происходящие под действием внешней
В соответствии со вторым законом Ньютона: ,
,
где – внешняя периодическая сила, действующая на пружинный маятник.
В скалярном виде:
.
Дифференциальное уравнение вынужденных колебаний пружинного маятника:
можно представить в виде
,
где – приведенная сила.
Слайд 17В колебательной системе одновременно происходят два процесса:
1. Затухающие колебания x1(t);
2. Незатухающие
Решение дифференциального уравнения вынужденных колебаний представим в виде суммы двух решений x = x1 + x2:
Общее решение однородного уравнения затухающих колебаний:
,
где – циклическая частота затухающих колебаний.
Уравнение справедливо, если
и при ω < ω0 и
и при ω > ω0.
Резонансом называют явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний (ω → ω0).
Функция A(ω) достигает экстремума при частоте вынуждающей силы ω, равной
, здесь ωрез – резонансная частота.
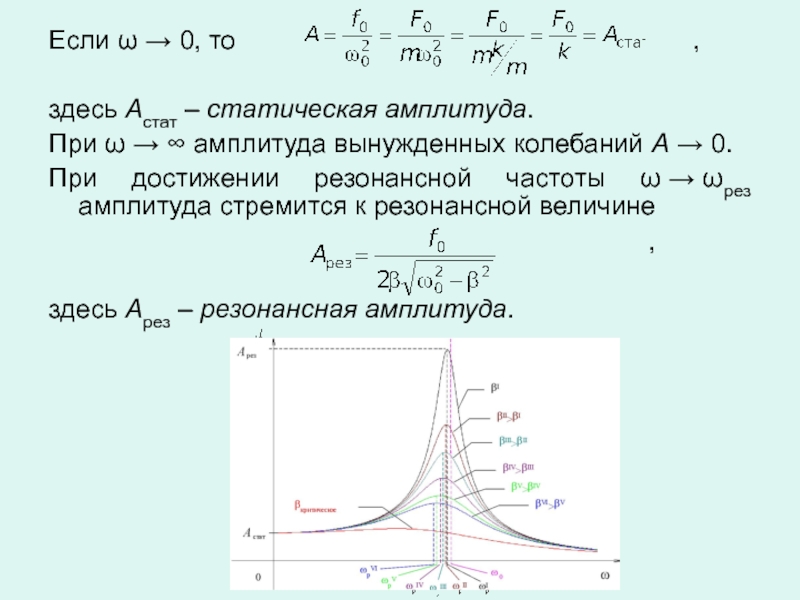
Слайд 18Если ω → 0, то
здесь Aстат – статическая амплитуда.
При ω → ∞ амплитуда вынужденных колебаний A → 0.
При достижении резонансной частоты ω → ωрез амплитуда стремится к резонансной величине
,
здесь Aрез – резонансная амплитуда.
Слайд 19Добротность колебательной системы, находящейся в режиме вынужденных колебаний, можно найти как
Добротность Q определяется как величина, обратно пропорциональная логарифмическому декременту затухания:
.
При слабом затухании добротность можно представить как
,
где Е0 – запасенная энергия; ΔE – потери энергии за один период.
Добротность можно представить и как отношение резонансной амплитуды к статической, т.е. как коэффициент усиления:
.
При слабом затухании добротность равна
.