- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задача 3. Что нужно для стального статически неопределимого ступенчатого стержня круглого поперечного сечения? презентация
Содержание
- 1. Задача 3. Что нужно для стального статически неопределимого ступенчатого стержня круглого поперечного сечения?
- 2. Задача № 3 Для стального статически неопределимого
- 3. Решение: В заделках возникают реактивные моменты ТА
- 4. Для составления уравнения перемещений отбросим правую заделку,
- 5. Применяя принцип независимости действия сил, запишем уравнение
- 6. Для упрощения вычислений выразим Jp1 = πd14
- 7. Эпюру крутящих моментов строим, начиная с левого
- 8. Строим эпюру касательных напряжений, пользуясь формулой
- 9. Опасным оказалось поперечное сечение участка ВЕ. Таким
- 10. В пределах каждого из участков бруса эпюра
- 11. Аналогично вычисляются углы поворота остальных граничных
Слайд 2Задача № 3
Для стального статически неопределимого ступенчатого стержня круглого поперечного сечения
требуется:
раскрыть статическую неопределимость;
построить эпюру крутящих моментов;
построить эпюру касательных напряжений при d=60 мм и проверить стержень на прочность;
построить эпюру углов поворота;
проверить жесткость стержня.
раскрыть статическую неопределимость;
построить эпюру крутящих моментов;
построить эпюру касательных напряжений при d=60 мм и проверить стержень на прочность;
построить эпюру углов поворота;
проверить жесткость стержня.
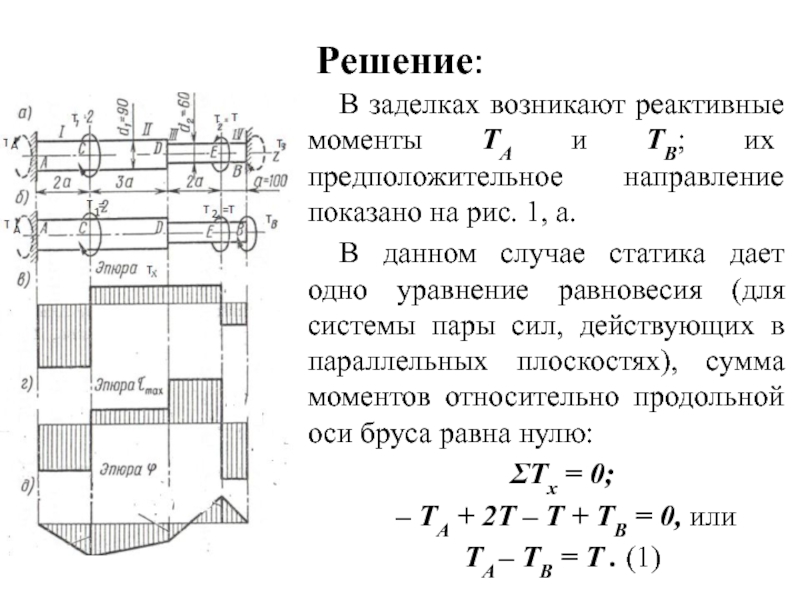
Слайд 3Решение:
В заделках возникают реактивные моменты ТА и ТВ; их предположительное направление
показано на рис. 1, а.
В данном случае статика дает одно уравнение равновесия (для системы пары сил, действующих в параллельных плоскостях), сумма моментов относительно продольной оси бруса равна нулю:
ΣТx = 0;
– ТA + 2Т – Т + ТB = 0, или
ТA – ТB = Т . (1)
В данном случае статика дает одно уравнение равновесия (для системы пары сил, действующих в параллельных плоскостях), сумма моментов относительно продольной оси бруса равна нулю:
ΣТx = 0;
– ТA + 2Т – Т + ТB = 0, или
ТA – ТB = Т . (1)
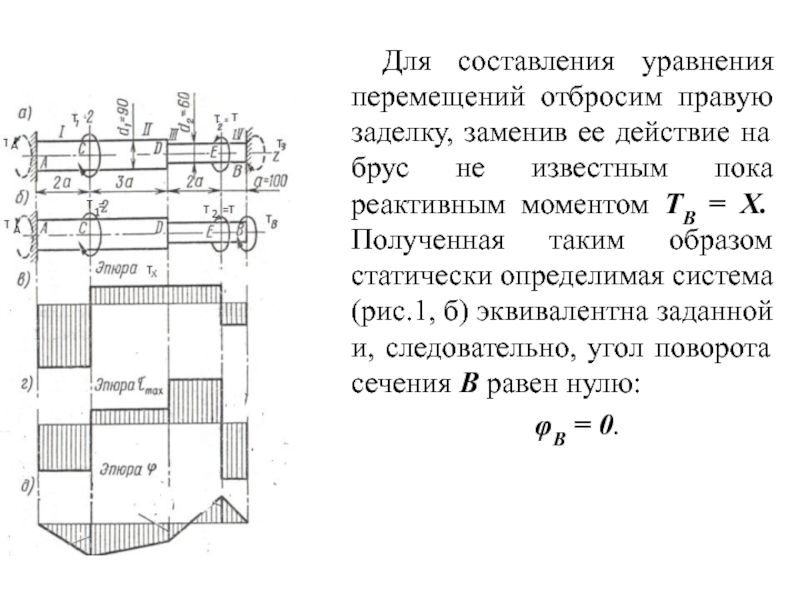
Слайд 4Для составления уравнения перемещений отбросим правую заделку, заменив ее действие на
брус не известным пока реактивным моментом ТB = Х. Полученная таким образом статически определимая система (рис.1, б) эквивалентна заданной и, следовательно, угол поворота сечения В равен нулю:
φB = 0.
φB = 0.
Слайд 5Применяя принцип независимости действия сил, запишем уравнение перемещений в виде
φB =
φBТ1 + φBТ2 + φBХ = 0. (2)
При действии только момента Т1 угол поворота сечения В равен углу закручивания участка АС, т.е.
Аналогично при действии только момента Т2
Знак минус поставлен потому, что момент Т2 направлен противоположно моменту Т1.
При действии только момента ТB = Х получим
При действии только момента Т1 угол поворота сечения В равен углу закручивания участка АС, т.е.
Аналогично при действии только момента Т2
Знак минус поставлен потому, что момент Т2 направлен противоположно моменту Т1.
При действии только момента ТB = Х получим
Слайд 6Для упрощения вычислений выразим Jp1 = πd14 / 32 через Jp2
= πd24 / 32 :
Подставляя значения угла поворота в уравнение (2) и учитывая соотношение между Jp1 и Jp2, получаем
откуда
Х = ТB = (11/20) Т.
Подставляя значение ТB в уравнение равновесия (1), найдем
ТА = (31/20) Т.
Подставляя значения угла поворота в уравнение (2) и учитывая соотношение между Jp1 и Jp2, получаем
откуда
Х = ТB = (11/20) Т.
Подставляя значение ТB в уравнение равновесия (1), найдем
ТА = (31/20) Т.
Слайд 7Эпюру крутящих моментов строим, начиная с левого конца. Проведя произвольное сечение
на участке АС и составляя для оставленной части уравнение равновесия ΣТХ = 0, получаем ТХ1 = (31/20) Т .
Согласно принятому правилу знаков, считаем момент ТХ1 отрицательным. Для остальных участков находим крутящие моменты как алгебраические суммы внешних моментов, приложенных по одну сторону (в нашем случае левую) от сечения. Отсеченные части отдельно не изображаем. Вообще следует заметить, что построение эпюры крутящих моментов совершенно аналогично построению эпюры продольных сил.
Согласно принятому правилу знаков, считаем момент ТХ1 отрицательным. Для остальных участков находим крутящие моменты как алгебраические суммы внешних моментов, приложенных по одну сторону (в нашем случае левую) от сечения. Отсеченные части отдельно не изображаем. Вообще следует заметить, что построение эпюры крутящих моментов совершенно аналогично построению эпюры продольных сил.
Слайд 8Строим эпюру касательных напряжений, пользуясь формулой
τmax = ТX / Wp
, где Wp = πD3 / 16.
Для участка АС:
Заданное значение момента умножаем на 106 для перевода из кН·м в Н·мм.
Аналогично определяем τmax в поперечных сечениях остальных участков бруса.
Ординаты эпюры τmax откладываем в ту же сторону, что и соответствующие ординаты эпюры ТX. Знак касательного напряжения при расчете на прочность никакой роли не играет, и принятое направление ординат эпюры условно.
Для участка АС:
Заданное значение момента умножаем на 106 для перевода из кН·м в Н·мм.
Аналогично определяем τmax в поперечных сечениях остальных участков бруса.
Ординаты эпюры τmax откладываем в ту же сторону, что и соответствующие ординаты эпюры ТX. Знак касательного напряжения при расчете на прочность никакой роли не играет, и принятое направление ординат эпюры условно.
Слайд 9Опасным оказалось поперечное сечение участка ВЕ. Таким образом, опасным оказалось не
то сечение. в котором крутящий момент максимален.
Проверяем условие прочности τmax ≤ [τk] .
Эпюру углов поворота строим, начиная от защемленного конца. Ординаты этой эпюры в выбранном масштабе дают величины углов поворота соответствующих поперечных сечений бруса. Эпюра строится совершенно аналогично эпюре линейных перемещений.
Проверяем условие прочности τmax ≤ [τk] .
Эпюру углов поворота строим, начиная от защемленного конца. Ординаты этой эпюры в выбранном масштабе дают величины углов поворота соответствующих поперечных сечений бруса. Эпюра строится совершенно аналогично эпюре линейных перемещений.
Слайд 10В пределах каждого из участков бруса эпюра линейна, поэтому достаточно вычислить
углы поворота только для граничных сечений участков: угол поворота сечения С, равный углу закручивания участка АС (со знаком -):
где принято для стали G = 8 ∙104 Н/мм2 ;
угол поворота, например, сечения Е относительно А, равный углу закручивания участка АЕ:
где принято для стали G = 8 ∙104 Н/мм2 ;
угол поворота, например, сечения Е относительно А, равный углу закручивания участка АЕ:
Слайд 11
Аналогично вычисляются углы поворота остальных граничных сечений.
φmax = T∙ℓ / G∙Jp
≤ [φ]
Проверяем жесткость стержня по формуле:








![Аналогично вычисляются углы поворота остальных граничных сечений.φmax = T∙ℓ / G∙Jp ≤ [φ]Проверяем жесткость стержня](/img/tmb/5/471753/b2b254ea906ceca82a318c097a4415dc-800x.jpg)





