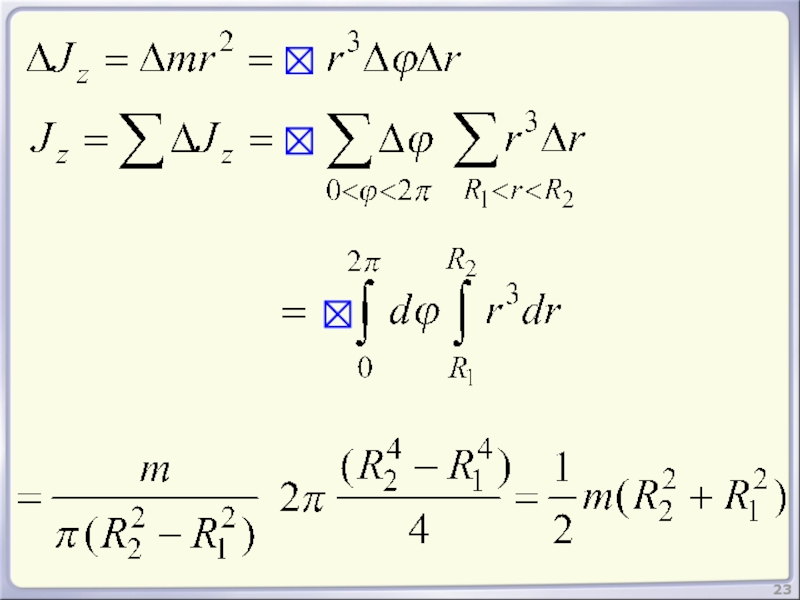- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механика твердого тела. (Лекция 4) презентация
Содержание
- 1. Механика твердого тела. (Лекция 4)
- 2. 02 Физическим телом
- 3. §§ Плоское движение 03 Поступательным называется движение,
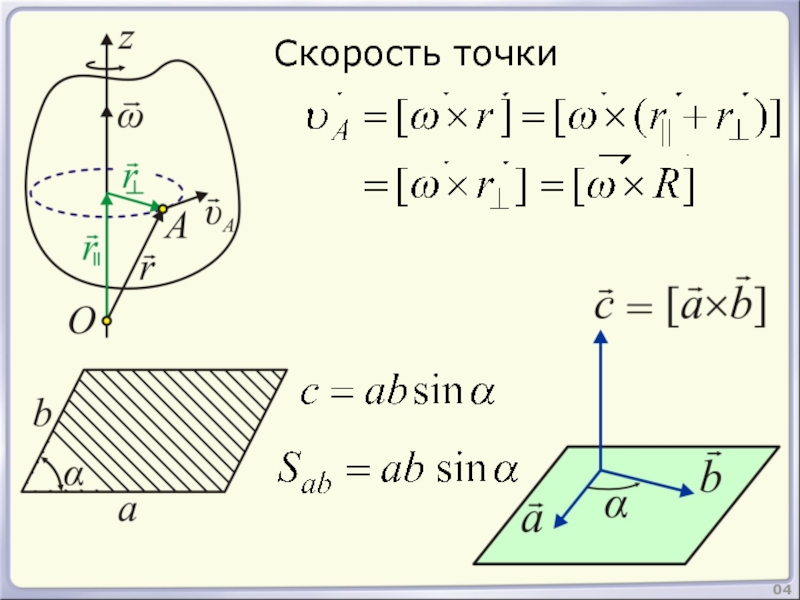
- 4. 04 Скорость точки
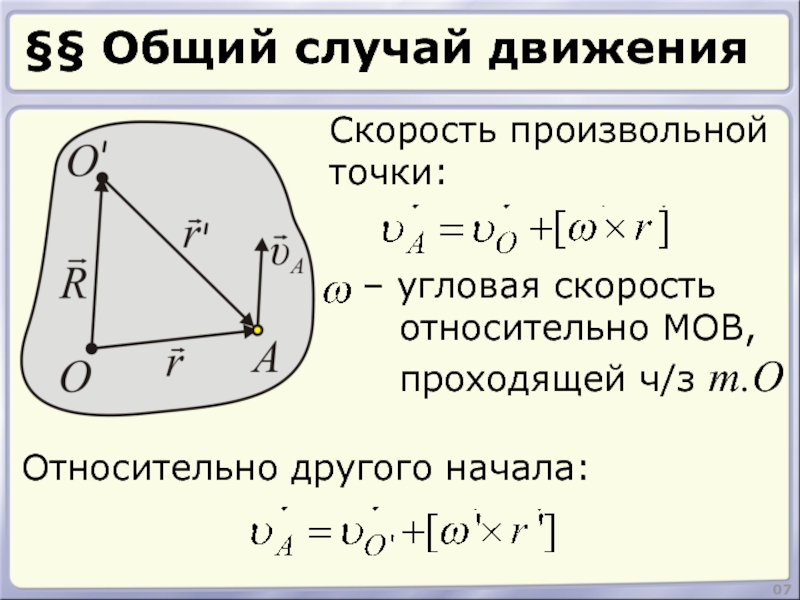
- 7. §§ Общий случай движения 07 Скорость произвольной точки: Относительно другого начала:
- 8. – не зависит от выбора т.О. 08 следовательно:
- 9. §§ Момент силы 09 Моментом силы относительно
- 10. Свойства: 10 1) при переносе силы
- 11. 11
- 12. §§ Момент относительно оси 12 Будем раскладывать
- 13. 13 – момент силы относительно
- 14. §§ Момент импульса 14 Моментом импульса м.т.
- 15. 15 – уравнение моментов производная по времени
- 16. 16 суммируя уравнения, получаем: производная по времени
- 17. Закон сохранения момента импульса 17 если момент
- 18. §§ Работа и кин. энергия 18 При повороте тела совершается работа:
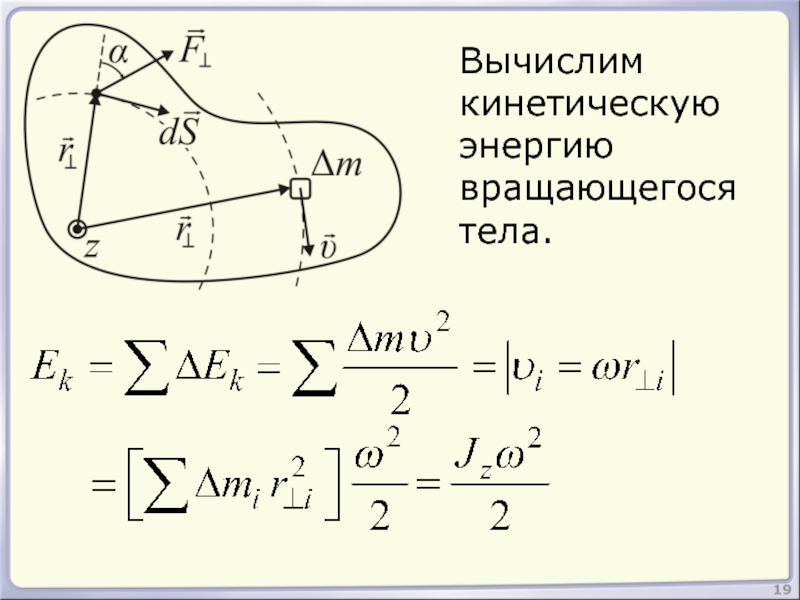
- 19. 19 Вычислим кинетическую энергию вращающегося тела.
- 20. 20 – момент инерции м.т. массой
- 21. §§ Уравнение динамики 21 Пусть м.т. двигается
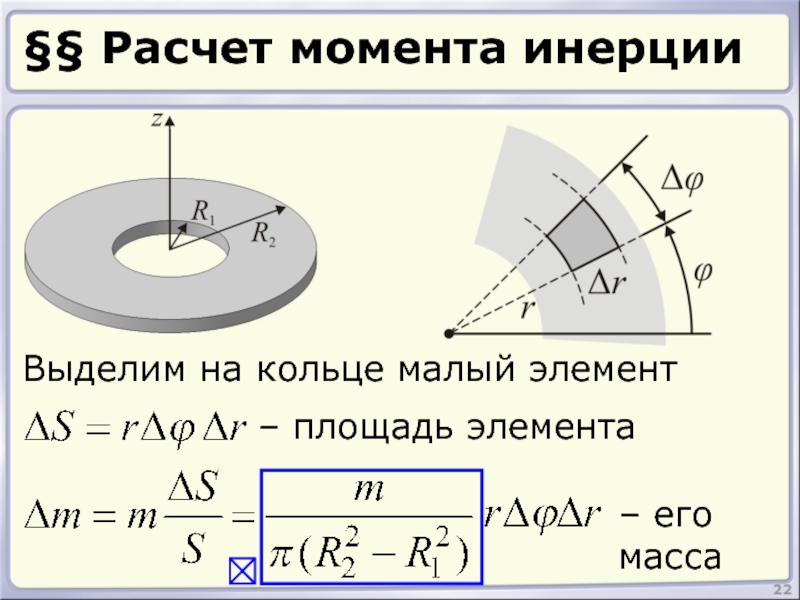
- 22. §§ Расчет момента инерции 22 Выделим на
- 23. 23
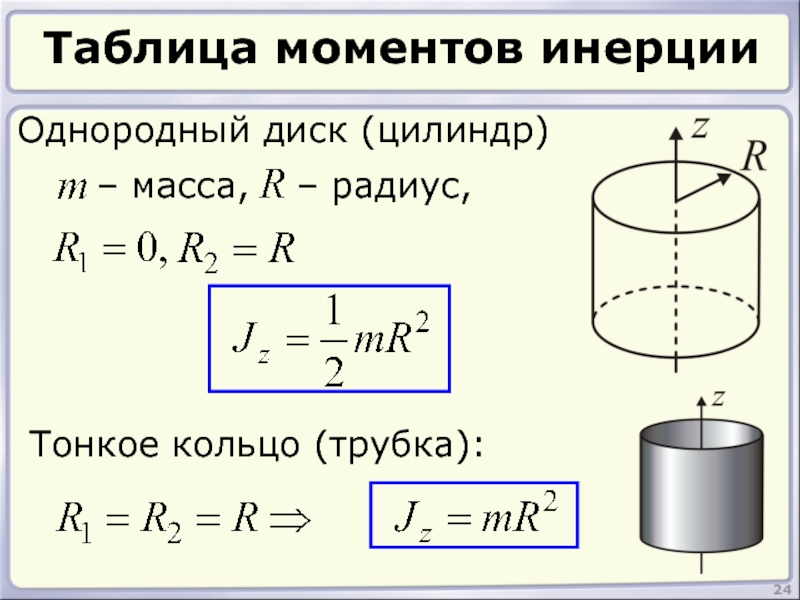
- 24. Таблица моментов инерции 24 Однородный диск (цилиндр) Тонкое кольцо (трубка):
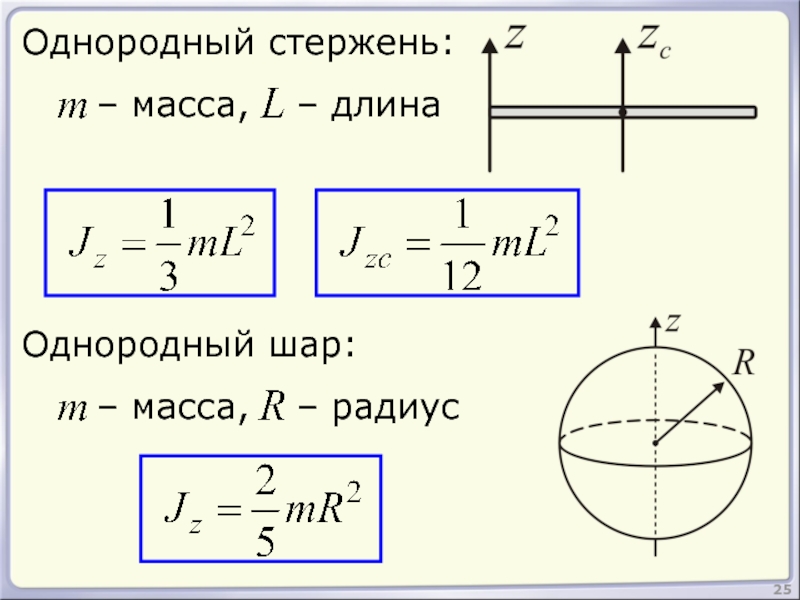
- 25. 25 Однородный стержень: Однородный шар:
- 26. 26 Замечания: 1) момент инерции для тел
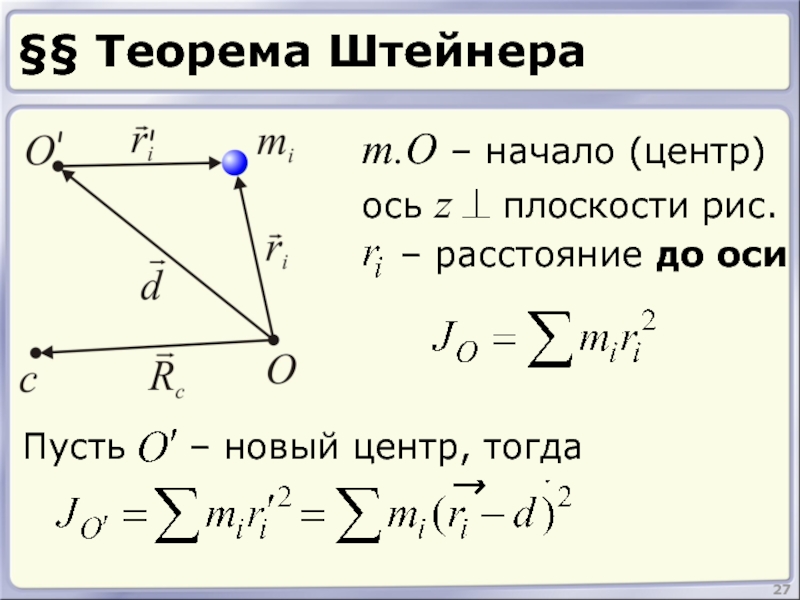
- 27. §§ Теорема Штейнера 27 т.О – начало (центр)
- 28. 28
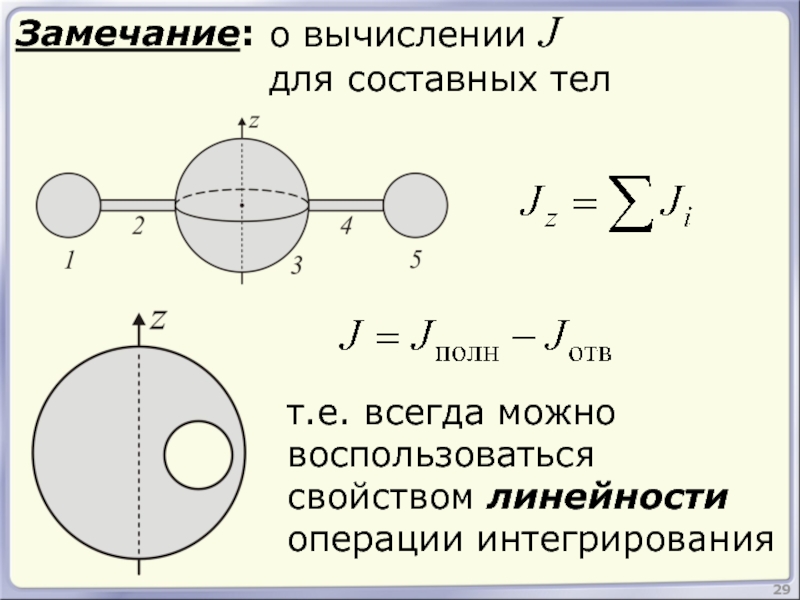
- 29. Замечание: 29 о вычислении J для
Слайд 202
Физическим телом
система взаимодействующих частиц
массой Δmi и объемом ΔVi, непрерывно
заполняющих объем V.
Абсолютно твердое тело (АТТ)
это система м.т. (частиц), расстояние
между которыми постоянно.
т.е. это тело, деформациями которого,
в условиях данной задачи, можно
пренебречь.
Слайд 3§§ Плоское движение
03
Поступательным называется движение,
при котором любая из прямых,
связанных с двигающимся
остается параллельной ее начальному
направлению.
Вращательным называется движение,
при котором все точки тела двигаются
по окружностям,
центры которых лежат
на одной прямой,
называемой осью
вращения.
Слайд 5
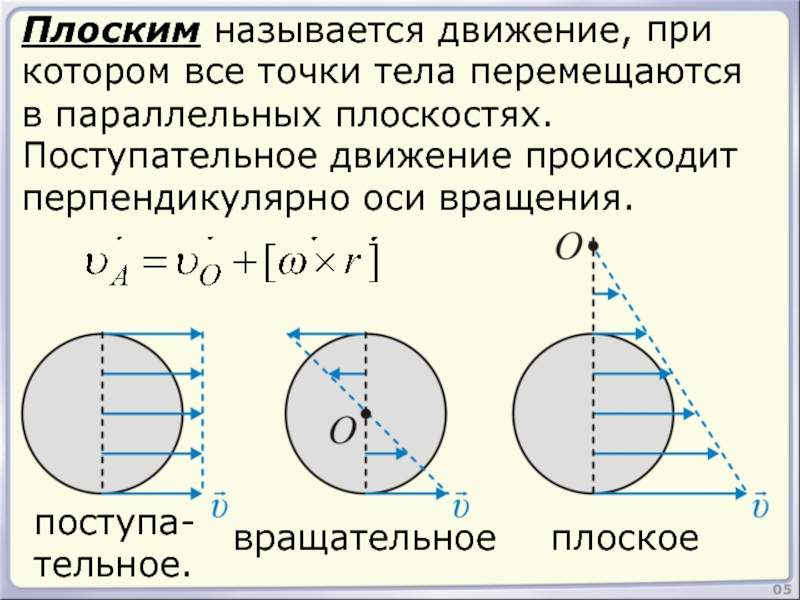
котором все точки тела перемещаются
в параллельных плоскостях.
05
Плоским называется движение,
Поступательное движение происходит
перпендикулярно оси вращения.
поступа-
тельное.
вращательное
плоское
Слайд 6
переведено из одного положения
в другое
06
При плоском движении
путем поворота относительно
мгновенной оси.
С течением времени мгновенная ось
непрерывно перемещается как в теле,
так и в пространстве.
Пример: качение цилиндра
Слайд 9§§ Момент силы
09
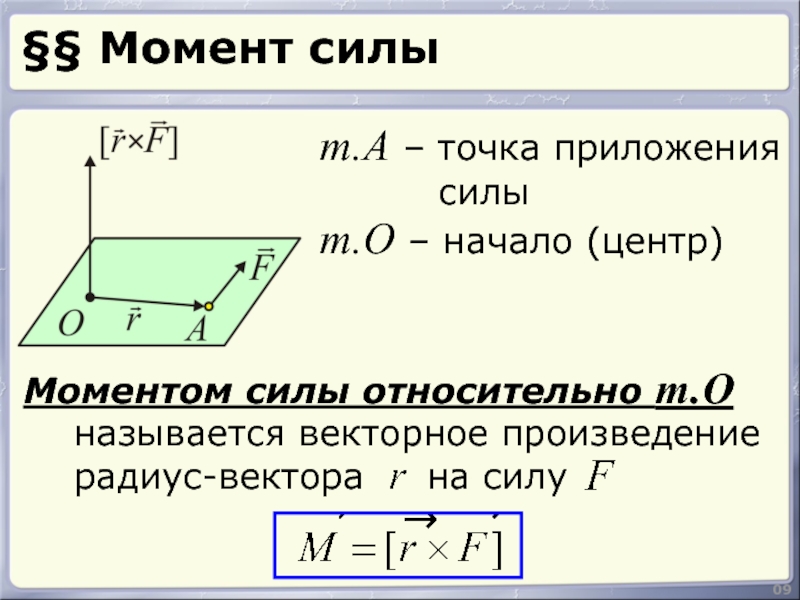
Моментом силы относительно т.О
т.О – начало (центр)
т.A – точка
силы
Слайд 10Свойства:
10
1) при переносе силы
вдоль линии ее
действия
силы не изменяется
т.е. момент равнодействующей силы
равен сумме моментов сил.
Слайд 1111
линии действия силы)
две равные и противоположно
направленные силы
, линии
действия которых смещены
одна относительно другой,
называются парой сил.
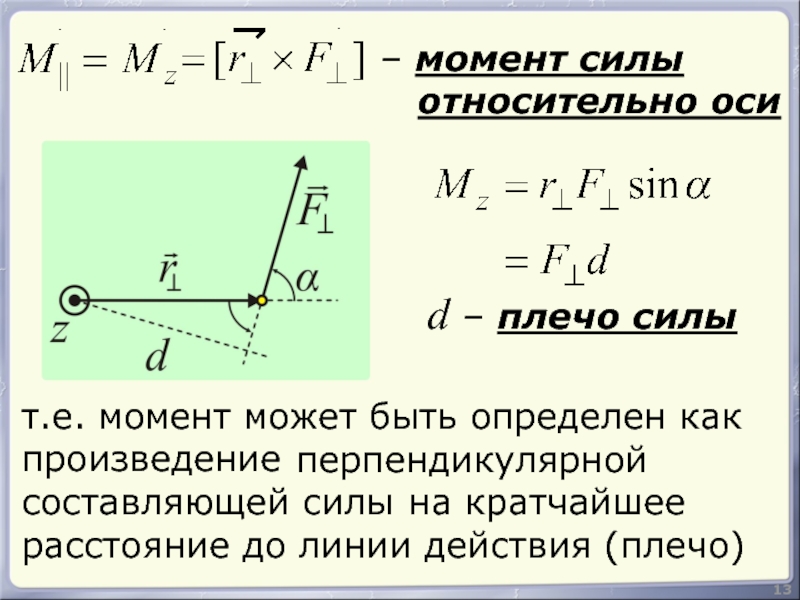
Слайд 1313
– момент силы
относительно оси
d – плечо силы
т.е. момент может
произведение
перпендикулярной
составляющей силы
на кратчайшее
расстояние до линии действия (плечо)
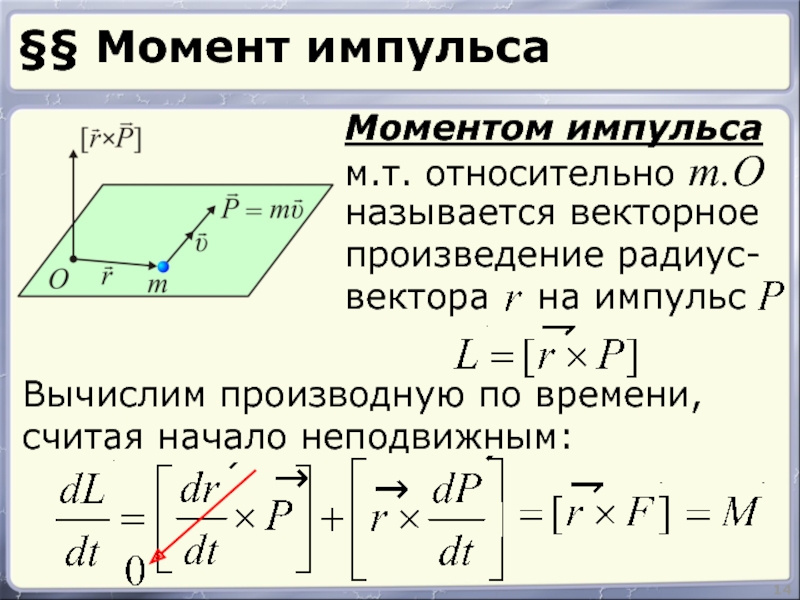
Слайд 14§§ Момент импульса
14
Моментом импульса
м.т. относительно т.О
Вычислим производную по времени,
считая начало неподвижным:
Слайд 1515
– уравнение моментов
производная по времени м.и. м.т.
относительно неподвижного начала
равна моменту действующей
относительно того же начала
Рассмотрим систему из N частиц
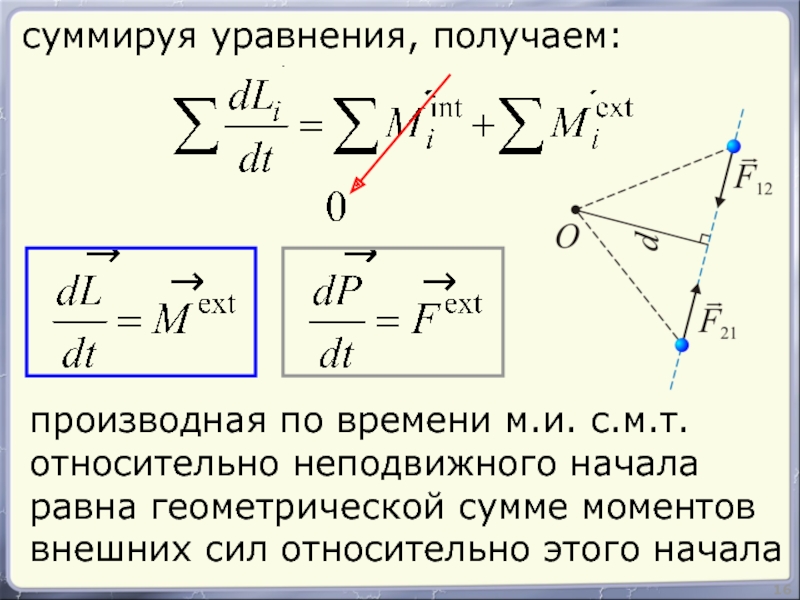
Слайд 1616
суммируя уравнения, получаем:
производная по времени м.и. с.м.т.
относительно неподвижного начала
равна геометрической сумме
внешних сил относительно этого начала
Слайд 17Закон сохранения момента импульса
17
если момент внешних сил относительно неподвижного начала равен
то м.и. системы относительно того же
начала остается постоянным во времени
в проекции на ось:
если момент внешних сил относительно оси равен нулю,
то м.и. системы
относительно той же оси остается
постоянным.
Слайд 20
20
– момент инерции м.т. массой m
– момент инерции с.м.т.
Величина Jz –
тела (точки) при вращении.
– для вращательного
движения
– для плоского
движения
Слайд 21§§ Уравнение динамики
21
Пусть м.т. двигается по окружности:
подставим в уравнение моментов
– это
вращательного движения (ОУДВД)
для неизменной
с.м.т. (атт)
Слайд 2626
Замечания:
1) момент инерции для тел простой
формы:
2) в справочниках
инерции относительно осей,
проходящих через центр масс
Слайд 29Замечание:
29
о вычислении J
для составных тел
т.е. всегда можно
воспользоваться
свойством линейности
операции интегрирования
