- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сопротивление материалов. Курс лекций презентация
Содержание
- 1. Сопротивление материалов. Курс лекций
- 2. ЛИТЕРАТУРА Степин П.А. Сопротивление материалов. - М.:
- 3. Исходные понятия и определения Сопротивление
- 4. Основные понятия статики Статика – раздел механики,
- 5. Основные понятия статики Сила есть мера механического
- 6. Основные понятия статики Линия действия силы
- 7. Основные понятия статики Система сил – совокупность
- 8. Аксиомы статики 1. Под действием взаимно уравновешивающихся
- 9. Аксиомы статики 3. Действие системы сил на
- 10. Аксиомы статики 4. Равнодействующая двух пересекающихся сил
- 11. Основные понятия статики Главный вектор системы сил
- 12. Основные понятия статики Момент силы
- 13. Основные понятия статики О r F Z
- 14. Основные понятия статики Главный момент Мо системы
- 15. Схематизация элементов конструкций центр
- 16. Виды внешних нагрузок Сосредоточенная сила F –
- 17. Виды нагрузок
- 18. Виды нагрузок Статические – не изменяющиеся или
- 19. Опорные реакции Твердое тело называют свободным, если
- 20. Опорные реакции Принцип освобождаемости твердых тел от
- 21. Классификация опор и опорные реакции неподвижная
- 22. Определение опорных реакций Уравнения равновесия
- 23. Определение опорных реакций а Приравняем к
- 24. Определение опорных реакций ∑Z = 0 ∑МА
- 25. Определение опорных реакций YA YB ℓ =
- 26. Определение опорных реакций ∑Z = 0 ∑MA
- 27. Виды деформаций Деформации (изменения размеров и формы
- 28. Виды деформаций S S
- 29. Основные допущения о свойствах материалов материал
- 30. Гипотезы о характере деформаций гипотеза плоских сечений
- 31. Гипотезы о характере деформаций и другие принципы
- 32. Принцип Сен - Венана В точках тела
- 33. Внутренние силовые факторы (наиболее общий случай) изгибающий момент
- 34. Внутренние силовые факторы (частные случаи) Если в
- 35. Метод сечений (для определения внутренних силовых факторов)
- 36. Метод сечений (для определения ВСФ) 3. Составляют
- 37. Напряжение – внутренняя сила, приходящаяся на единицу
- 38. Напряжения Среднее напряжение, приходящееся на единицу площади
- 39. Напряженное состояние в данной точке это совокупность
- 40. Напряженное состояние в данной точке σ –
- 41. Главные площадки и главные напряжения Главными площадками
- 42. Виды напряженного состояния Объемное напряженное состояние: σ1≠0
- 43. Центральное растяжение и сжатие Центральным растяжением (сжатием)
- 44. Центральное растяжение и сжатие гипотеза плоских сечений
- 45. Центральное растяжение и сжатие Z Y
- 46. Построение эпюры Nz при центральном растяжении (сжатии)
- 47. Проверка правильности построения эпюр Nz Если в
- 48. Деформации при растяжении и сжатии - относительная
- 49. Закон Гука. Коэффициент Пуассона. - напряжение
- 50. Абсолютное удлинение стержня под действием произвольной системы
- 51. Испытание на растяжение Разрушение образца
- 52. Диаграмма растяжения с площадкой текучести
- 53. Диаграмма растяжения без площадки текучести σ0,2 –
- 54. Испытание на сжатие d0 h0
- 55. Диаграммы растяжения и сжатия пластичного и хрупкого
- 56. Расчеты на прочность при растяжении и сжатии
- 57. Допускаемые напряжения и коэффициент запаса прочности -
- 58. Геометрические характеристики плоских сечений Площадь
- 59. Геометрические характеристики плоских сечений В расчетах
- 60. Геометрические характеристики плоских сечений Геометрические
- 61. Статический момент сечения Статический момент инерции
- 62. Зависимость статического момента одного и
- 63. Осевой момент инерции Осевой момент инерции
- 64. Полярный момент инерции Полярный момент
- 65. Центробежный момент инерции Центробежный
- 66. Главные оси сечения Для
- 67. Главные оси сечения Относительно главных
- 68. Определение моментов инерции простых фигур
- 69. Зависимость между моментами инерции относительно параллельных осей
- 70. Определение моментов инерции простых фигур Треугольник
- 71. Определение моментов инерции простых фигур Круг y
- 72. A A A A 4 А A A A 4 3 A 4
- 73. h b 4 b d 4
- 74. ИЗГИБ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ГИПОТЕЗЫ. Изгиб –
- 75. ИЗГИБ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ГИПОТЕЗЫ. Чистый изгиб
- 76. ИЗГИБ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ГИПОТЕЗЫ
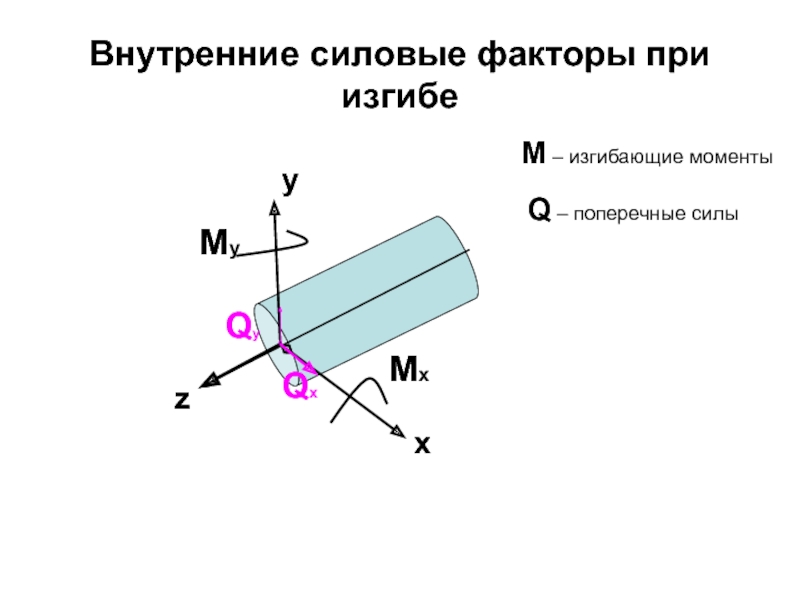
- 77. Внутренние силовые факторы при изгибе
- 78. Определение внутренних силовых факторов при изгибе
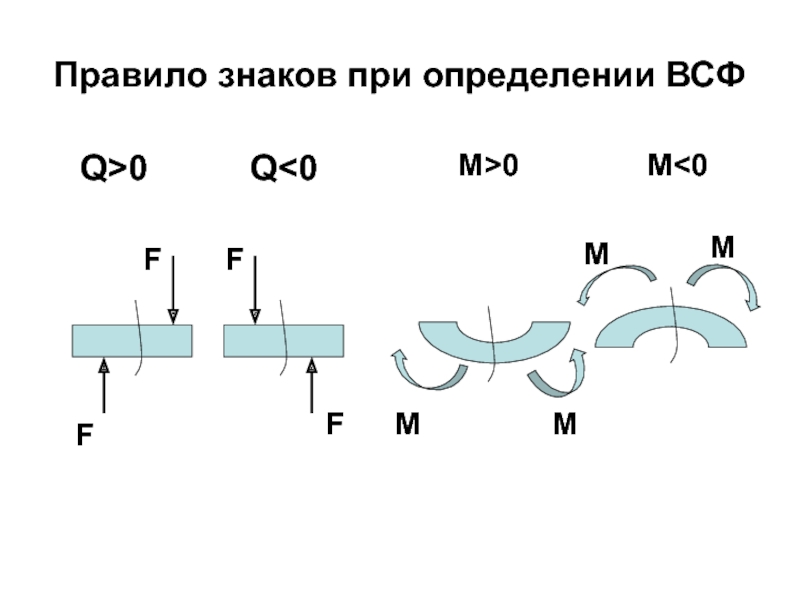
- 79. Правило знаков при определении ВСФ F F F F Q>0 Q0 M
- 80. Дифференциальные зависимости при изгибе YA
- 81. Дифференциальные зависимости при изгибе YA
- 82. Дифференциальные зависимости при изгибе Вторая производная от изгибающего момента равна интенсивности распределенной нагрузки.
- 83. Построение эпюр М и Q YA 3м
- 84. Построение эпюры Nz при центральном растяжении (сжатии)
- 85. Проверка правильности построения эпюр Q и М
- 86. Участку балки с распределенной нагрузкой q соответствует
- 87. Определение нормальных напряжений при изгибе Допущения: гипотеза
- 88. Закон распределения внутренних сил при плоском чистом
- 89. Закон распределения внутренних сил при плоском чистом
- 90. Определение значений нормальных напряжений из уравнений равновесия
- 91. Определение значений нормальных напряжений из уравнений равновесия
- 92. Определение значений нормальных напряжений из уравнений равновесия
- 93. Определение значений нормальных напряжений из уравнений равновесия
- 94. Определение значений нормальных напряжений из уравнений равновесия
- 95. Расчеты на прочность при изгибе проверочный
- 96. Касательные напряжения при изгибе Формула Журавского (для
- 97. Распределение по сечению касательных напряжений Прямоугольное сечение
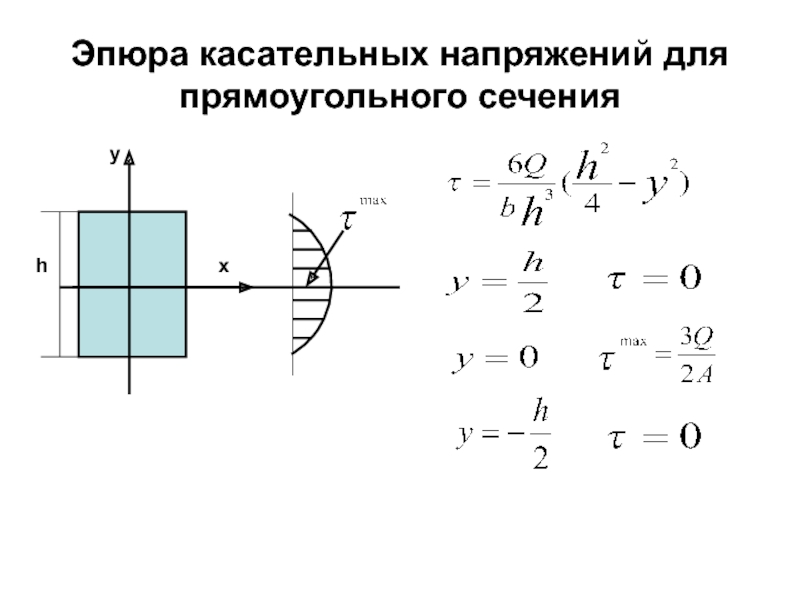
- 98. Эпюра касательных напряжений для прямоугольного сечения
- 99. Определение перемещений в балках постоянного сечения методом
- 100. Определение перемещений в балках постоянного сечения методом
- 101. Определение перемещений в балках постоянного сечения методом
- 102. Определение перемещений в балках постоянного сечения методом
- 103. Определение перемещений в балках постоянного сечения методом
- 104. Дифференциальное уравнение упругой линии балки при изгибе
- 105. Дифференциальное уравнение упругой линии балки при изгибе
- 106. Дифференциальное уравнение упругой линии балки при изгибе
- 108. Универсальное уравнение. Уравнение прогибов Уравнение углов поворота
- 109. Задача 6.4. ,
- 110. Кручение Кручение – вид деформации, при котором
- 111. Кручение Кручение прямого бруса происходит при нагружении
- 112. Кручение Крутящие моменты, возникающие в поперечных сечениях
- 113. Кручение Изменение крутящих моментов по длине бруса
- 114. Кручение Обозначения: . · + · + + · + ·
- 115. Кручение Принятое правило знаков необходимо выдержать на всем протяжении эпюры.
- 116. Кручение М3 М1 = 7кН·м;
- 117. Кручение + + Mz,
- 118. Расчет на прочность при кручении В поперечном
- 119. Подбор круглого сечения стержня по полярному моменту
- 120. Теории прочности Теории прочности – гипотезы об
- 121. Составление условия прочности для линейного напряженного состояния
- 122. Условие прочности для сложного напряженного состояния
- 123. Эквивалентное напряжение - напряжение, при котором
- 124. Первая теория прочности (теория наибольших нормальных напряжений)
- 125. Вторая теория прочности (теория относительных удлинений) Опасное
- 126. Третья теория прочности (теория наибольших касательных напряжений)
- 127. Третья теория прочности (теория наибольших касательных напряжений)
- 128. Третья теория прочности (теория наибольших касательных напряжений)
- 129. Четвертая теория прочности (энергетическая) Прочность материала при
- 130. Четвертая теория прочности (энергетическая) Теория подтверждается
- 131. Сложное сопротивление Сложное сопротивление – совместное действие
- 133. Определение суммарного изгибающего момента: Определение эквивалентного
- 134. РАСЧЕТЫ НА УСТАЛОСТЬ
- 135. Раздел 4. Сдвиг и кручение Чистый
- 137. Напряжения и деформации при кручении Wp
- 138. Раздел 6. Напряженное и деформированное состояние
- 139. Линейное напряженное состояние На наклонной площадке pα
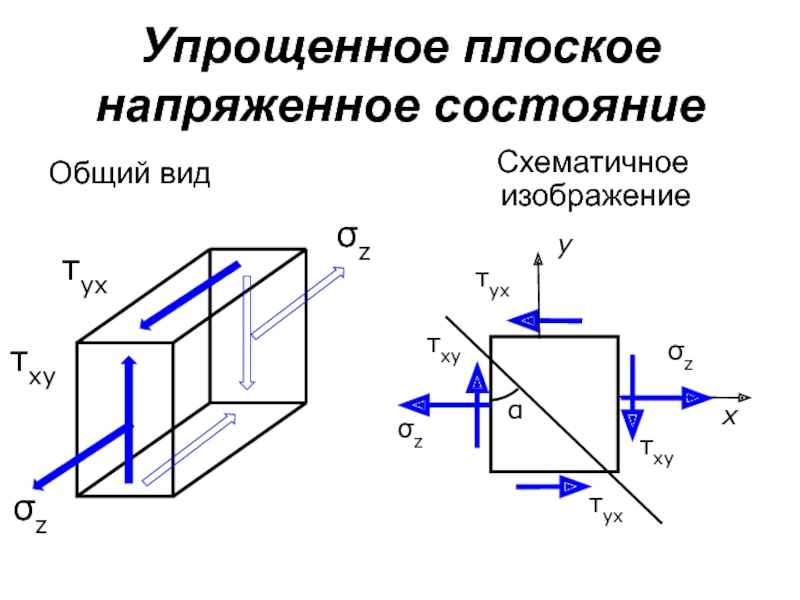
- 140. Упрощенное плоское напряженное состояние Схематичное изображение Общий вид
- 141. Напряжения на наклонной площадке Главные напряжения Максимальные касательные напряжения
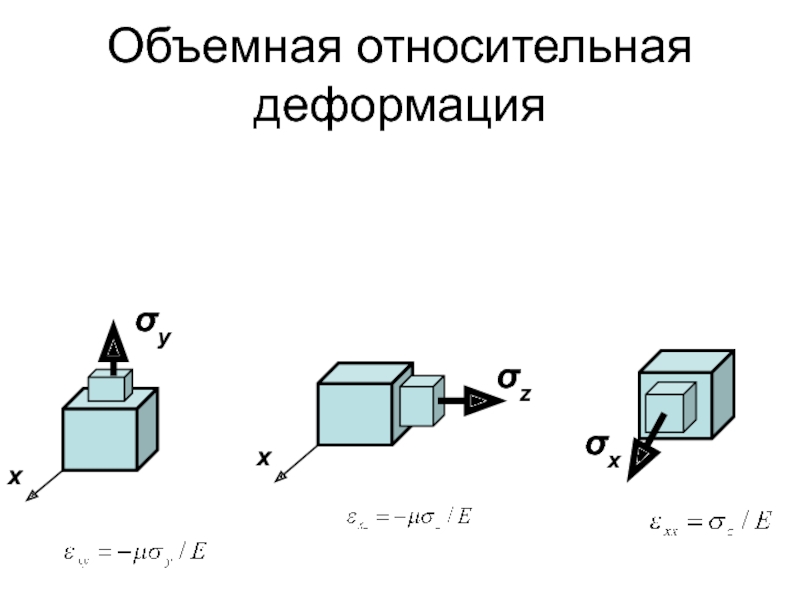
- 142. Обобщенный закон Гука Объемная относительная деформация
- 143. Критерии предельного состояния материала σ2
- 144. Критерии хрупкого разрушения наибольших нормальных напряжений
- 145. Критерии появления пластических деформаций наибольших касательных
- 146. Теория Мора - опытные точки
- 147. Объемная относительная деформация
- 148. Геометрические характеристики плоских сечений Площадь Статические моменты Координаты центра тяжести
- 149. Моменты инерции Осевые Центробежный Полярный
- 150. Преобразование моментов при параллельном переносе осей
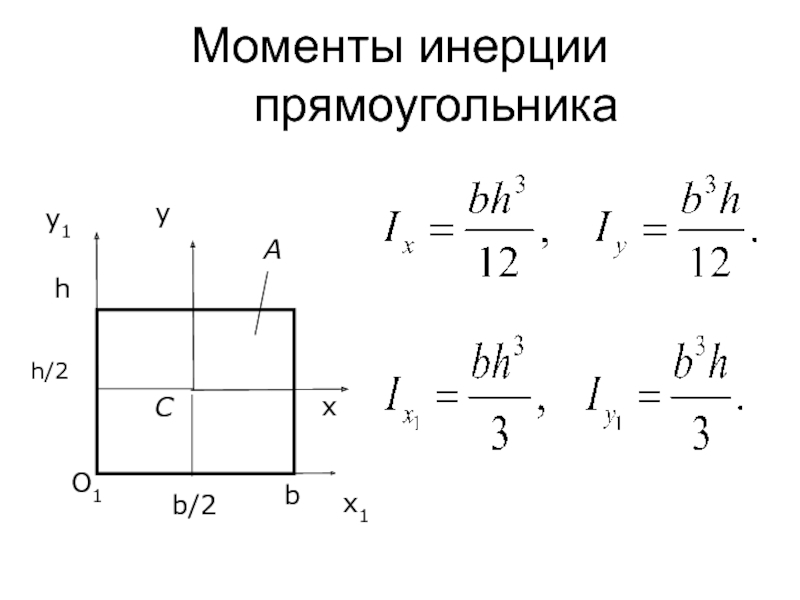
- 151. Моменты инерции прямоугольника x1 y1
- 152. Моменты инерции y A x d D Круга Кольца
- 153. Изгиб прямых стержней - момент сопротивления
Слайд 2ЛИТЕРАТУРА
Степин П.А. Сопротивление материалов. - М.: Высшая школа, 2000.
Феодосьев В.И. Сопротивление
№ 880. Шинкин В.Н. Сопротивление материалов. Курс лекций. 2005.
№ 1840. Архангельский А.В., Белов М.И. Прикладная механика. Учебно-методическое пособие. 2003.
Слайд 3Исходные понятия и определения
Сопротивление материалов – наука о расчете
Прочность – свойство материала, не разрушаясь, воспринимать внешние воздействия (нагрузки, температуры и др.).
Жесткость - способность тела или конструкции сопротивляться образованию деформаций.
Устойчивость - способность конструкций сопротивляться усилиям, стремящихся вывести их из состояния равновесия.
Слайд 4Основные понятия статики
Статика – раздел механики, в котором изучаются методы преобразования
Абсолютно твердое тело – тело, расстояния между любыми точками которого остаются неизменными. Условия равновесия сил, приложенных к абсолютно твердому телу, используют при изучении действия сил на деформируемое тело с соответствующими дополнениями
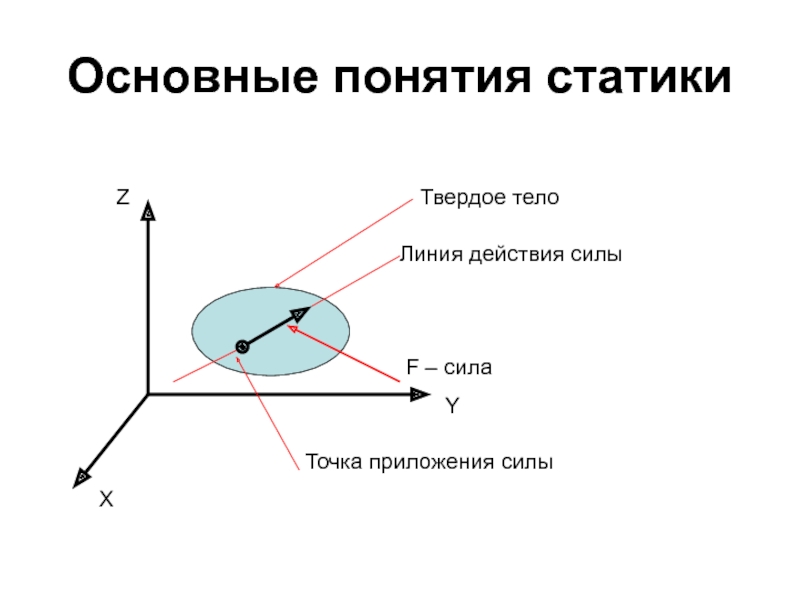
Слайд 5Основные понятия статики
Сила есть мера механического взаимодействия твердых тел, в результате
Сила – векторная величина, характеризуемая модулем, точкой приложения и направлением.
Слайд 7Основные понятия статики
Система сил – совокупность нескольких сил, действующих на данное
Сила, эквивалентная некоторой системе сил – равнодействующая сила.
Внешние силы – действуют на материальные точки (тела) данной системы со стороны материальных точек (тел) не принадлежащих этой системе.
Внутренние силы – силы взаимодействия между телами данной системы.
Слайд 8Аксиомы статики
1. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится
2. Две силы, приложенные к твердому телу взаимно уравновешиваются только в том случае, если их модули равны и они направлены по одной прямой в противоположные стороны (уравновешивающие силы).
Слайд 9Аксиомы статики
3. Действие системы сил на твердое тело не изменится, если
Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменным ее модуль и направление.
Слайд 10Аксиомы статики
4. Равнодействующая двух пересекающихся сил приложена в точке их пересечения
5. Всякому действию соответствует равное и противоположно направленное противодействие (закон Ньютона).
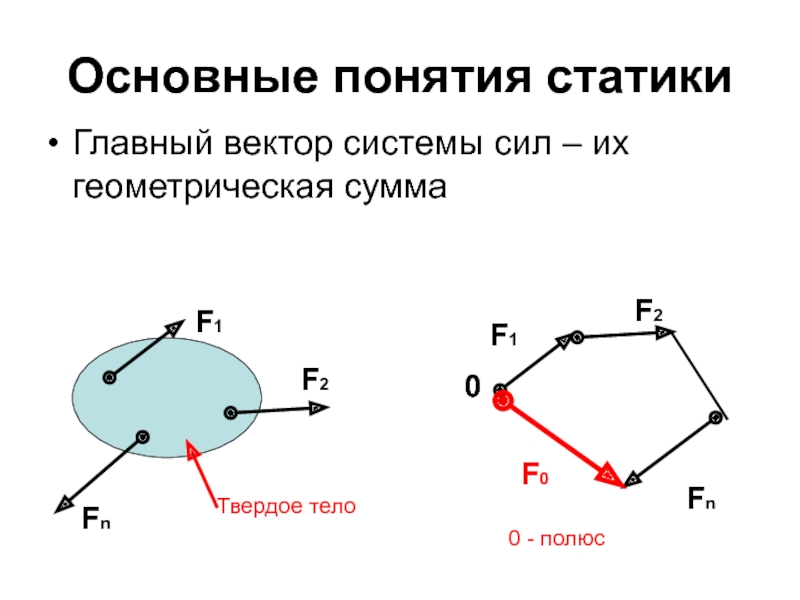
Слайд 11Основные понятия статики
Главный вектор системы сил – их геометрическая сумма
F1
F2
Fn
F1
F2
Fn
F0
0
0 -
Твердое тело
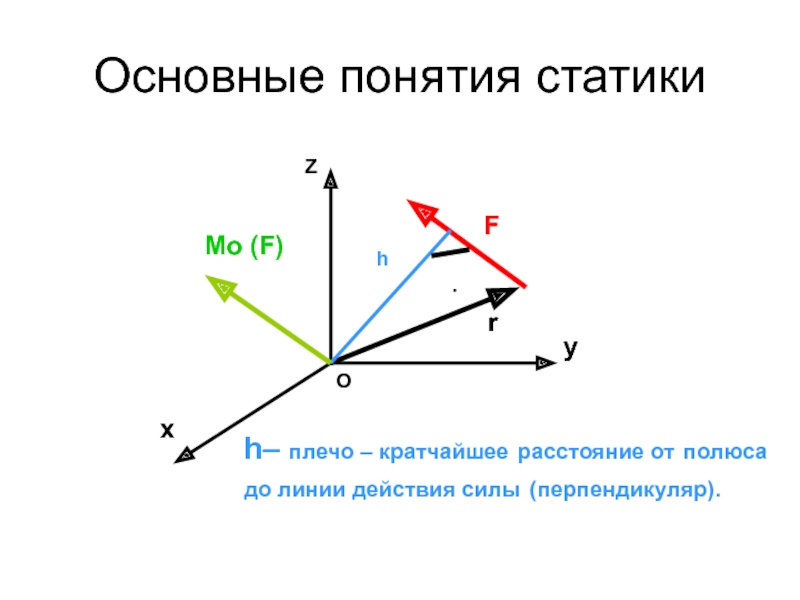
Слайд 12Основные понятия статики
Момент силы относительно точки – векторное произведение
Слайд 13Основные понятия статики
О
r
F
Z
x
y
Mo (F)
h
∙
h– плечо – кратчайшее расстояние от полюса до
Слайд 14Основные понятия статики
Главный момент Мо системы сил относительно выбранной точки –
Необходимое и достаточное условие равновесия системы сил:
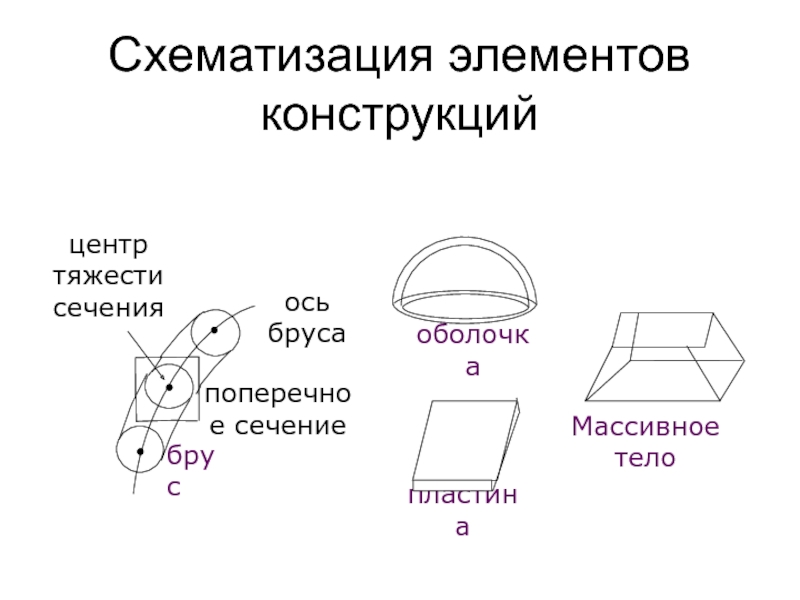
Слайд 15Схематизация элементов конструкций
центр
тяжести
сечения
брус
поперечное сечение
ось бруса
пластина
Массивное тело
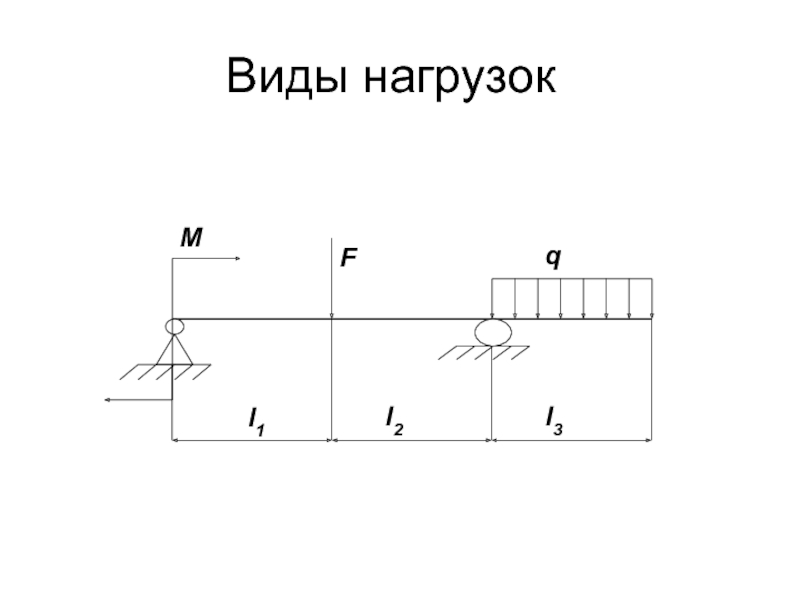
Слайд 16Виды внешних нагрузок
Сосредоточенная сила F – сила, которую можно считать приложенной
Распределенная сила действует вдоль линии (линейная нагрузка q, Н/м), на некоторой площадке (поверхностное давление p, Н/м2) или в некотором объеме (объемные силы γ, Н/м³).
Сосредоточенный момент М – момент, который можно считать приложенным в точке; размерность – Н·м.
Распределенный момент m действует вдоль линии, Н·м/м.
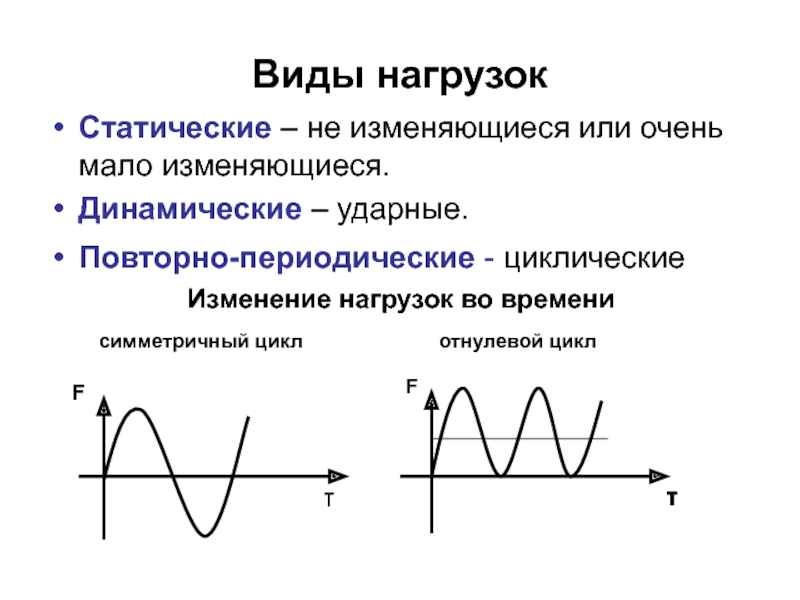
Слайд 18Виды нагрузок
Статические – не изменяющиеся или очень мало изменяющиеся.
Динамические – ударные.
Повторно-периодические
Изменение нагрузок во времени
F
τ
F
τ
симметричный цикл
отнулевой цикл
Слайд 19Опорные реакции
Твердое тело называют свободным, если оно может перемещаться в пространстве
Связь – тело ограничивающее движение данного твердого тела.
Силы, действующие на несвободное твердое тело:
Внешние и внутренние;
Задаваемые (активные);
Реакции связей (силы, выражающие механическое действие связей на тело) .
Слайд 20Опорные реакции
Принцип освобождаемости твердых тел от связей:
Несвободное твердое тело можно рассматривать
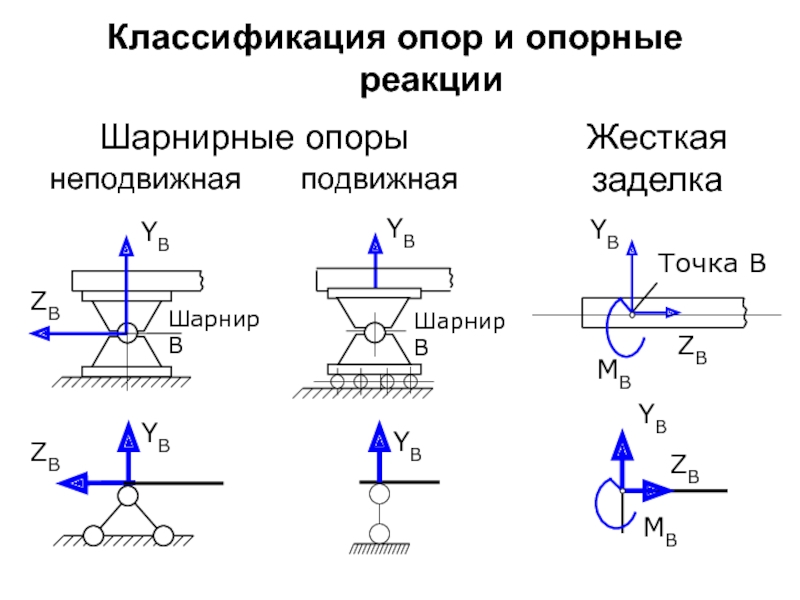
Слайд 21Классификация опор и опорные реакции
неподвижная
Точка В
YB
ZB
MB
подвижная
Шарнирные опоры
Жесткая заделка
Слайд 22Определение опорных реакций
Уравнения равновесия для определения опорных реакций можно
∑Z = 0; ∑Y = 0; ∑M = 0.
∑Z= 0; ∑Ma = 0; ∑Mb = 0.
∑Ma = 0; ∑Mb;= 0; ∑Mc = 0
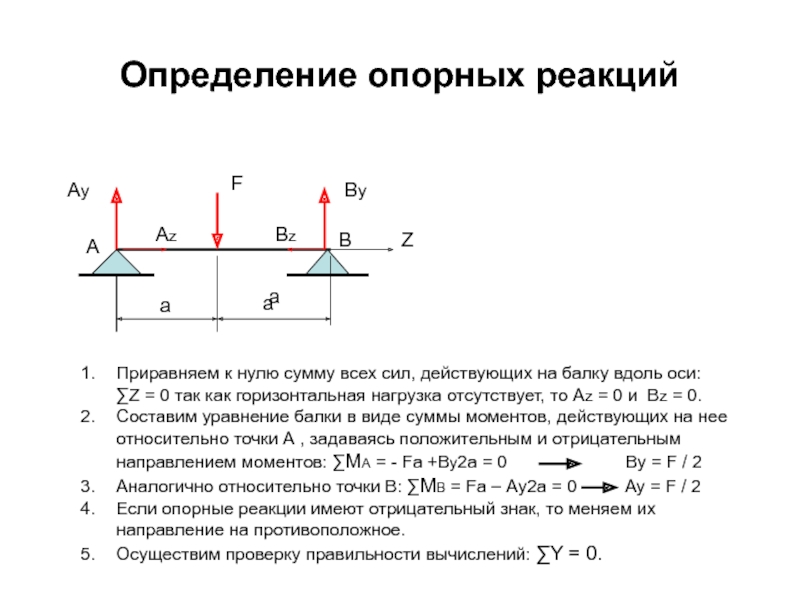
Слайд 23Определение опорных реакций
а
Приравняем к нулю сумму всех сил, действующих на балку
Составим уравнение балки в виде суммы моментов, действующих на нее относительно точки А , задаваясь положительным и отрицательным направлением моментов: ∑МА = - Fa +By2a = 0 By = F / 2
Аналогично относительно точки В: ∑МВ = Fа – Аy2a = 0 Ay = F / 2
Если опорные реакции имеют отрицательный знак, то меняем их направление на противоположное.
Осуществим проверку правильности вычислений: ∑Y = 0.
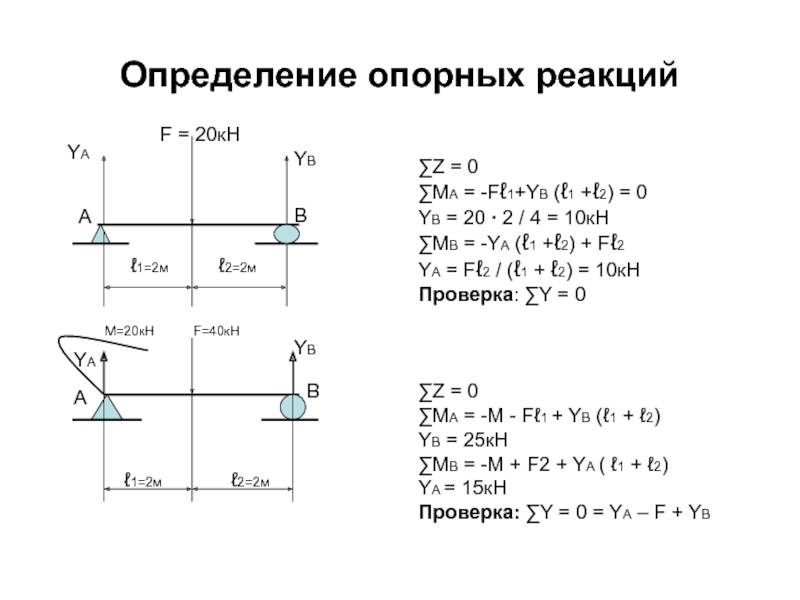
Слайд 24Определение опорных реакций
∑Z = 0
∑МА = -Fℓ1+YB (ℓ1 +ℓ2) = 0
YB
∑МВ = -YA (ℓ1 +ℓ2) + Fℓ2
YA = Fℓ2 / (ℓ1 + ℓ2) = 10кН
Проверка: ∑Y = 0
∑Z = 0
∑МА = -М - Fℓ1 + YB (ℓ1 + ℓ2)
YB = 25кН
∑МВ = -M + F2 + YА ( ℓ1 + ℓ2)
YА = 15кН
Проверка: ∑Y = 0 = YA – F + YB
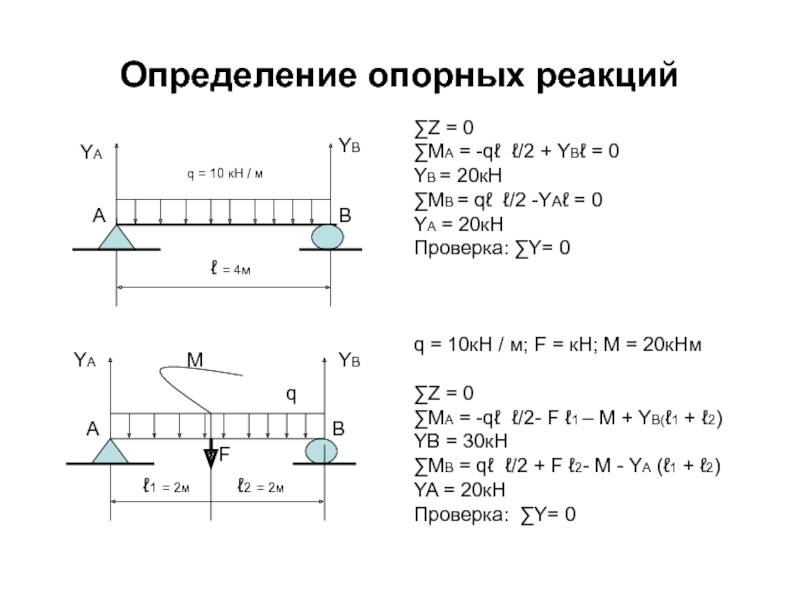
Слайд 25Определение опорных реакций
YA
YB
ℓ = 4м
q = 10 кН / м
A
B
∑Z =
∑MA = -qℓ ℓ/2 + YBℓ = 0
YB = 20кН
∑MВ = qℓ ℓ/2 -YAℓ = 0
YA = 20кН
Проверка: ∑Y= 0
q = 10кН / м; F = кН; М = 20кНм
∑Z = 0
∑MA = -qℓ ℓ/2- F ℓ1 – M + YB(ℓ1 + ℓ2)
YB = 30кН
∑MВ = qℓ ℓ/2 + F ℓ2- M - YA (ℓ1 + ℓ2)
YA = 20кН
Проверка: ∑Y= 0
q
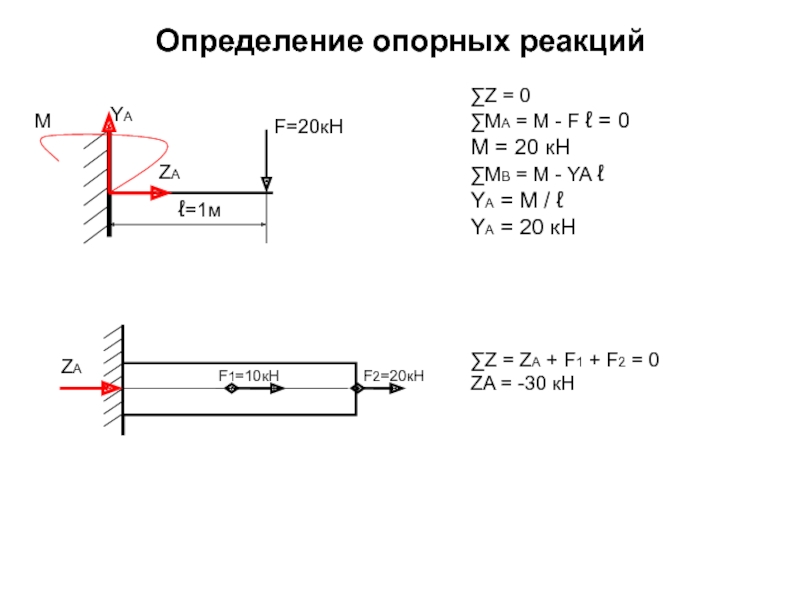
Слайд 26Определение опорных реакций
∑Z = 0
∑MA = M - F ℓ =
M = 20 кН
∑MB = M - YA ℓ
YA = M / ℓ
YA = 20 кН
∑Z = ZA + F1 + F2 = 0
ZA = -30 кН
ZA
F1=10кН
F2=20кН
Слайд 27Виды деформаций
Деформации (изменения размеров и формы тела) возникают под действием нагрузок.
Линейные
Угловые деформации – изменение угловых размеров.
Слайд 28Виды деформаций
S
S
2
1
3
4
2
1
3
4
α
S = ∆S + S
ε = ∆S / S –средняя
α – угловая деформация
Слайд 29Основные допущения о свойствах материалов
материал имеет сплошное (непрерывное) строение;
материал однороден,
материал изотропен, т.е. его свойства во всех направлениях одинаковы;
материал упруг, т.е. после снятия внешних воздействий он полностью восстанавливает свои размеры и форму.
Слайд 30Гипотезы о характере деформаций
гипотеза плоских сечений Бернулли – сечения, плоские и
гипотеза о ненадавливании волокон – волокна могут деформироваться только под действием усилий, направленных вдоль них;
закон Гука – упругие деформации прямо пропорциональны приложенной нагрузке.
Слайд 31Гипотезы о характере деформаций и другие принципы
Гипотеза об отсутствии первоначальных внутренних
Принцип неизменности начальных размеров - деформации малы по сравнению с первоначальными размерами тела.
Принцип независимости действия сил - результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, приложенных к телу последовательно и в любом порядке.
Слайд 32Принцип Сен - Венана
В точках тела достаточно удаленных от места приложения
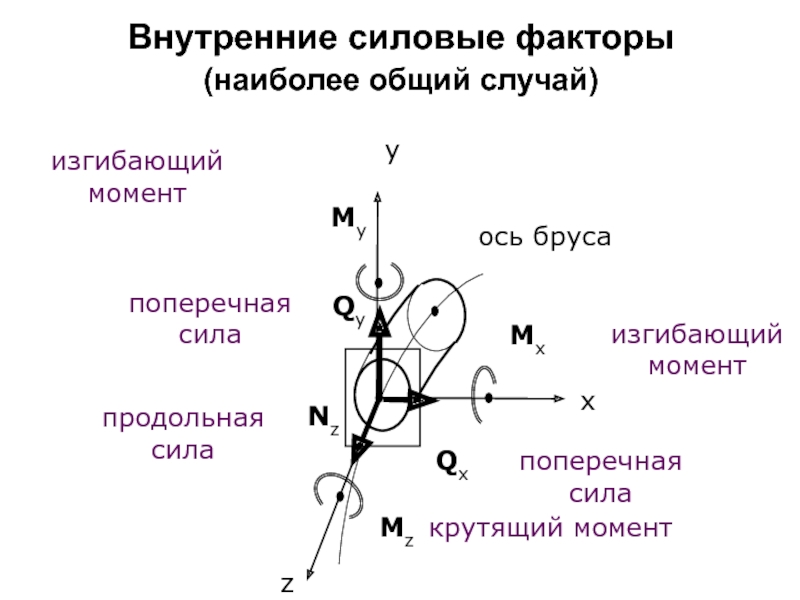
Слайд 34Внутренние силовые факторы
(частные случаи)
Если в сечении под воздействием внешних нагрузок (к
продольная сила Nz – случай нагружения - растяжение (сжатие);
изгибающий момент Мх (Му) –- изгиб (чистый);
поперечная сила Qx (Qy) – сдвиг;
крутящий момент Мz – кручение.
Слайд 35Метод сечений
(для определения внутренних силовых факторов)
Мысленно рассекают брус на две части
Отбрасывают одну из частей и взаимодействие частей друг с другом заменяют внутренними усилиями, которые уравновешивают внешние силы, действующие на отсеченную часть.
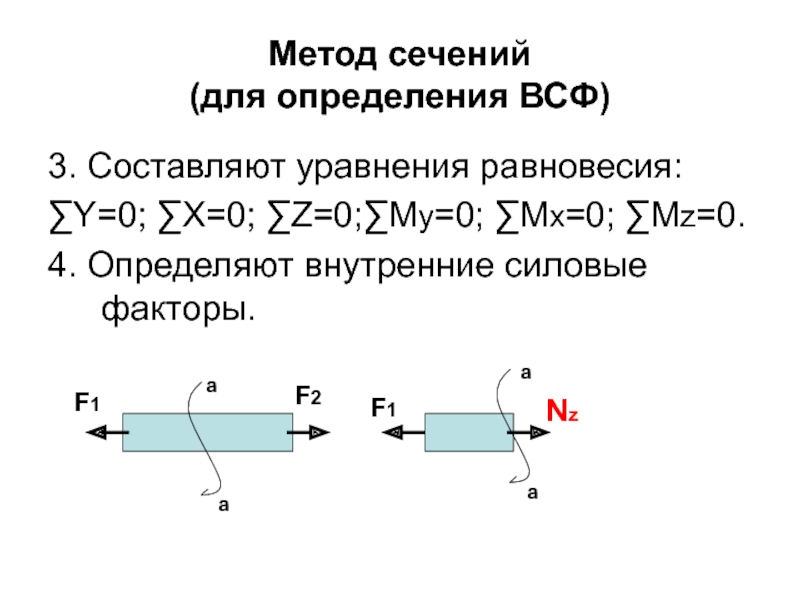
Слайд 36Метод сечений
(для определения ВСФ)
3. Составляют уравнения равновесия:
∑Y=0; ∑X=0; ∑Z=0;∑Мy=0; ∑Мx=0; ∑Мz=0.
4.
F2
F1
F1
Nz
a
a
a
a
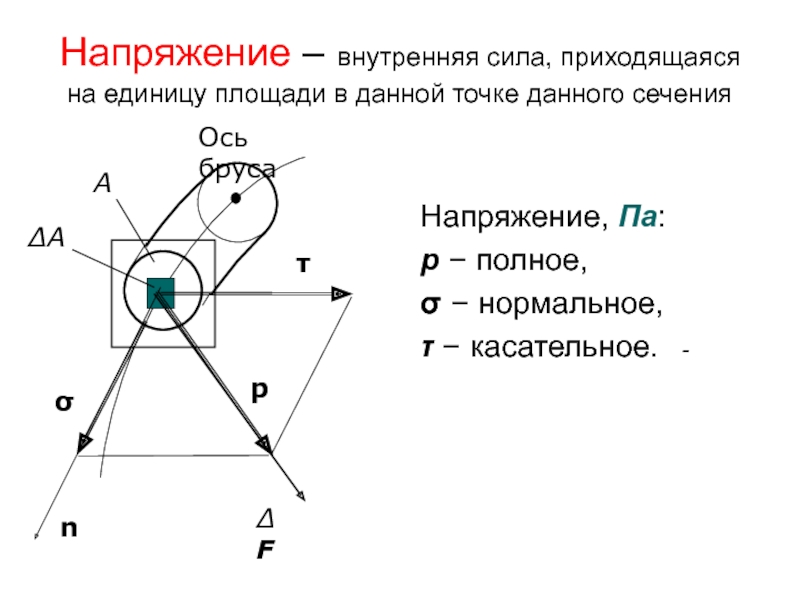
Слайд 37Напряжение – внутренняя сила, приходящаяся на единицу площади в данной точке
Напряжение, Па:
p – полное,
σ – нормальное,
τ – касательное. -
p
τ
σ
n
ΔA
A
ΔF
Ось бруса
Слайд 38Напряжения
Среднее напряжение, приходящееся на единицу площади ∆A:
Рm = ∆F
Уменьшая размеры площадки до предела, получим истинное напряжение или напряжение в данной точке данного сечения:
Р = lim ∆F / ∆A при ∆A→0
Слайд 39Напряженное состояние в данной точке
это совокупность напряжений на всех элементарных площадках,
Рассмотрим элементарный (бесконечно малый) куб, ребра которого параллельны осям координат.
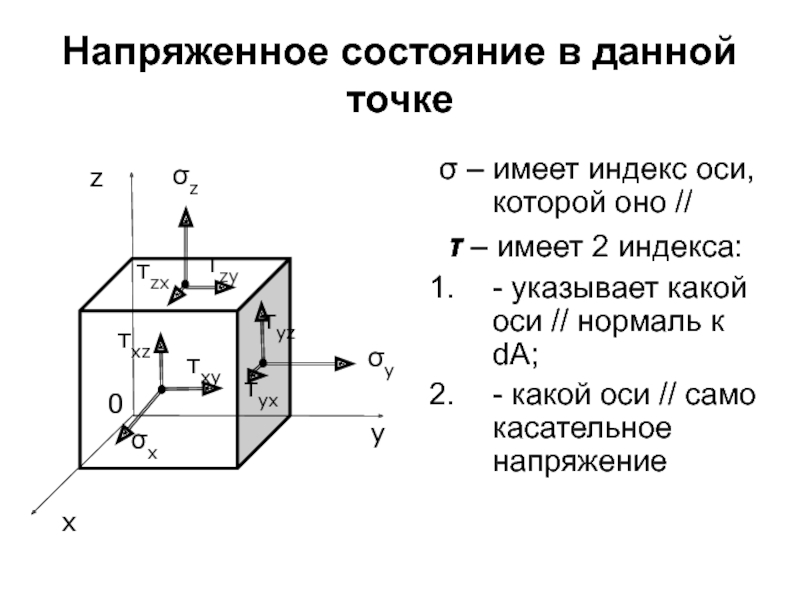
Слайд 40Напряженное состояние в данной точке
σ – имеет индекс оси, которой оно
τ – имеет 2 индекса:
- указывает какой оси // нормаль к dA;
- какой оси // само касательное напряжение
τxz
x
τxy
τyx
τyz
τzx
τzy
σz
σy
σx
z
y
0
Слайд 41Главные площадки и главные напряжения
Главными площадками напряжений называют площадки, на которых
Главные напряжения - нормальные напряжения σ, действующие на главных площадках.(σ1>σ2>σ3 – с учетом знака).
В каждой точке напряженного тела существуют три главные взаимно перпендикулярные площадки.
Слайд 42Виды напряженного состояния
Объемное напряженное состояние: σ1≠0 σ2≠0 σ3≠0.
Плоское напряженное состояние: одно
Линейное напряженное состояние: два главных напряжения = 0.
Условие прочности для простейших случаев: σmax ≤ [σ] τ max ≤ [τ]
Слайд 43Центральное растяжение и сжатие
Центральным растяжением (сжатием) называют вид деформации, при котором
Основные гипотезы: гипотеза о ненадавливании продольных волокон, гипотеза плоских сечений Бернулли, принцип Сен-Венана.
Слайд 44Центральное растяжение и сжатие
гипотеза плоских сечений Бернулли – сечения, плоские и
гипотеза о ненадавливании волокон – волокна могут деформироваться только под действием усилий, направленных вдоль них;
принцип Сен-Венана – в точках тела достаточно удаленных от места приложения нагрузок, внутренние силы мало зависят от конкретного способа приложения этих нагрузок.
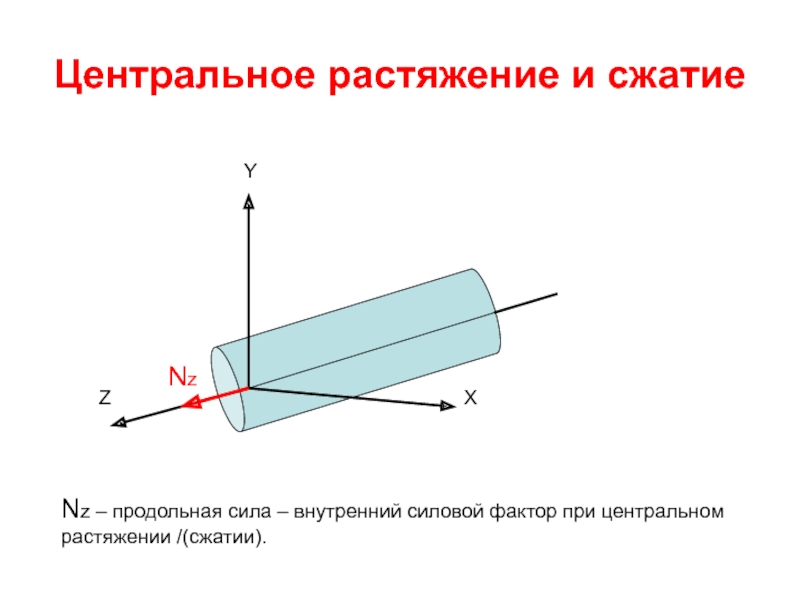
Слайд 45Центральное растяжение и сжатие
Z
Y
X
Nz
Nz – продольная сила – внутренний силовой фактор
растяжении /(сжатии).
Слайд 46Построение эпюры Nz при центральном растяжении (сжатии)
Брус заменяют расчетной схемой, изобразив
Для определения продольной силы Nz используют метод сечений.
При построении эпюры продольных сил брус делят на участки для которых материал однороден; F = const; A = const.
Слайд 47Проверка правильности построения эпюр Nz
Если в сечении проложена сосредоточенная сила, то
Если участок балки находится в состоянии сжатия то продольная сила меньше нуля и наоборот при растяжении она положительна.
При наличии распределенной нагрузки продольная сила изменяется по линейному закону; в противном случае продольная сила постоянна.
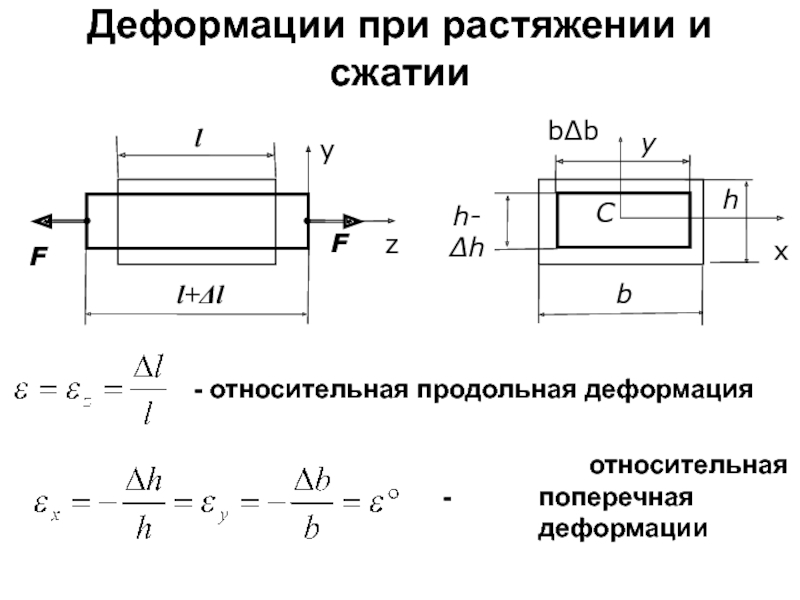
Слайд 48Деформации при растяжении и сжатии
- относительная продольная деформация
bΔb
x
относительная
-
Слайд 49Закон Гука. Коэффициент Пуассона.
- напряжение при растяжении и сжатии, Н/мм2
μ – коэффициент Пуассона, 0≤ μ ≤0,5.
Закон Гука, где Е – модуль продольной упругости (Юнга), Н/мм2 (МПа).
- удлинение стержня
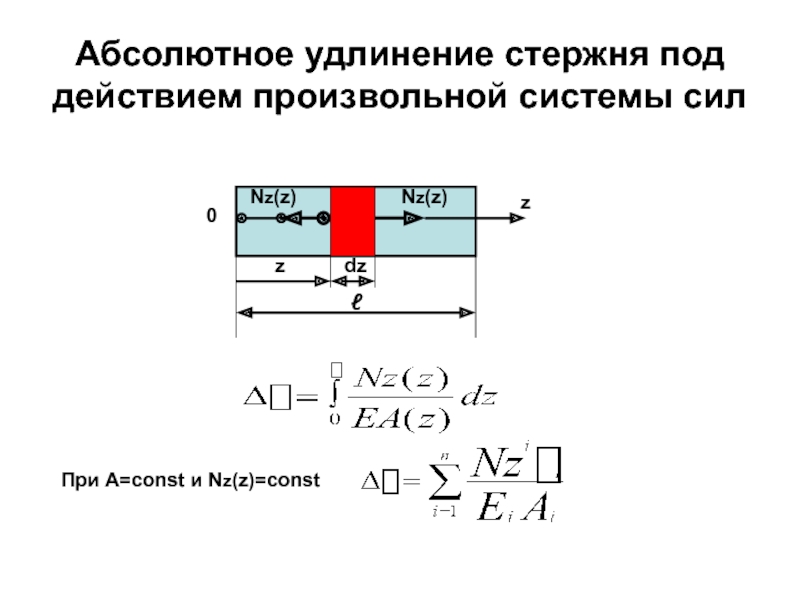
Слайд 50Абсолютное удлинение стержня под действием произвольной системы сил
ℓ
z
dz
z
0
Nz(z)
Nz(z)
При А=const и Nz(z)=const
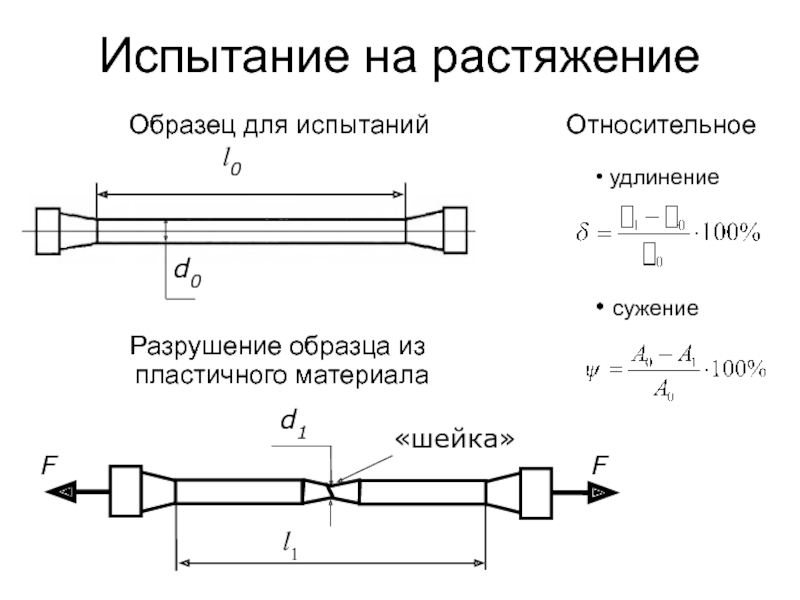
Слайд 51Испытание на растяжение
Разрушение образца из пластичного материала
Образец для испытаний
Относительное
сужение
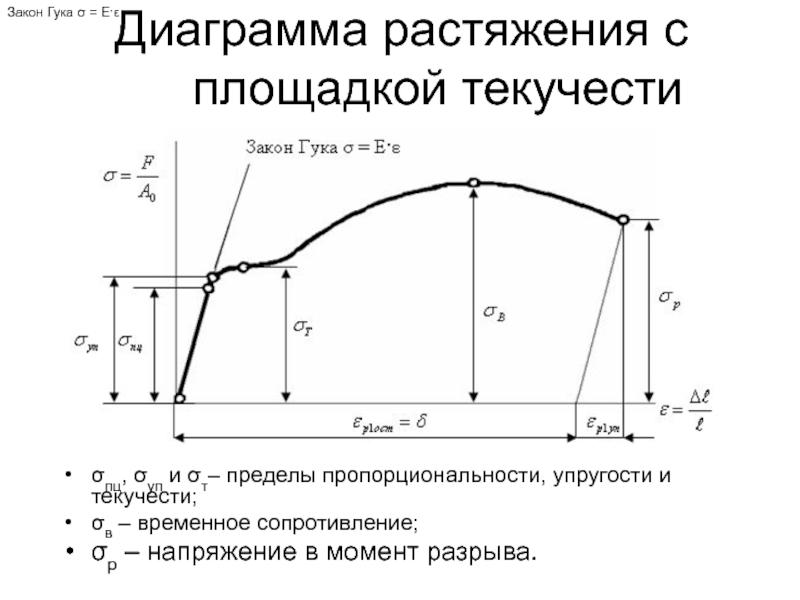
Слайд 52Диаграмма растяжения с площадкой текучести
σпц, σуп и σт– пределы пропорциональности,
σв – временное сопротивление;
σр – напряжение в момент разрыва.
Закон Гука σ = E·ε
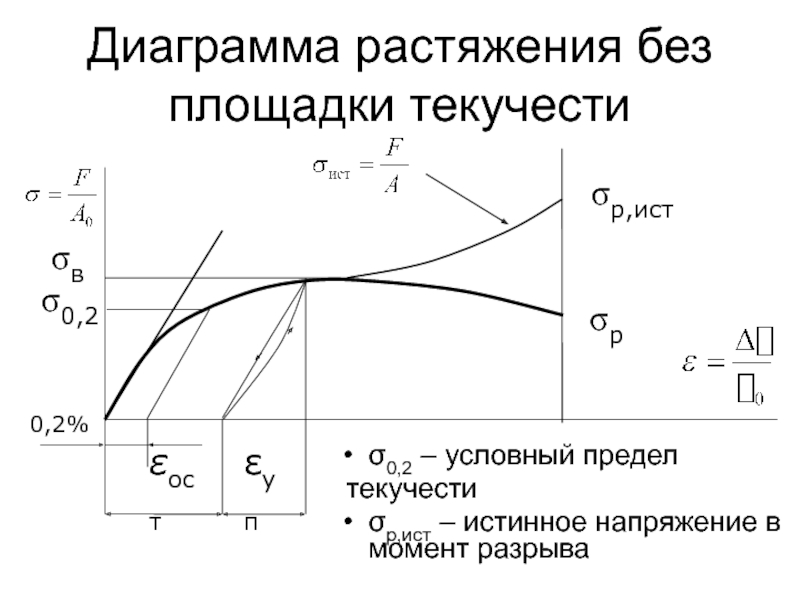
Слайд 53Диаграмма растяжения без площадки текучести
σ0,2 – условный предел
текучести
σр,ист – истинное
εост
εуп
σр,ист
σр
σв
σ0,2
0,2%
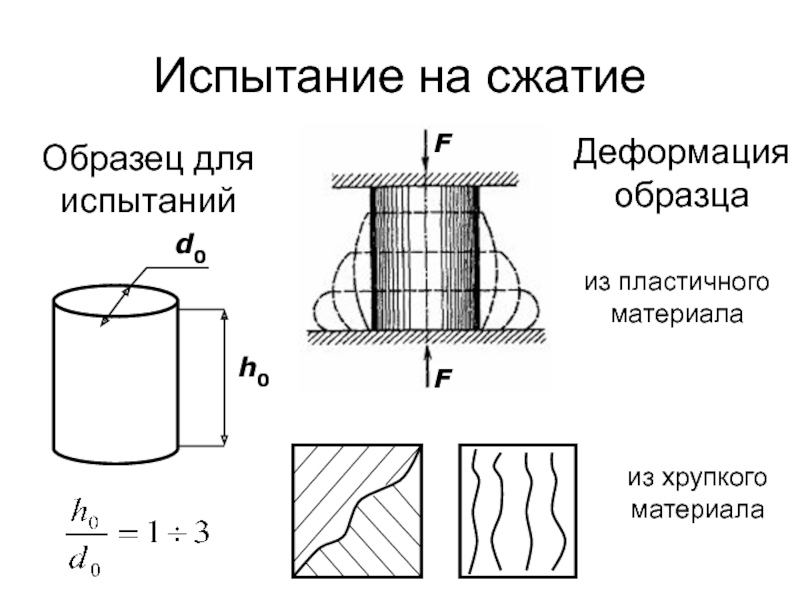
Слайд 54Испытание на сжатие
d0
h0
Образец для испытаний
Деформация образца
из пластичного материала
из хрупкого материала
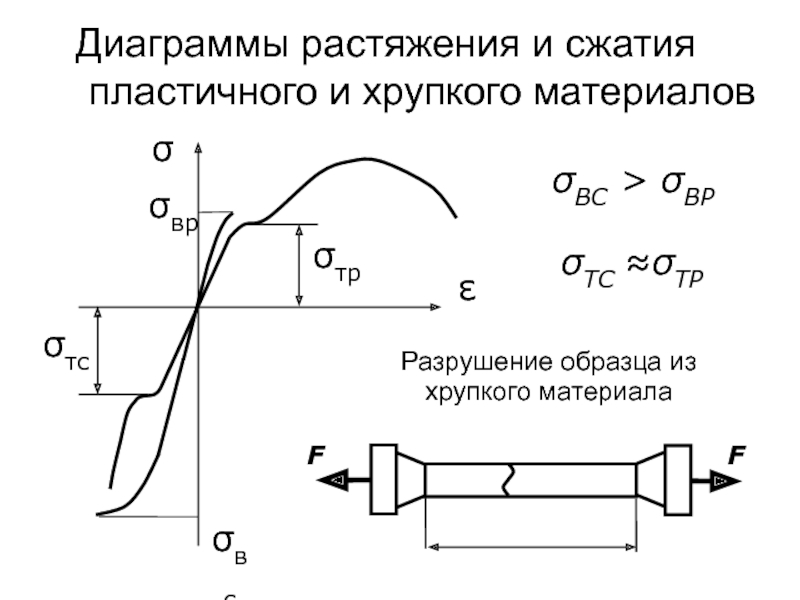
Слайд 55Диаграммы растяжения и сжатия пластичного и хрупкого материалов
ε
σ
σВС > σВР
σвр
F
F
σвс
σтр
σтс
σТС ≈σТР
Слайд 56Расчеты на прочность при растяжении и сжатии
проверочный расчет
проектный расчет
определение
Слайд 57Допускаемые напряжения и коэффициент запаса прочности
- допускаемое напряжение
- предельное (опасное)
- для пластических материалов
- для хрупких материалов
- коэффициент запаса прочности
,
- для пластических материалов
- для хрупких материалов
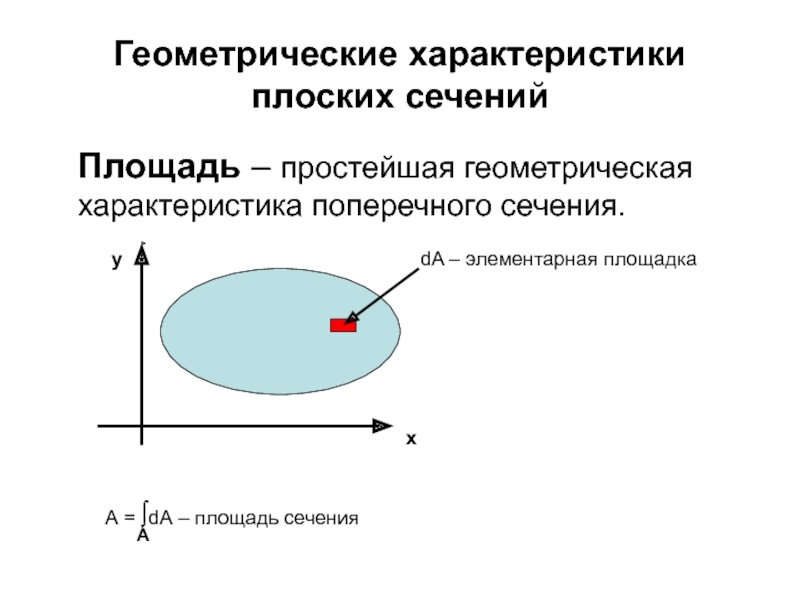
Слайд 58Геометрические характеристики плоских сечений
Площадь – простейшая геометрическая характеристика поперечного
dA – элементарная площадка
А = ∫dА – площадь сечения
А
y
x
Слайд 59Геометрические характеристики плоских сечений
В расчетах элементов конструкций (на изгиб, кручение,
статический осевой момент;
осевой момент инерции;
полярный момент инерции;
центробежный момент инерции.
Эти характеристики учитывают не только форму и размер сечения, но и расположение точек и осей относительно которых они вычисляются
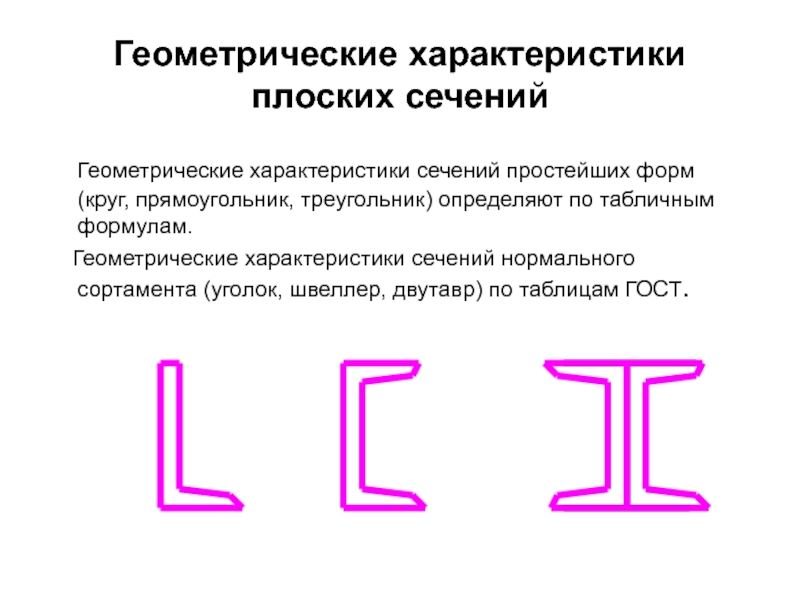
Слайд 60Геометрические характеристики плоских сечений
Геометрические характеристики сечений простейших форм (круг,
Геометрические характеристики сечений нормального сортамента (уголок, швеллер, двутавр) по таблицам ГОСТ.
Слайд 61Статический момент сечения
Статический момент инерции относительно некоторой оси – взятая
Sx = = ∫ydА Sy = = ∫xdА
A
A
На основании теоремы о моменте равнодействующей можно показать, что:
Sx = Ayc ; Sy = Axc , где yc , xc - координаты центра тяжести сечения.
Статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно этой же оси.
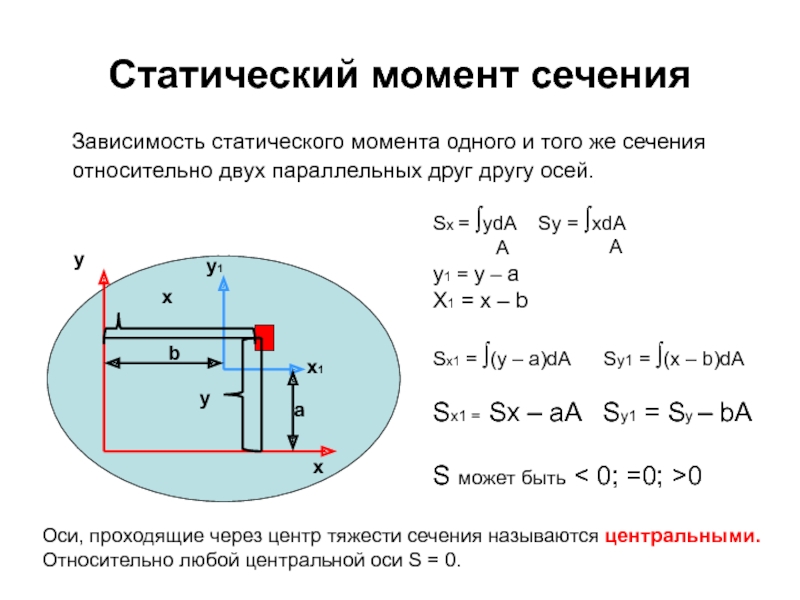
Слайд 62 Зависимость статического момента одного и того же сечения относительно
Статический момент сечения
y
y1
x1
x
y
x
a
b
Sx = ∫ydA Sy = ∫xdA
y1 = y – a
X1 = x – b
Sx1 = ∫(y – a)dA Sy1 = ∫(x – b)dA
Sx1 = Sx – aA Sy1 = Sy – bA
S может быть < 0; =0; >0
A
A
Оси, проходящие через центр тяжести сечения называются центральными.
Относительно любой центральной оси S = 0.
Слайд 63Осевой момент инерции
Осевой момент инерции сечения – взятая по всей
или
Осевым моментом инерции сечения называется геометрическая характеристика, численно равная интегралу:
oотносительно оси x
Ix = ∫ y²dA
относительно оси y
Iy = ∫ x²dA
А
А
Слайд 64Полярный момент инерции
Полярный момент инерции относительно некоторой точки –
или
Полярным моментом инерции сечения называется геометрическая характеристика, определяемая интегралом вида:
Iρ = ∫ ρ²dA
Iρ = Ix + Iy
А
Слайд 65Центробежный момент инерции
Центробежный момент инерции сечения относительно 2-х
или
Центробежным моментом инерции называется геометрическая характеристика, определяемая интегралом вида:
Ixy = ∫ xydA
A
Слайд 66Главные оси сечения
Для главных осей сечения должны выполняться
Центробежный момент инерции сечения относительно этих осей должен быть равен нулю: Ixy = 0
Осевые моменты инерции относительно этих осей должны быть экстремальны.
Эти оси должны быть взаимно перпендикулярны.
Главные центральные оси – главные оси, проходящие через центр тяжести сечения.
Слайд 67Главные оси сечения
Относительно главных центральных осей сечения:
Ixy = 0
Ix
Sx = 0 и Sy = 0
Ix + Iy = Iρ - сумма осевых моментов сечения относительно 2-х взаимно перпендикулярных осей равна полярному моме5нту инерции этого сечения относительно точки пересечения этих осей
Слайд 68Определение моментов инерции простых фигур
0 – центр тяжести сечения; x II b
dA = bdy
Ix = ∫y²dA = ∫y²bdy = by³/2
dy
h
b
y
x
A
h/2
h/2
-h/2
h/2
-h/2
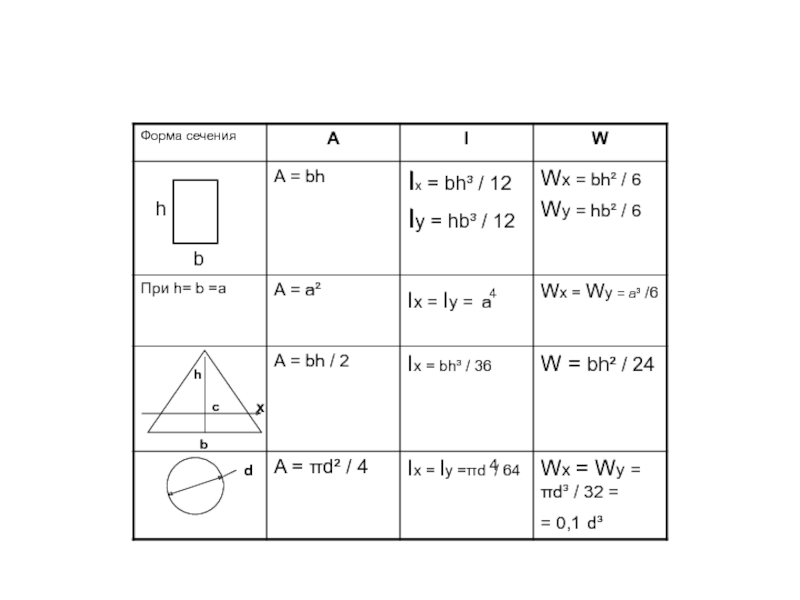
Ix = bh³ /12 Iy = hb³ /12
Слайд 69Зависимость между моментами инерции относительно параллельных осей
Момент инерции относительно любой оси
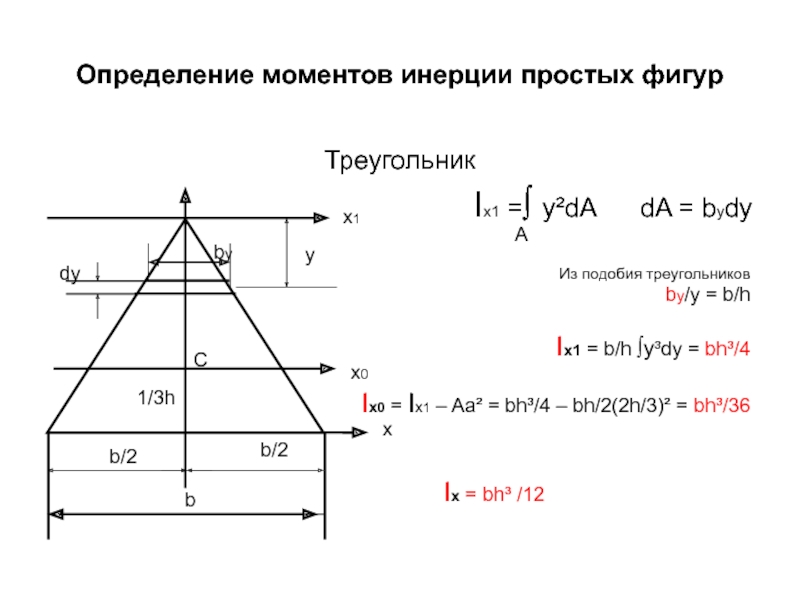
Слайд 70Определение моментов инерции простых фигур
Треугольник
A
Из подобия треугольников
by/y = b/h
Ix1 = b/h ∫y³dy = bh³/4
Ix0 = Ix1 – Aa² = bh³/4 – bh/2(2h/3)² = bh³/36
Ix = bh³ /12
Слайд 71Определение моментов инерции простых фигур
Круг
y
x
Iρ = ∫ ρ²dA
Iρ = 2π∫ ρ³dρ = πr /2 = πd /32 ≈ 01d
Ix0 = Iy0 = Iρ/2 = πr /4 = πd /64 ≈ 0,05d
Дkя кольца: Ix0 = Iy0 = 0,05D (1 – c ),
где с = d /D
Слайд 74ИЗГИБ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ГИПОТЕЗЫ.
Изгиб – вид деформации, при котором искривляется
Прямой изгиб – изгиб, при котором внешние силы, действующие на балку, лежат в одной (силовой) плоскости, проходящей через продольную ось балки и главную центральную ось инерции поперечного сечения.
Слайд 75ИЗГИБ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ГИПОТЕЗЫ.
Чистый изгиб – в любом поперечном сечении
Поперечный изгиб – в поперечном сечении балки одновременно действуют изгибающий момент М и поперечная сила Q.
Слайд 76
ИЗГИБ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ГИПОТЕЗЫ
гипотеза плоских сечений Бернулли – сечения, плоские
гипотеза о ненадавливании волокон – волокна могут деформироваться только под действием усилий, направленных вдоль них.
Слайд 78Определение внутренних силовых факторов при изгибе
Для определения ВСФ
В поперечном сечении Q – численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от сечения.
М – численно равен алгебраической сумме моментов внешних сил, действующих по одну сторону от сечения.
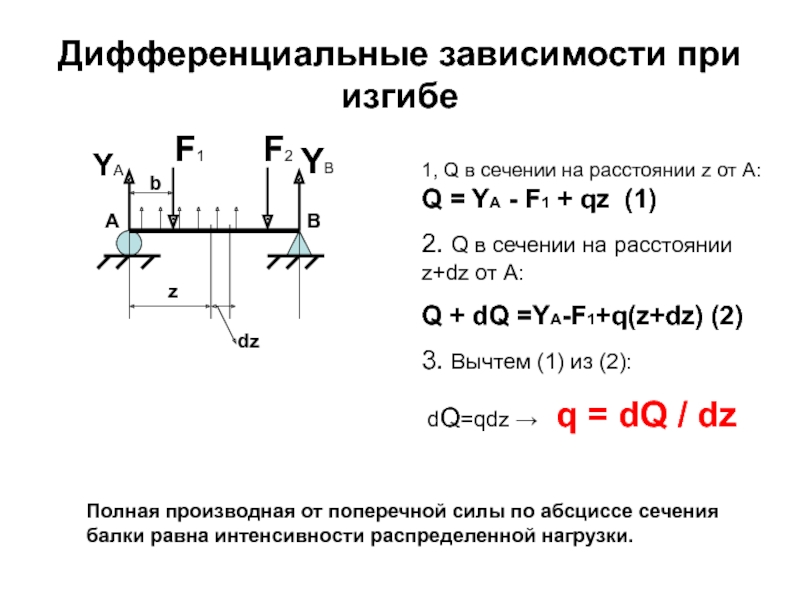
Слайд 80Дифференциальные зависимости при изгибе
YA
YB
b
z
dz
F1
F2
1, Q в сечении на расстоянии z от
2. Q в сечении на расстоянии z+dz от А:
Q + dQ =YA-F1+q(z+dz) (2)
3. Вычтем (1) из (2):
dQ=qdz → q = dQ / dz
A
B
Полная производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.
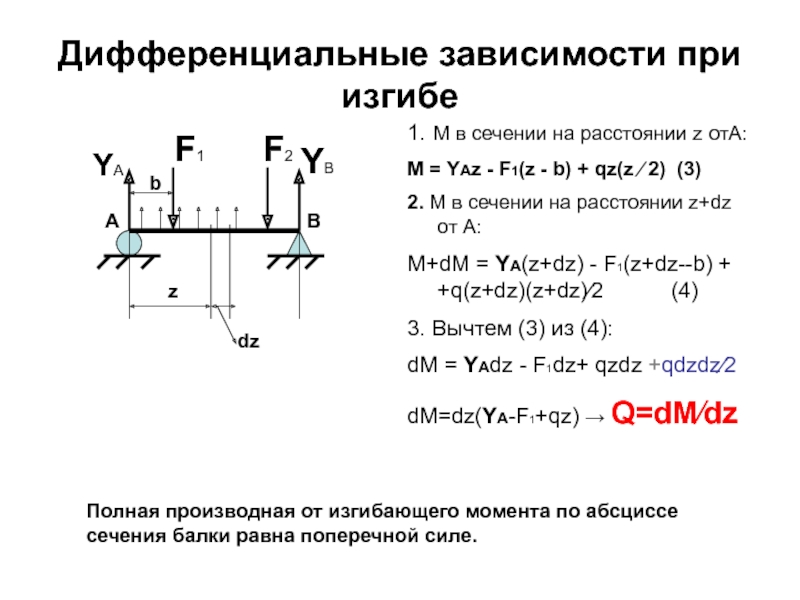
Слайд 81Дифференциальные зависимости при изгибе
YA
YB
b
z
dz
F1
F2
1. М в сечении на расстоянии z отА:
M
2. М в сечении на расстоянии z+dz от А:
M+dM = YA(z+dz) - F1(z+dz--b) + +q(z+dz)(z+dz)⁄2 (4)
3. Вычтем (3) из (4):
dM = YAdz - F1dz+ qzdz +qdzdz⁄2
dM=dz(YA-F1+qz) → Q=dM⁄dz
A
B
Полная производная от изгибающего момента по абсциссе сечения балки равна поперечной силе.
Слайд 82Дифференциальные зависимости при изгибе
Вторая производная от изгибающего момента равна интенсивности распределенной
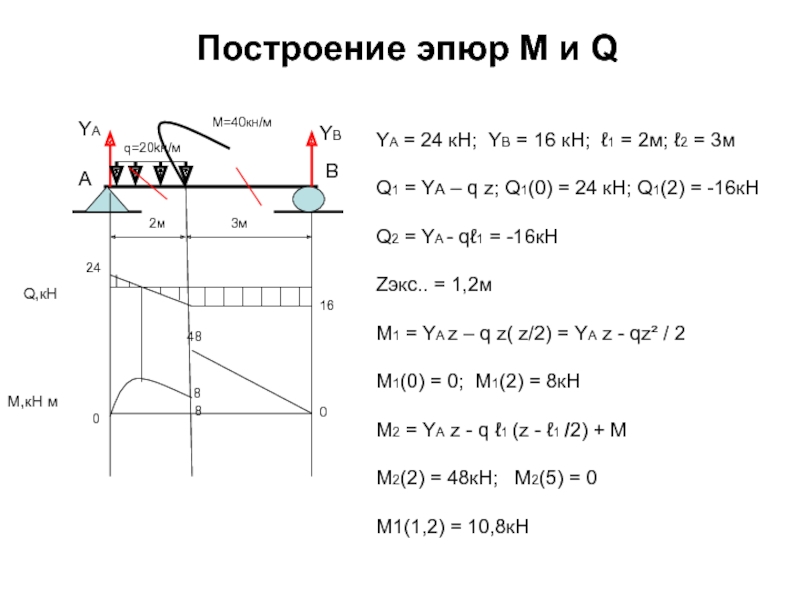
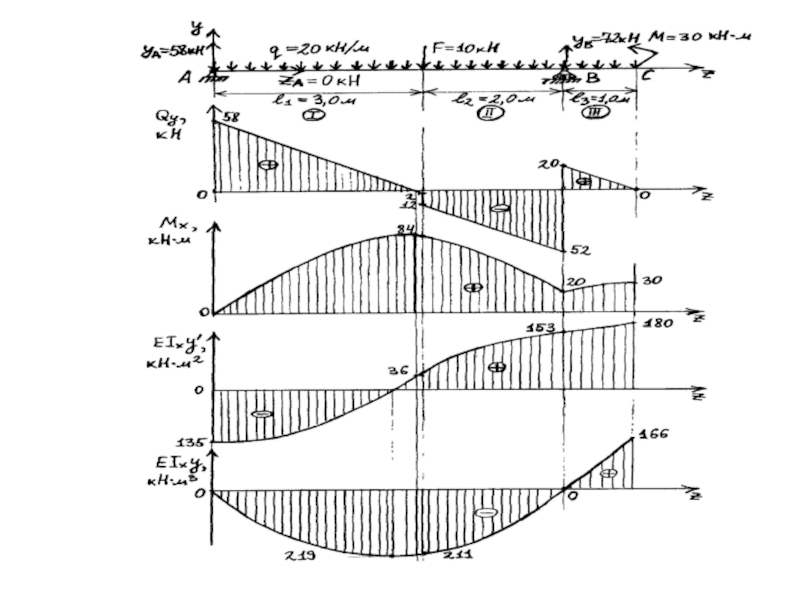
Слайд 83Построение эпюр М и Q
YA
3м
YA = 24 кН; YB = 16
Q1 = YA – q z; Q1(0) = 24 кН; Q1(2) = -16кН
Q2 = YA - qℓ1 = -16кН
Zэкс.. = 1,2м
М1 = YA z – q z( z/2) = YA z - qz² / 2
M1(0) = 0; M1(2) = 8кН
М2 = YA z - q ℓ1 (z - ℓ1 /2) + M
M2(2) = 48кН; M2(5) = 0
M1(1,2) = 10,8кН
А
В
8
0
Слайд 84Построение эпюры Nz при центральном растяжении (сжатии)
q= 10кН / м; F1
∑Z = ZA + q(ℓ1 + ℓ2)–F1 - F2 = 0
ZA = 10кН
NZ1 + ZA + qz = 0
NZ1(Z = 0) = - 10кН
NZ1(Z=2) = - 30кН
NZ2 + qz – F1 +ZA= 0
NZ2 (Z = 2) = - 20кН
NZ2 (Z = 4) = - 40 кН
Слайд 85Проверка правильности построения эпюр Q и М
В месте приложения сосредоточенной силы
В месте приложения сосредоточенного изгибающего момента М на эпюре Мx (My) имеет место скачок равный по величине этому моменту (в том числе на концах балки).
Если на конце балки не приложен сосредоточенный изгибающий момент или этот к5онец балки не в жесткой заделке, то Мx (Мy) = 0.
Если поперечная сила Qx (Qy) в сечении отсутствует, то Mx (My) = const.
Если на элюре QX (Qy) меняет знак на противоположны й (т.е. эпюра проходит через 0, то в этой точке эпюра Мx (My) имеет экстремум.
Слайд 86Участку балки с распределенной нагрузкой q соответствует эпюра Qx (Qy), изменяющаяся
Если на эпюре Qx (Qy) имеет место скачок, то на эпюре Mx (My) – перелом графика, т.е. в случае параболы нет общей касательной к сопредельным участкам.
Если эпюра, Q >0, то эпюра M возрастает, а если эпюра Q< 0, то эпюра M убывает.
Если эпюра Q возрастает, то эпюра М имеет прогиб вниз если эпюра Q убывает , то эпюра М имеет прогиб вверх
Проверка правильности построения эпюр Q и М
Слайд 87Определение нормальных напряжений при изгибе
Допущения: гипотеза плоских сечений и гипотеза о
Нейтральный слой – слой балки не испытывающий при изгибе ни растяжения, ни сжатия.
Нейтральная линия (ось) – линия пересечения нейтрального слоя с плоскостью сечения балки.
ρ – радиус кривизны нейтрального слоя балки
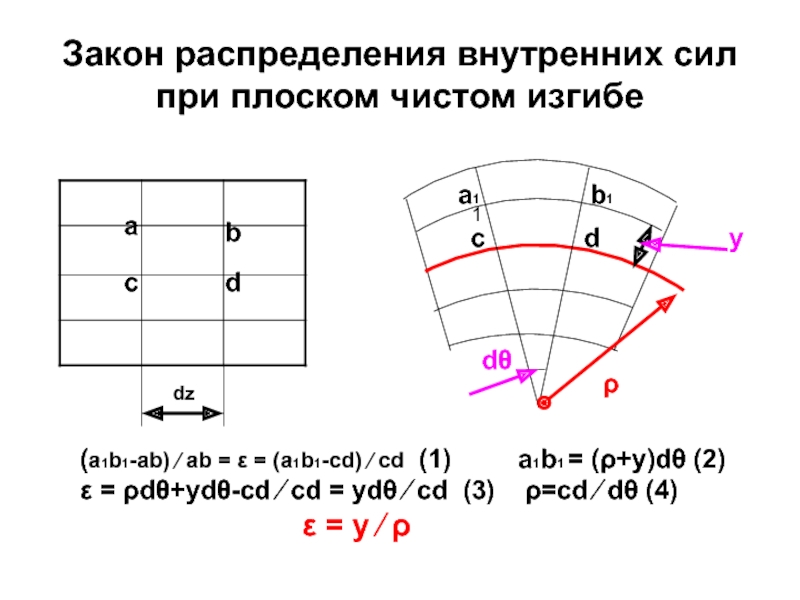
Слайд 88Закон распределения внутренних сил при плоском чистом изгибе
dz
a
b
c
d
c
d
1
a1
b1
ρ
у
dθ
(a1b1-ab) ⁄ ab =
ε = ρdθ+уdθ-cd ⁄ cd = уdθ ⁄ cd (3) ρ=cd ⁄ dθ (4)
ε = у ⁄ ρ
Слайд 89Закон распределения внутренних сил при плоском чистом изгибе
По высоте сечения балки
ε = у ⁄ ρ
Нормальные напряжения изменяются по высоте поперечного сечения балки пропорционально расстоянию от нейтральной оси.
σ = Еε = Еу ⁄ ρ
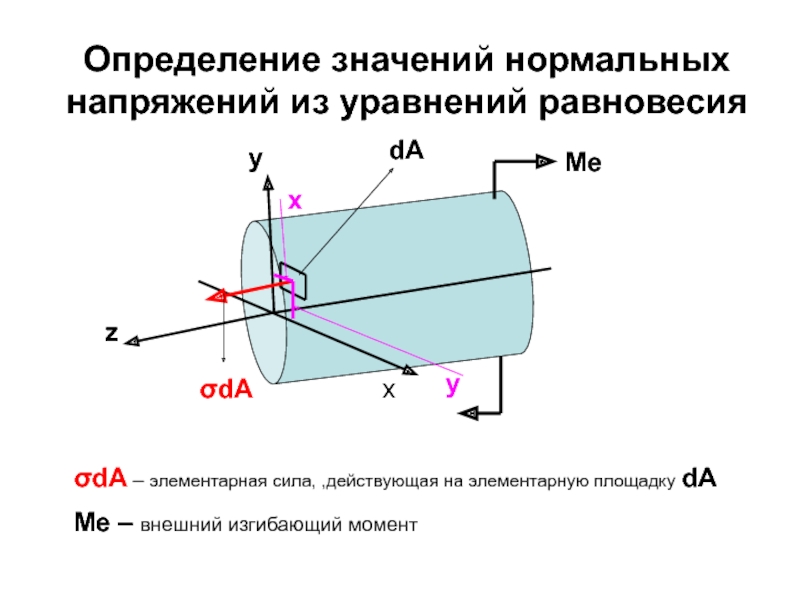
Слайд 90Определение значений нормальных напряжений из уравнений равновесия
dA
σdA
у
x
σdA – элементарная сила, ,действующая
Me – внешний изгибающий момент
Me
у
z
x
Слайд 91Определение значений нормальных напряжений из уравнений равновесия
Если часть балки, находящаяся под
1. ∑X=0 2. ∑Y=0 3. ∑Z=0
4. ∑Mx=0 5. ∑Mу=0 6. ∑Mz=0
Слайд 92Определение значений нормальных напряжений из уравнений равновесия
Уравнения №1 и №2 –
Из уравнения №3:
(σ=Eу ⁄ ρ)
Нейтральная ось проходит через центр тяжести поперечного сечения.
Слайд 93Определение значений нормальных напряжений из уравнений равновесия
Из уравнения 4:
σ=Eу ⁄ ρ
М
1 ⁄ ρ – кривизна нейтрального слоя балки.
σ – нормальное напряжение в произвольной точке сечения.
- жесткость балки
Слайд 94Определение значений нормальных напряжений из уравнений равновесия
Из уравнения 5:
σ=Eу ⁄ ρ
Следовательно
Уравнение №6 - тождество т.к. усилия σdA // оси Z (т. е. нет кручения).
Слайд 95Расчеты на прочность при изгибе
проверочный расчет
проектный расчет
определение допускаемой
Слайд 96Касательные напряжения при изгибе
Формула Журавского (для прямого изгиба):
Касательное напряжение в рассматриваемом
Q – поперечная сила; b – ширина рассматриваемого волокна;
- статический момент «отсеченной площади» сечения (лежащей дальше от нейтральной линии, чем рассматриваемый слой волокна
- момент инерции всего сечения относительно нейтральной оси
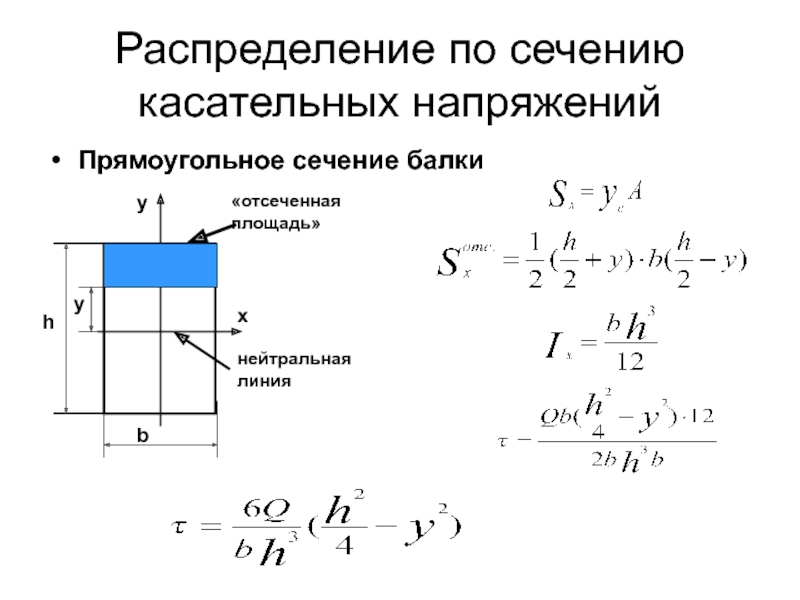
Слайд 97Распределение по сечению касательных напряжений
Прямоугольное сечение балки
у
x
b
h
«отсеченная площадь»
нейтральная линия
у
Слайд 99Определение перемещений в балках постоянного сечения методом непосредственного интегрирования
Под действием внешних
Упругая линия – изогнутая ось балки.
Прогиб балки в данной точке (сечении) – перемещение центра тяжести сечения по направлению, перпендикулярному оси балки.
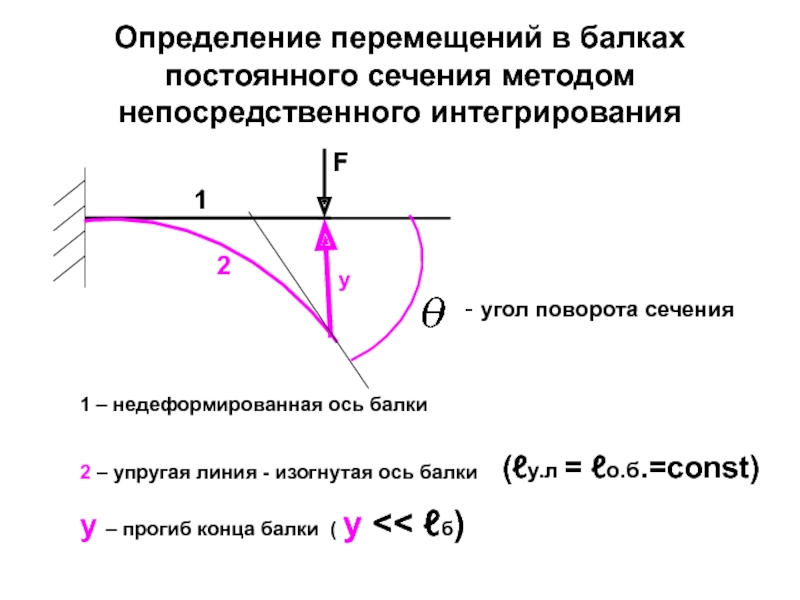
Слайд 100Определение перемещений в балках постоянного сечения методом непосредственного интегрирования
F
y
1
2
1 – недеформированная
2 – упругая линия - изогнутая ось балки
y – прогиб конца балки ( y << ℓб)
- угол поворота сечения
(ℓу.л = ℓо.б.=const)
Слайд 101Определение перемещений в балках постоянного сечения методом непосредственного интегрирования
Угол поворота поперечного
>0, если поперечное сечение при деформации поворачивается против часовой стрелки
Слайд 102Определение перемещений в балках постоянного сечения методом непосредственного интегрирования
Правило знаков для
y>0, если точки оси смещаются при деформации вверх относительно недеформированной оси балки.
Смещениями точек оси по горизонтали (сдвигами) пренебрегают, так как они весьма малы.
Слайд 103Определение перемещений в балках постоянного сечения методом непосредственного интегрирования
Из курса математического
Кривизна изогнутой оси балки:
Слайд 104Дифференциальное уравнение упругой линии балки при изгибе
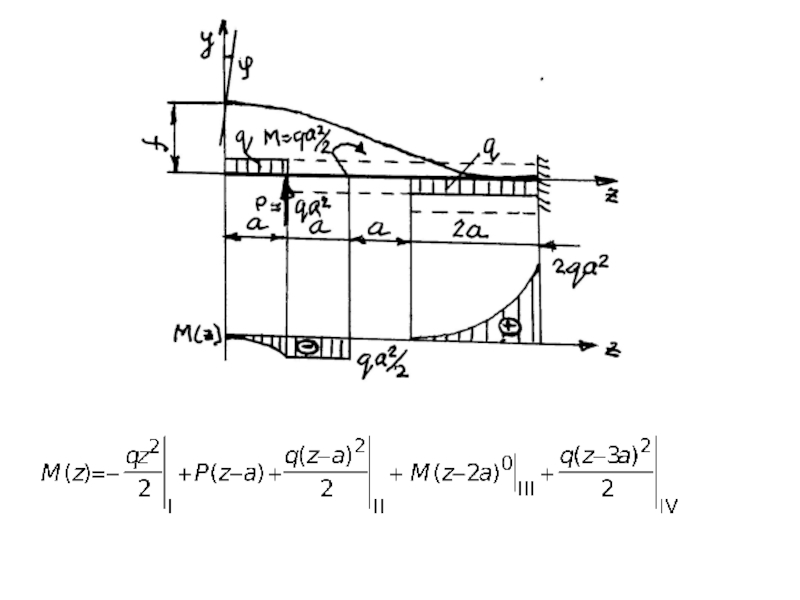
Величину прогиба y (z) находят
Слайд 105Дифференциальное уравнение упругой линии балки при изгибе
- угол поворота поперечного сечения
Величину углов поворота поперечных сечений балки находят интегрированием дифференциального уравнения упругой линии балки с учетом граничных условий рассматриваемой задачи.
Слайд 106Дифференциальное уравнение упругой линии балки при изгибе
- уравнение изгибающих моментов
- уравнение
- уравнение прогибов
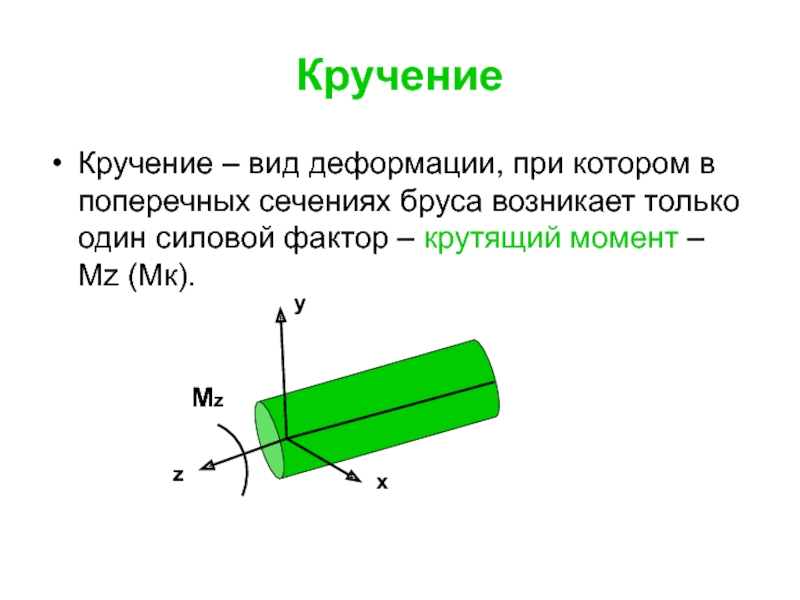
Слайд 110Кручение
Кручение – вид деформации, при котором в поперечных сечениях бруса возникает
y
x
z
Mz
Слайд 111Кручение
Кручение прямого бруса происходит при нагружении его внешними скручивающими моментами (парами
Если прямой брус находится в состоянии покоя или равномерного вращения, то алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу = 0.
Слайд 112Кручение
Крутящие моменты, возникающие в поперечных сечениях бруса, определяют по внешним скручивающим
Крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме скручивающих моментов, приложенных к брусу по одну сторону от сечения.
Слайд 113Кручение
Изменение крутящих моментов по длине бруса выражают графически с помощью эпюры
В сечении, где к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину = значению этого момента.
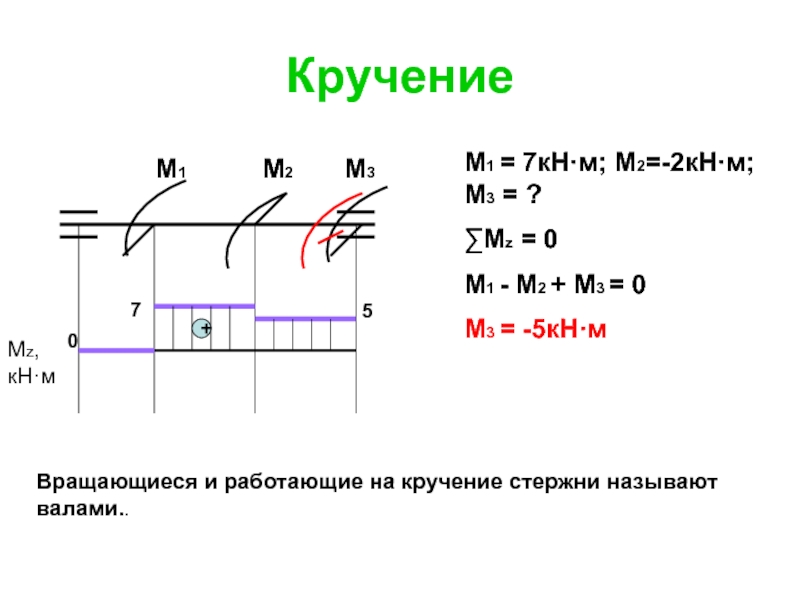
Слайд 116Кручение
М3
М1 = 7кН·м; М2=-2кН·м; М3 = ?
∑Мz = 0
М1 - М2
М3 = -5кН·м
М1
М2
Мz, кН·м
+
Вращающиеся и работающие на кручение стержни называют валами..
7
5
0
Слайд 117Кручение
+
+
Mz, кН
М1
М2
М3
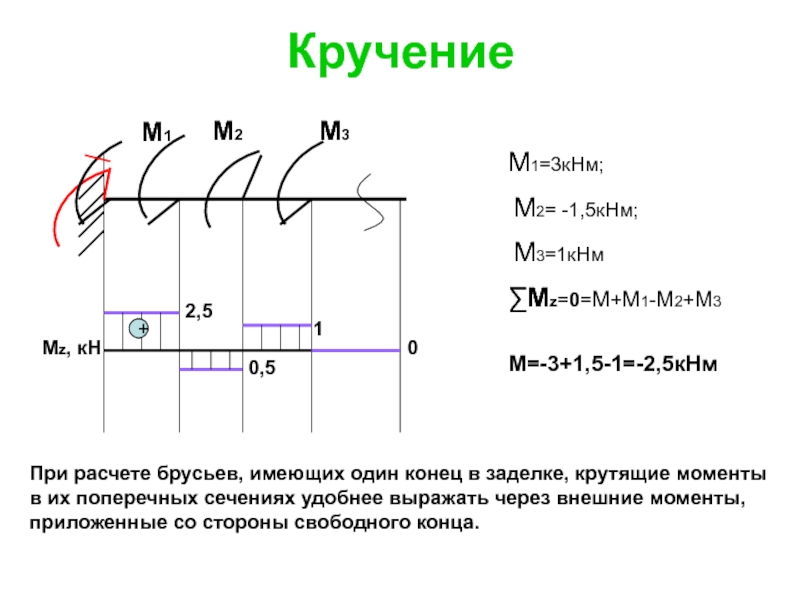
М1=3кНм;
М2= -1,5кНм;
М3=1кНм
∑Мz=0=М+М1-М2+М3
М=-3+1,5-1=-2,5кНм
2,5
0,5
1
0
При расчете брусьев, имеющих один конец
Слайд 118Расчет на прочность при кручении
В поперечном сечении скручиваемого стержня действуют непрерывно
Слайд 119Подбор круглого сечения стержня по полярному моменту сопротивления сечения
Для круга:
- зависит
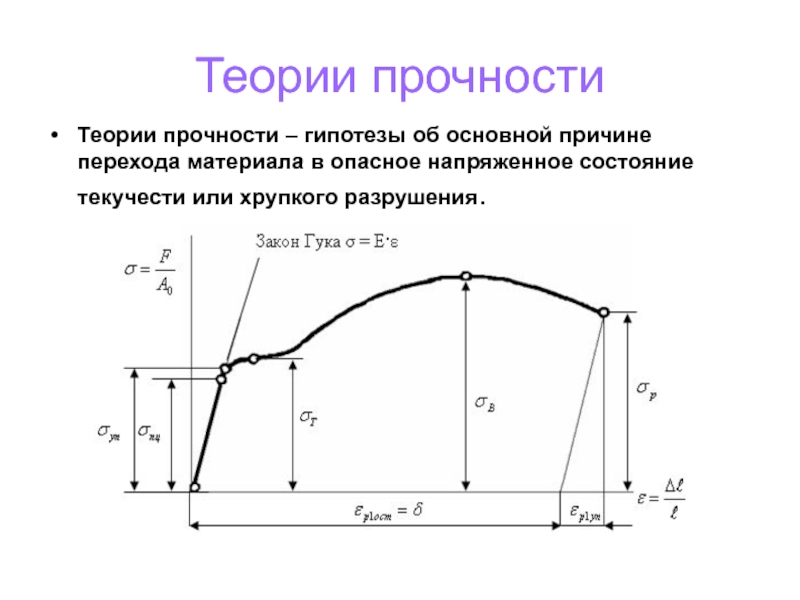
Слайд 120Теории прочности
Теории прочности – гипотезы об основной причине перехода материала в
Слайд 121Составление условия прочности для линейного напряженного состояния
- условие прочности при растяжении
- предельное напряжение для хрупких материалов
- предельное напряжение для пластичных материалов
-устанавливают опытным путем
и
- допускаемое напряжение
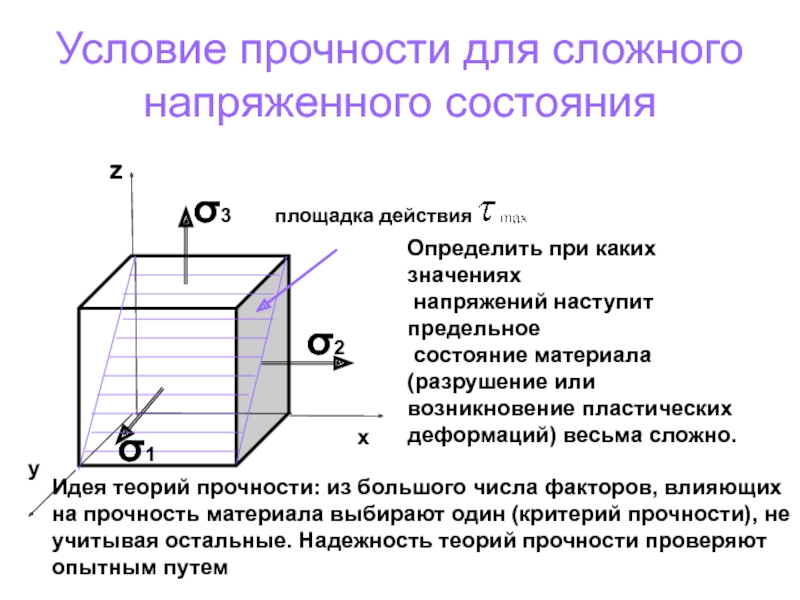
Слайд 122Условие прочности для сложного напряженного состояния
σ1
σ2
σ3
площадка действия
Определить при каких значениях
состояние материала (разрушение или
возникновение пластических деформаций) весьма сложно.
Идея теорий прочности: из большого числа факторов, влияющих на прочность материала выбирают один (критерий прочности), не учитывая остальные. Надежность теорий прочности проверяют опытным путем
z
y
x
Слайд 123Эквивалентное напряжение
- напряжение, при котором образец материала в условиях одноосного напряженного
Опасная точка – точка бруса, в которой достигается максимальное значение эквивалентного напряжения. Эта точка принадлежит опасному сечению бруса.
Слайд 124Первая теория прочности
(теория наибольших нормальных напряжений)
Предельное состояние материала при сложном напряженном
Теория удовлетворительно справедлива для хрупких материалов; частично подтверждается опытным путем; в практических расчетах не применяется.
Слайд 125Вторая теория прочности (теория относительных удлинений)
Опасное состояние материала наступает тогда, когда
Экспериментально теория не подтверждается
Слайд 126Третья теория прочности (теория наибольших касательных напряжений)
Опасное состояние материала наступает тогда,
Предпосылка создания теории: пластическая деформация в металлах возникает в результате необратимых сдвигов в кристаллической решетке. Наибольшие касательные напряжения имеют место в сечениях, расположенных под углом 45 к направлению главных напряжений σ1 и σ3.
Слайд 127Третья теория прочности (теория наибольших касательных напряжений)
В наклонном сечении при растяжении
При линейном напряженном состоянии:
Тогда по 3 теории прочности, условие прочности при которой:
Слайд 128Третья теория прочности (теория наибольших касательных напряжений)
Формула для определения главных нормальных
Подставим (1); (2) и (3) в (4):
Теория подтверждается экспериментально для пластичных материалов.
Слайд 129Четвертая теория прочности (энергетическая)
Прочность материала при сложном напряженном состоянии обеспечивается в
Потенциальная энергия деформации это величина равная работе внутренних сил, но с противоположным знаком. Потенциальную энергию, отнесенную к единице объема, называют удельной потенциальной энергией.
Слайд 130Четвертая теория прочности (энергетическая)
Теория подтверждается экспериментально для пластичных материалов, так как
Слайд 131Сложное сопротивление
Сложное сопротивление – совместное действие на брус нескольких простых видов
Сочетание деформаций изгиба и кручения характерно для работы валов машин. При расчетах валов учитывают касательные напряжения от изгибающих и крутящих моментов, пренебрегая сравнительно малыми касательными напряжениями от поперечных сил.
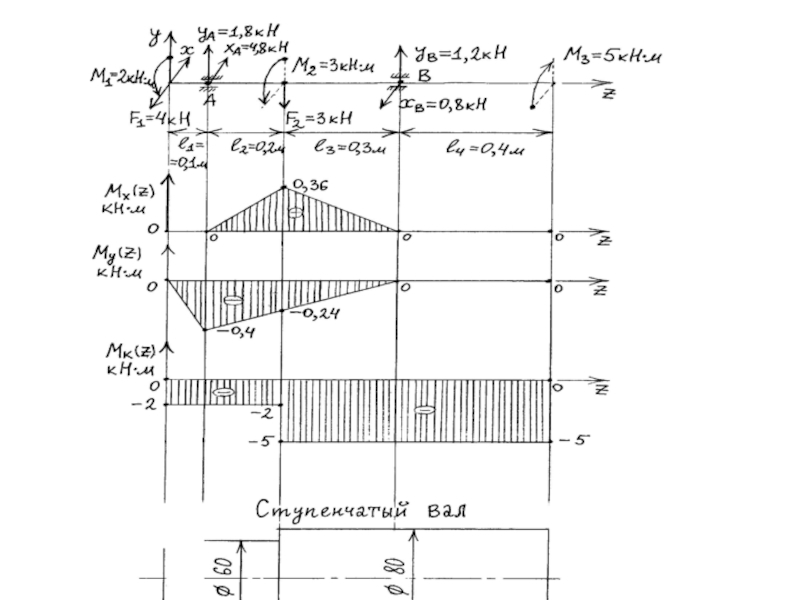
Слайд 133Определение суммарного изгибающего момента:
Определение эквивалентного момента:
Определение диаметров валов по участкам:
, где
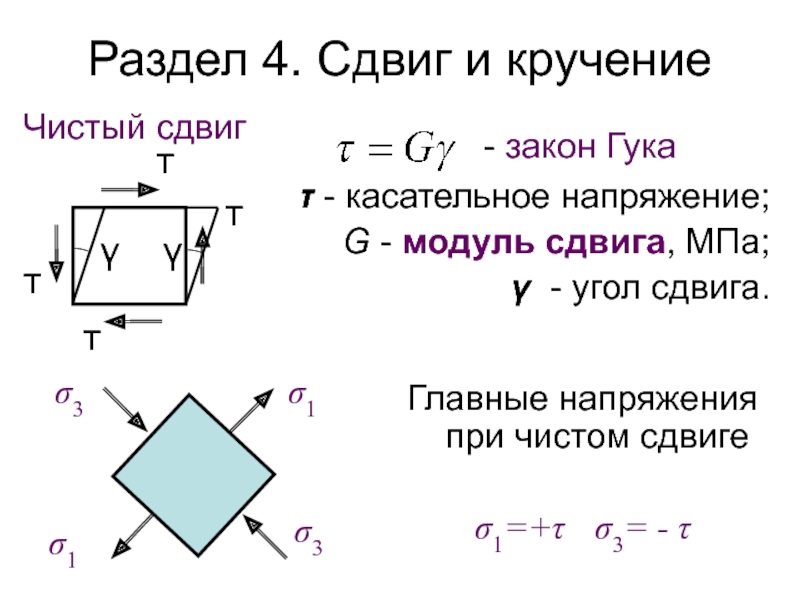
Слайд 135Раздел 4. Сдвиг и кручение
Чистый сдвиг
- закон Гука
τ - касательное
G - модуль сдвига, МПа;
γ - угол сдвига.
σ3
σ1
σ1
σ3
Главные напряжения при чистом сдвиге
σ1=+τ σ3= - τ
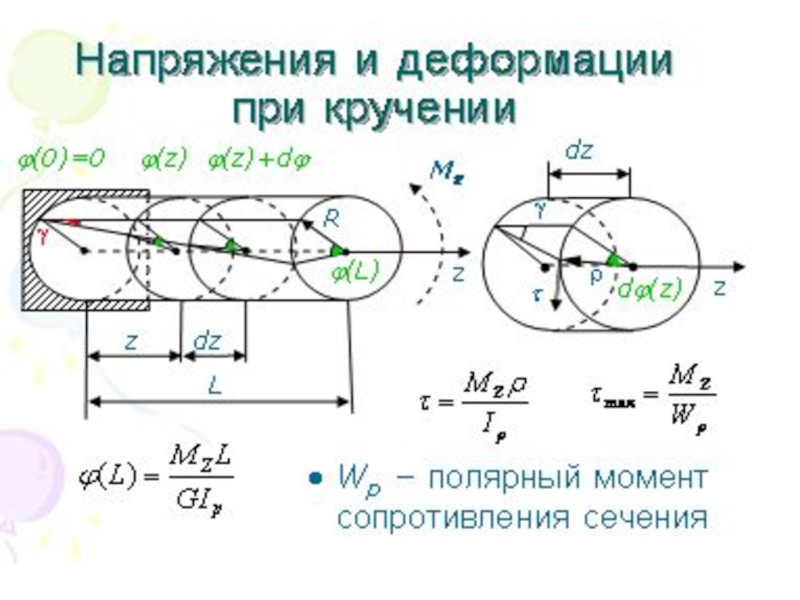
Слайд 137Напряжения и деформации при кручении
Wp – полярный момент сопротивления сечения
Mz
dz
z
ϕ(z)+dϕ
ϕ(z)
L
ϕ(L)
ϕ(0)=0
R
z
γ
τ
ρ
dz
dϕ(z)
z
γ
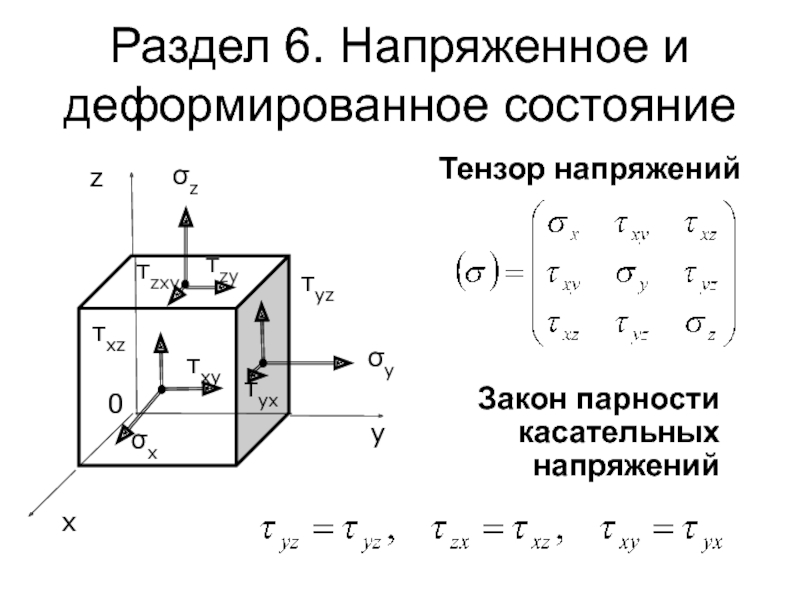
Слайд 138Раздел 6. Напряженное и деформированное состояние
Тензор напряжений
τxz
x
τxy
τyx
τyz
τzxy
τzy
σz
σy
σx
z
y
0
Закон парности касательных
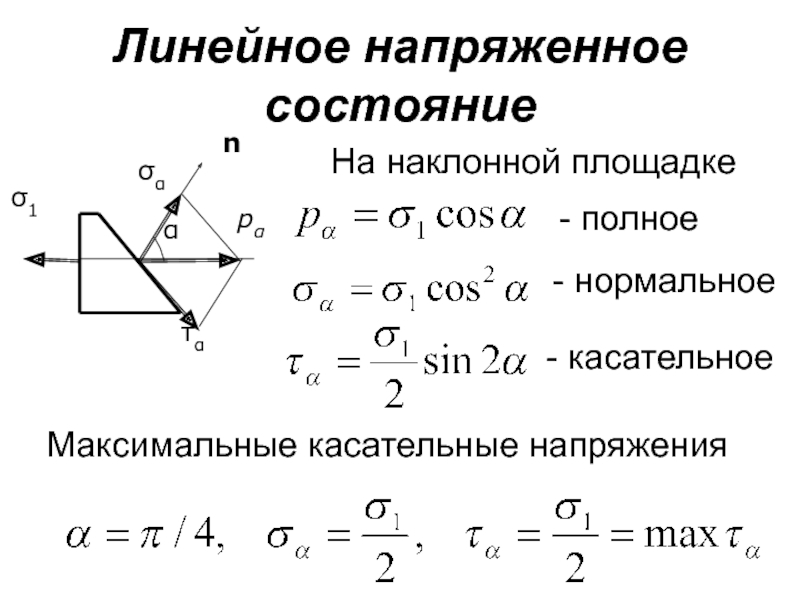
Слайд 139Линейное напряженное состояние
На наклонной площадке
pα
- полное
- нормальное
- касательное
Максимальные касательные напряжения
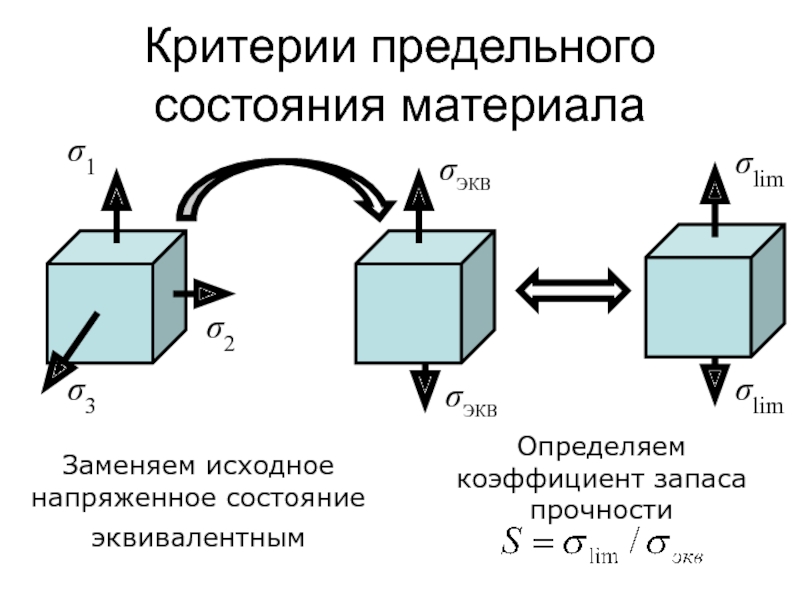
Слайд 143Критерии предельного состояния материала
σ2
σ3
σЭКВ
σЭКВ
σlim
σlim
Заменяем исходное напряженное состояние эквивалентным
Определяем коэффициент
σ1
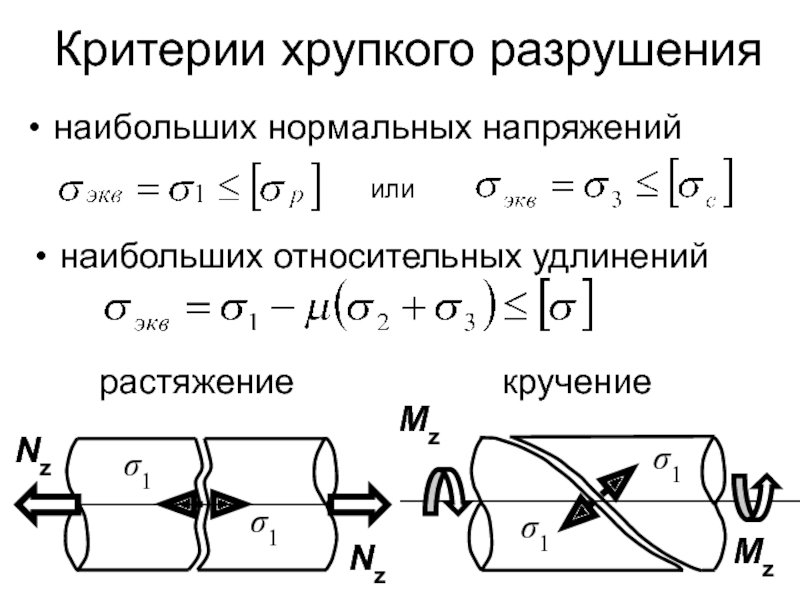
Слайд 144Критерии хрупкого разрушения
наибольших нормальных напряжений
или
наибольших относительных удлинений
растяжение
кручение
Nz
Nz
Mz
Mz
Слайд 145Критерии появления пластических деформаций
наибольших касательных напряжений
потенциальной энергии формоизменения
формулы
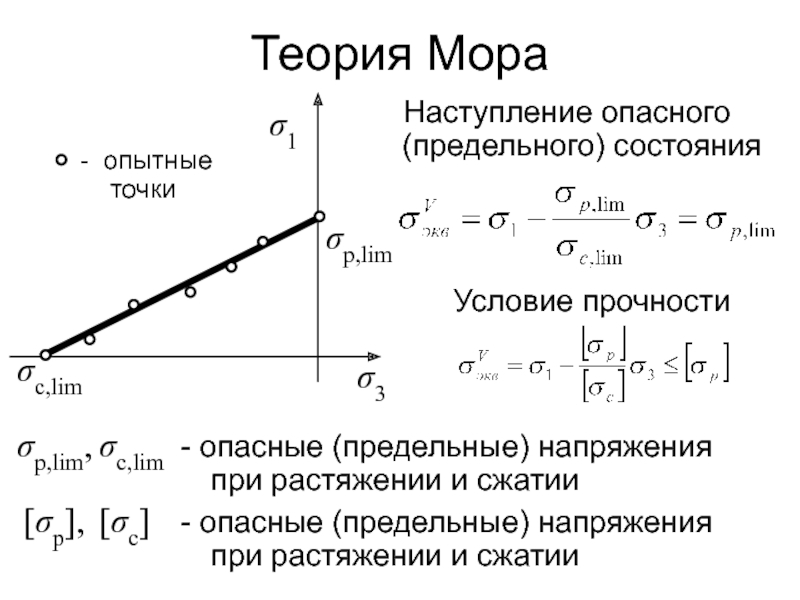
Слайд 146Теория Мора
- опытные точки
Наступление опасного (предельного) состояния
Условие прочности
σр,lim,
σс,lim
- опасные (предельные)
- опасные (предельные) напряжения при растяжении и сжатии
[σр],
[σc]
Слайд 148Геометрические характеристики плоских сечений
Площадь
Статические моменты
Координаты центра тяжести
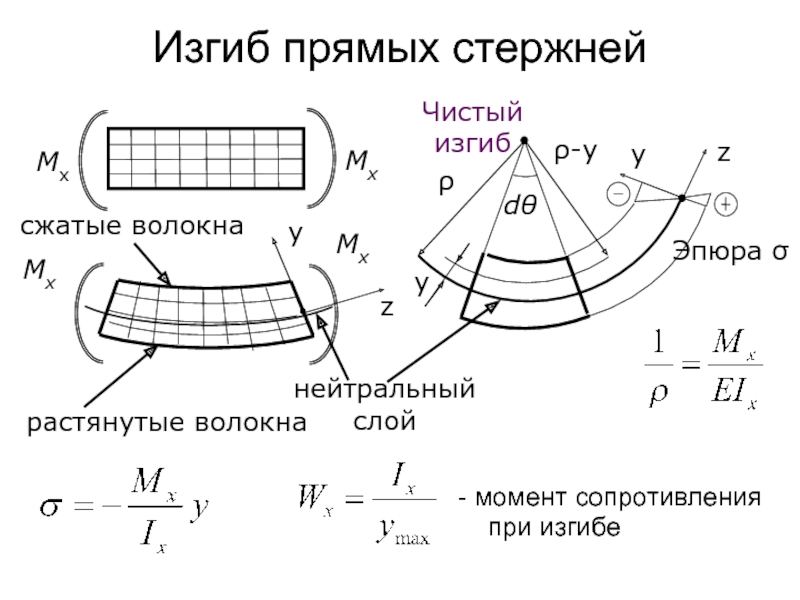
Слайд 153Изгиб прямых стержней
- момент сопротивления при изгибе
сжатые волокна
Чистый изгиб
z
растянутые волокна
нейтральный
Mx
Mx
Mx
Mx
y
Эпюра σ