- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 5: Волновая оптика. Оптика световых пучков. Оптические резонаторы презентация
Содержание
- 1. Лекция 5: Волновая оптика. Оптика световых пучков. Оптические резонаторы
- 2. Оптические пучки По законам волновой оптики любой
- 3. Гауссов пучок (излучение лазера) Решение волнового уравнения
- 4. Свойства Гауссова пучка Мощность Функция Гаусса
- 5. Свойства Гауссова пучка Глубина фокуса Для He-Ne
- 6. Прохождение Гауссова пучка через оптическую систему Для
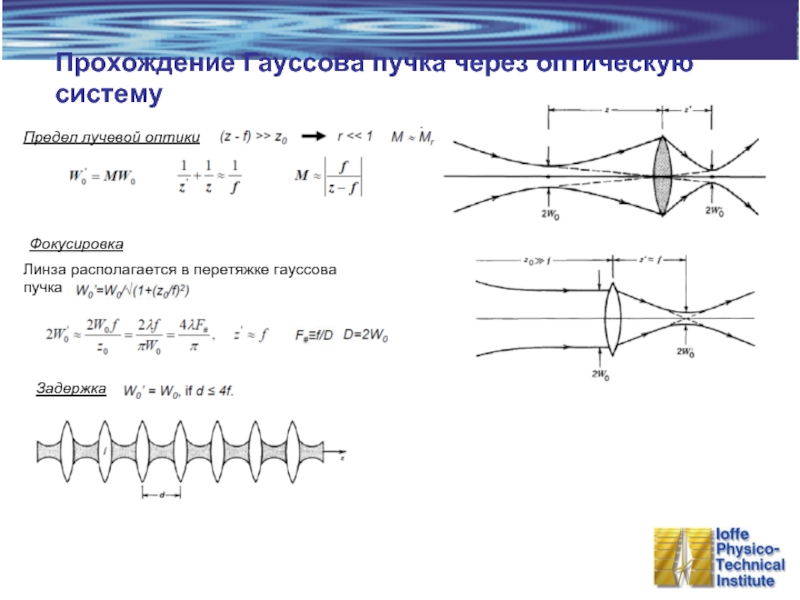
- 7. Прохождение Гауссова пучка через оптическую систему Фокусировка Задержка
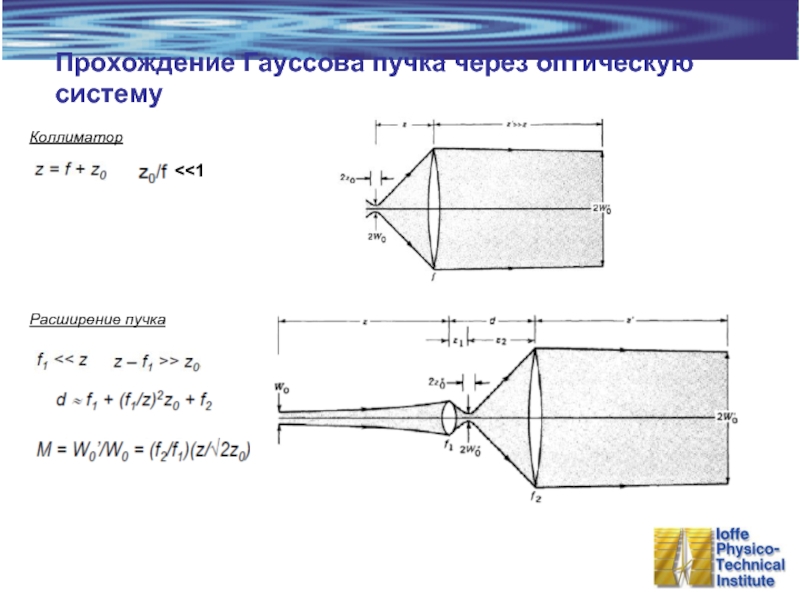
- 8. Прохождение Гауссова пучка через оптическую систему Коллиматор Расширение пучка
- 9. Другие решения уравнения Гельмгольца в параксиальном приближении
- 10. Оптические резонаторы Накапливают энергию на определенных резонансных
- 11. Эталон Фабри-Перо Два плоских зеркала на расстоянии
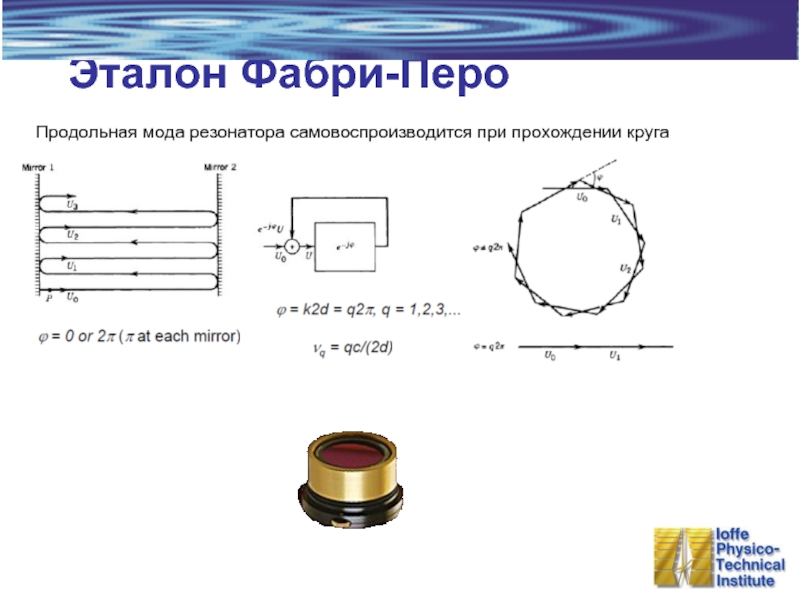
- 12. Эталон Фабри-Перо Продольная мода резонатора самовоспроизводится при прохождении круга
- 13. Эталон Фабри-Перо Потери и спектральная ширина
- 14. Эталон Фабри-Перо Потери и F Через приведенные
- 15. Резонатор как спектроанализатор
- 16. Резонатор Фабри-Перо со сферическими зеркалами Резонатор с
- 17. Продольные моды резонатора со сферическими зеркалами Резонатор
- 18. Гауссов пучок как фундаментальная поперечная мода резонатора
- 19. Поперечные моды резонатора со сферическими зеркалами Эрмитовы
Слайд 2Оптические пучки
По законам волновой оптики любой световой пучок расходится – дифракционная
Плоская волна – бесконечна в пространстве, но нет расходимости.
Сферическая волна – точечный источник и максимальная расходимость.
Параксиальное приближение – оптический пучок
Слайд 3Гауссов пучок
(излучение лазера)
Решение волнового уравнения Гельмгольца для монохроматической волны в параксиальном
Параметры A0= A1/jz0 и z0 определяются из граничных условий
Сферическая волна в параксиальном приближении дает параболическую волну, Гауссов пучок другое решение с квадратичной зависимость фазового фронта.
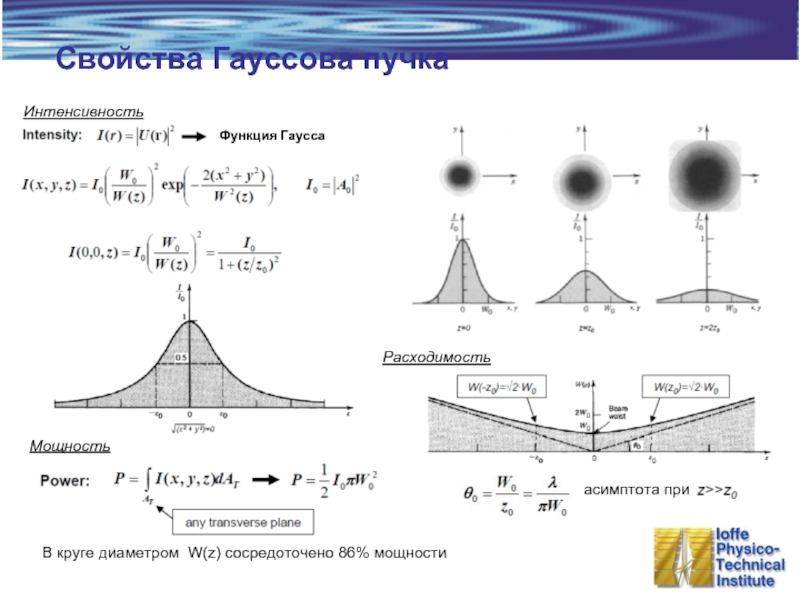
Слайд 4Свойства Гауссова пучка
Мощность
Функция Гаусса
Интенсивность
В круге диаметром W(z) сосредоточено 86% мощности
асимптота
Расходимость
Слайд 5Свойства Гауссова пучка
Глубина фокуса
Для He-Ne лазера (633 нм) размер пятна 2
плоская волна
Фаза и волновой фронт
искривление волнового фронта
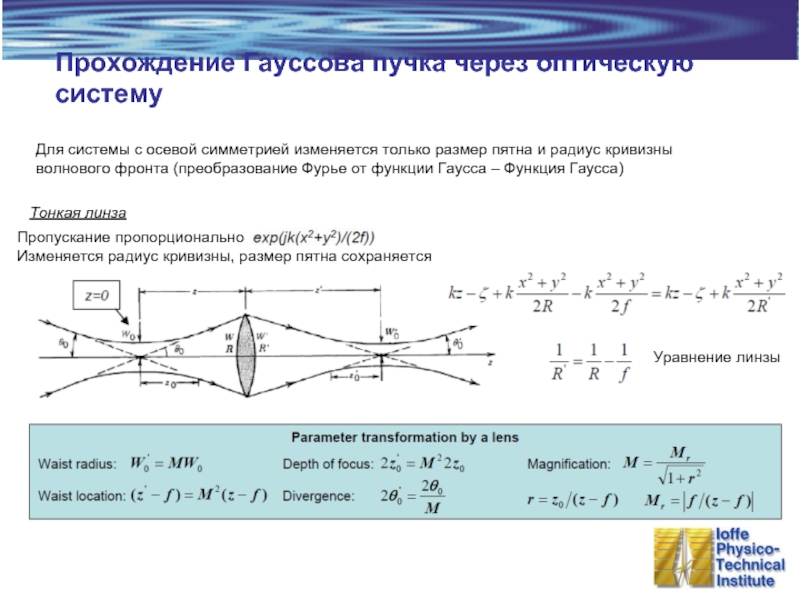
Слайд 6Прохождение Гауссова пучка через оптическую систему
Для системы с осевой симметрией изменяется
Уравнение линзы
Тонкая линза
Слайд 9Другие решения уравнения Гельмгольца в параксиальном приближении
Все функции имеют параболический
Слайд 10Оптические резонаторы
Накапливают энергию на определенных резонансных частотах (длинах волн)
Применение:
Лазеры
Волновая оптика пучков используется для анализа мод резонаторов
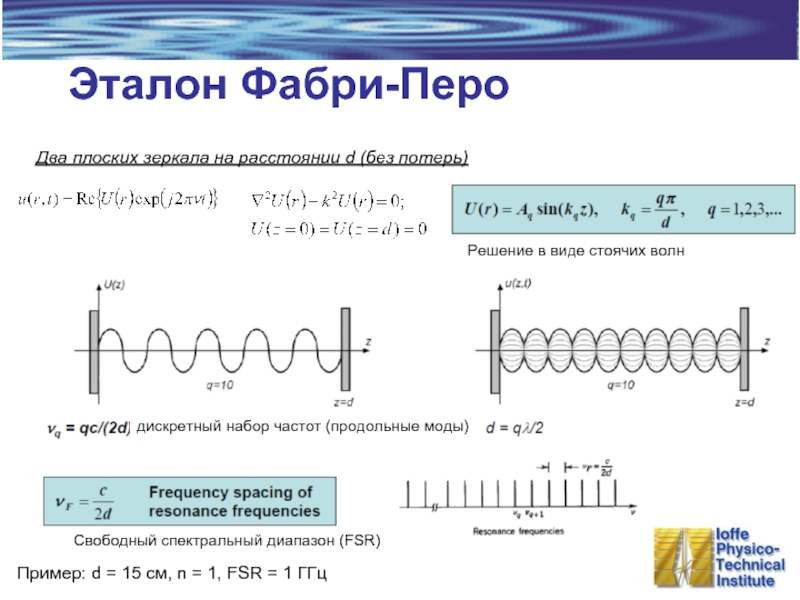
Слайд 11Эталон Фабри-Перо
Два плоских зеркала на расстоянии d (без потерь)
Пример: d
Решение в виде стоячих волн
Свободный спектральный диапазон (FSR)
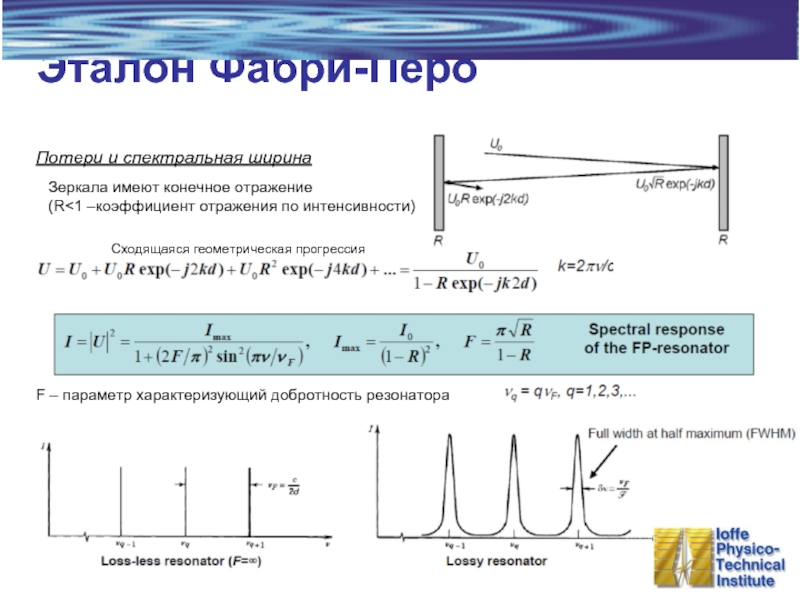
Слайд 13Эталон Фабри-Перо
Потери и спектральная ширина
F – параметр характеризующий добротность резонатора
Зеркала имеют конечное отражение
(R<1 –коэффициент отражения по интенсивности)
Сходящаяся геометрическая прогрессия
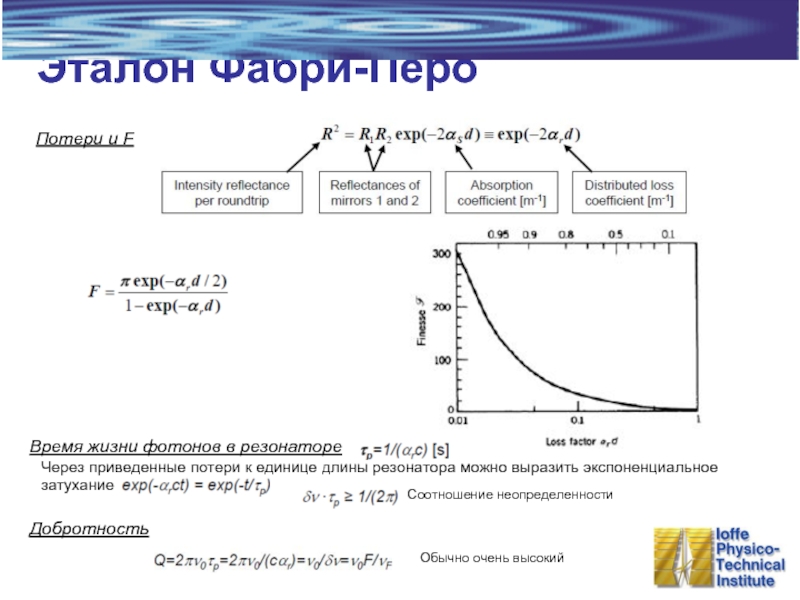
Слайд 14Эталон Фабри-Перо
Потери и F
Через приведенные потери к единице длины резонатора можно
Соотношение неопределенности
Добротность
Обычно очень высокий
Слайд 16Резонатор Фабри-Перо со сферическими зеркалами
Резонатор с плоскими зеркалами требует высокую точность
Для меридиальных лучей в приближении лучевой оптики
(пересекают оптическую ось)
Сферические зеркала более устойчивы к рассогласованию
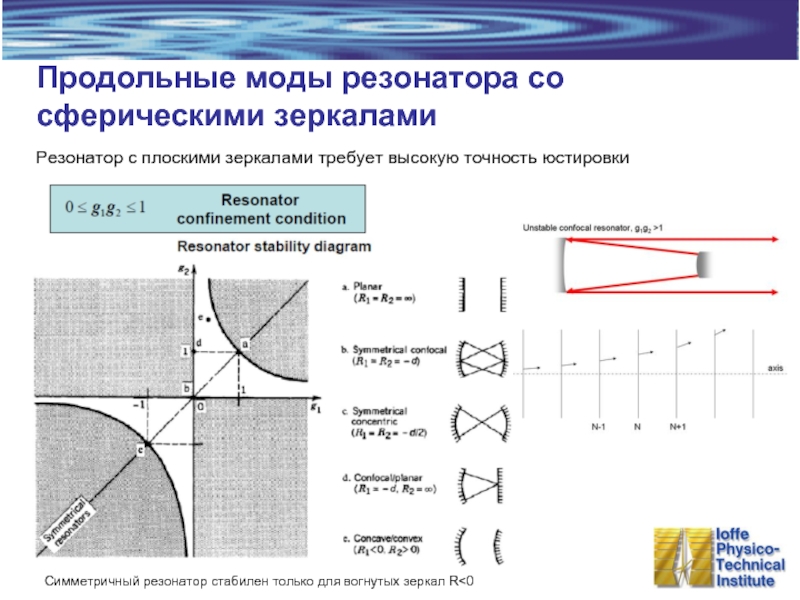
Слайд 17Продольные моды резонатора со сферическими зеркалами
Резонатор с плоскими зеркалами требует высокую
Симметричный резонатор стабилен только для вогнутых зеркал R<0
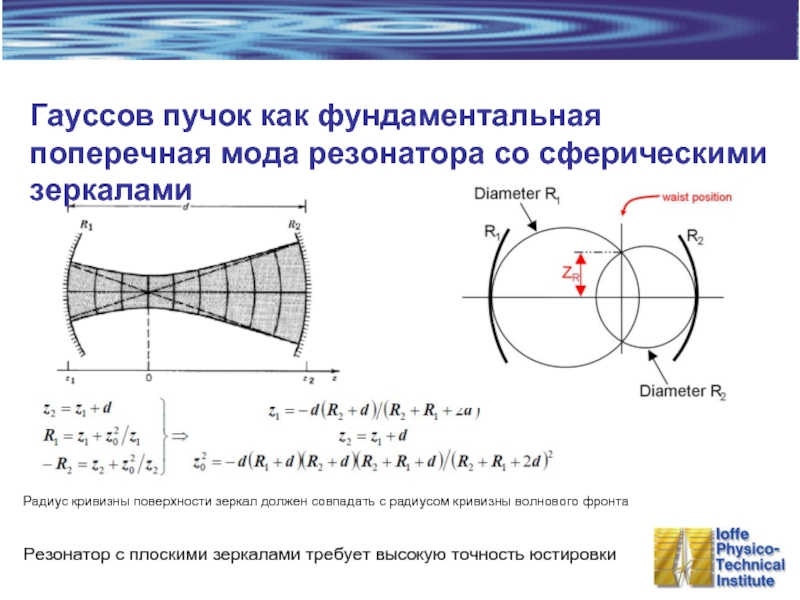
Слайд 18Гауссов пучок как фундаментальная поперечная мода резонатора со сферическими зеркалами
Резонатор с
Радиус кривизны поверхности зеркал должен совпадать с радиусом кривизны волнового фронта
Слайд 19Поперечные моды резонатора со сферическими зеркалами
Эрмитовы моды имеют тот же радиус
Однако при прохождении резонатора различные моды будут приобретать различный набег фазы.
Разным индексам будут соответствовать разные резонансные частоты