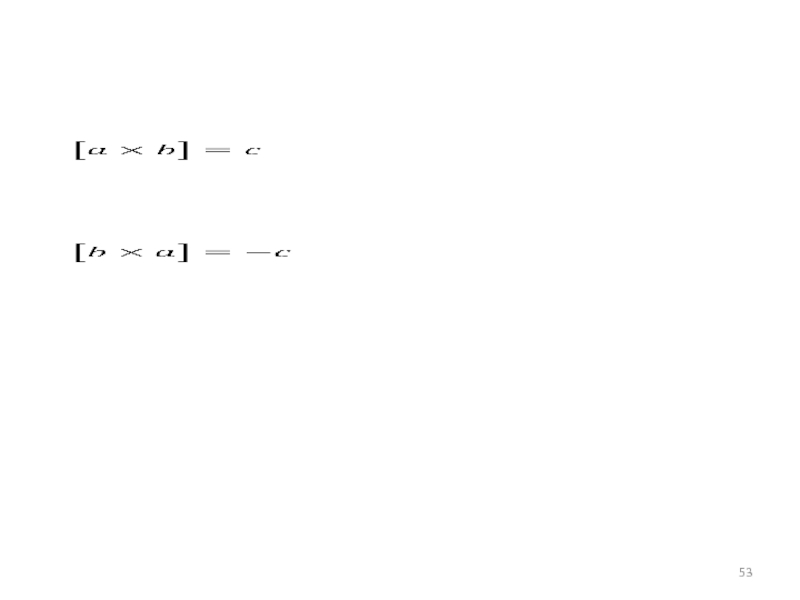- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 2АМ презентация
Содержание
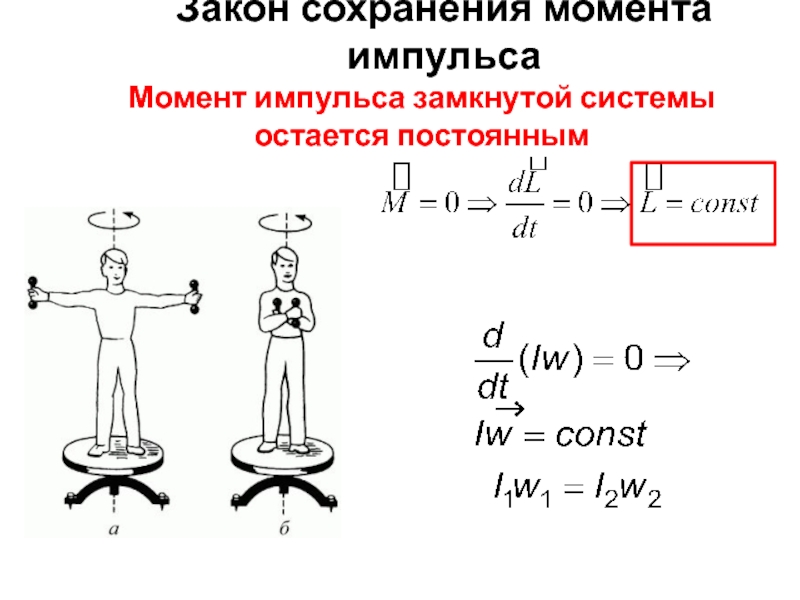
- 1. Лекция 2АМ
- 2. Лекция 2 1. Кинематика вращательного движения 2.
- 3. 1.Кинематика вращательного движения Поворот тела на
- 4. Мгновенная угловая скорость вращения
- 5. Связь между линейной и угловой скоростью
- 6. Векторное произведение 2-х векторов Результирующий вектор перпендикулярен плоскости в которой лежат перемножаемые вектора.
- 7. Равномерное вращение При равномерном вращении ω показывает,
- 8. Мгновенное угловое ускорение Изменение вектора
- 9. Движение по окружности с ускорением
- 10. Связь между линейным и угловым ускорениями Полное ускорение
- 11. Аналогии между линейными и угловыми характеристиками движения
- 12. Аналогии между законами прямолинейного движения и
- 13. 2.Поступательное движение твердого тела Система N материальных
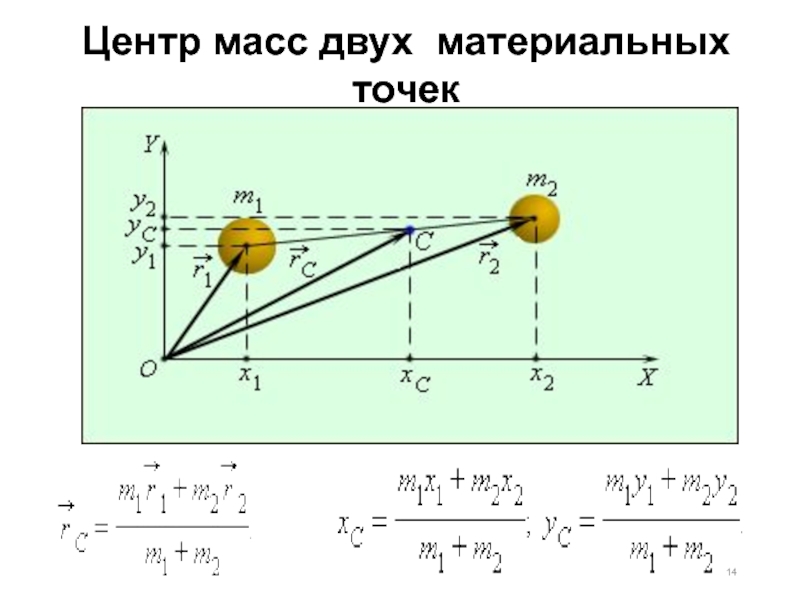
- 14. Центр масс двух материальных точек
- 15.
- 16. Импульс МТ, системы МТ и АбТвТ
- 17. Теорема о движении центра масс твердого тела
- 18. Моментом силы относительно т. О называется вектор, равный векторному произведению 3. Вращение твердого тела
- 19. Момент силы относительно неподвижной оси Проекция вектора
- 20. Момент импульса Момент импульса м.т. относительно неподвижной т.О
- 21. Вектор L направлен перпендикулярно плоскости, в которой
- 22. Основной закон динамики вращательного движения твердого тела
- 23. Момент импульса системы м.т. относительно центра т.О Основной закон динамики вращательного движения твердого тела
- 24. Момент инерции м.т., системы м.т., твердого тела
- 25. Свойства момента инерции Момент инерции в динамике
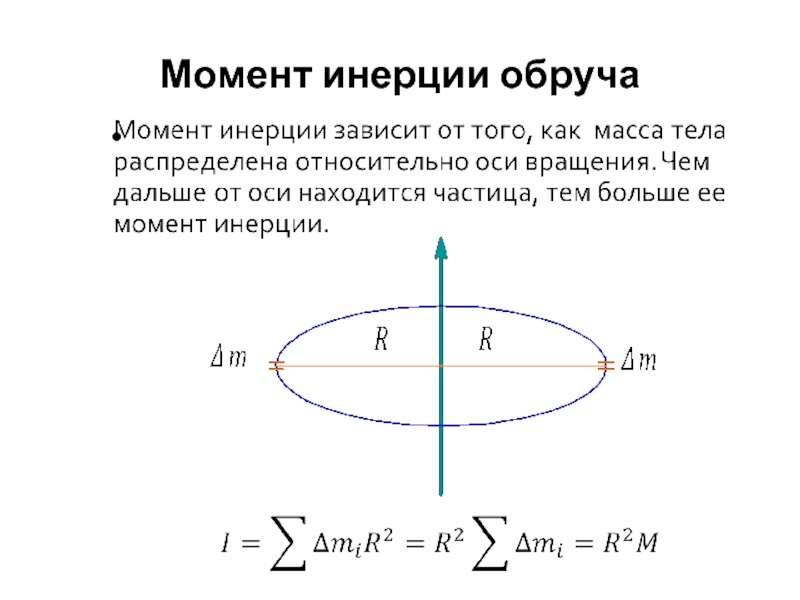
- 26. Момент инерции обруча
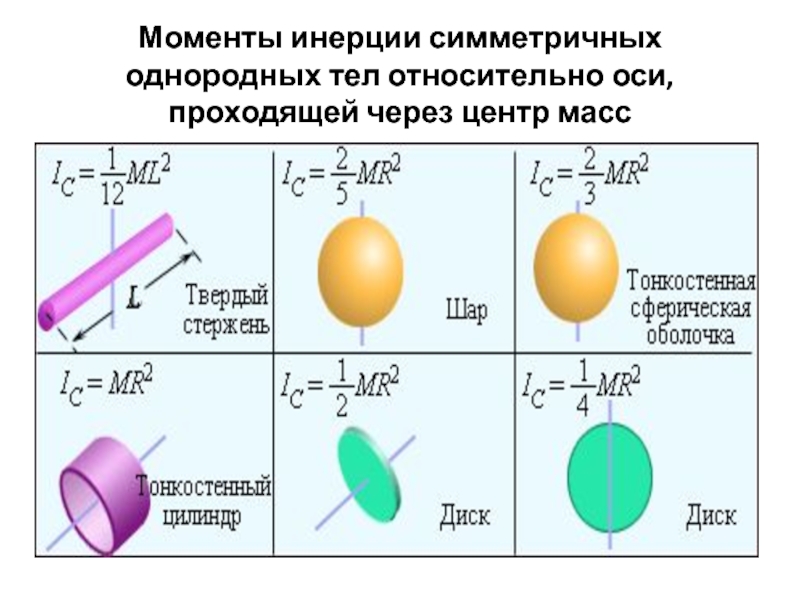
- 27. Моменты инерции симметричных однородных тел относительно оси, проходящей через центр масс
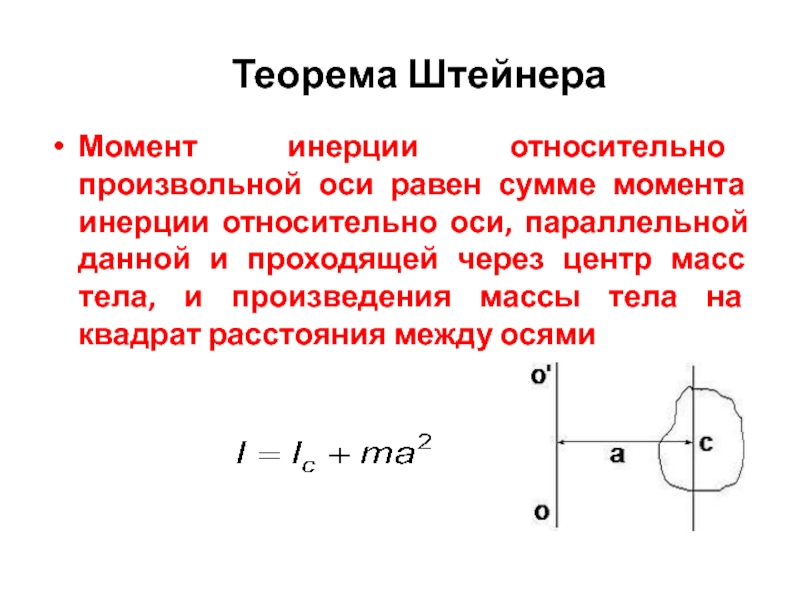
- 28. Теорема Штейнера Момент инерции относительно произвольной оси
- 29. 4.Работа и энергия Энергия- количественная мера движения
- 30. Работа Прямолинейное движение Криволинейное
- 31. Работа Прямолинейное движение Криволинейное
- 32. Работа Графически работа определяется по площади
- 33. Мощность Работа, совершаемая в единицу времени,
- 34. Теорема об изменении кинетической энергии Если действующая
- 35. Кинетическая энергия твердого тела Кинетическая энергия твердого
- 36. В общем случае кинетическая энергия твердого тела
- 37. Потенциальная энергия Если частица в каждой точке
- 38. 1 2
- 39. Неконсервативными (диссипативными) называются силы, работа которых зависит
- 40. Потенциальная энергия Каждой точке поля консервативных сил
- 41. Потенциальная энергия Работа консервативной силы равна убыли потенциальной энергии тела
- 42. Потенциальная энергия в поле тяжести Земли h
- 43. Величину Е, равную сумме потенциальной и кинетической
- 44. Закон сохранения механической энергии Изменение полной
- 45. Законы сохранения Система, для которой внешние силы
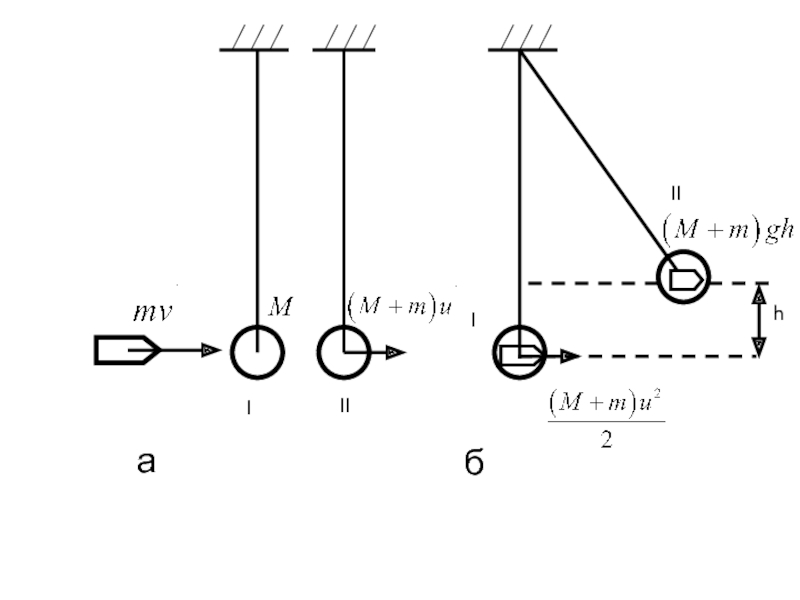
- 46. Пример использования законов сохранения импульса и механической энергии
- 47. а б I II II I h
- 48.
- 49. Закон сохранения момента импульса Момент импульса замкнутой системы остается постоянным
- 50. Закон сохранения момента импульса ?
- 51. Условия выполнения законов сохранения импульса, энергии и
- 52. 2. В незамкнутой системе: если проекция
- 53.
- 54. Теорема Эмми Нётер утверждает, что каждой непрерывной симметрии физической системы
- 55. Закон сохранения момента импульса – с изотропностью
- 56. Постулат 1. Принцип относительности «Движение системы
- 57. 1. Сокращение продольных размеров (при движении
- 58. Принцип эквивалентности (сильный): никакой эксперимент – ни
Лекция 2 1. Кинематика вращательного движения 2. Поступательное движение твердого тела. Теорема о движении центра масс 3. Вращение твердого тела. Основное уравнение динамики вращательного движения. 4. Работа и энергия. Законы сохранения
Слайд 2Лекция 2
1. Кинематика вращательного движения
2. Поступательное движение твердого тела. Теорема о
движении центра масс
3. Вращение твердого тела. Основное уравнение динамики вращательного движения.
4. Работа и энергия. Законы сохранения механической энергии, импульса, момента импульса.
3. Вращение твердого тела. Основное уравнение динамики вращательного движения.
4. Работа и энергия. Законы сохранения механической энергии, импульса, момента импульса.
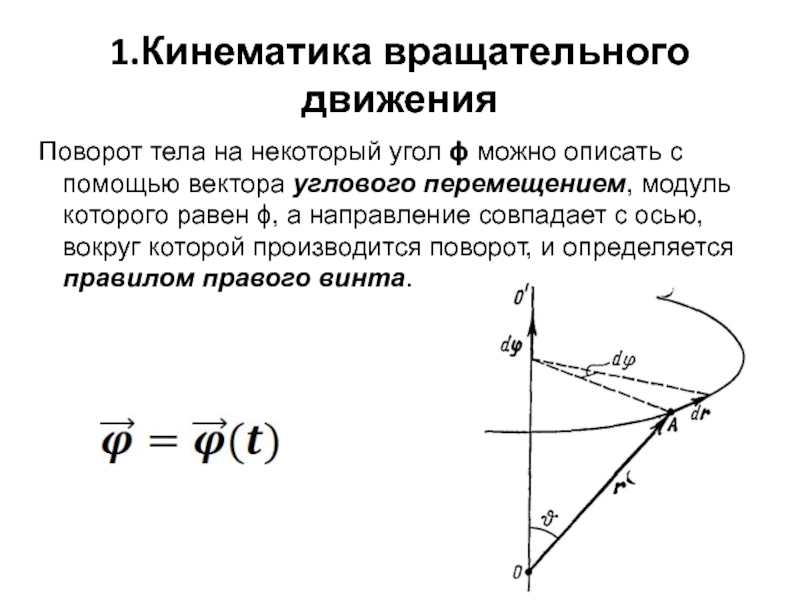
Слайд 31.Кинематика вращательного движения
Поворот тела на некоторый угол ϕ можно описать
с помощью вектора углового перемещением, модуль которого равен ϕ, а направление совпадает с осью, вокруг которой производится поворот, и определяется правилом правого винта.
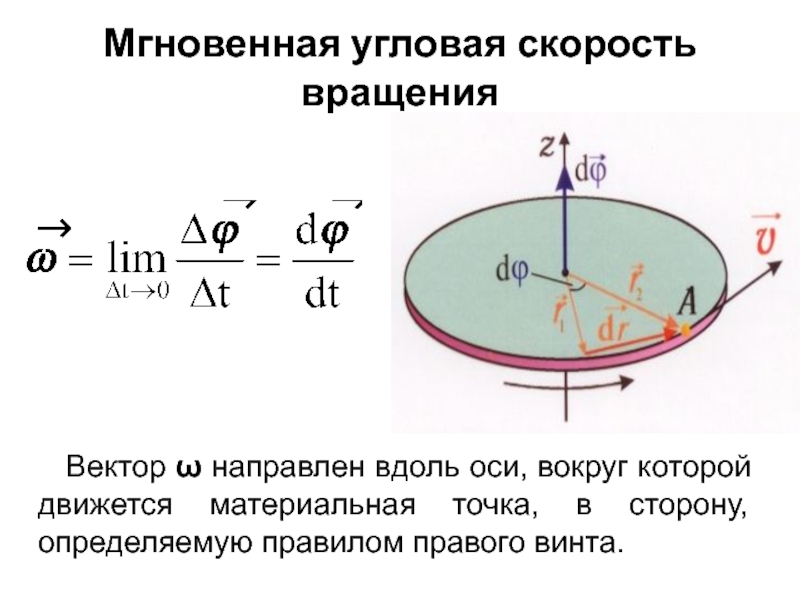
Слайд 4Мгновенная угловая скорость вращения
Вектор ω направлен вдоль оси,
вокруг которой движется материальная точка, в сторону, определяемую правилом правого винта.
Слайд 5
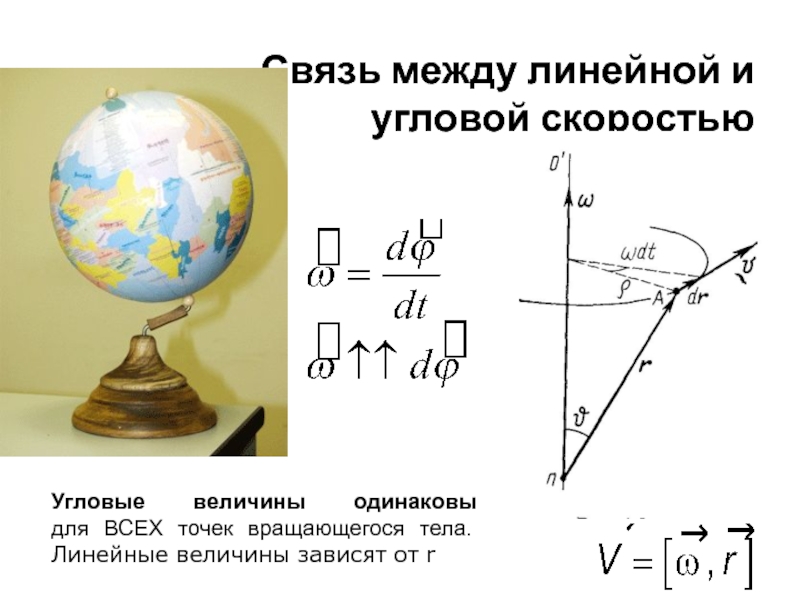
Связь между линейной и угловой скоростью
Угловые величины одинаковы
для ВСЕХ точек
вращающегося тела. Линейные величины зависят от r
Слайд 6
Векторное произведение 2-х векторов
Результирующий вектор перпендикулярен плоскости в которой лежат перемножаемые
вектора.
Слайд 7Равномерное вращение
При равномерном вращении ω показывает, на какой угол поворачивается тело
за единицу времени.
Период обращения Т - время, за которое тело делает один оборот, т.е. поворачивается на угол 2π. Поскольку промежутку времени Т соответствует угол поворота 2π, то
Период обращения Т - время, за которое тело делает один оборот, т.е. поворачивается на угол 2π. Поскольку промежутку времени Т соответствует угол поворота 2π, то
откуда период Т равен:
Число оборотов в единицу времени ν, равно:
Слайд 8Мгновенное угловое ускорение
Изменение вектора угловой скорости со временем характеризуют величиной,
называемой мгновенным угловым ускорением:
Направление вектора ε совпадает с направлением dω – приращения вектора ω.
[ε] = рад/с2
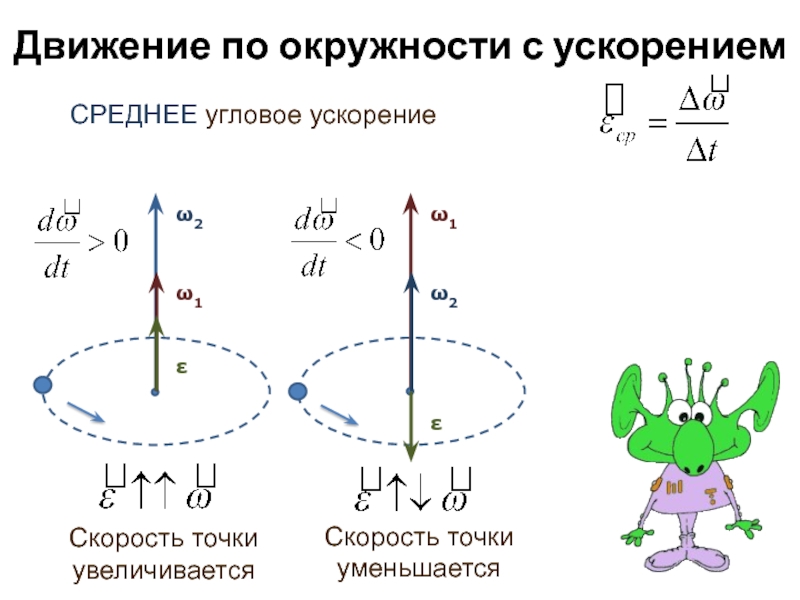
Слайд 9Движение по окружности с ускорением
СРЕДНЕЕ угловое ускорение
Скорость точки
увеличивается
Скорость точки
уменьшается
ω1
ω2
ε
ω2
ω1
ε
Слайд 11Аналогии между линейными и угловыми характеристиками движения
Физическая величина
Поступательное движение
Движение
по окружности
Связь
между характеристиками
Перемещение
Скорость
Ускорение
Угловое
Линейное
Угловая
Линейная
Угловое
Линейное
Слайд 12Аналогии между законами прямолинейного движения
и движения по окружности
Прямолинейное движение
Движение
по
окружности
Равномерное
Равнопеременное (равноускоренное)
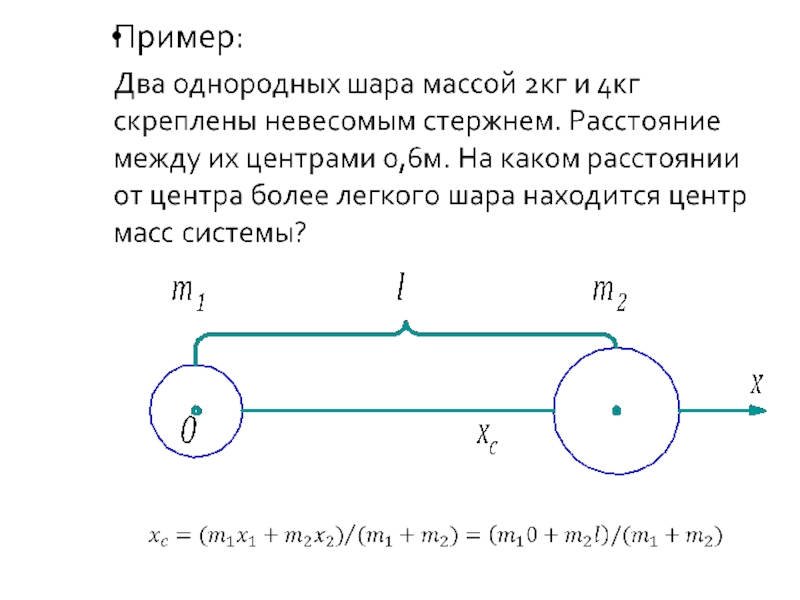
Слайд 132.Поступательное движение твердого тела
Система N материальных точек.
Центром инерции
( или центом масс) системы материальных точек называется точка С, положение которой задается радиус-вектором rC
Слайд 16Импульс МТ, системы МТ и АбТвТ
1)
2)
3)
Суммарный импульс системы МТ или
твердого тела равен произведению массы системы на скорость центра масс.
Слайд 17Теорема о движении центра масс твердого тела
Центр масс твердого тела движется
так, как двигалась бы материальная точка с массой, равной массе тела, под действием всех внешних сил, приложенных к телу.
Если , то центр масс движется прямолинейно и равномерно, либо покоится.
Если , то центр масс движется прямолинейно и равномерно, либо покоится.
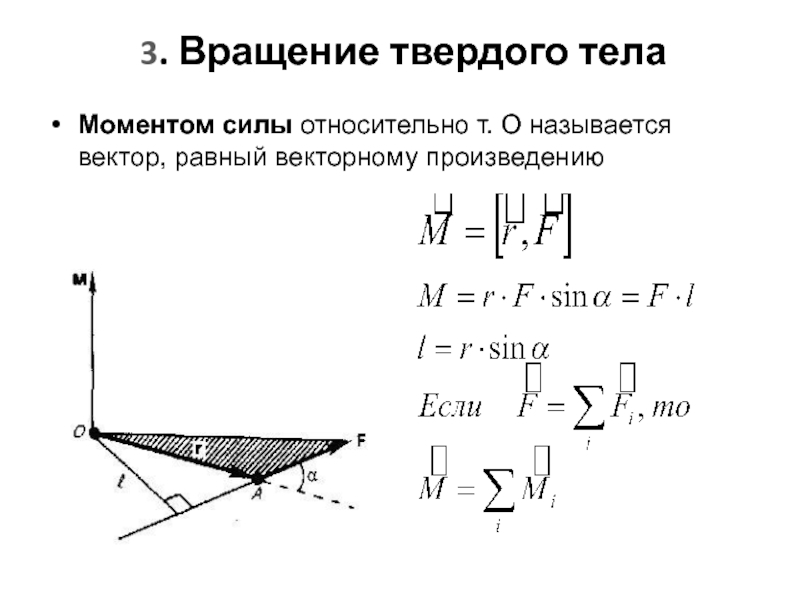
Слайд 18Моментом силы относительно т. О называется вектор, равный векторному произведению
3.
Вращение твердого тела
Слайд 19Момент силы относительно неподвижной оси
Проекция вектора M на некоторую ось z,
проходящую через точку О , относительно которой определен момент силы,
называется моментом силы
относительно этой оси
Мz = [r,F]z
Мz = [r,F]z
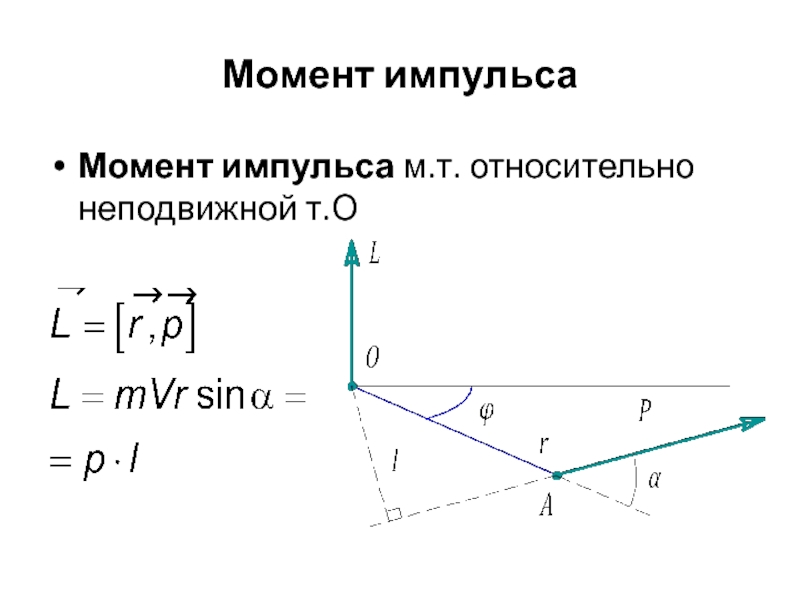
Слайд 21Вектор L направлен перпендикулярно плоскости, в которой лежат сила и точка
О, так что вращение, обусловленное силой, и направление вектора L образуют правовинтовую систему.
m
O
Слайд 22Основной закон динамики вращательного движения твердого тела
Для тела, вращающегося относительно оси
Z момент импульса равен
Слайд 23Момент импульса системы м.т. относительно центра т.О
Основной закон динамики вращательного движения
твердого тела
Слайд 24Момент инерции м.т., системы м.т., твердого тела
Момент инерции – динамический параметр
при вращательном движении
Момент инерции м.т.
Момент инерции системы м.т.
Момент инерции
твердого тела
Момент инерции м.т.
Момент инерции системы м.т.
Момент инерции
твердого тела
mi
Z
Слайд 25Свойства момента инерции
Момент инерции в динамике вращательного движения играет ту же
роль, что и масса тела в динамике поступательного движения.
Масса – внутреннее свойство данного тела, не зависящее от его движения.
Момент инерции тела зависит от того, вокруг какой оси оно вращается.
Для разных осей вращения моменты инерции одного и того же тела различны.
Масса – внутреннее свойство данного тела, не зависящее от его движения.
Момент инерции тела зависит от того, вокруг какой оси оно вращается.
Для разных осей вращения моменты инерции одного и того же тела различны.
Слайд 28Теорема Штейнера
Момент инерции относительно произвольной оси равен сумме момента инерции относительно
оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями
Слайд 294.Работа и энергия
Энергия- количественная мера движения и взаимодействия всех видов материи.
Соответственно различают механическую, внутреннюю, электромагнитную, ядерную и пр. энергию.
Механическая энергия складывается из кинетической и потенциальной.
Кинетическая энергия- энергия движения, определяется скоростями и массами движущихся тел.
Потенциальная энергия – энергия положения, определяется взаимным расположением взаимодействующих тел.
Механическая энергия складывается из кинетической и потенциальной.
Кинетическая энергия- энергия движения, определяется скоростями и массами движущихся тел.
Потенциальная энергия – энергия положения, определяется взаимным расположением взаимодействующих тел.
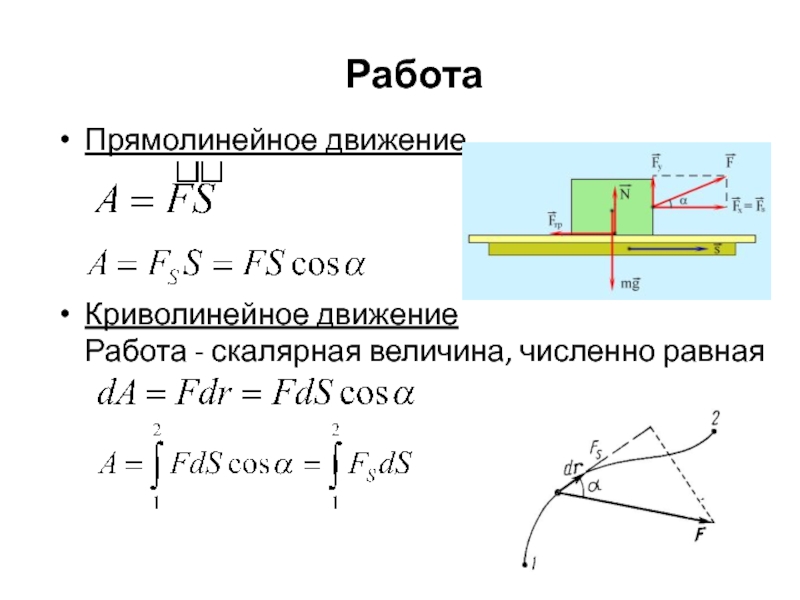
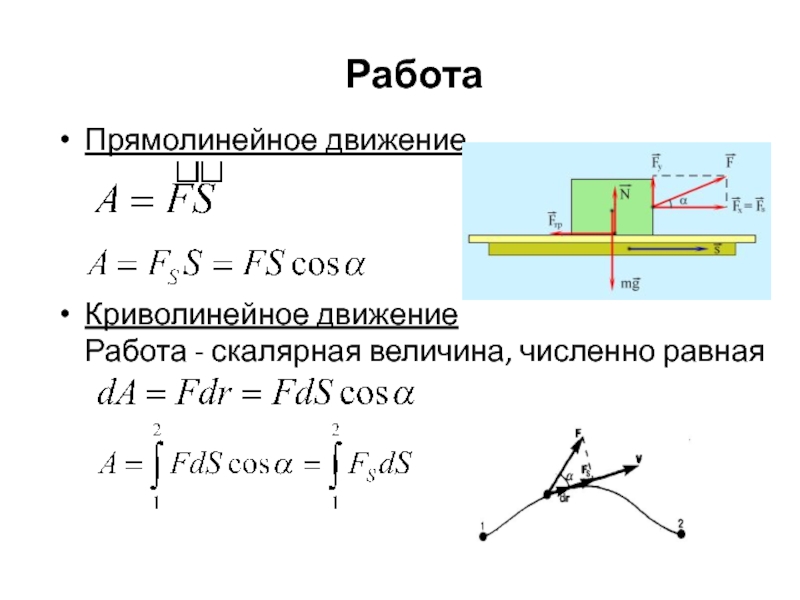
Слайд 30Работа
Прямолинейное движение
Криволинейное движение
Работа - скалярная величина, численно равная
Слайд 31Работа
Прямолинейное движение
Криволинейное движение
Работа - скалярная величина, численно равная
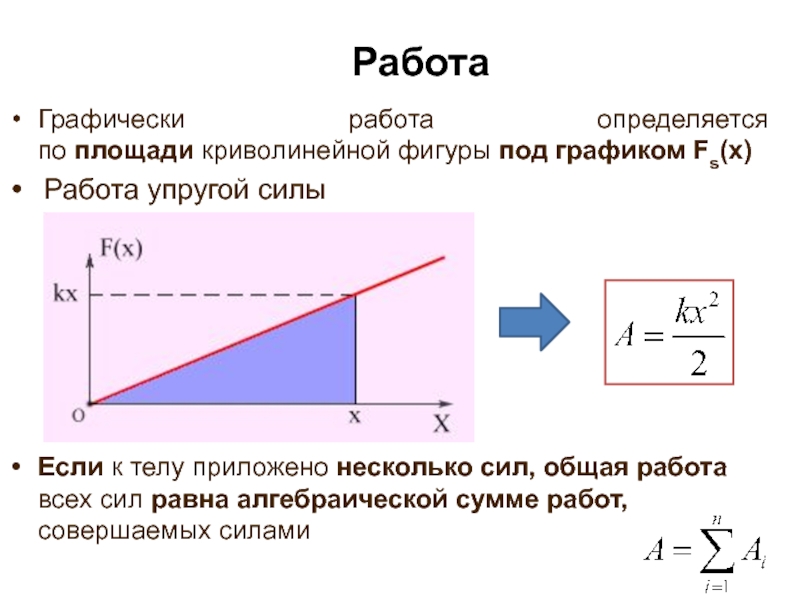
Слайд 32Работа
Графически работа определяется
по площади криволинейной фигуры под графиком Fs(x)
Работа
упругой силы
Если к телу приложено несколько сил, общая работа всех сил равна алгебраической сумме работ, совершаемых силами
Если к телу приложено несколько сил, общая работа всех сил равна алгебраической сумме работ, совершаемых силами
Слайд 33Мощность
Работа, совершаемая в единицу времени, называется мощностью.
Единицы измерения: [A] –
Джоуль
[P] – Ватт ,
внесистемные ед.: [л.с] – 736 Вт
[P] – Ватт ,
внесистемные ед.: [л.с] – 736 Вт
Слайд 34Теорема об изменении кинетической энергии
Если действующая на частицу сила F отлична
от нуля , то Ек изменяется, и ее приращение определяется работой силы F.
Кинетическая энергия системы м.т.
Изменение кинетической энергии системы тел равно работе всех сил, действующих на систему.
Кинетическая энергия системы м.т.
Изменение кинетической энергии системы тел равно работе всех сил, действующих на систему.
Слайд 35Кинетическая энергия твердого тела
Кинетическая энергия твердого тела, движущегося поступательно
Кинетическая энергия простого
вращательного движения (вокруг неподвижной оси с угловой скоростью w)
Слайд 36В общем случае кинетическая энергия твердого тела складывается из энергии поступательного
движения со скоростью, равной скорости движения центра масс, и энергии вращения вокруг оси, проходящей через центр масс тела.
Кинетическая энергия при плоском движении
Слайд 37Потенциальная энергия
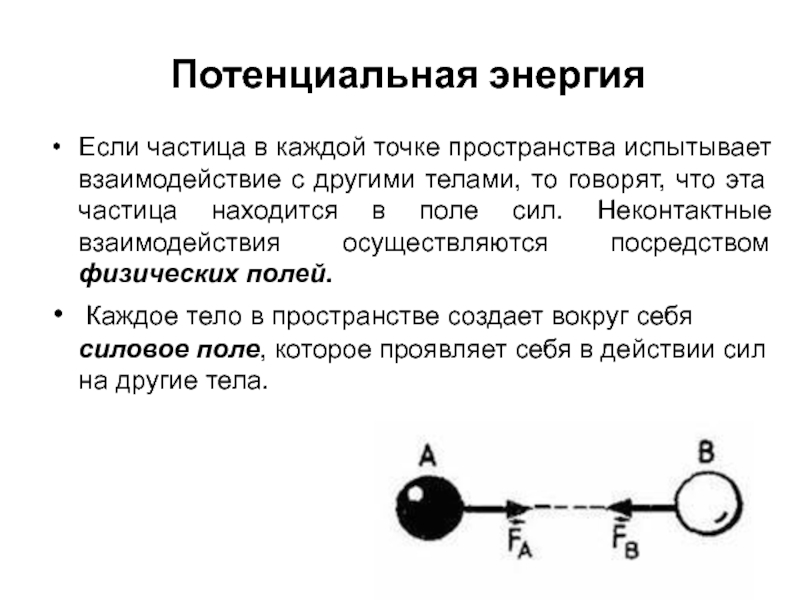
Если частица в каждой точке пространства испытывает взаимодействие с другими
телами, то говорят, что эта частица находится в поле сил. Неконтактные взаимодействия осуществляются посредством физических полей.
Каждое тело в пространстве создает вокруг себя силовое поле, которое проявляет себя в действии сил на другие тела.
Каждое тело в пространстве создает вокруг себя силовое поле, которое проявляет себя в действии сил на другие тела.
Слайд 38
1
2
А1
А2
А3
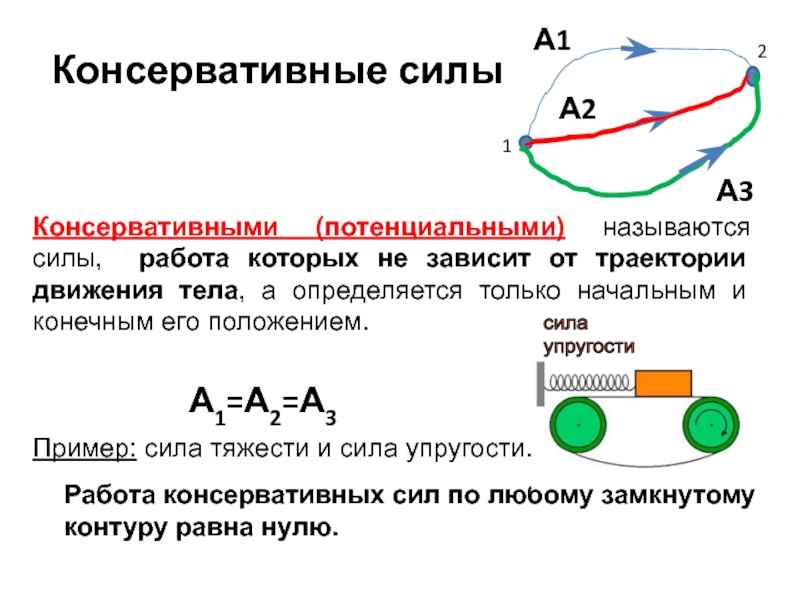
А1=А2=А3
Работа консервативных сил по любому замкнутому контуру равна нулю.
Консервативные силы
Консервативными (потенциальными)
называются силы, работа которых не зависит от траектории движения тела, а определяется только начальным и конечным его положением.
Пример: сила тяжести и сила упругости.
Пример: сила тяжести и сила упругости.
Слайд 39Неконсервативными (диссипативными) называются силы, работа которых зависит от формы траектории и
пройденного пути.
Пример: сила трения скольжения, силы сопротивления воздуха или жидкости.
Пример: сила трения скольжения, силы сопротивления воздуха или жидкости.
Неконсервативные силы
сила
трения
Слайд 40Потенциальная энергия
Каждой точке поля консервативных сил можно сопоставить некоторую функцию координат
Еп( r ), которая определяет потенциальную энергию частицы в этом поле.
1
2
0
Потенциальная энергия определена с точностью до произвольной постоянной .
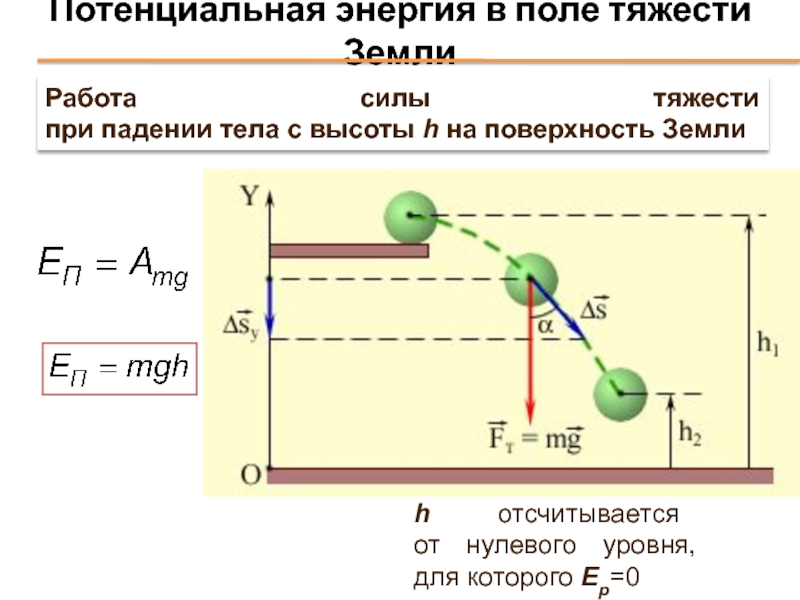
Слайд 42Потенциальная энергия в поле тяжести Земли
h отсчитывается
от нулевого уровня,
для которого
Ер=0
Работа силы тяжести
при падении тела с высоты h на поверхность Земли
Слайд 43Величину Е, равную сумме потенциальной и кинетической энергии, называют полной механической
энергией
Из (1-3) получим:
Изменение полной механической энергии
Слайд 44Закон сохранения механической энергии
Изменение полной механической энергии системы частиц равно работе
диссипативных сил, действующих на систему
Если на систему частиц действует только консервативные силы, то полная механическая энергия системы частиц сохраняется:
.
Слайд 45Законы сохранения
Система, для которой внешние силы отсутствуют, называют замкнутой (изолированной).
Для замкнутых
систем выполняются законы сохранения:
Энергии
Импульса
Момента импульса
Эти законы тесно связаны со свойствами пространства и времени.
Законы сохранения являются фундаментальными законами природы
Энергии
Импульса
Момента импульса
Эти законы тесно связаны со свойствами пространства и времени.
Законы сохранения являются фундаментальными законами природы
Слайд 51Условия выполнения законов сохранения импульса, энергии и момента импульса
1. В замкнутой
системе материальных точек сохраняются импульс, момент импульса и энергия (для упругого соударения – механическая энергия, для неупругого соударения – полная энергия)
Слайд 522. В незамкнутой системе:
если проекция суммы внешних сил на некоторую
ось равна нулю, то проекция импульса системы на эту ось будет оставаться постоянной;
если проекция моментов внешних сил на некоторую ось равна нулю, то проекция момента импульса системы на эту ось будет оставаться постоянной;
если работа внешних сил равна нулю, то полная энергия системы будет оставаться постоянной.
если проекция моментов внешних сил на некоторую ось равна нулю, то проекция момента импульса системы на эту ось будет оставаться постоянной;
если работа внешних сил равна нулю, то полная энергия системы будет оставаться постоянной.
Слайд 54Теорема Эмми Нётер утверждает, что каждой непрерывной симметрии физической системы соответствует некоторый закон сохранения.
Закон сохранения
импульса – с однородностью пространства (однородность означает отсутствие предпочтений при выборе точки пространства: все точки равноправны);
Слайд 55Закон сохранения момента импульса – с изотропностью пространства (изотропность означает отсутствие
предпочтения в выборе направления в пространстве: все направления одинаковы);
Закон сохранения энергии – с однородностью времени (все явления природы проходят одинаково, несмотря на выбор периода времени, когда это явление происходит или рассматривается).
Закон сохранения энергии – с однородностью времени (все явления природы проходят одинаково, несмотря на выбор периода времени, когда это явление происходит или рассматривается).
Слайд 56Постулат 1. Принцип относительности
«Движение системы отсчёта по инерции не может
быть обнаружено никакими физическими опытами внутри закрытой лаборатории, связанной с этой системой отсчёта»
Постулат 2. Принцип постоянства скорости света
«Свет в пустоте всегда распространяется
с определенной скоростью с, не зависящей
от движения излучающего тела»
Постулат 2. Принцип постоянства скорости света
«Свет в пустоте всегда распространяется
с определенной скоростью с, не зависящей
от движения излучающего тела»
Постулаты специальной теории относительности Эйнштейна (1905 г.).
Слайд 571. Сокращение продольных размеров
(при движении с околосветовой скоростью)
2. Замедление времени
(при движении с околосветовой скоростью)
3. Запрет скоростей, больших скорости света
4. Увеличение массы
(при движении с околосветовой скоростью)
Основные выводы из специальной
теории относительности Эйнштейна (1905 г.)
Слайд 58Принцип эквивалентности (сильный): никакой эксперимент – ни механический, ни какой-либо другой
– не дает возможности отличить инертную массу от гравитационной
