- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Haemodynamics Haemorheology презентация
Содержание
- 1. Haemodynamics Haemorheology
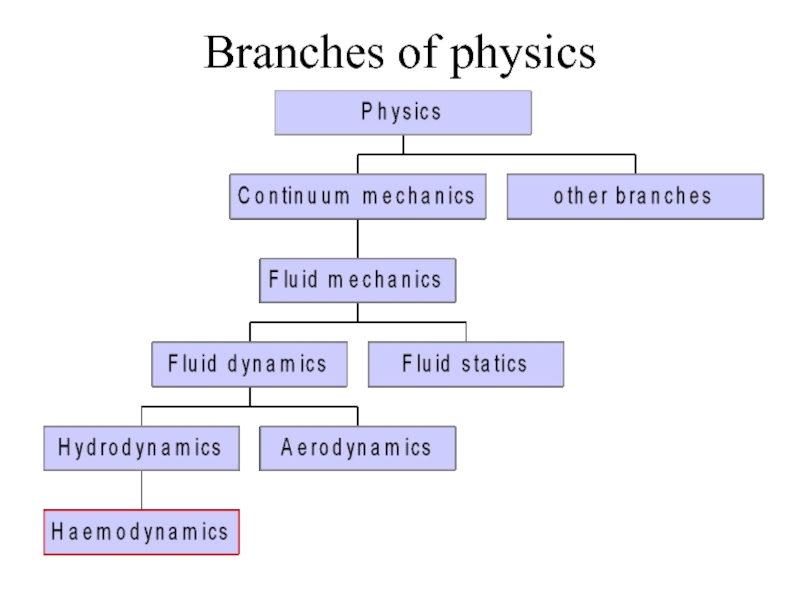
- 2. Branches of physics
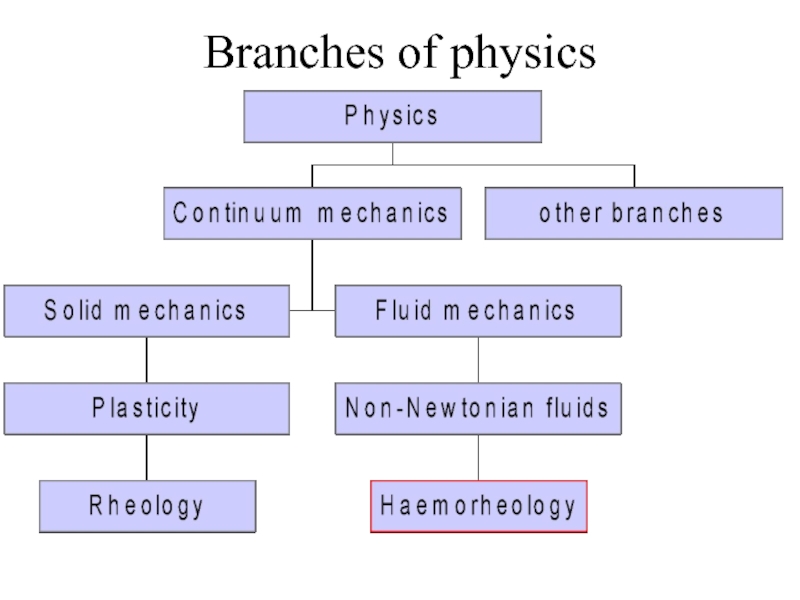
- 3. Branches of physics
- 4. Laminar and turbulent flow (a) occurs when
- 5. Viscosity The viscosity of a fluid is
- 6. Viscosity Viscosity is a property of the
- 7. Newton's Law of Viscosity F is the
- 8. Newtonian fluid fluid in which the viscous
- 9. Reynolds number Is the important dimensionless quantity
- 10. Reynolds number Used to help predict
- 11. Reynolds number wherein: vs - mean
- 12. Pascal's law Pascal's law is a principle
- 13. Bernoulli's principle ρv2/2 + ρgh + p
- 14. Hagen–Poiseuille law flow of liquid depends
- 15. Hagen–Poiseuille law The Pressure Gradient (∆P) :
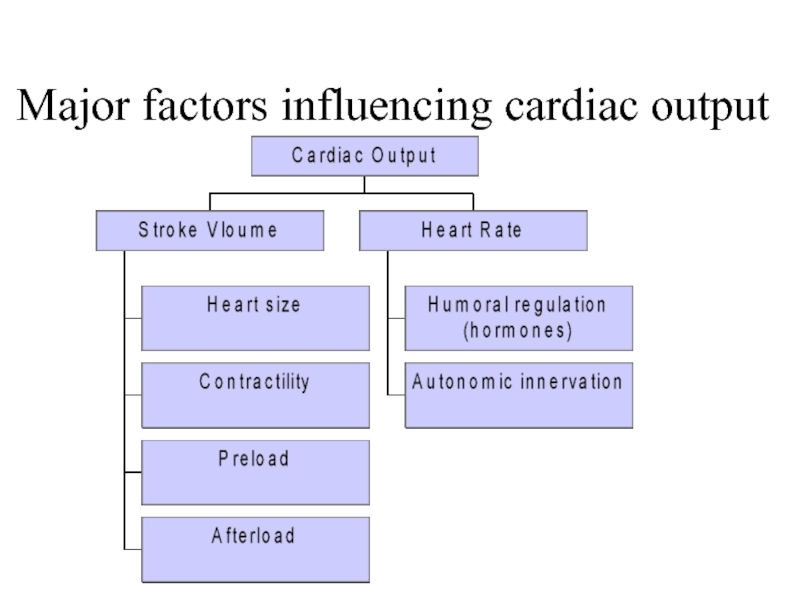
- 16. Cardiac output Is the volume of
- 17. Major factors influencing cardiac output
- 18. Frank–Starling law The Frank–Starling law of the
- 19. Myocardial contractility This results in better
- 20. Preload Preload is the end diastolic volume
- 21. Afterload Afterload is the stress in the
- 22. Vascular resistance Vascular resistance is the resistance
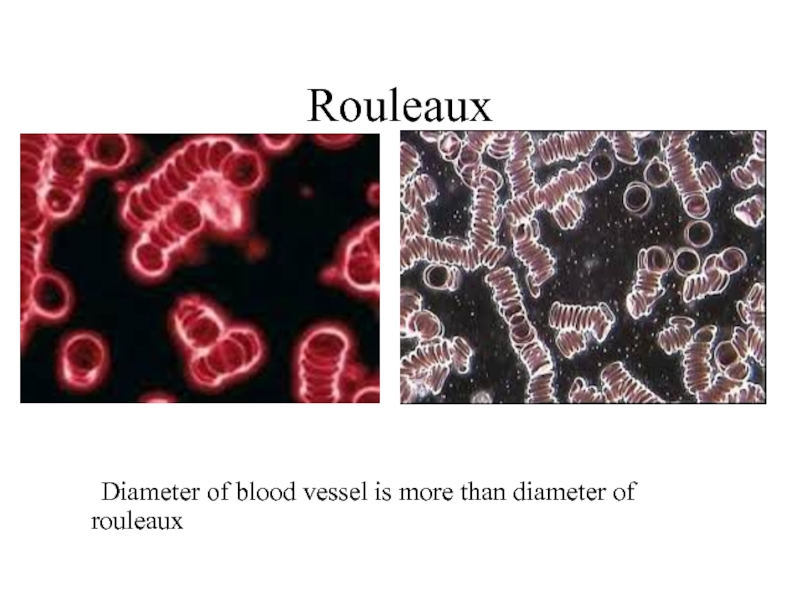
- 23. Rouleaux Rouleaux are stacks or aggregations of
- 24. Rouleaux Diameter of blood vessel is more than diameter of rouleaux
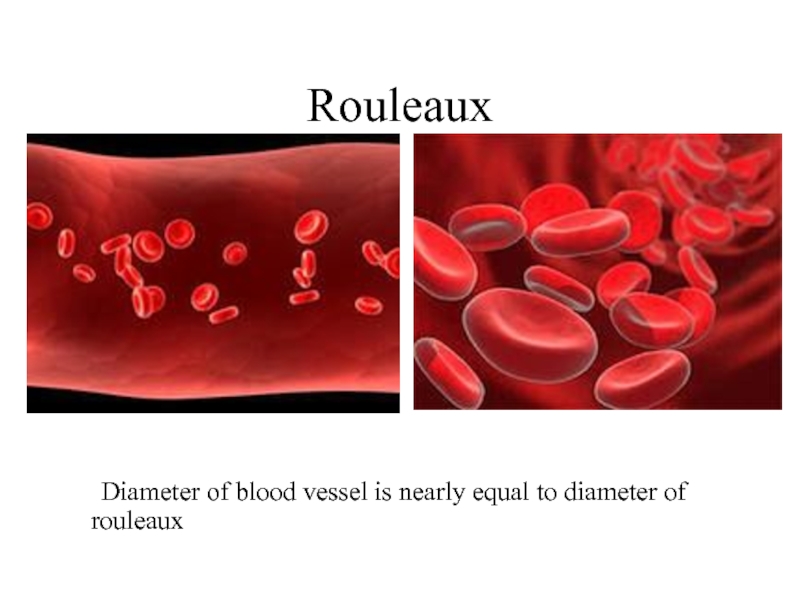
- 25. Rouleaux Diameter of blood vessel is nearly equal to diameter of rouleaux
- 26. Rouleaux Diameter of blood vessel is less than diameter of RBC
- 27. Hagen–Poiseuille law Pressure gradient: created by the
- 28. Now summarize three major concepts presented in this lecture 1. 2. 3.
Слайд 4Laminar and turbulent flow
(a) occurs when a fluid flows in parallel
(b) is a flow regime that demonstrates chaotic changes in pressure and flow velocity
Слайд 5Viscosity
The viscosity of a fluid is a measure of its resistance
Слайд 6Viscosity
Viscosity is a property of the fluid which opposes the relative
Слайд 7Newton's Law of Viscosity
F is the shear stress in the fluid
η
dV/dZ is the derivative of the velocity component that is parallel to the direction of shear, relative to displacement in the perpendicular direction.
S is the surface (area) between fluid and the tube.
Слайд 8Newtonian fluid
fluid in which the viscous stresses arising from its flow,
Non-Newtonian fluid
viscosity is dependent on shear rate or shear rate history.
Shear thickening (dilatant) - apparent viscosity increases with increased stress.
Shear thinning (pseudoplastic) - apparent viscosity decreases with increased stress
Слайд 9Reynolds number
Is the important dimensionless quantity refers to ratio of inertial
Слайд 10Reynolds number
Used to help predict flow patterns in different fluid
At low Reynolds numbers viscous forces are dominant, and is characterized by smooth, constant fluid motion (laminar flow).
At high Reynolds numbers flow is dominated by inertial forces, which tend to produce chaotic eddies, vortices and other flow instabilities (turbulent flow).
Слайд 11Reynolds number
wherein:
vs - mean fluid velocity, [m/s]
L - characteristic
μ - (absolute) dynamic fluid viscosity, [Pa*s]
ν - kinematic fluid viscosity: ν = μ / ρ, [m²/s]
ρ - fluid density, [kg*m-3]
Слайд 12Pascal's law
Pascal's law is a principle in fluid mechanics that states
Слайд 13Bernoulli's principle
ρv2/2 + ρgh + p = const
ρv2/2 is
ρgh is hydraulic head
p = static pressure
Слайд 14Hagen–Poiseuille law
flow of liquid depends on following factors: like the
Q = ΔP πr4/8ηL
Assumptions:
The tube is stiff, straight, and uniform
Liquid is Newtonian , i.e., viscosity is constant
The flow is laminar and steady, not pulsatile, and the velocity at the wall is zero (no slip at the wall)
Слайд 15Hagen–Poiseuille law
The Pressure Gradient (∆P) : Shows the difference in the
Radius of tube: The liquid flow varies directly with the radius to the power 4.
Viscosity (η): The flow of the fluid varies inversely with the viscosity of the fluid and as the viscosity of the fluid increases, the flow decreases vice versa.
Length of the Tube (L): The liquid flow is inversely proportional to the length of the tube, therefore longer the tube, greater is the resistance to the flow.
Resistance(R): The resistance is described by 8ηL/πr4 and therefore the Poiseuille’s law becomes
Q = ΔPπr4 / 8ηL
Q= (ΔP)/R
Слайд 16Cardiac output
Is the volume of blood being pumped by the
CO = HR × SV
Слайд 18Frank–Starling law
The Frank–Starling law of the heart represents the relationship between
Слайд 19Myocardial contractility
This results in better ejection of the blood in the
Controlled by extrinsic factors
sympathetic stimulation of the heart
hormones
K+ and Ca++ channel blockers
Myocardial contractility (cardiac inotropy) represents the innate ability of the heart muscle to contract. Changes in the ability to produce force during contraction result from incremental degrees of binding between thick and thin filaments.
Слайд 20Preload
Preload is the end diastolic volume that stretches the right or
Слайд 21Afterload
Afterload is the stress in the wall of the left ventricle
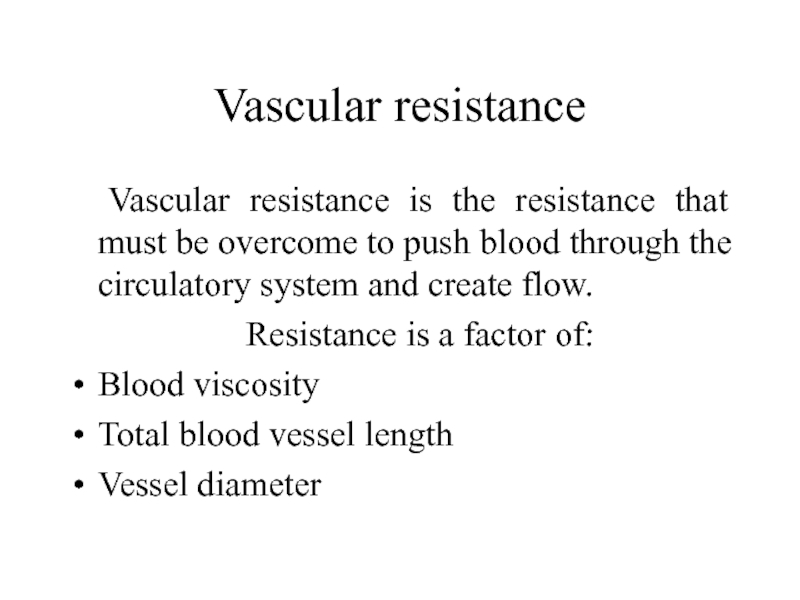
Слайд 22Vascular resistance
Vascular resistance is the resistance that must be overcome to
Resistance is a factor of:
Blood viscosity
Total blood vessel length
Vessel diameter
Слайд 23Rouleaux
Rouleaux are stacks or aggregations of red blood cells which form
Слайд 27Hagen–Poiseuille law
Pressure gradient: created by the heart.
Resistance
Radius of tube: diameter
Viscosity : property of blood.
Length of the tube
Q = ΔPπr4 / 8ηL
Q= (ΔP)/R








![Reynolds numberwherein: vs - mean fluid velocity, [m/s] L - characteristic length, [m] μ -](/img/tmb/4/326868/60eab77c23059f534e46d0fe235d131c-800x.jpg)