- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электротехника и электроника. Трехфазные цепи презентация
Содержание
- 1. Электротехника и электроника. Трехфазные цепи
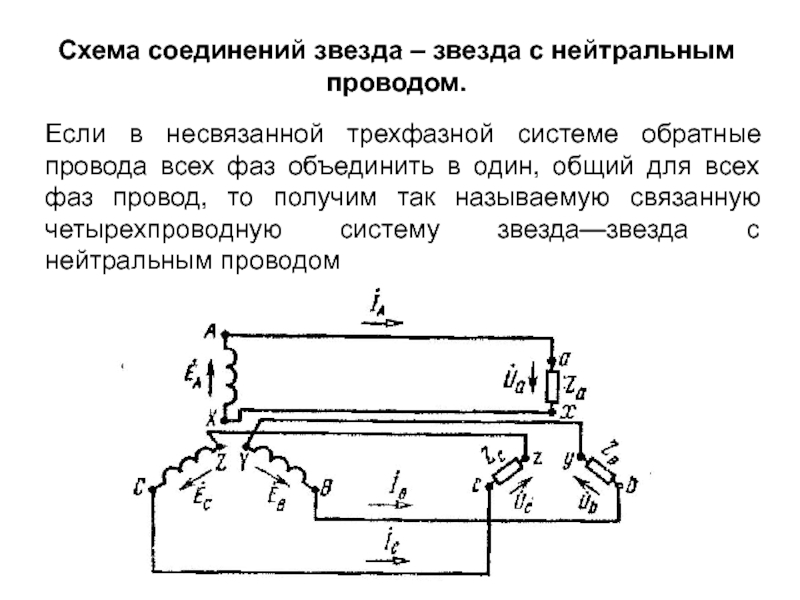
- 2. Схема соединений звезда – звезда с нейтральным
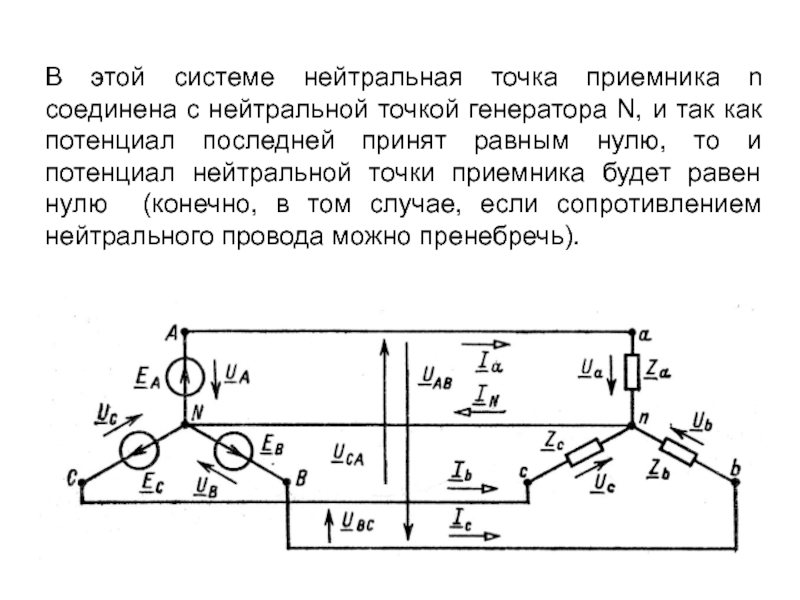
- 3. В этой системе нейтральная точка приемника n
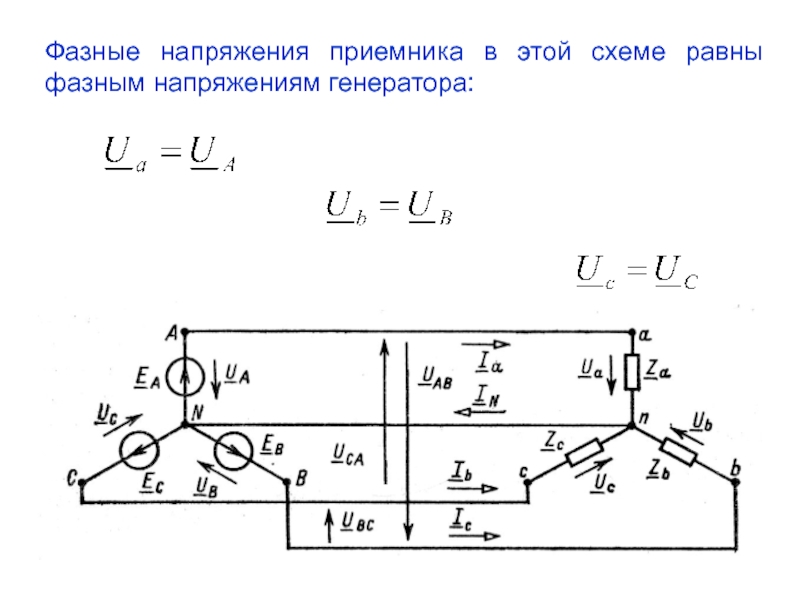
- 4. Фазные напряжения приемника в этой схеме равны фазным напряжениям генератора:
- 5. Соответственно равны и линейные напряжения (сопротивление всех
- 6. Токи при несимметричной нагрузке.
- 7. Токи при несимметричной нагрузке.
- 8. Токи при несимметричной нагрузке.
- 9. Токи при несимметричной нагрузке.
- 10. Токи при симметричной нагрузке.
- 11. При симметричной нагрузке расчет
- 12. При симметричной нагрузке расчет
- 13. Их сумма
- 25. Схема соединений звезда – звезда без нейтрального
- 26. Схема соединений звезда – звезда без нейтрального
- 27. Схема соединений звезда – звезда без нейтрального
- 28. Схема соединений звезда – звезда без нейтрального
- 29. Схема соединений звезда – звезда без нейтрального
- 30. Схема соединений звезда – звезда без нейтрального
- 31. Схема соединений звезда – звезда без нейтрального
- 32. Схема соединений звезда – звезда без нейтрального
- 33. Схема соединений звезда – звезда без нейтрального
- 34. Схема соединений звезда – звезда без нейтрального
- 35. Схема соединения потребителей в треугольник.
- 36. Схема соединения потребителей в треугольник.
- 37. Схема соединения потребителей в треугольник.
- 38. Схема соединения потребителей в треугольник.
- 39. Схема соединения потребителей в треугольник.
- 40. Схема соединения потребителей в треугольник.
- 41. Схема соединения потребителей в треугольник.
- 42. Схема соединения потребителей в треугольник.
- 56. Мощность
- 58. Коэффициент мощности трехфазных симметричных приемников. Значительную часть
- 59. Коэффициент мощности трехфазных симметричных приемников. При загрузке
- 60. Коэффициент мощности трехфазных симметричных приемников. Улучшение коэффициента
- 61. Коэффициент мощности трехфазных симметричных приемников. Коэффициент мощности
- 62. Коэффициент мощности трехфазных симметричных приемников. Из
- 63. Техника безопасности при эксплуатации трехфазных цепей
- 64. Техника безопасности при эксплуатации трехфазных цепей
- 65. Техника безопасности при эксплуатации трехфазных цепей
- 66. Техника безопасности при эксплуатации трехфазных цепей
- 67. Техника безопасности при эксплуатации трехфазных цепей
- 68. Техника безопасности при эксплуатации трехфазных цепей
- 69. Техника безопасности при эксплуатации трехфазных цепей
- 70. Задание 2.Часть Б. Расчет трехфазных сетей.
- 71. Задание 2.Часть Б. Расчет трехфазных сетей.
- 72. Задание 2.Часть Б. Расчет трехфазных сетей.
- 73. Задание 2.Часть Б. Расчет трехфазных сетей.
- 74. Задание 2.Часть Б. Расчет трехфазных сетей.
- 75. Задание 2.Часть Б. Расчет трехфазных сетей.
- 76. Задание 2.Часть Б. Расчет трехфазных сетей.
- 78. Задание 2.Часть Б. Расчет трехфазных сетей.
- 79. Задание 2.Часть Б. Расчет трехфазных сетей.
- 80. Задание 2.Часть Б. Расчет трехфазных сетей.
- 81. Задание 2.Часть Б. Расчет трехфазных сетей.
- 82. Задание 2.Часть Б. Расчет трехфазных сетей.
- 83. Задание 2.Часть Б. Расчет трехфазных сетей.
- 84. Задание 2.Часть Б. Расчет трехфазных сетей.
- 85. Задание 2.Часть Б. Расчет трехфазных сетей.
- 86. Задание 2.Часть Б. Расчет трехфазных сетей.
- 87. Задание 2.Часть Б. Расчет трехфазных сетей.
- 88. Задание 2.Часть Б. Расчет трехфазных сетей.
- 89. Задание 2.Часть Б. Расчет трехфазных сетей.
- 90. Задание 2.Часть Б. Расчет трехфазных сетей.
- 92. Задание 2.Часть Б. Расчет трехфазных сетей.
- 93. Задание 2.Часть Б. Расчет трехфазных сетей.
- 94. Задание 2.Часть Б. Расчет трехфазных сетей.
- 95. Задание 2.Часть Б. Расчет трехфазных сетей.
- 96. Задание 2.Часть Б. Расчет трехфазных сетей.
- 98. Задание 2.Часть Б. Расчет трехфазных сетей.
- 99. Задание 2.Часть Б. Расчет трехфазных сетей.
- 100. Задание 2.Часть Б. Расчет трехфазных сетей.
- 101. Задание 2.Часть Б. Расчет трехфазных сетей.
- 102. Задание 2.Часть Б. Расчет трехфазных сетей.
- 103. Задание 2.Часть Б. Расчет трехфазных сетей.
- 104. Задание 2.Часть Б. Расчет трехфазных сетей.
- 105. Задание 2.Часть Б. Расчет трехфазных сетей.
- 107. Задание 2.Часть Б. Расчет трехфазных сетей.
- 108. Задание 2.Часть Б. Расчет трехфазных сетей.
- 109. Задание 2.Часть Б. Расчет трехфазных сетей.
- 110. Задание 2.Часть Б. Расчет трехфазных сетей.
- 111. Задание 2.Часть Б. Расчет трехфазных сетей.
- 112. Задание 2.Часть Б. Расчет трехфазных сетей.
- 114. Задание 2.Часть Б. Расчет трехфазных сетей.
- 115. Задание 2.Часть Б. Расчет трехфазных сетей.
- 116. Задание 2.Часть Б. Расчет трехфазных сетей.
- 117. Задание 2.Часть Б. Расчет трехфазных сетей.
- 118. Задание 2.Часть Б. Расчет трехфазных сетей.
- 119. Задание 2.Часть Б. Расчет трехфазных сетей.
- 120. Задание 2.Часть Б. Расчет трехфазных сетей.
- 121. Задание 2.Часть Б. Расчет трехфазных сетей.
- 122. Задание 2.Часть Б. Расчет трехфазных сетей.
- 123. Задание 2.Часть Б. Расчет трехфазных сетей.
- 124. Задание 2.Часть Б. Расчет трехфазных сетей.
- 125. Задание 2.Часть Б. Расчет трехфазных сетей.
Слайд 2Схема соединений звезда – звезда с нейтральным проводом.
Если в несвязанной
Слайд 3В этой системе нейтральная точка приемника n соединена с нейтральной точкой
Слайд 5Соответственно равны и линейные напряжения (сопротивление всех проводов принято равным нулю)
или в общем виде
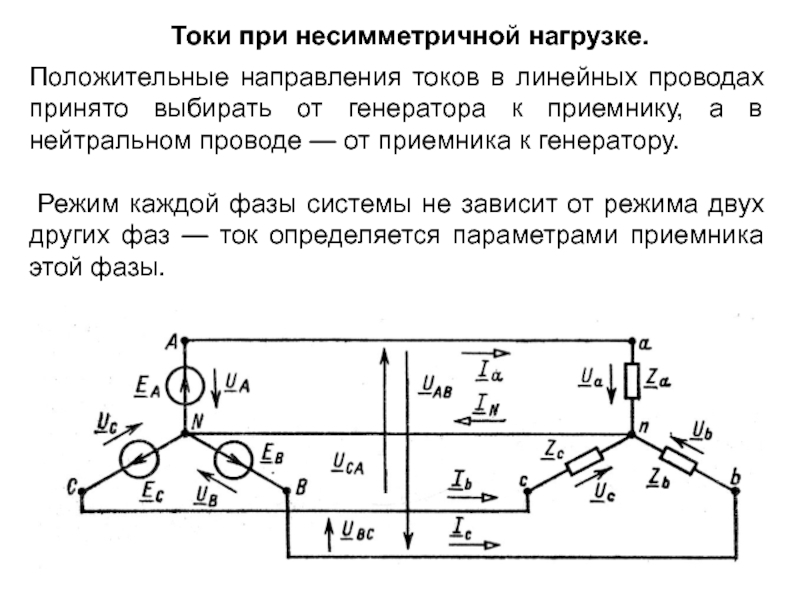
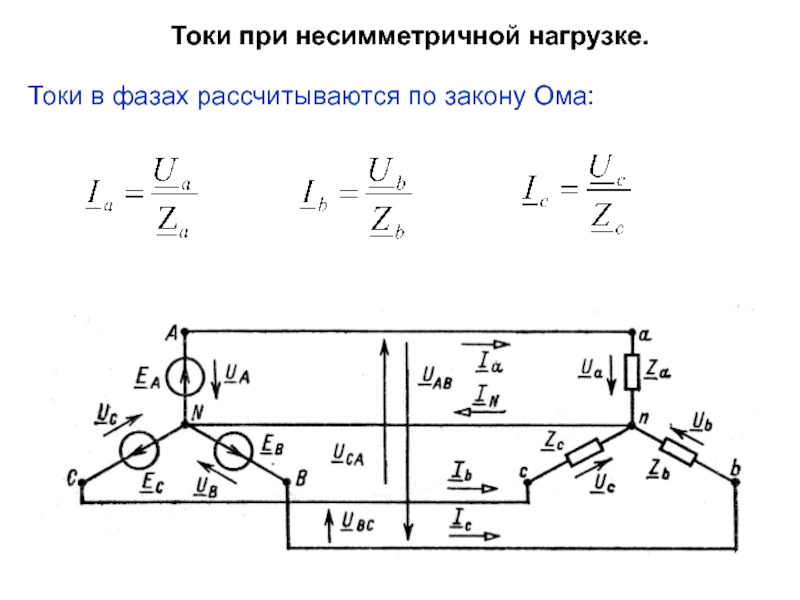
Слайд 6Токи при несимметричной нагрузке.
Положительные направления токов в линейных проводах принято
Режим каждой фазы системы не зависит от режима двух других фаз — ток определяется параметрами приемника этой фазы.
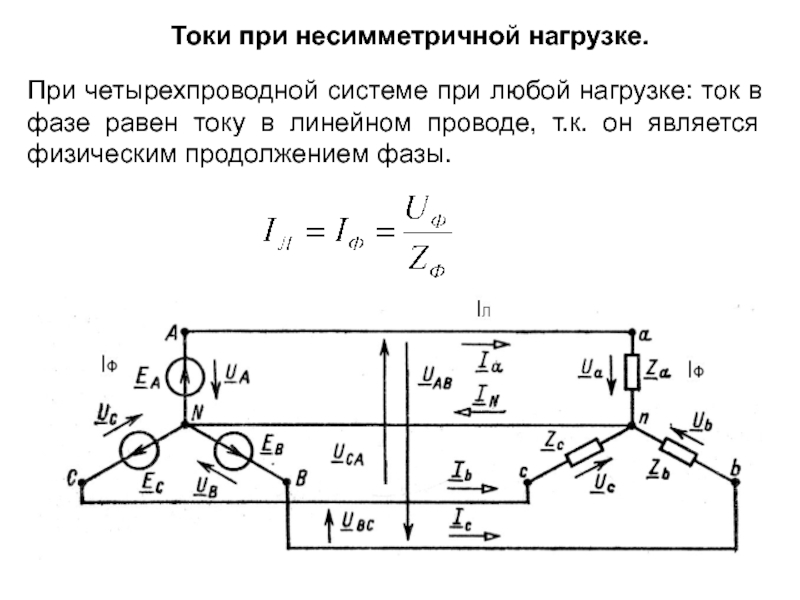
Слайд 8Токи при несимметричной нагрузке.
При четырехпроводной системе при любой нагрузке: ток
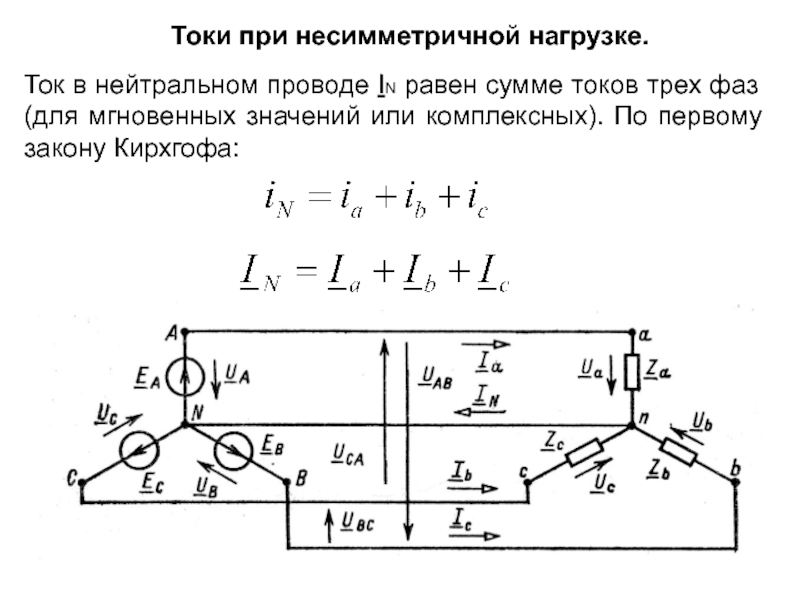
Слайд 9Токи при несимметричной нагрузке.
Ток в нейтральном проводе IN равен сумме
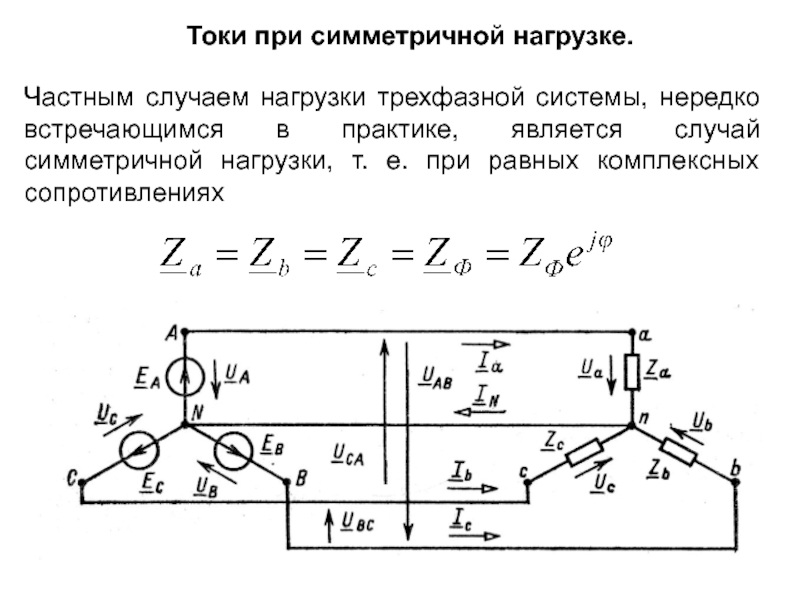
Слайд 10Токи при симметричной нагрузке.
Частным случаем нагрузки трехфазной системы, нередко встречающимся
Слайд 11
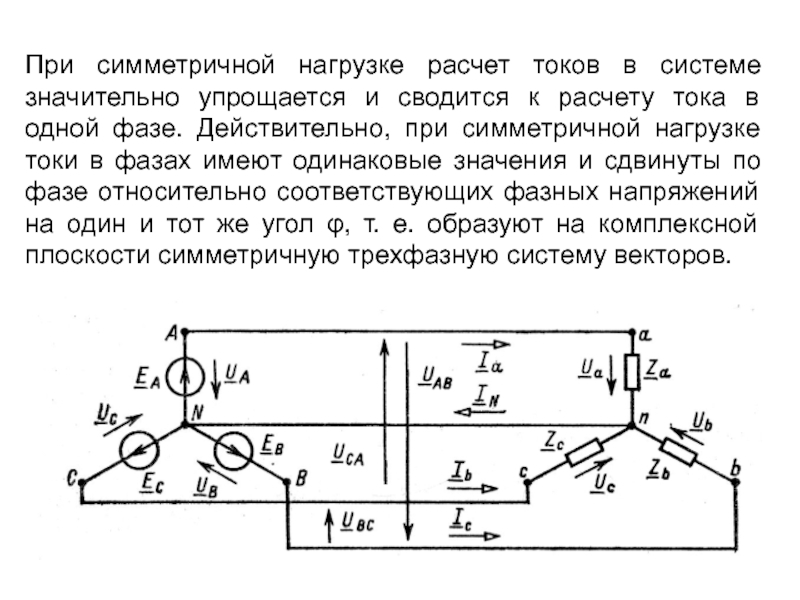
При симметричной нагрузке расчет токов в системе значительно упрощается и сводится
Слайд 12
При симметричной нагрузке расчет токов в системе значительно упрощается и сводится
Фазные напряжения
Линейные напряжения
Слайд 13
Их сумма
Это равенство означает, что при симметричной нагрузке ток
Слайд 14
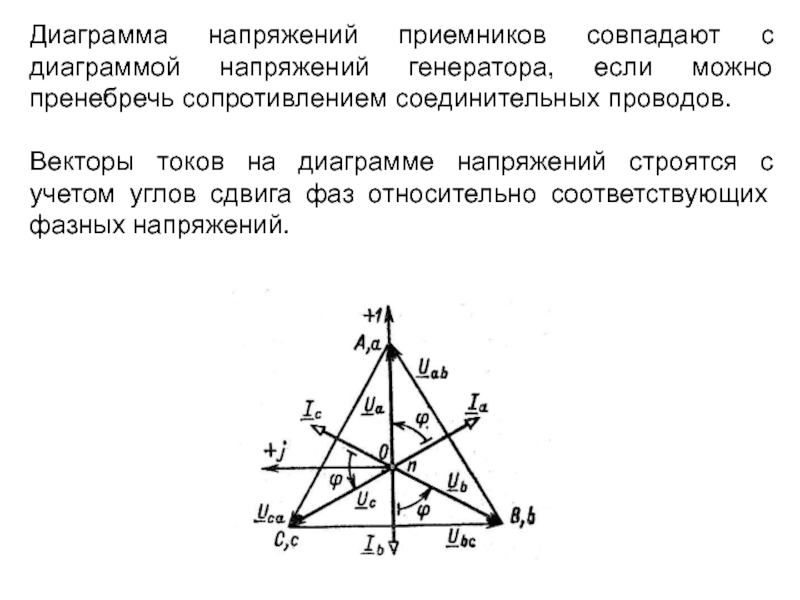
Диаграмма напряжений приемников совпадают с диаграммой напряжений генератора, если можно пренебречь
Векторы токов на диаграмме напряжений строятся с учетом углов сдвига фаз относительно соответствующих фазных напряжений.
Слайд 15
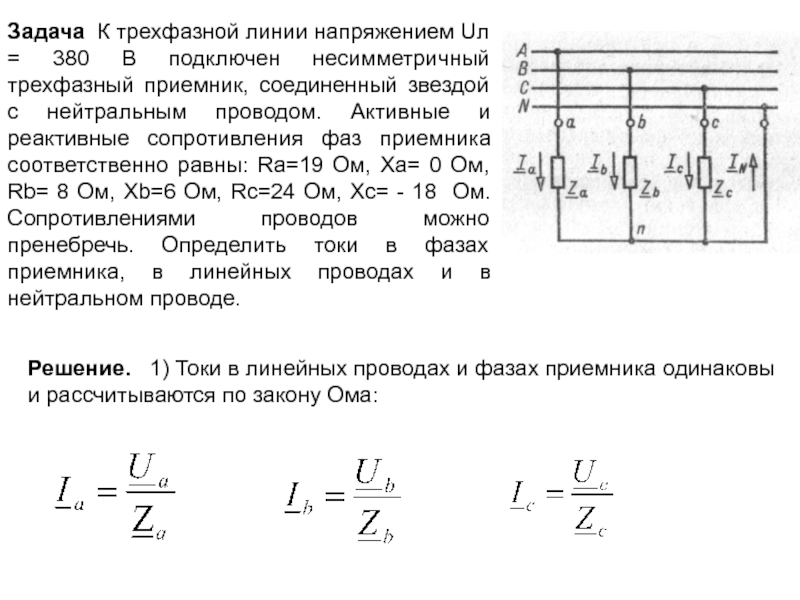
Задача К трехфазной линии напряжением Uл = 380 В подключен несимметричный
Решение. 1) Токи в линейных проводах и фазах приемника одинаковы и рассчитываются по закону Ома:
Слайд 16
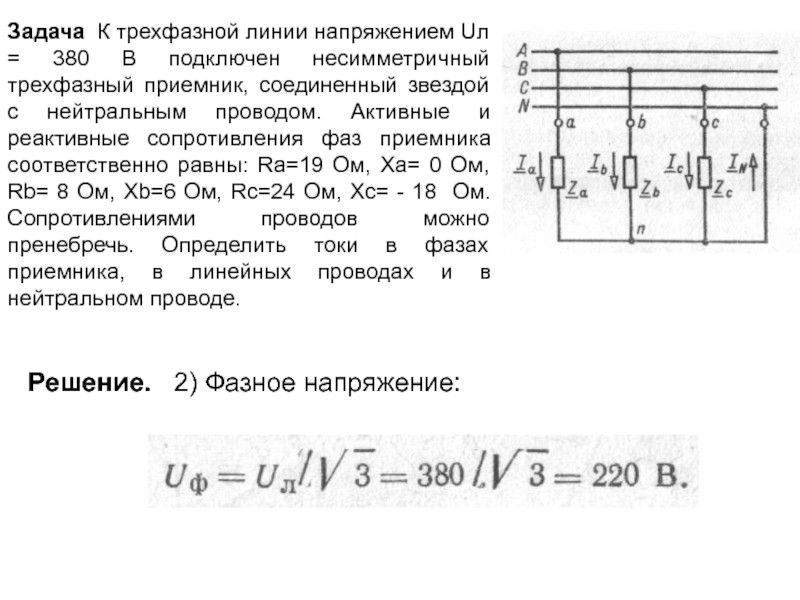
Задача К трехфазной линии напряжением Uл = 380 В подключен несимметричный
Решение. 2) Фазное напряжение:
Слайд 17
Задача К трехфазной линии напряжением Uл = 380 В подключен несимметричный
Решение. 3) Комплексные фазные напряжения:
Слайд 18
Задача К трехфазной линии напряжением Uл = 380 В подключен несимметричный
Решение. 4) Комплексные сопротивления фаз:
Слайд 19
Задача К трехфазной линии напряжением Uл = 380 В подключен несимметричный
Решение. 5) Токи в фазах приемника и проводах линии:
Слайд 20
Задача К трехфазной линии напряжением Uл = 380 В подключен несимметричный
Решение. 6) Ток в нейтральном проводе
Слайд 21
Задача К трехфазной линии напряжением Uл = 380 В подключен несимметричный
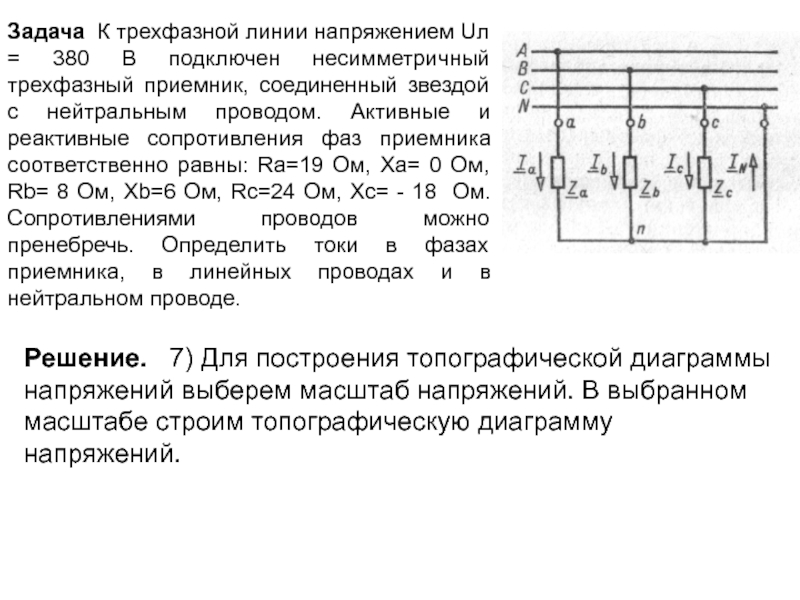
Решение. 7) Для построения топографической диаграммы напряжений выберем масштаб напряжений. В выбранном масштабе строим топографическую диаграмму напряжений.
Слайд 22
Задача К трехфазной линии напряжением Uл = 380 В подключен несимметричный
Решение. 7) При построении векторной диаграммы токов учтем, что токи в фазах сдвинуты относительно фазных напряжений на разные углы сдвига фаз: φа = 0 - нагрузка чисто активная,
φb=36°52' - нагрузка активно-индуктивная,
φс= - 36°52' - нагрузка активно-емкостная.
Слайд 23
Задача К трехфазной линии напряжением Uл = 380 В подключен несимметричный
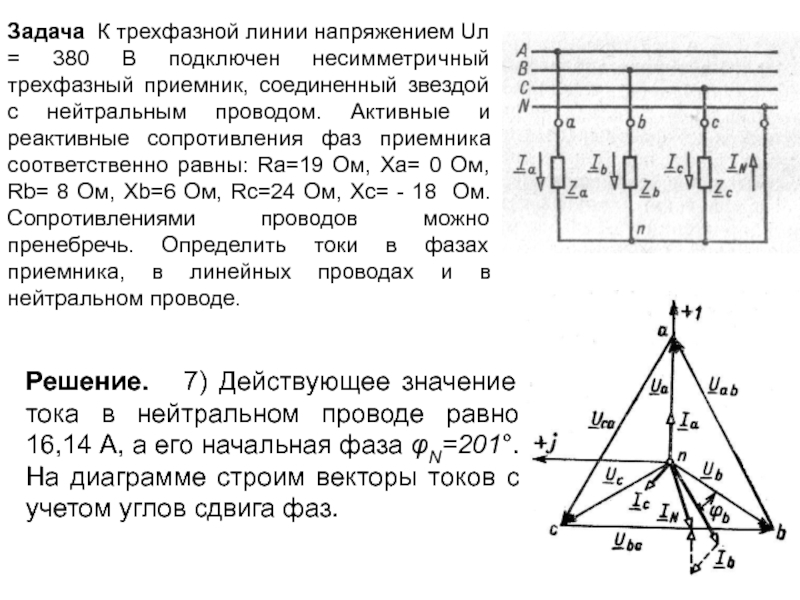
Решение. 7) Действующее значение тока в нейтральном проводе равно 16,14 А, a eгo начальная фаза φN=201°. На диаграмме строим векторы токов с учетом углов сдвига фаз.
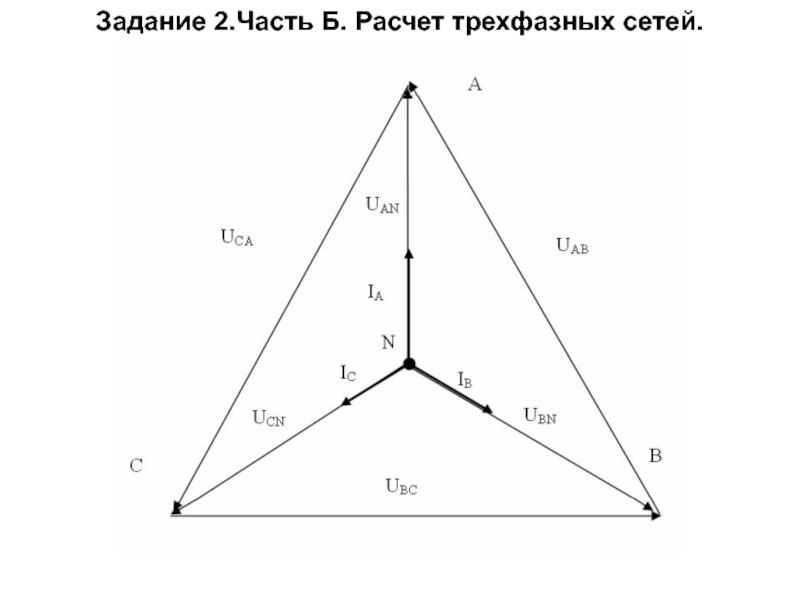
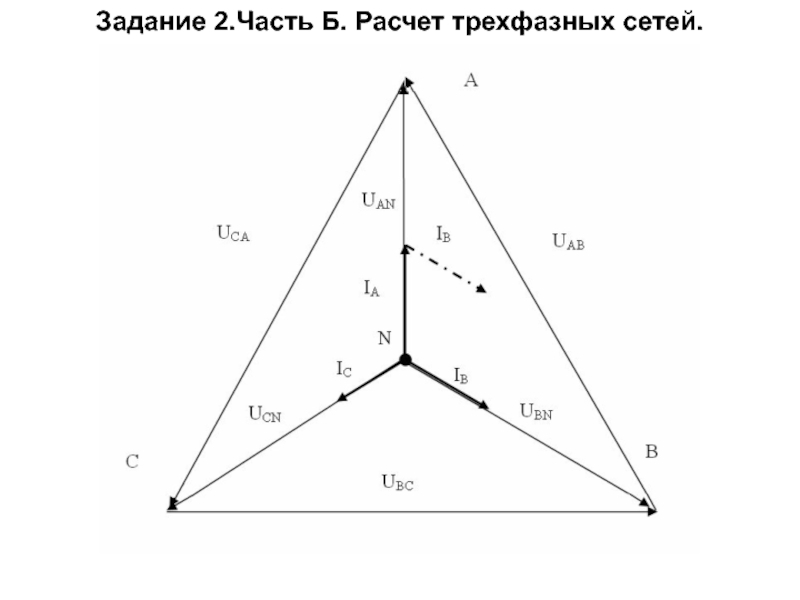
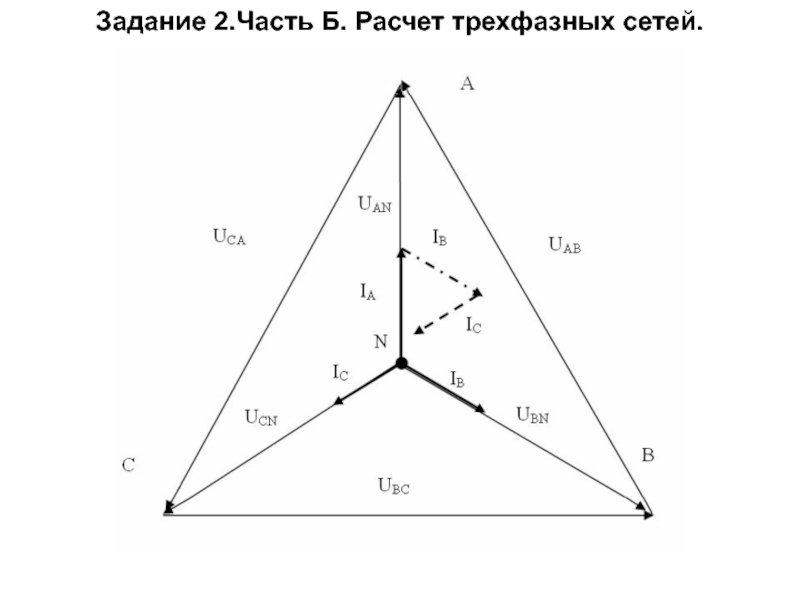
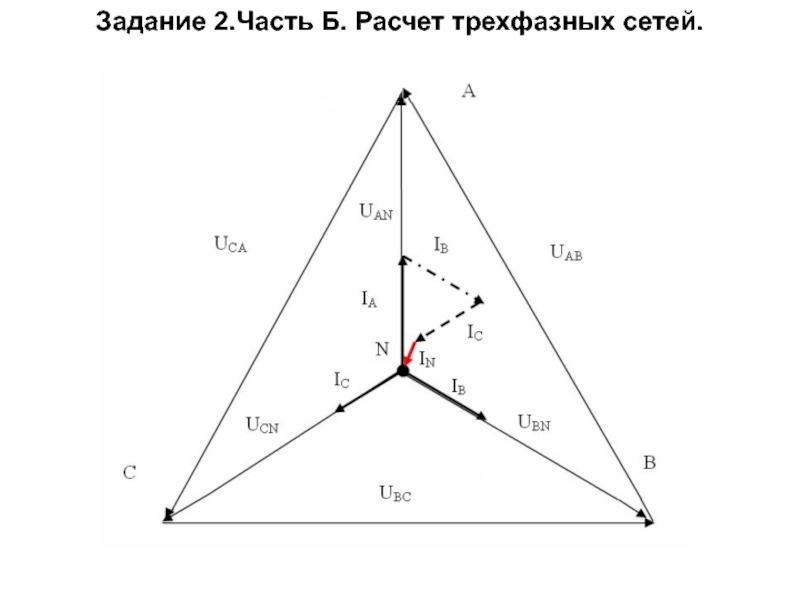
Слайд 24
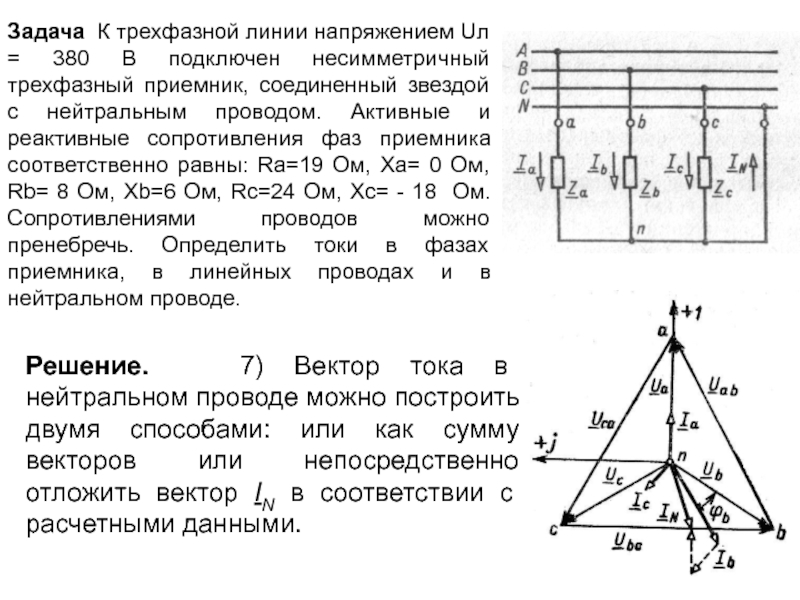
Задача К трехфазной линии напряжением Uл = 380 В подключен несимметричный
Решение. 7) Вектор тока в нейтральном проводе можно построить двумя способами: или как сумму векторов или непосредственно отложить вектор IN в соответствии с расчетными данными.
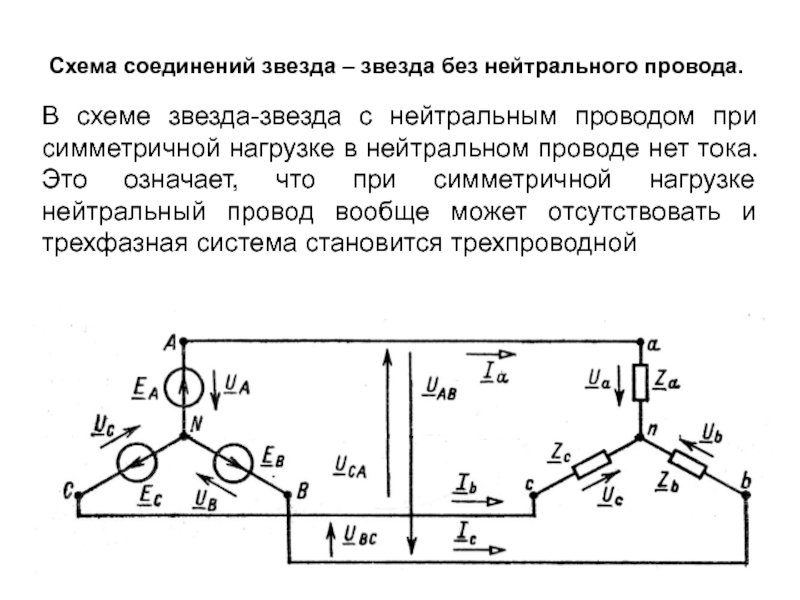
Слайд 25Схема соединений звезда – звезда без нейтрального провода.
В схеме звезда-звезда
Слайд 26Схема соединений звезда – звезда без нейтрального провода.
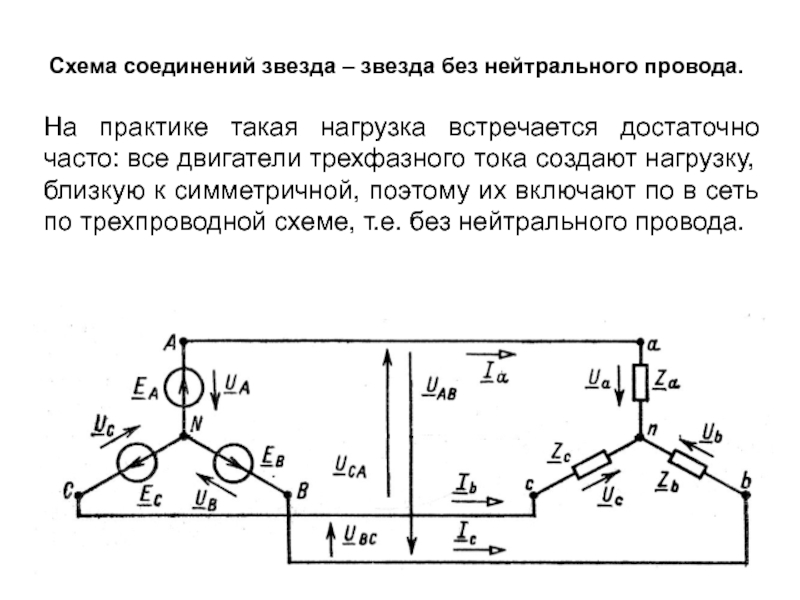
На практике такая
Слайд 27Схема соединений звезда – звезда без нейтрального провода.
Расчет токов трехпроводной
в данном случае ничем не отличается от расчета токов в четырехпроводной системе звезда-звезда с нейтральным проводом и ведется на одну фазу
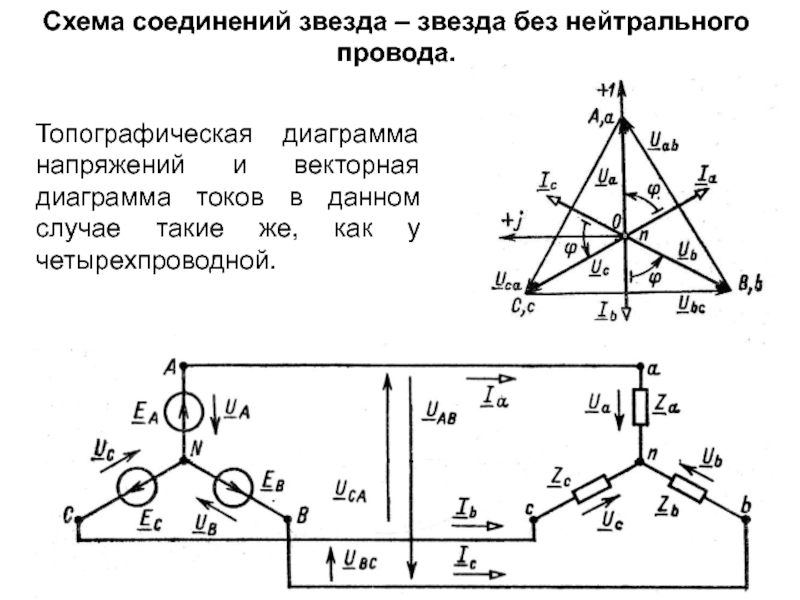
Слайд 29Схема соединений звезда – звезда без нейтрального провода.
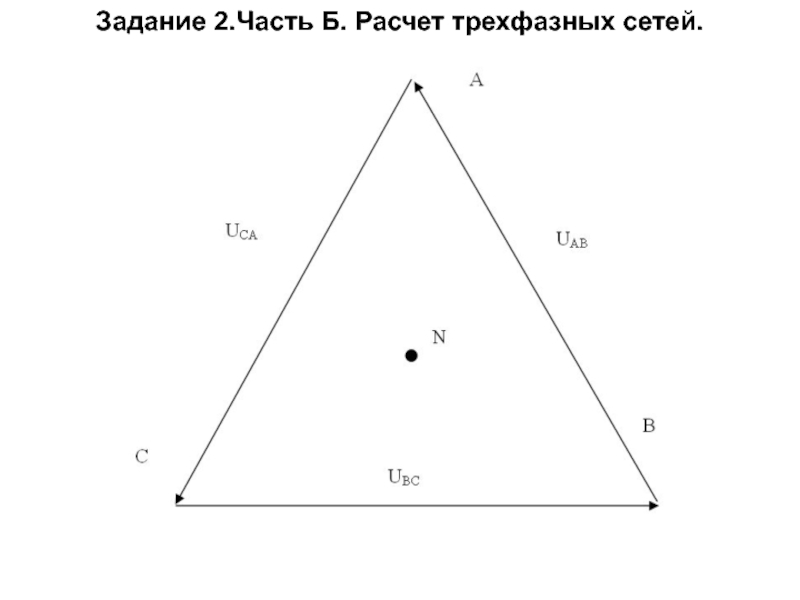
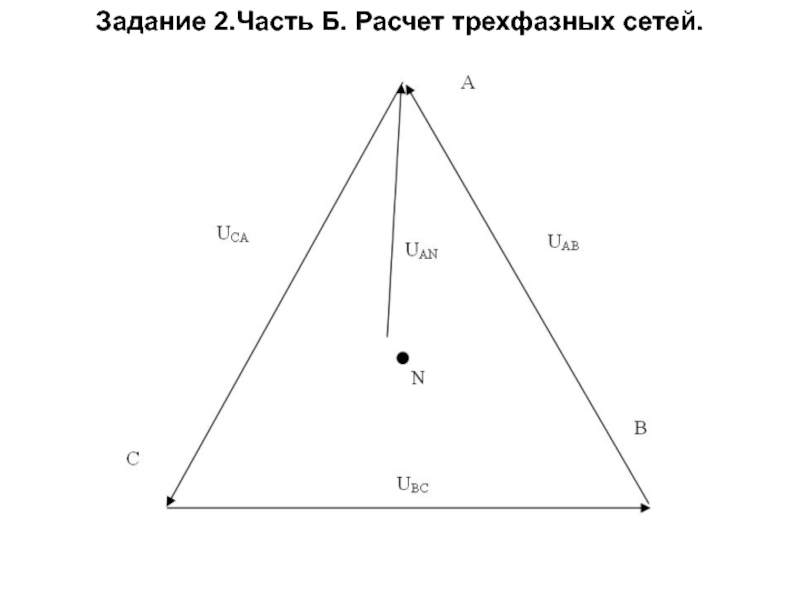
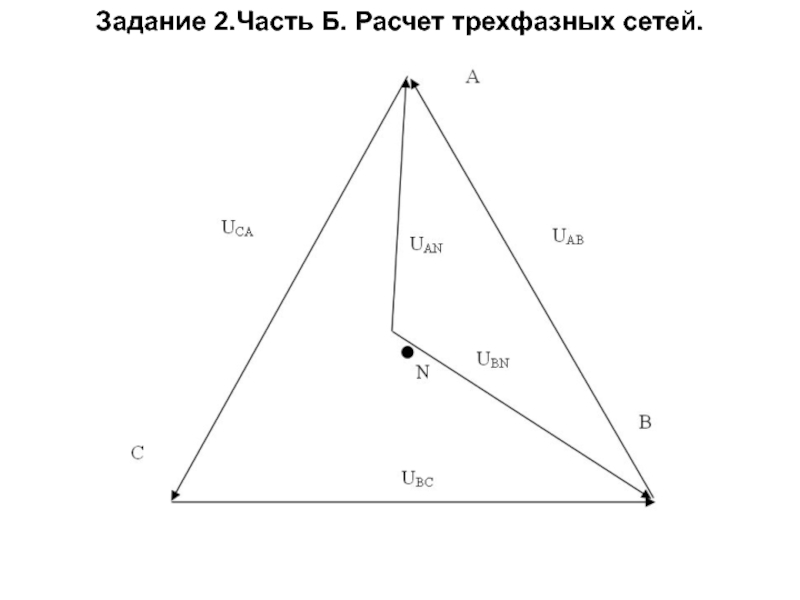
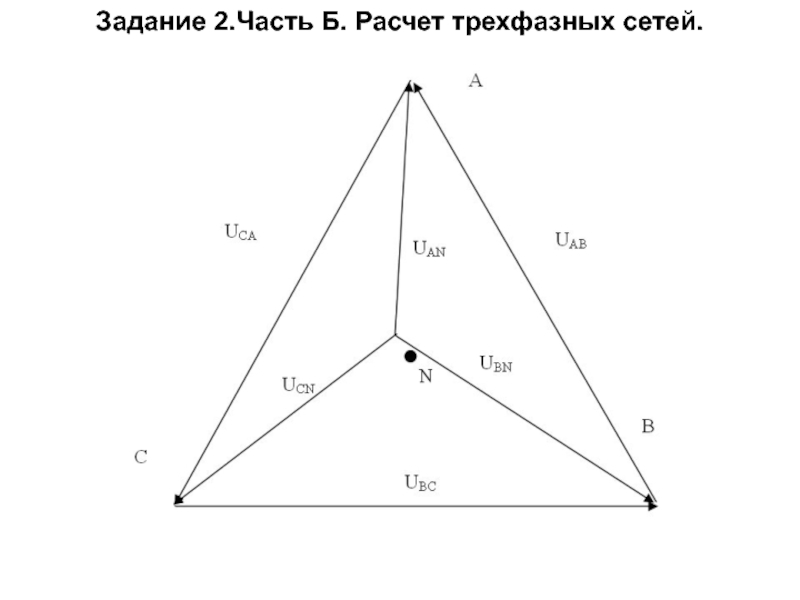
Топографическая диаграмма напряжений
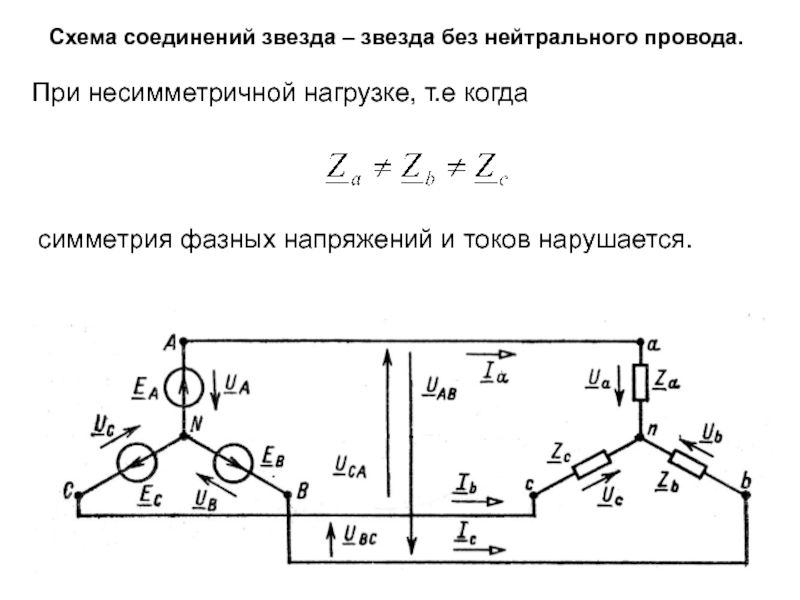
Слайд 30Схема соединений звезда – звезда без нейтрального провода.
При несимметричной нагрузке,
симметрия фазных напряжений и токов нарушается.
Слайд 31Схема соединений звезда – звезда без нейтрального провода.
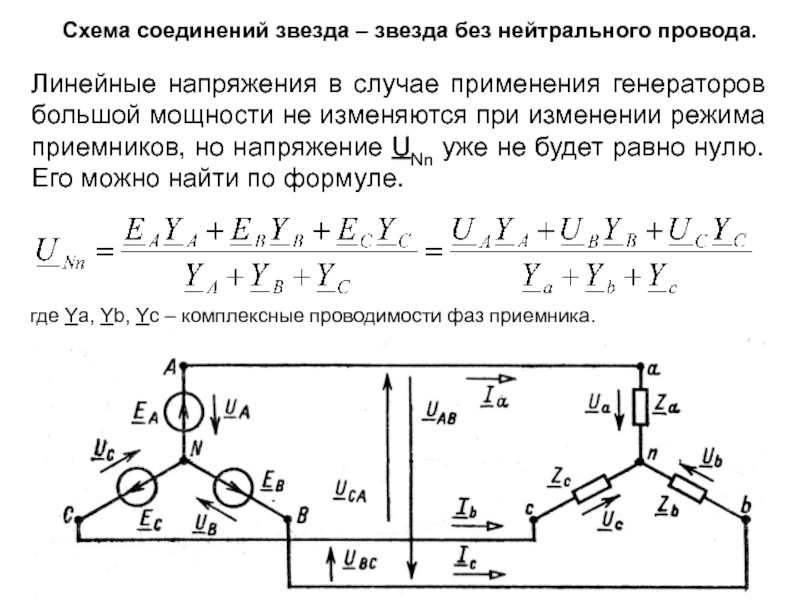
Линейные напряжения в
где Ya, Yb, Yc – комплексные проводимости фаз приемника.
Слайд 32Схема соединений звезда – звезда без нейтрального провода.
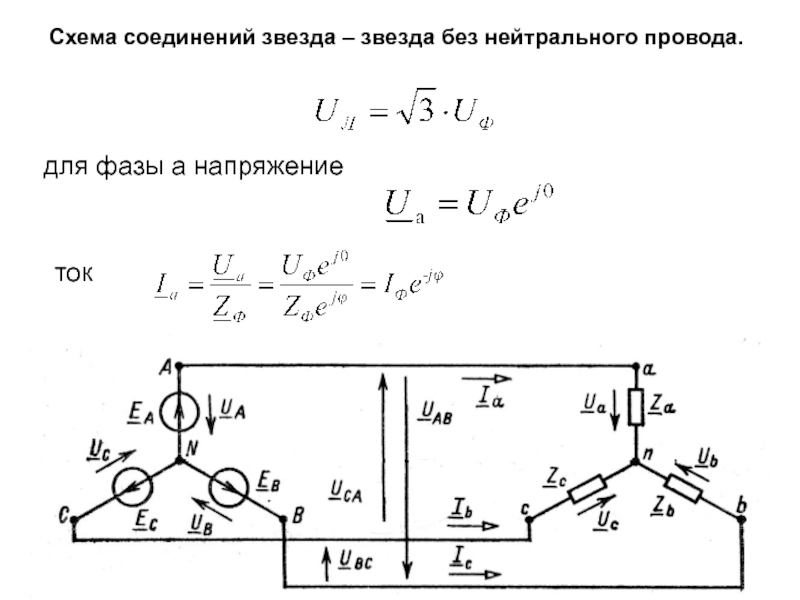
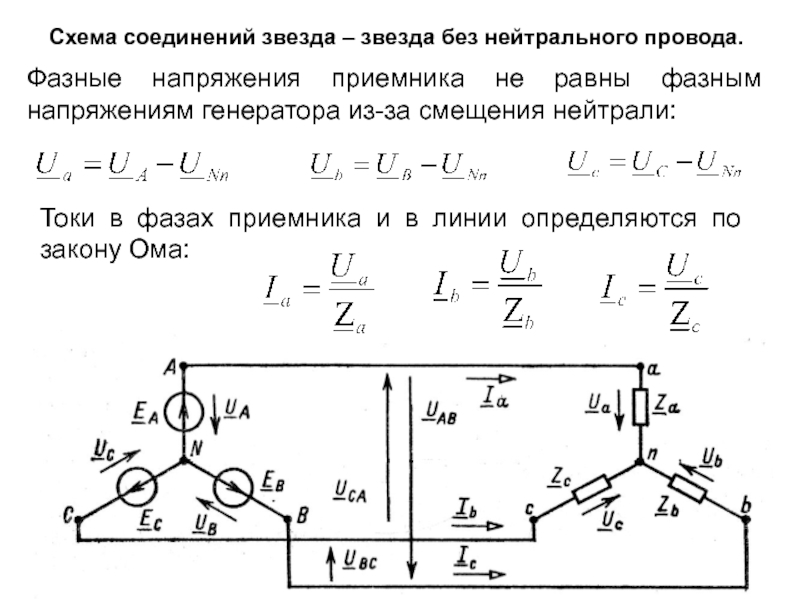
Фазные напряжения приемника
Токи в фазах приемника и в линии определяются по закону Ома:
Слайд 33Схема соединений звезда – звезда без нейтрального провода.
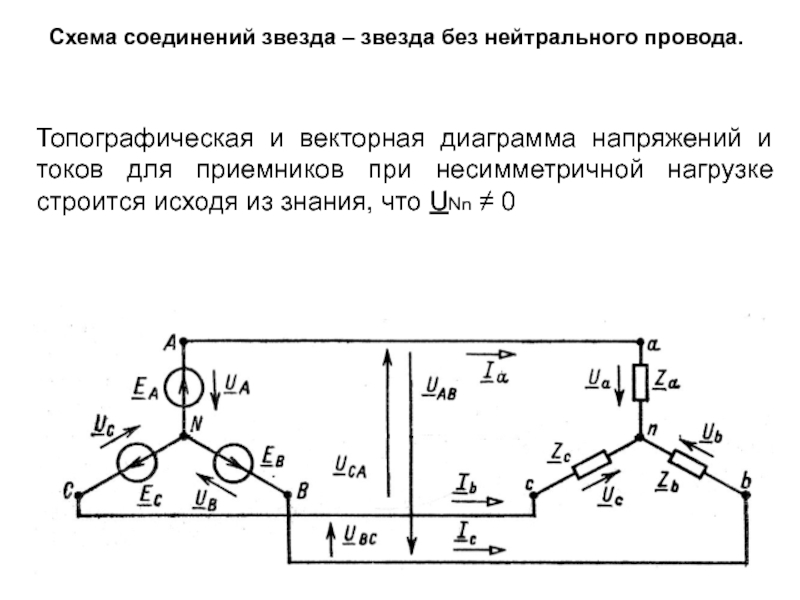
Топографическая и векторная
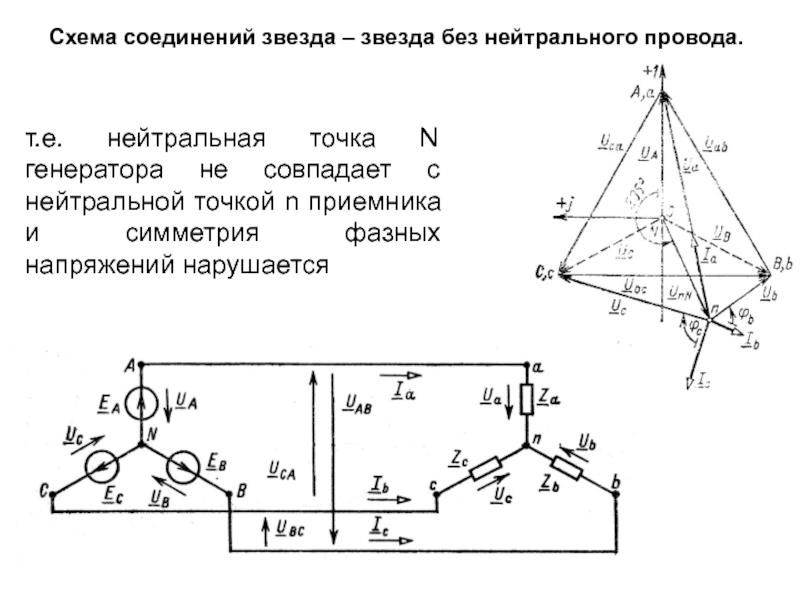
Слайд 34Схема соединений звезда – звезда без нейтрального провода.
т.е. нейтральная точка
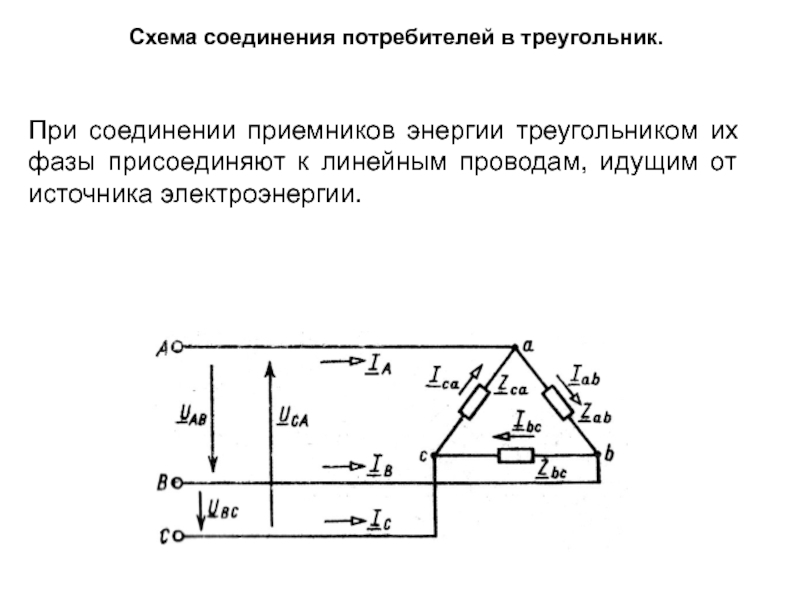
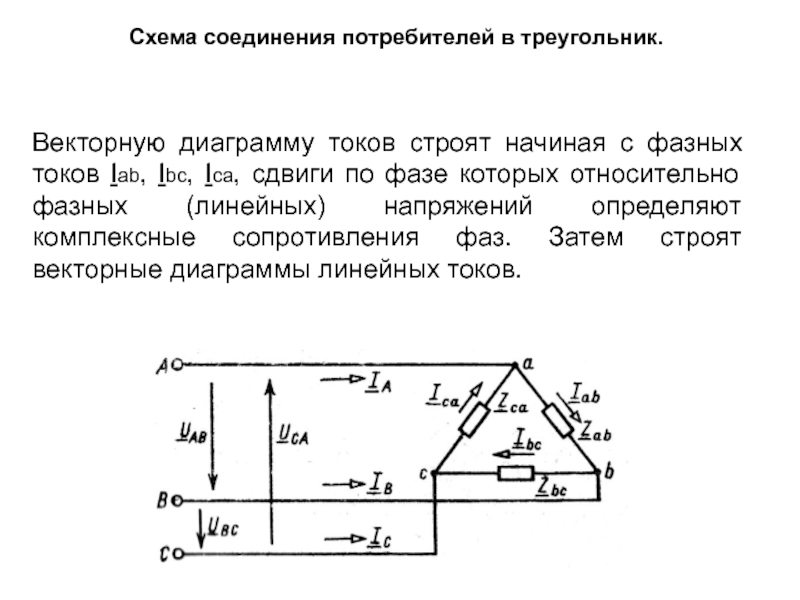
Слайд 35Схема соединения потребителей в треугольник.
При соединении приемников энергии треугольником их
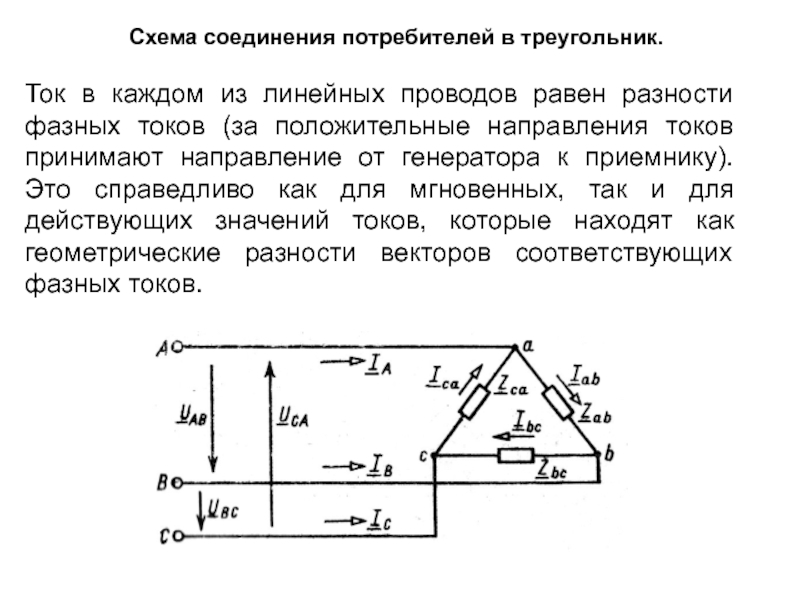
Слайд 36Схема соединения потребителей в треугольник.
Ток в каждом из линейных проводов
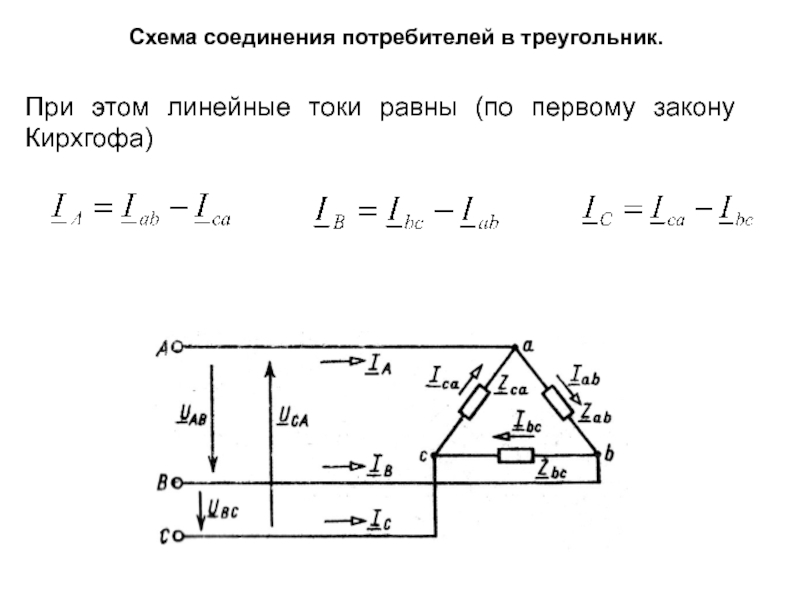
Слайд 37Схема соединения потребителей в треугольник.
При этом линейные токи равны (по
Слайд 39Схема соединения потребителей в треугольник.
Векторную диаграмму токов строят начиная с
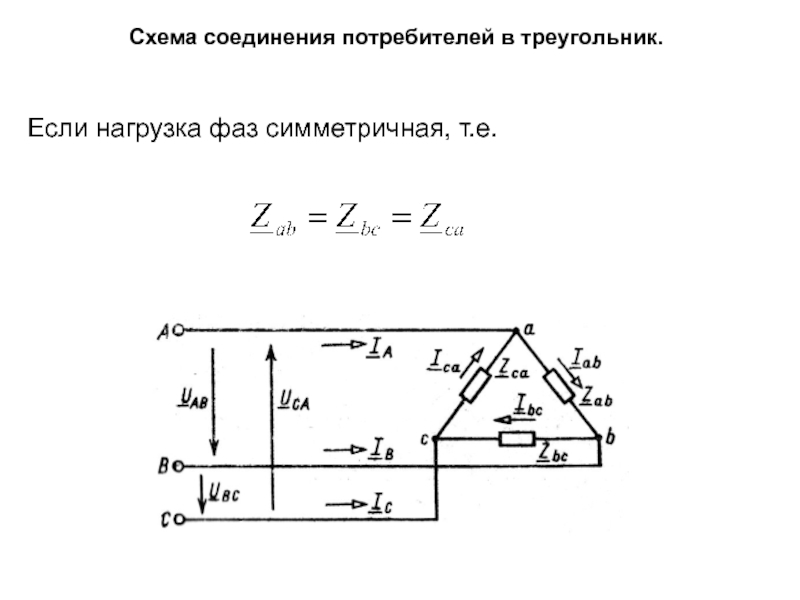
Слайд 41Схема соединения потребителей в треугольник.
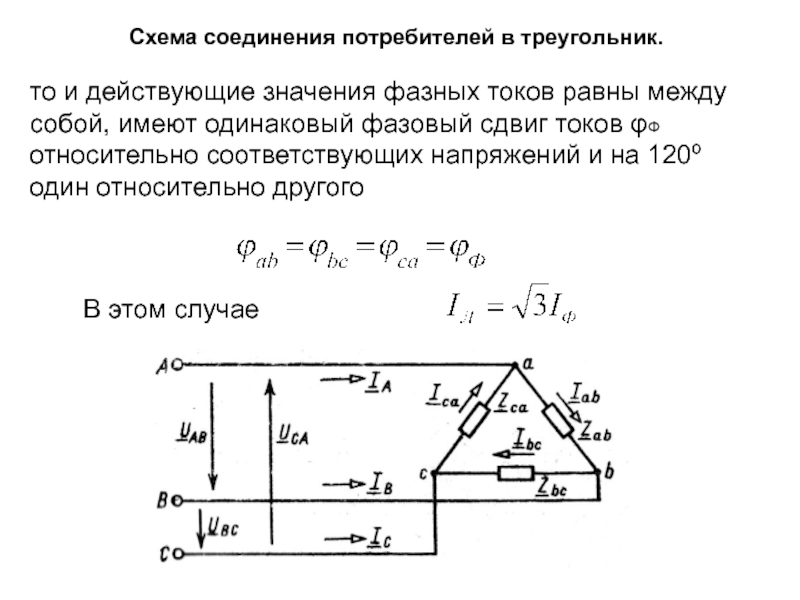
то и действующие значения фазных токов
В этом случае
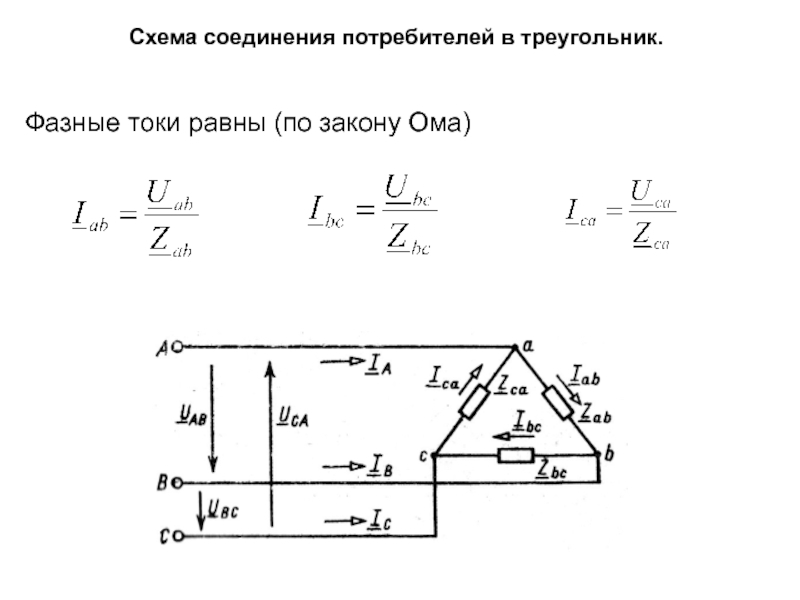
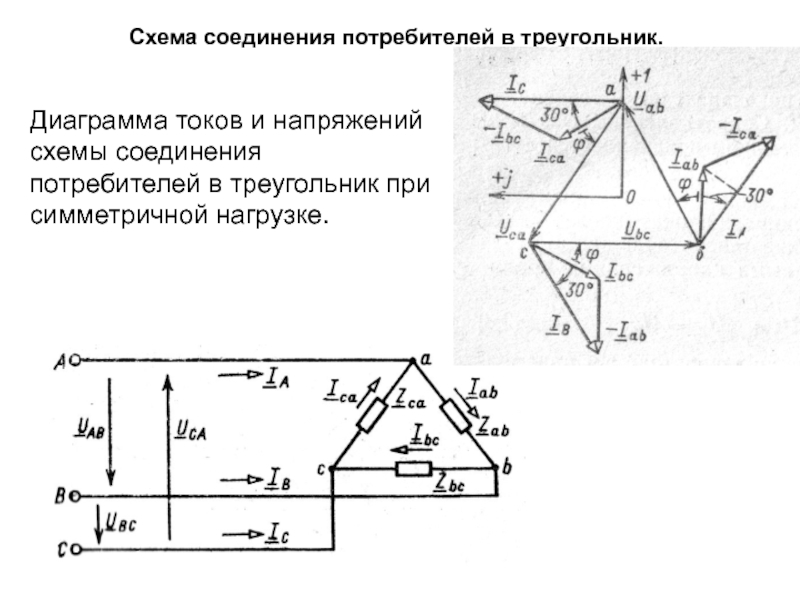
Слайд 42Схема соединения потребителей в треугольник.
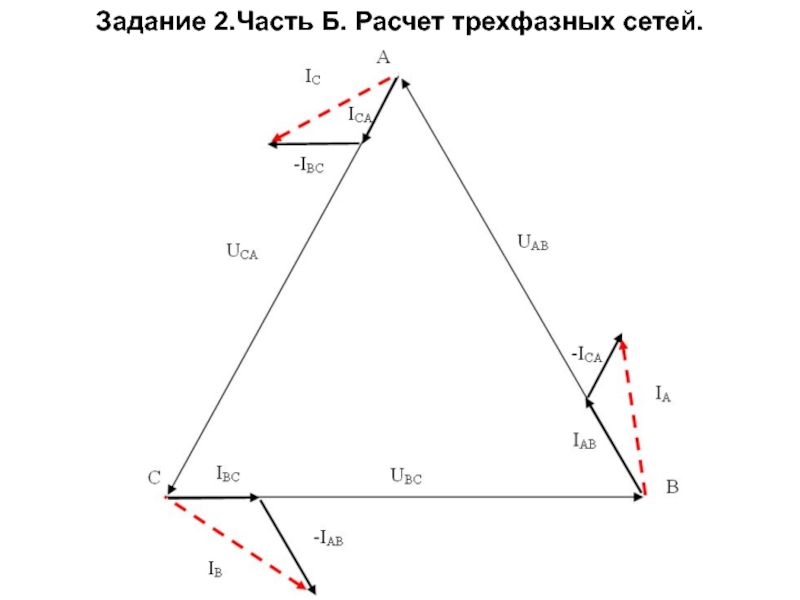
Диаграмма токов и напряжений схемы соединения
Слайд 43
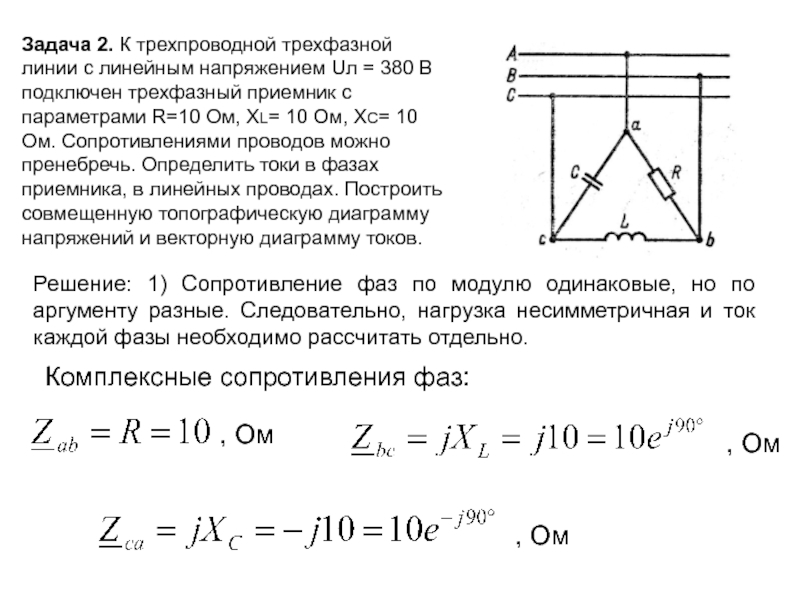
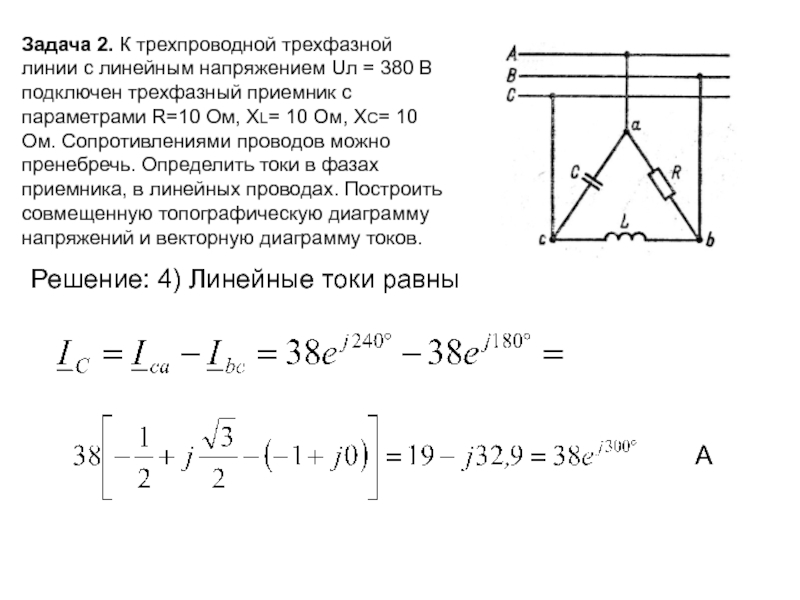
Задача 2. К трехпроводной трехфазной линии с линейным напряжением Uл =
Решение: 1) Сопротивление фаз по модулю одинаковые, но по аргументу разные. Следовательно, нагрузка несимметричная и ток каждой фазы необходимо рассчитать отдельно.
Комплексные сопротивления фаз:
, Ом
, Ом
, Ом
Слайд 44
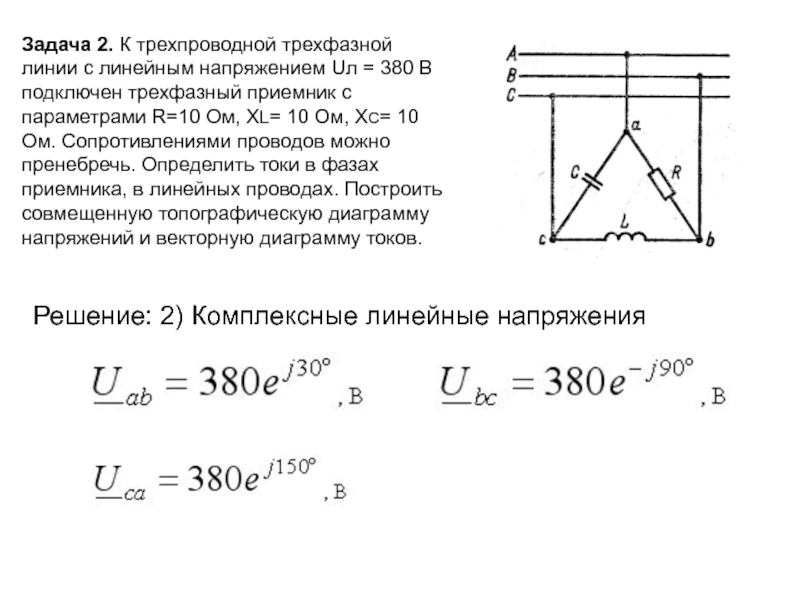
Задача 2. К трехпроводной трехфазной линии с линейным напряжением Uл =
Решение: 2) Комплексные линейные напряжения
Слайд 45
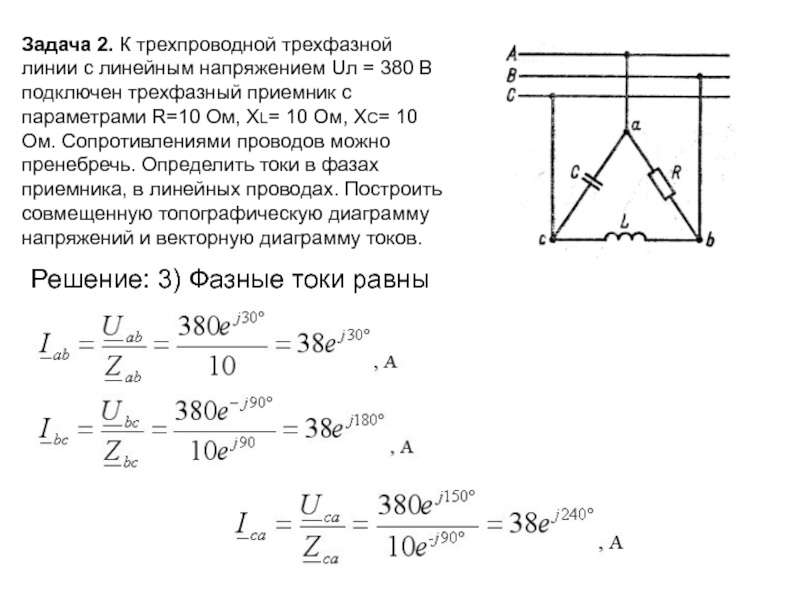
Задача 2. К трехпроводной трехфазной линии с линейным напряжением Uл =
Решение: 3) Фазные токи равны
Слайд 46
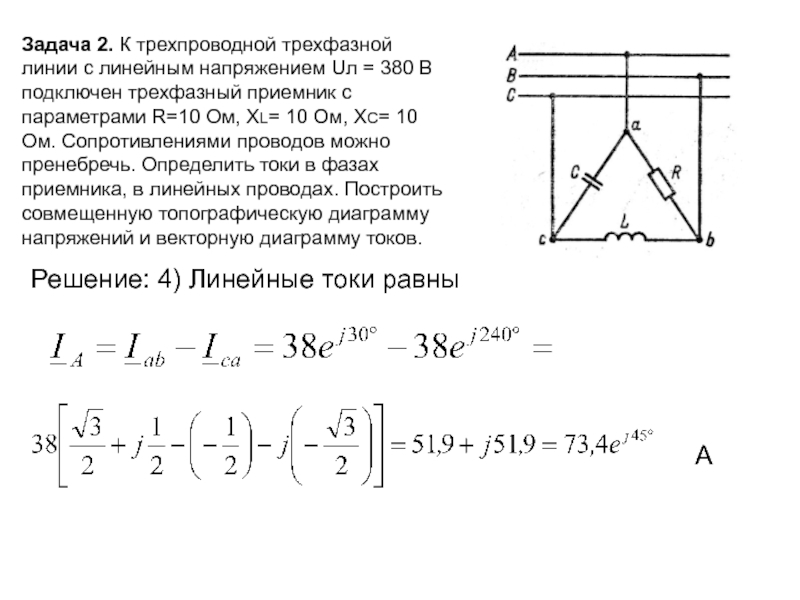
Задача 2. К трехпроводной трехфазной линии с линейным напряжением Uл =
Решение: 4) Линейные токи равны
А
Слайд 47
Задача 2. К трехпроводной трехфазной линии с линейным напряжением Uл =
Решение: 4) Линейные токи равны
А
Слайд 48
Задача 2. К трехпроводной трехфазной линии с линейным напряжением Uл =
Решение: 4) Линейные токи равны
А
Слайд 49
Задача 2. К трехпроводной трехфазной линии с линейным напряжением Uл =
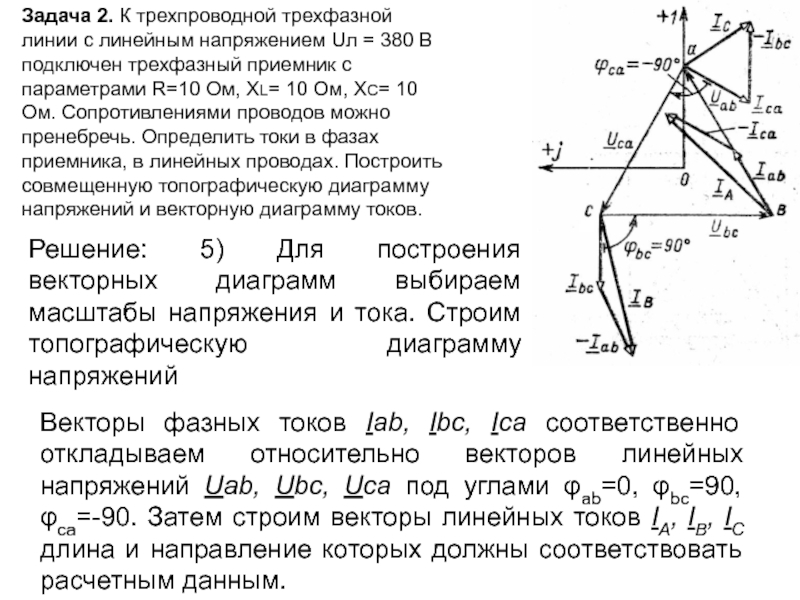
Решение: 5) Для построения векторных диаграмм выбираем масштабы напряжения и тока. Строим топографическую диаграмму напряжений
Векторы фазных токов Iab, Ibc, Ica соответственно откладываем относительно векторов линейных напряжений Uab, Ubc, Uca под углами φab=0, φbc=90, φca=-90. Затем строим векторы линейных токов IA, IB, IC длина и направление которых должны соответствовать расчетным данным.
Слайд 50
Задача 2. К трехпроводной трехфазной линии с линейным напряжением Uл =
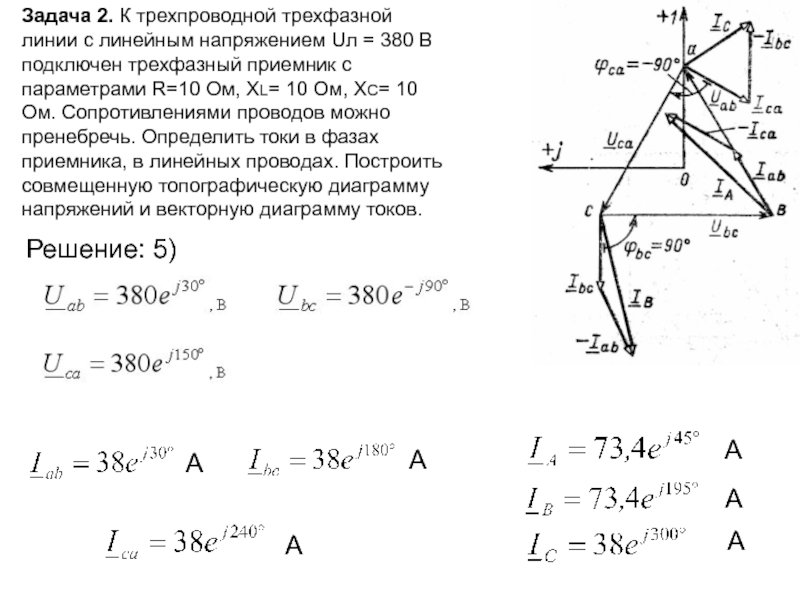
Решение: 5)
А
А
А
А
А
А
Слайд 51
Мощность трехфазной цепи.
Активная мощность
Так как трехфазная цепь представляет собой совокупность трех
Тогда среднее за период значение мощности (активная мощность) генератора будет равно сумме активных мощностей отдельных фаз
где U, I – действующие напряжения и ток в фазах, φ – угол между напряжением и током в фазах.
Слайд 52
Мощность трехфазной цепи.
Активная мощность
Активная мощность приемников трехфазной цепи равна сумме активных
при соединении потребителей треугольником:
При симметричной нагрузке, т.е. когда
или
Слайд 54
Мощность трехфазной цепи.
Реактивная мощность
Реактивная мощность трехфазной цепи равна сумме реактивных мощностей
где U, I – действующие напряжения и ток в фазах, φ – угол между напряжением и током в фазах.
При симметричной нагрузке, т.е. когда
Слайд 55
Мощность трехфазной цепи.
Реактивная мощность
т.к. при соединении нагрузки звездой напряжение:
, а
то мощность можно записать через линейные напряжения и токи
такое же выражение получится для соединения нагрузки по схеме треугольник.
Слайд 56
Мощность трехфазной цепи.
Полная мощность
Полная мощность трехфазной цепи определяется выражением:
Поэтому полную мощность
При симметричной нагрузке полная мощность определяется
Слайд 57
Задача 8.3.
Как изменится активная мощность, если трехфазный симметричный резистивный приемник, соединенный
Решение:
Допустим сопротивление приемников 1 Ом, а линейное напряжение равно 1 В
тогда мощность нагрузки сети при соединении в звезду:
, Вт
При соединении треугольником линейное напряжение равно фазному:
тогда мощность нагрузки
, Вт
т.е. при соединении треугольником мощность нагрузки больше в 3 раза по сравнению с соединением звезда при одном и том же сопротивлении фаз.
Слайд 58Коэффициент мощности трехфазных симметричных приемников.
Значительную часть приемников электрической энергии составляют трехфазные
Большая часть промышленных приемников потребляет из сети помимо активной реактивную энергию. Основными потребителями реактивной энергии являются асинхронные двигатели и трансформаторы, потребляющие соответственно 60—65 и 20 – 25% общего количества реактивной энергии
Слайд 59Коэффициент мощности трехфазных симметричных приемников.
При загрузке линий электропередач и трансформаторов значительными
Поэтому в современных системах электроснабжения стремятся частично разгружать линии электропередач и трансформаторы от реактивной энергии, приближая в соответствии с технико-экономическими возможностями источники реактивной энергии к местам ее потребления. Это приводит к повышению коэффициента мощности установок.
Слайд 60Коэффициент мощности трехфазных симметричных приемников.
Улучшение коэффициента мощности промышленных предприятий осуществляться прежде
В случае необходимости прибегают к искусственным мерам повышения коэффициента мощности с помощью компенсирующих устройств (источников реактивной энергии) — синхронных компенсаторов (синхронных двигателей), работающих в специальном режиме, и статических конденсаторов.
Слайд 61Коэффициент мощности трехфазных симметричных приемников.
Коэффициент мощности трехфазных приемников
где QC –
Чем больше реактивная энергия, вырабатываемая компенсирующими устройствами, установленными вблизи приемников, тем выше коэффициент мощности.
Выбор компенсирующих устройств осуществляют на основе технико-экономических расчетов. Применение синхронных компенсаторов в маломощных установках нерационально, поэтому на промышленных предприятиях при мощности компенсирующего устройства менее 5 Мвар (при U = 6 кВ) и 10 Мвар (при U = 10 кВ) экономически целесообразна установка конденсаторных батарей.
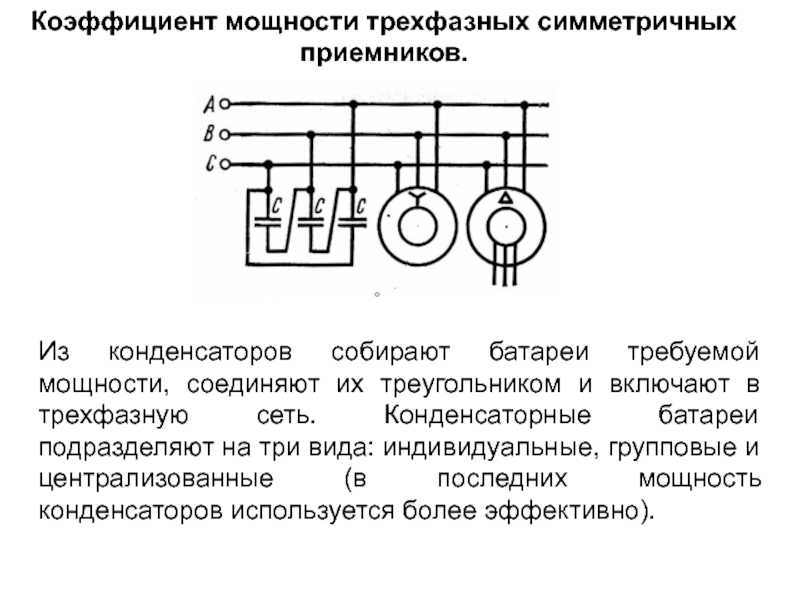
Слайд 62Коэффициент мощности трехфазных симметричных приемников.
Из конденсаторов собирают батареи требуемой мощности, соединяют
Слайд 63Техника безопасности при эксплуатации трехфазных цепей
При эксплуатации трехфазных цепей должны быть
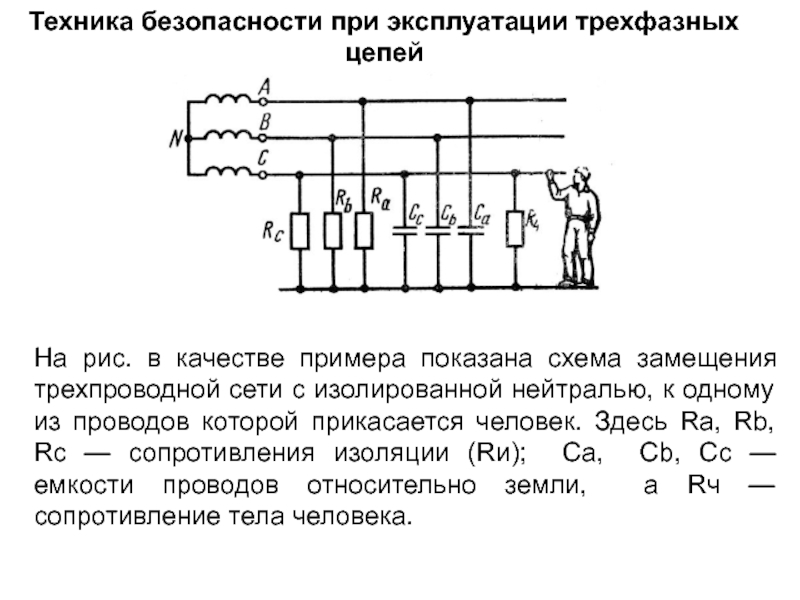
Электрический ток, проходя через тело человека, производит термическое, электрическое и биологическое воздействия. Опасность поражения током зависит от его значения, продолжительности действия и ряда других факторов. Токи промышленной частоты порядка 0,01-0,015 А опасны для жизни, а токи, превышающие 0,1 А - смертельны.
Слайд 64Техника безопасности при эксплуатации трехфазных цепей
Человек может оказаться под напряжением при
В трехфазных сетях низкого напряжения (до 1000 В) значение тока, поражающего человека, зависит от «режима нейтрали» (т. е. заземлена или изолирована нейтральная точка источника электрической энергии), а также от активной и реактивной проводимостей, существующих между проводами и землей.
Слайд 65Техника безопасности при эксплуатации трехфазных цепей
На рис. в качестве примера показана
Слайд 66Техника безопасности при эксплуатации трехфазных цепей
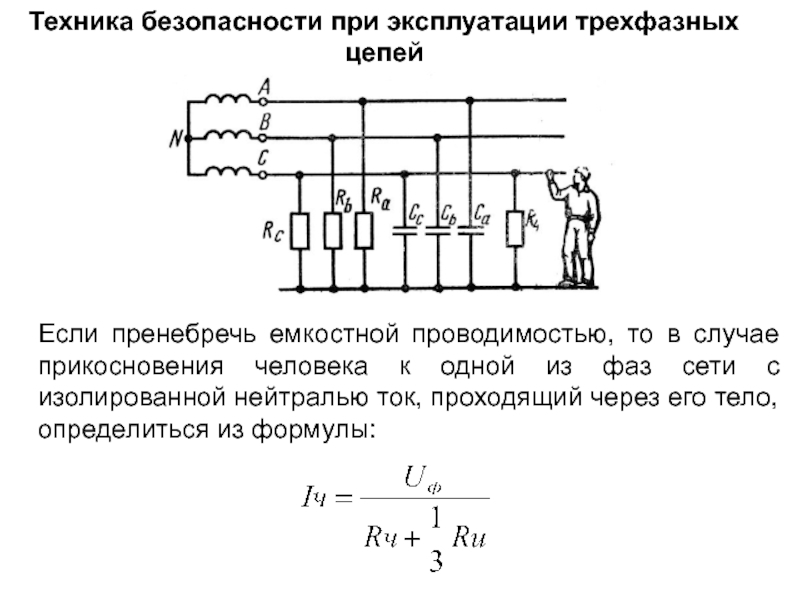
Если пренебречь емкостной проводимостью, то в
Слайд 67Техника безопасности при эксплуатации трехфазных цепей
Из формулы следует, что чем хуже
Слайд 68Техника безопасности при эксплуатации трехфазных цепей
Для снижения напряжения, прикосновения к металлическим
Слайд 69Техника безопасности при эксплуатации трехфазных цепей
В четырехпроводных сетях с заземленной нейтралью
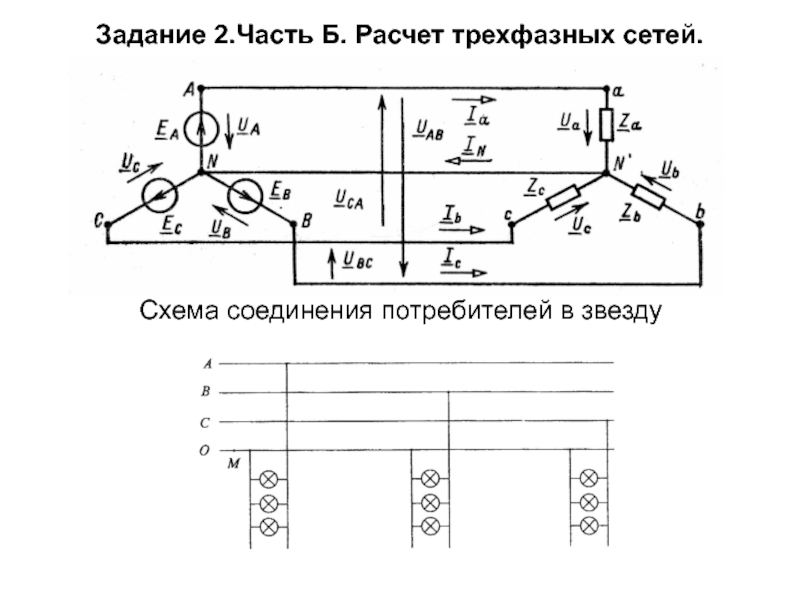
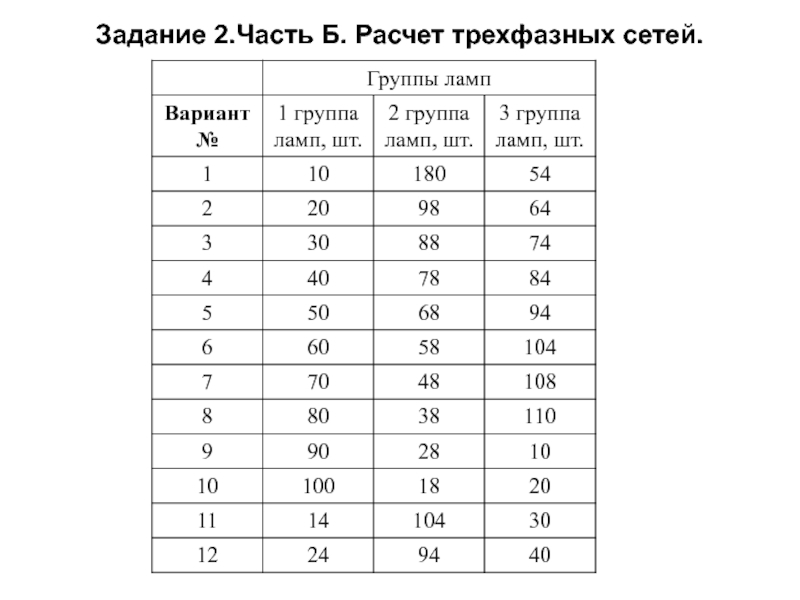
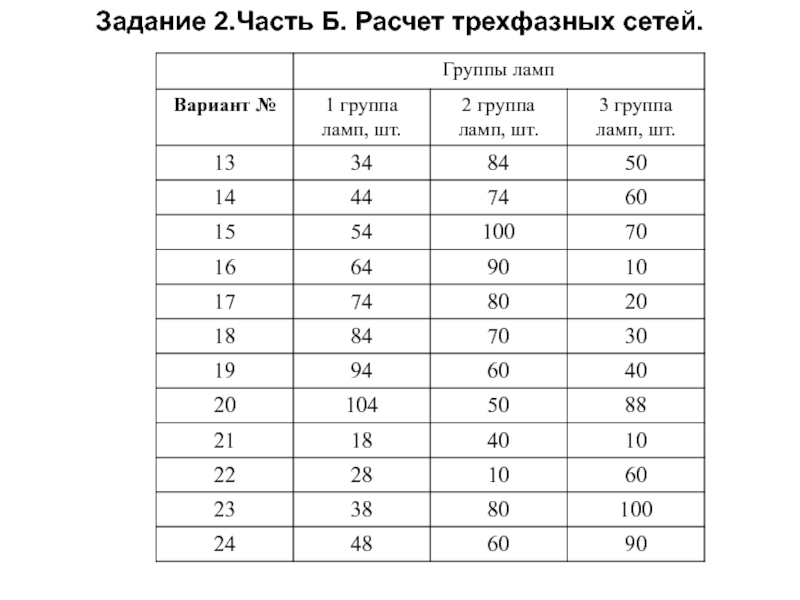
Слайд 70Задание 2.Часть Б. Расчет трехфазных сетей.
Вариант (данные групп ламп из таблицы
Для заданной цепи:
При соединении потребителей в звезду:
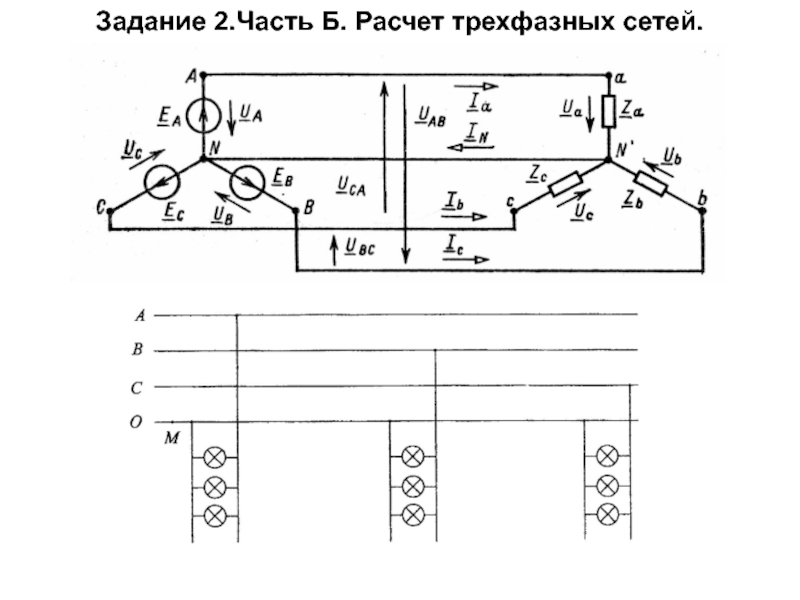
Условие: в четырехпроводную линию трехфазной симметричной сети с фазным напряжением Uф=UA=UB=UC=220 В включены группы ламп (все лампы одинаковые, включены параллельно, сопротивление одной лампы R= 400, Ом) по схеме звезда. Первая группа ламп соединяется к фазе А (сопротивление в фазе - Za), вторая группа к фазе В (сопротивление в фазе - Zb) и третья группа к фазе С (сопротивление в фазе - Zc)
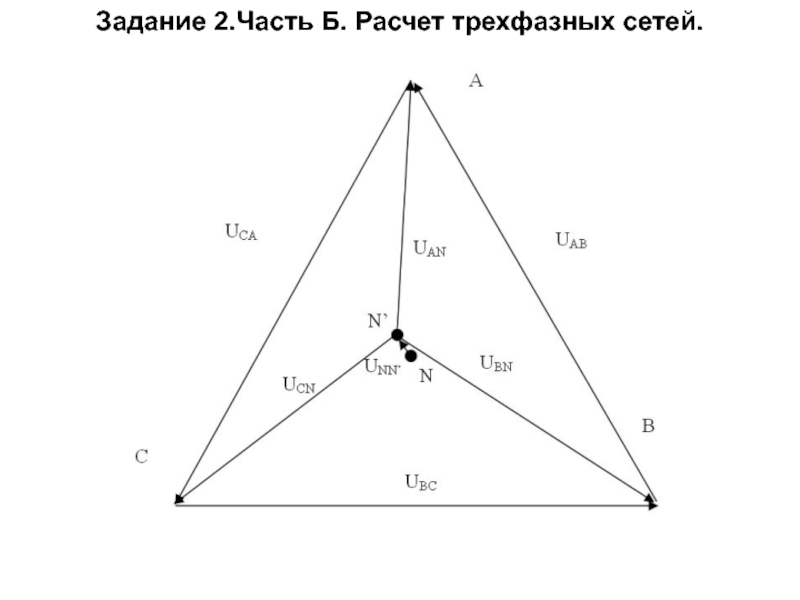
Слайд 72Задание 2.Часть Б. Расчет трехфазных сетей.
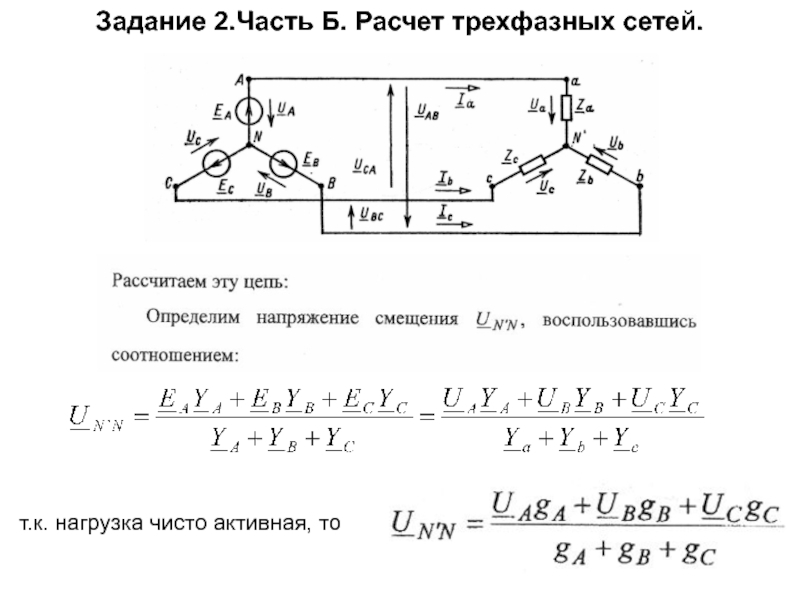
определить напряжение смещение нейтрали.
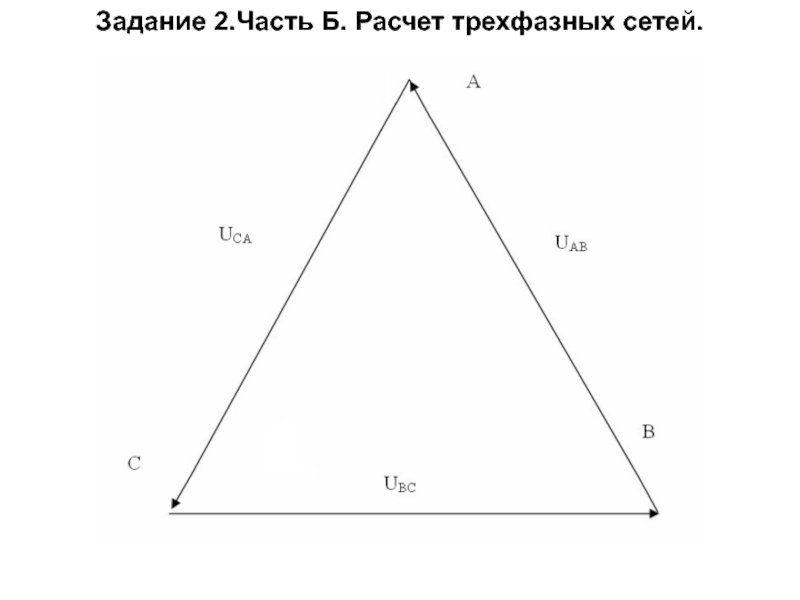
определить линейные напряжения.
определить
определить ток в нейтральном проводе.
рассчитать мощность трехфазной сети
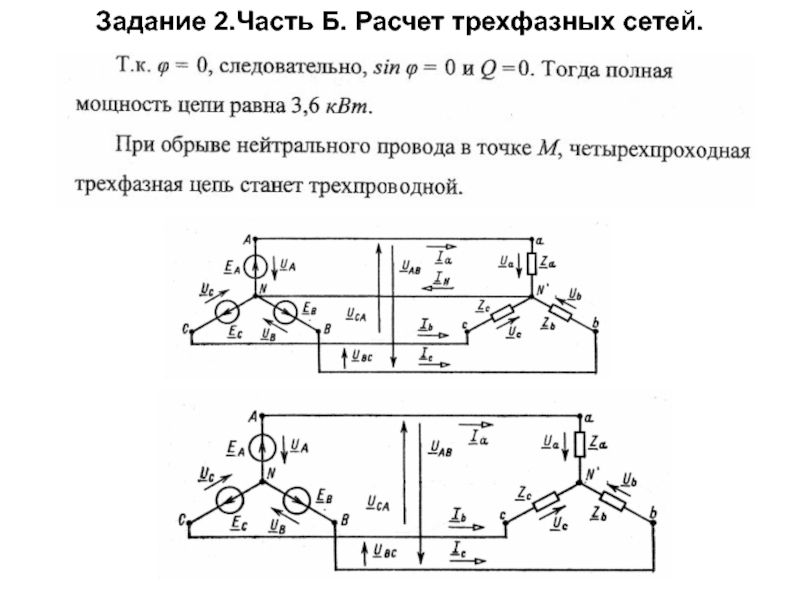
под каким напряжением окажется нагрузка в каждой фазе при обрыве нейтрального провода в точке М.
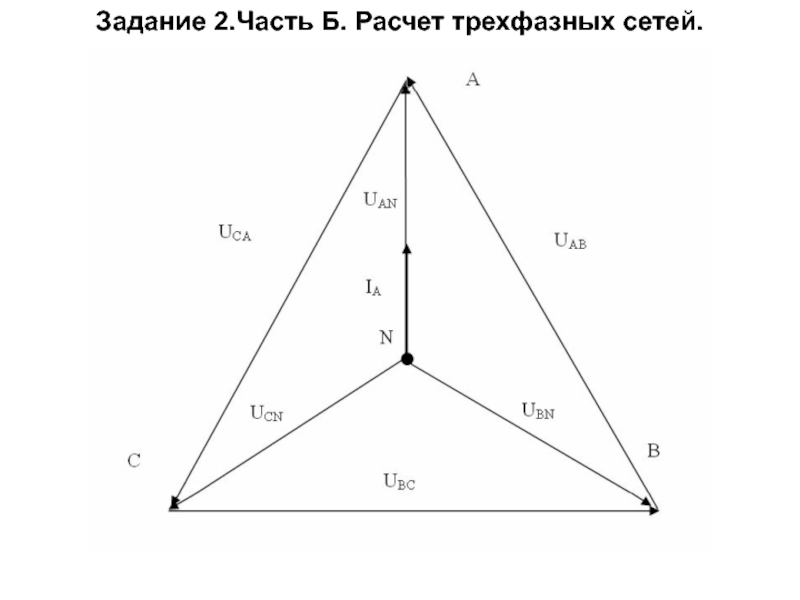
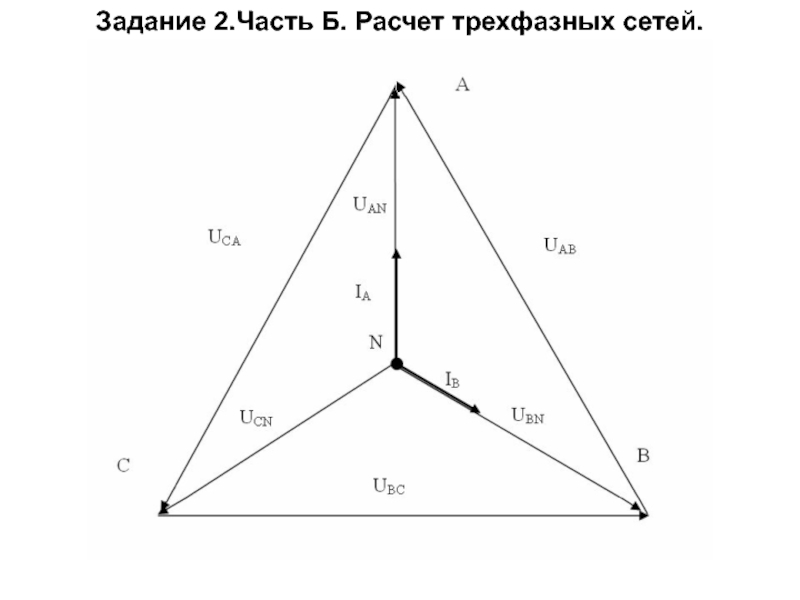
построить векторные диаграммы токов и напряжений на комплексной плоскости, направив напряжение фазы А по действительной оси
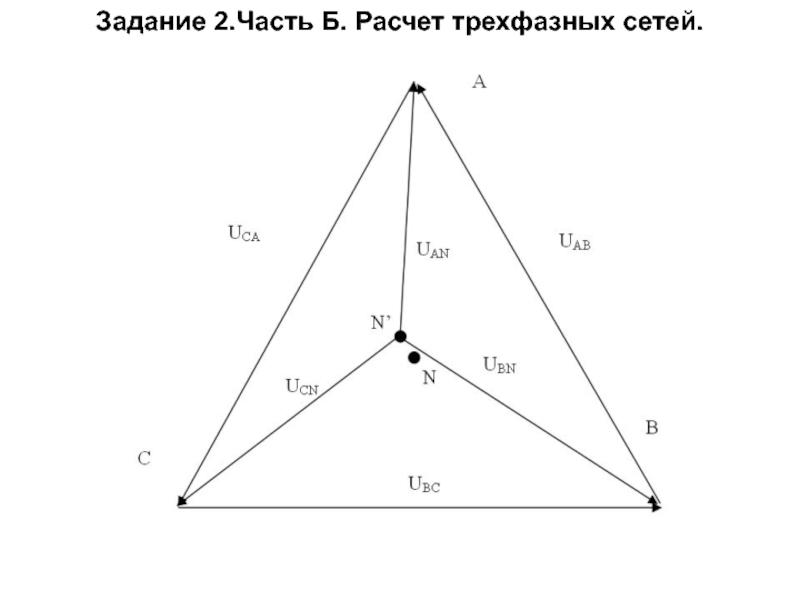
Слайд 73Задание 2.Часть Б. Расчет трехфазных сетей.
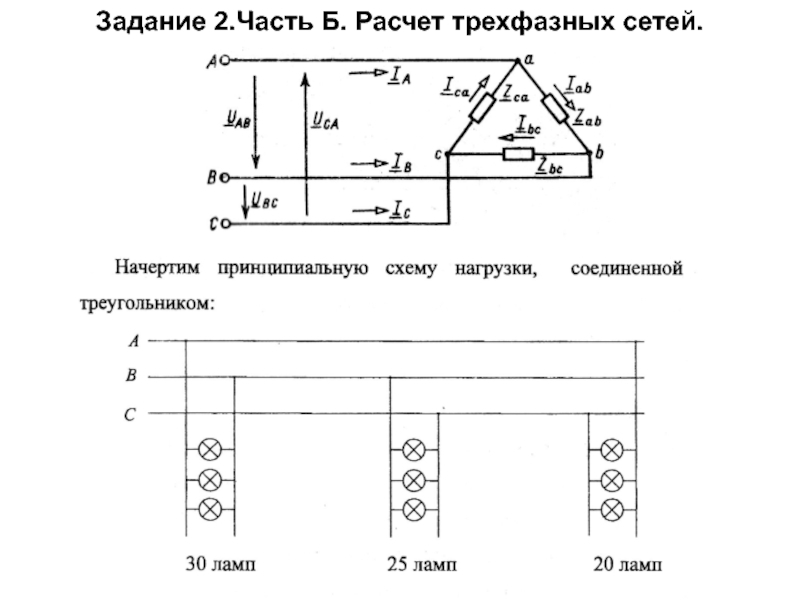
При соединении потребителей в треугольник
Условие: в
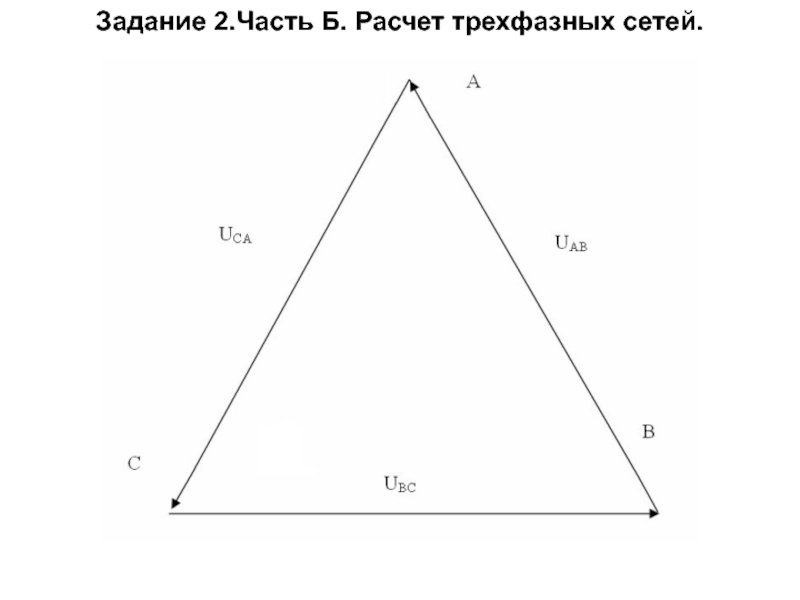
Слайд 74Задание 2.Часть Б. Расчет трехфазных сетей.
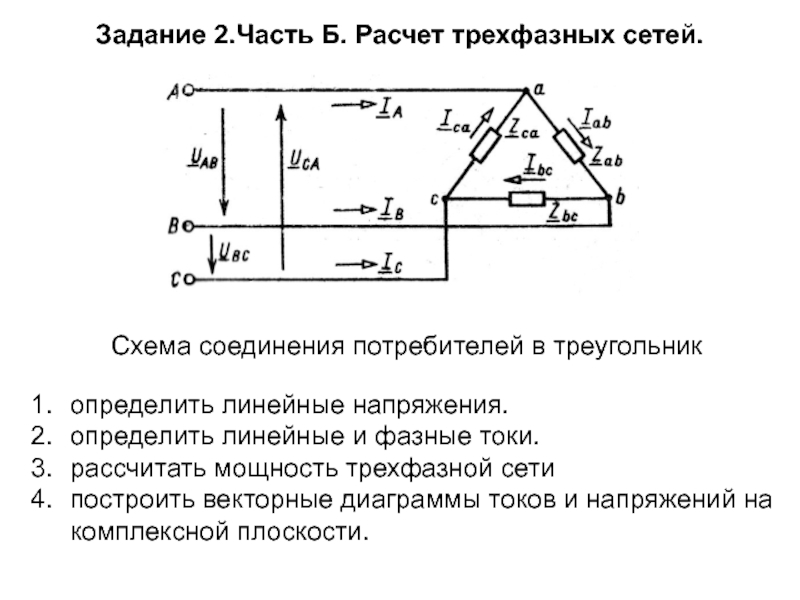
определить линейные напряжения.
определить линейные и фазные
рассчитать мощность трехфазной сети
построить векторные диаграммы токов и напряжений на комплексной плоскости.
Схема соединения потребителей в треугольник