- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Строительная механика. Методы определения силовых факторов в деформируемых системах презентация
Содержание
- 1. Строительная механика. Методы определения силовых факторов в деформируемых системах
- 2. Силовые факторы – реакции связей внешних
- 3. Силовые факторы – реакции связей внешних
- 4. Силовые факторы – реакции связей внешних
- 5. Силовые факторы – реакции связей внешних
- 6. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
- 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
- 8. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
- 9. Возможные (виртуальные) перемещения – а)
- 10. q F1
- 11. Алгоритм определения реакции связи кинематическим методом 1.
- 12. Алгоритм определения реакции связи кинематическим методом 1.
- 14. B
- 15. B
- 16. Удаление внутренних связей . Смысл перемещения δS
- 17. Удаление внутренних связей . Смысл перемещения δS
- 18. Удаление внутренних связей . Смысл перемещения δS
- 19. Удаление внутренних связей . Смысл перемещения δS
- 20. Удаление внутренних связей . Смысл перемещения δS
- 21. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
- 22. К о н т р о л
- 23. К о н т р о л
Слайд 1МЕТОДЫ ОПРЕДЕЛЕНИЯ СИЛОВЫХ ФАКТОРОВ
В ДЕФОРМИРУЕМЫХ СИСТЕМАХ
С
ВГ
СТРОИТЕЛЬНАЯ МЕХАНИКА.
Часть I
Слайд 2
Силовые факторы – реакции связей
внешних (опорные реакции)
внутренних
в сечениях элементов
(внутренние силовые факторы)
Методы определения
силовых факторов
статический
кинематический
энергетический
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
Сущность статического метода – непосредственное использование уравнений равновесия системы в целом и/или её частей.
Уравнения равновесия в случае линейно деформируемой системы:
A*S + BF = 0
дифференциальные уравнения
для бесконечно малого элемента
линейные алгебраические уравнения
для системы элементов конечных размеров ( дискретной системы )
S – вектор искомых усилий;
А – матрица коэффициентов
при неизвестных S
в уравнениях равновесия;
ВF – вектор «грузовых» членов
уравнений равновесия
(от заданных нагрузок).
Для системы в целом:
– число искомых усилий nS = nc ;
– количество уравнений nyp= nΔ .
В случае статически определимой
cистемы (W = 0) nΔ=nc nyp= nS
F1
F2
q
M
h
l
l/2
l/2
F1
q
F2
q
A
A
B
B
C
C
C
HA
VA
MA
VC
VC
HC
VB
nΔ= 3*2 = 6 = nyp ;
nc = nS = 6
Вектор искомых
реакций связей:
M
h
l
l/2
l/2
Слайд 3
Силовые факторы – реакции связей
внешних (опорные реакции)
внутренних
в сечениях элементов
(внутренние силовые факторы)
Методы определения
силовых факторов
статический
кинематический
энергетический
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
Сущность статического метода – непосредственное использование уравнений равновесия системы в целом и/или её частей.
A*S + BF = 0
дифференциальные уравнения
для бесконечно малого элемента
линейные алгебраические уравнения
для системы элементов конечных размеров ( дискретной системы )
S – вектор искомых усилий;
А – матрица коэффициентов
при неизвестных S
в уравнениях равновесия;
ВF – вектор «грузовых» членов
уравнений равновесия
(от заданных нагрузок).
Для системы в целом:
– число искомых усилий nS = nc ;
– количество уравнений nyp= nΔ .
В случае статически определимой
cистемы (W = 0) nΔ=nc nyp= nS
F1
q
F2
q
A
B
C
C
HA
MA
VC
VC
HC
VB
Вектор искомых
реакций связей:
l
l/2
l/2
Уравнения
равновесия:
h
Уравнения равновесия:
nΔ= 3*2 = 6 = nyp ;
nc = nS = 6
M
VA
Уравнения равновесия в случае линейно деформируемой системы:
Слайд 4
Силовые факторы – реакции связей
внешних (опорные реакции)
внутренних
в сечениях элементов
(внутренние силовые факторы)
Методы определения
силовых факторов
статический
кинематический
энергетический
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
Сущность статического метода – непосредственное использование уравнений равновесия системы в целом и/или её частей.
A*S + BF = 0
дифференциальные уравнения
для бесконечно малого элемента
линейные алгебраические уравнения
для системы элементов конечных размеров ( дискретной системы )
S – вектор искомых усилий;
А – матрица коэффициентов
при неизвестных S
в уравнениях равновесия;
ВF – вектор «грузовых» членов
уравнений равновесия
(от заданных нагрузок).
Для системы в целом:
– число искомых усилий nS = nc ;
– количество уравнений nyp= nΔ .
В случае статически определимой
cистемы (W = 0) nΔ=nc nyp= nS
F1
q
F2
q
A
B
C
C
HA
MA
VC
VC
HC
VB
Вектор искомых
реакций связей:
l
l/2
l/2
Уравнения равновесия:
h
nΔ= 3*2 = 6 = nyp ;
nc = nS = 6
M
VA
Уравнения равновесия в случае линейно деформируемой системы:
необходимое и достаточное
статическое условие
геометрической неизменяемости
системы
Слайд 5
Силовые факторы – реакции связей
внешних (опорные реакции)
внутренних
в сечениях элементов
(внутренние силовые факторы)
Методы определения
силовых факторов
статический
кинематический
энергетический
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
Сущность статического метода – непосредственное использование уравнений равновесия системы в целом и/или её частей.
A*S + BF = 0
линейные алгебраические уравнения
для системы элементов конечных размеров ( дискретной системы )
S – вектор искомых усилий;
А – матрица коэффициентов
при неизвестных S
в уравнениях равновесия;
ВF – вектор «грузовых» членов
уравнений равновесия
(от заданных нагрузок).
Уравнения равновесия в случае линейно деформируемой системы:
Универсальная процедура формирования
системы уравнений равновесия
( концепция конечных элементов )
1. Разделение системы на элементы и узлы
сечениями по концам стержневых элементов
( концевыми сечениями ).
2. Запись уравнений:
– 1-я группа – уравнения равновесия элементов в локальных (собственных) осях координат – стандартная процедура;
– 2-я группа – уравнения равновесия узлов
( включая опорные ) в общей ( глобальной )
системе координат;
– 3-я группа – статические характеристики
связей в узлах.
Слайд 6
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
A*S + BF = 0
системы уравнений равновесия
( концепция конечных элементов )
1. Разделение системы на элементы и узлы
сечениями по концам стержневых элементов
( концевыми сечениями ).
2. Запись уравнений:
– 1-я группа – уравнения равновесия элементов в локальных (собственных) осях координат – стандартная процедура;
– 2-я группа – уравнения равновесия узлов
( включая опорные ) в общей ( глобальной )
системе координат;
– 3-я группа – статические характеристики
связей в узлах.
П р и м е р
q
F
l
l /2
a
a
1
2
3
4
1
2
3
4
b1
b2
b3
b4
e2
e3
e1
2
3
1
F
F
2
3
4
q
q
А
В
1
4
HA
VA
MA
HB
VB
MB
Mb1
Nb1
Qb1
Qb1
Me1
Ne1
Qe1
Qe1
Mb2
Qb2
Nb2
Me2
Qe2
Ne2
Qe2
Nb4
Mb4
Qb4
Qb4
Qb3
Qe3
Qe3
Ne3
Me3
Mb3
Qb3
Nb3
Вектор
искомых
усилий
Усилия в концевых сечениях
элементов (21)
Реакции опор
(6)
У р а в н е н и я 1-й г р у п п ы:
j
q
Qbj
Qej
Nej
Nbj
Mbj
Mej
bj
ej
lj
xj
yj
от нагрузки
j = 1, 2, 3, 4
Количество
уравнений
1-й группы – 12
У р а в н е н и я 2-й г р у п п ы:
2
F
Me1
Qe1
Ne1
Nb2
Qb2
Mb2
x
y
1
HA
VA
MA
Mb1
Nb1
Qb1
t = 1, 2, 3, 4
Количество
уравнений
2-й группы – 12
У равнения
3-й группы
( 3 ):
MA = 0
HB = 0
Me2 = 0
Общее
число
уравнений
27
nyp= nS
Слайд 7
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
СТАТИЧЕСКИМ МЕТОДОМ
В случае статически неопределимой системы
W < 0
nΔ< nc
nyp< nS
Недостающие уравнения в количестве nc – nΔ = nл.с. – геометрические:
AD* Δ + D = 0 – условия совместности перемещений
(например, описание перемещений по направлениям лишних связей)
Объединённая система уравнений:
A* S + BF = 0
AD* Δ + D = 0
Из физических зависимостей ( закон Гука и др. ):
Δ = Δ (S) – выражения перемещений через усилия
Разрешающие уравнения в усилиях: A0* S + B0 = 0
Необходимое и достаточное аналитическое условие
геометрической неизменяемости системы:
Слайд 8
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ
(СИЛОВЫХ ФАКТОРОВ)
КИНЕМАТИЧЕСКИМ МЕТОДОМ
В основе метода – принцип
если механическая система находится в равновесии,
то сумма работ внешних сил, приложенных к системе,
и соответствующих им внутренних сил
на возможных ( виртуальных ) перемещениях
равна нулю:
Wext + Wint = 0
*J.L. Lagrange ( 1788 )
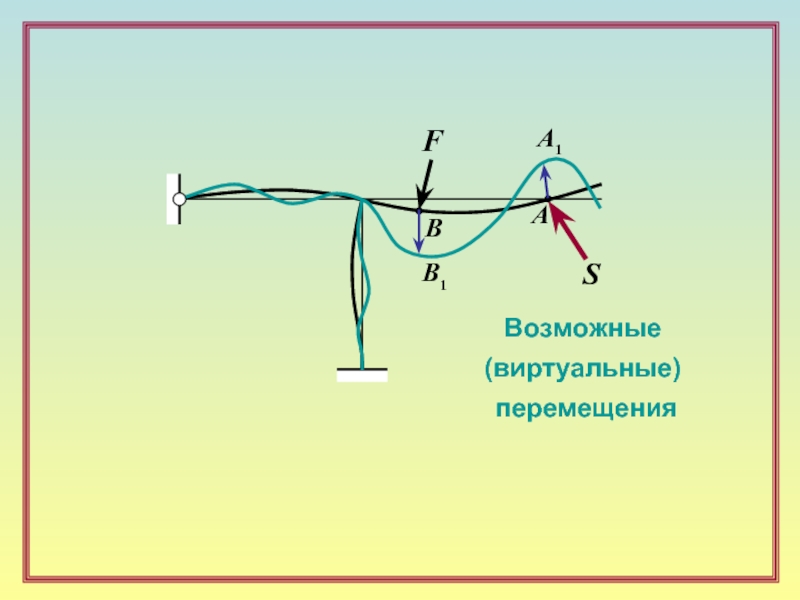
Слайд 9Возможные (виртуальные)
перемещения –
а) бесконечно малые ( для линейно
но малые в сравнении с габаритами
системы );
б) не противоречащие условиям
совместности деформаций
( перемещений ) и кинематическим
граничным условиям ( условиям
закрепления );
в) отсчитываемые от исследуемого
положения равновесия.
Слайд 10
q
F1
Fn
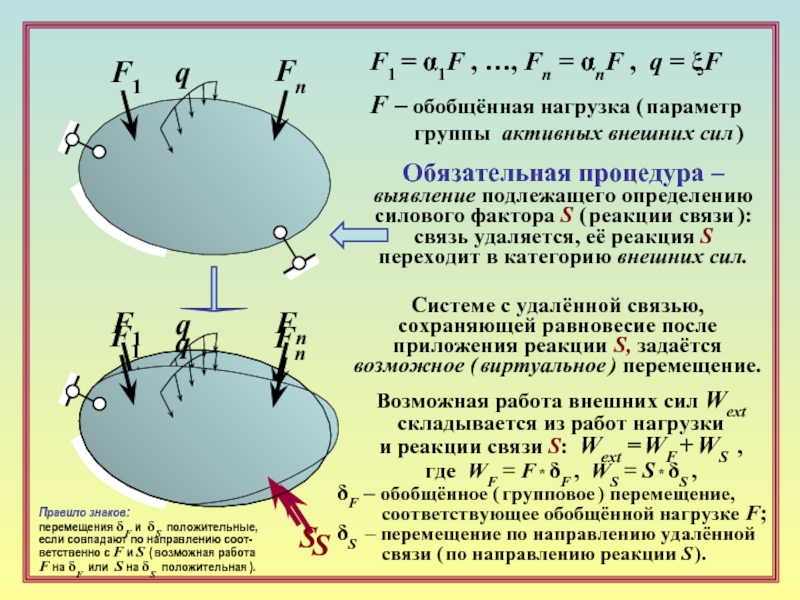
F1 = α1F , …, Fn = αnF , q =
F – обобщённая нагрузка ( параметр
группы активных внешних сил )
q
F1
S
Fn
Fn
F1
q
S
Обязательная процедура –
выявление подлежащего определению
силового фактора S ( реакции связи ):
cвязь удаляется, её реакция S переходит в категорию внешних сил.
Системе с удалённой связью, сохраняющей равновесие после приложения реакции S, задаётся возможное ( виртуальное ) перемещение.
Возможная работа внешних сил Wext
складывается из работ нагрузки
и реакции связи S: Wext = WF + WS ,
где WF = F * δF , WS = S * δS ,
δF – обобщённое ( групповое ) перемещение,
соответствующее обобщённой нагрузке F;
δS – перемещение по направлению удалённой
связи ( по направлению реакции S ).
Правило знаков:
перемещения δF и δS положительные, если совпадают по направлению соот-ветственно с F и S ( возможная работа
F на δF или S на δS положительная ).
Слайд 11Алгоритм
определения реакции связи
кинематическим методом
1. В системе, находящейся в равновесном деформированном
которой S требуется определить. Взамен удалённой связи
прикладывается её реакция S, обеспечивающая сохранение
неизменным состояния равновесия системы.
2. Системе с удалённой связью, находящейся по-прежнему
в равновесном деформированном состоянии при действующей
нагрузке и реакции S, задаётся возможное (виртуальное)
перемещение.
3. Определяются (с точностью до общего неопределённого
множителя δ0 ) перемещения δF и δS – соответственно
по направлениям заданной нагрузки F и искомой реакции S.
4. Из уравнения возможных работ Wext + Wint = 0 определяется
искомый силовой фактор S (реакция связи):
Слайд 12Алгоритм
определения реакции связи
кинематическим методом
1. В системе, находящейся в равновесном деформированном
которой S требуется определить. Взамен удалённой связи
прикладывается её реакция S, обеспечивающая сохранение
неизменным состояния равновесия системы.
2. Системе с удалённой связью, находящейся по-прежнему
в равновесном деформированном состоянии при действующей
нагрузке и реакции S, задаётся возможное (виртуальное)
перемещение.
3. Определяются (с точностью до общего неопределённого
множителя δ0 ) перемещения δF и δS – соответственно
по направлениям заданной нагрузки F и искомой реакции S.
4. Из уравнения возможных работ Wext + Wint = 0 определяется
искомый силовой фактор S (реакция связи):
Слайд 13
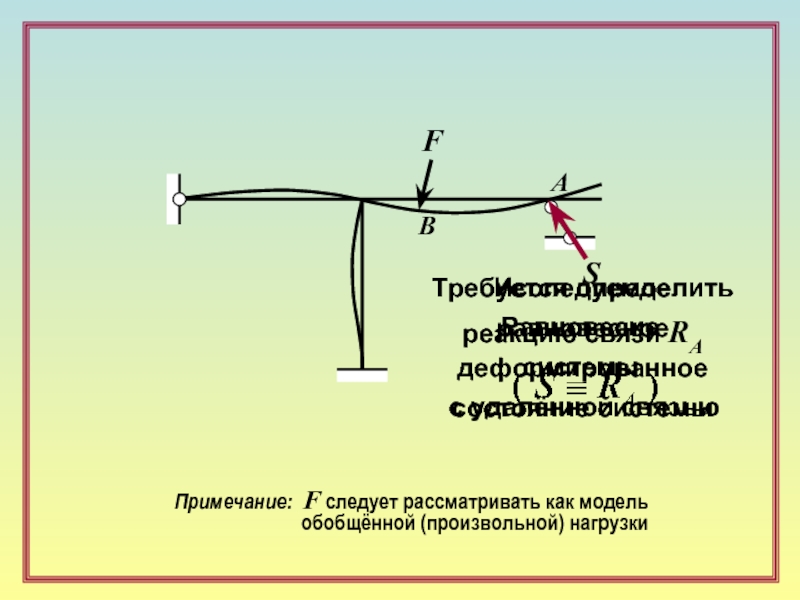
А
Требуется определить
реакцию связи RA
B
F
Исследуемое
равновесное
деформированное
состояние системы
S
Равновесие
системы
с удалённой связью
Примечание: F следует рассматривать
обобщённой (произвольной) нагрузки
Слайд 15
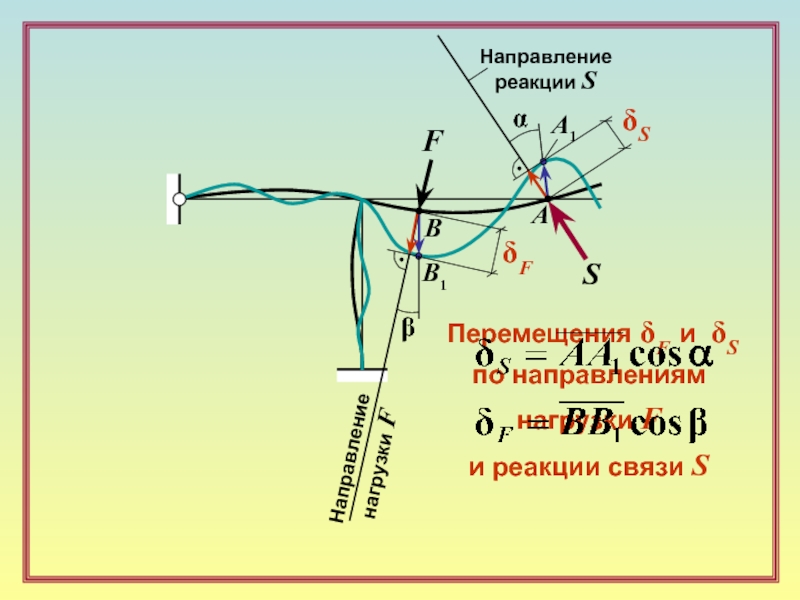
B
F
А
S
Перемещения δF и δS
по направлениям
нагрузки F
и реакции связи S
B1
A1
Направление
нагрузки
Направление
реакции S
β
α
δS
δF
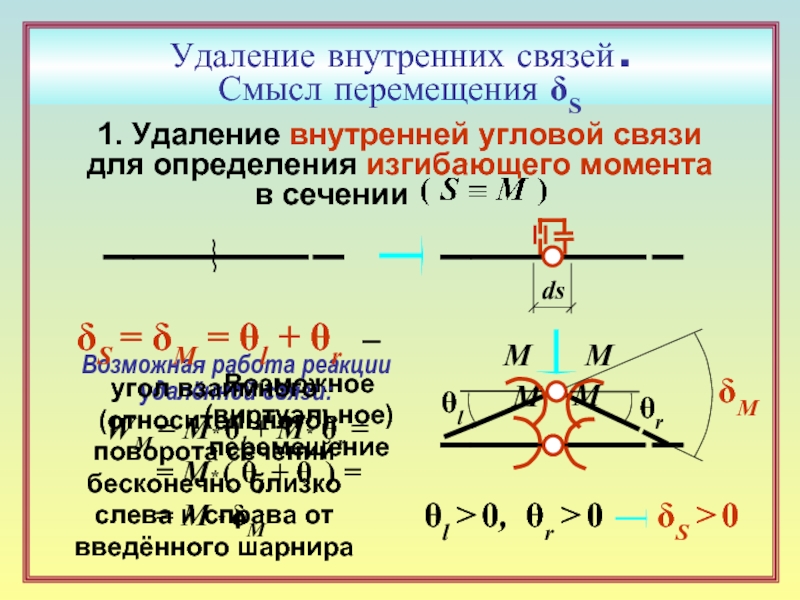
Слайд 16Удаление внутренних связей .
Смысл перемещения δS
1. Удаление внутренней угловой связи
для определения
в сечении
ds
M
M
M
M
Возможное (виртуальное) перемещение
Возможная работа реакции
удалённой связи:
WM = M* θl + M* θr =
= M* ( θl + θr ) =
= M * δM
θl
θr
δM
δS = δM = θl + θr –
угол взаимного (относительного) поворота сечений бесконечно близко слева и справа от введённого шарнира
θl > 0, θr > 0 δS > 0
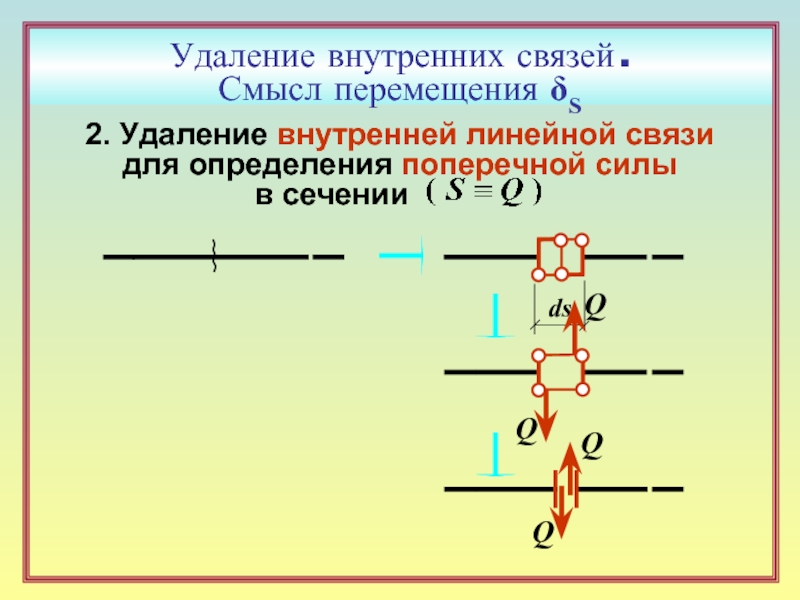
Слайд 17Удаление внутренних связей .
Смысл перемещения δS
2. Удаление внутренней линейной связи
для определения
в сечении
ds
Q
Q
Q
Q
Слайд 18Удаление внутренних связей .
Смысл перемещения δS
2. Удаление внутренней линейной связи
для определения
в сечении
Q
Q
Возможное (виртуальное) перемещение
Параллельно
δl
δr
a1
b1
a
b
Возможная работа реакции
удалённой связи:
WQ = Q* δl + Q* δr =
= Q* ( δl + δr ) =
= Q * δQ
δS = δQ = δl + δr –
взаимное (относительное) нормальное к оси стержня линейное перемещение сечений ( точек a и b ) бесконечно близко
слева и справа от введённого поступательного шарнира
δl > 0, δr > 0 δS > 0
δQ
δS = δQ
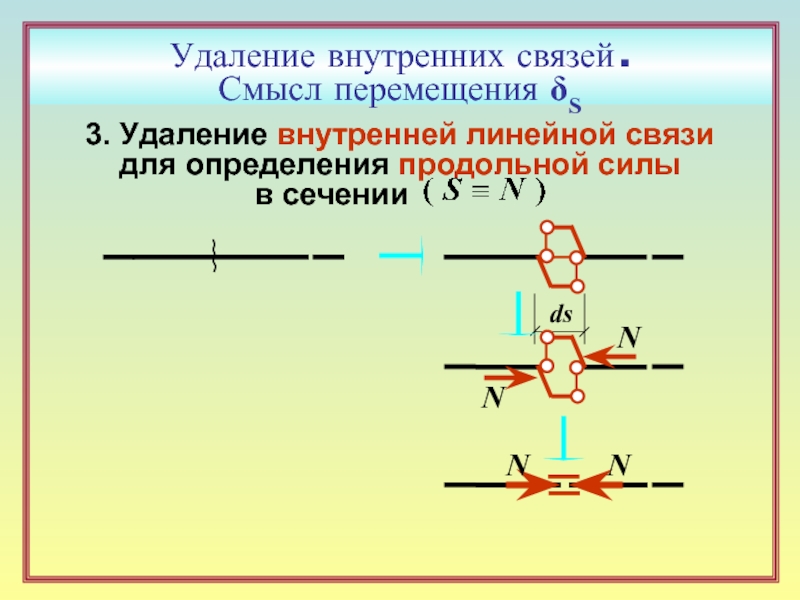
Слайд 19Удаление внутренних связей .
Смысл перемещения δS
3. Удаление внутренней линейной связи
для определения
в сечении
ds
N
N
N
N
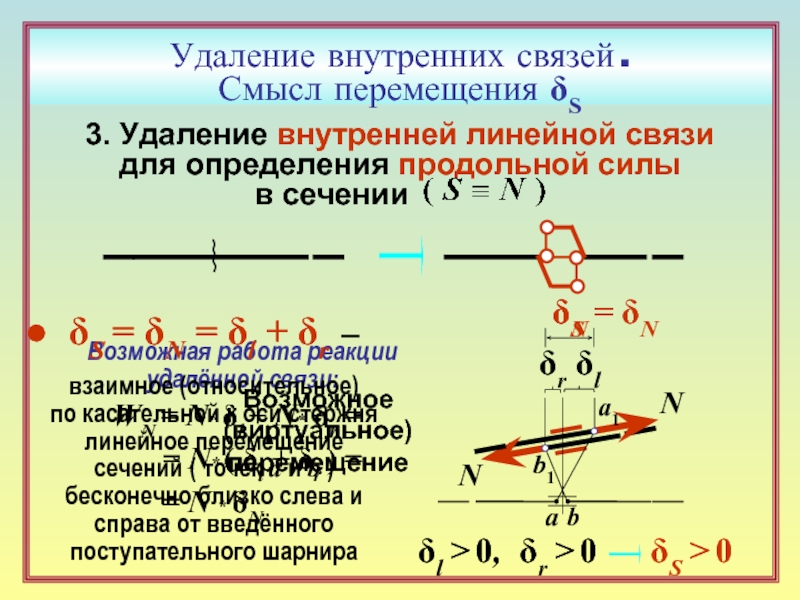
Слайд 20Удаление внутренних связей .
Смысл перемещения δS
3. Удаление внутренней линейной связи
для определения
в сечении
N
N
δr
δl
Возможное (виртуальное) перемещение
a
a1
b
b1
Возможная работа реакции
удалённой связи:
WN = N* δl + N* δr =
= N* ( δl + δr ) =
= N * δN
δS = δN = δl + δr –
взаимное (относительное)
по касательной к оси стержня линейное перемещение сечений ( точек a и b ) бесконечно близко слева и справа от введённого поступательного шарнира
δN
δS = δN
δl > 0, δr > 0 δS > 0
Слайд 21
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ (СИЛОВЫХ ФАКТОРОВ)
ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
Силовой фактор S в линейно
( т е о р е м а Л а г р а н ж а ):
Слайд 22К о н т р о л ь н ы е
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 22» )
1. Какие силовые факторы определяются в расчётах сооружений и конструкций? ( 2 )
2. Перечислить основные методы определения силовых факторов. ( 2 )
3. В чём сущность статического метода определения реакций связей и внутренних
усилий? ( 2 )
4. Какими уравнениями описывается равновесие
а) дифференциально-малого элемента ( 2 )
б) дискретной ( конечно-элементной ) линейно деформируемой системы? ( 2 )
5. Каково соотношение между числом уравнений равновесия и количеством искомых
силовых факторов в случае статически определимой системы? ( 2 )
6. В чём суть универсальной процедуры формирования уравнений равновесия,
реализующей концепцию конечных элементов? ( 5 )
7. Из каких групп состоит система уравнений равновесия, формируемых с помощью
универсальной процедуры? ( 4 ) универсальной процедуры? ( 4 ) ( 6 )
8. Какие особенности имеет применение статического метода к статически
неопределимым системам? ( 7 )
9. Каково необходимое и достаточное аналитическое ( статическое ) условие
геометрической неизменяемости системы? ( 4 ) геометрической неизменяемости системы? ( 4 ) ( 7 )
10. На чём основан кинематический метод определения реакций связей ( силовых
факторов )? Дать формулировку принципа Лагранжа. ( 8 )
11. Что такое возможные ( виртуальные ) перемещения? – три их свойства. ( 9 )
12. Какая обязательная процедура предшествует заданию виртуальных перемещений
при реализации кинематического метода определения реакции некоторой связи? ( 10 )
13. Что такое обобщённая нагрузка и обобщённое перемещение? ( 10 )
_____________________________________________________
*) Только в режиме «Показ слайдов»
Слайд 23К о н т р о л ь н ы е
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 23» )
14. Изложить алгоритм определения реакции связи кинематическим методом. ( 11 )
15. Основная формула кинематического метода для определения
силового фактора S . ( 11 )
16. Что такое δF и δS в основной формуле кинематического метода? ( 10 )
17. Каково правило знаков для перемещений δF и δS? ( 10 )
18. Какие связи должны удаляться при определении внутренних силовых факторов кинематическим методом? ( самостоятельно )
19. Какая связь удаляется при определении кинематическим методом изгибающего
момента в определённом сечении стержневого элемента? Что появляется в сечении
в результате удаления связи? ( 16 )
20. Какой смысл имеет величина δS в случае определения изгибающего момента М ? ( 16 )
21. Какая связь удаляется при определении кинематическим методом поперечной силы
в сечении стержневого элемента? Что появляется в сечении в результате удаления связи? ( 17 )
22. Какой смысл имеет величина δS в случае определения поперечной силы Q ? ( 18 )
23. Какая связь удаляется при определении кинематическим методом продольной силы
в сечении стержневого элемента? Что появляется в сечении в результате удаления связи? ( 19 )
24. Какой смысл имеет величина δS в случае определения продольной силы N ? ( 20 )
25. На чём основан энергетический метод определения силовых факторов
в деформируемых системах? ( 21 )
26. Аналитическая запись энергетической теоремы Лагранжа для определения силового
фактора S . ( 21)
_____________________________________________________
*) Только в режиме «Показ слайдов»