- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дисперсиялык талдаудын бір факторлы параметрлік емес үқсастығы критерий - Крускал Уоллис критерийі презентация
Содержание
- 1. Дисперсиялык талдаудын бір факторлы параметрлік емес үқсастығы критерий - Крускал Уоллис критерийі
- 2. Жоспары: І. Кіріспе ІІ. Негізгі бөлім
- 3. Дисперсия бұл әртүрлі факторлардың әсерінен туындайтын белгінің
- 4. Дисперсиялық талдау міндеттері: белгіленген немесе кездейсоқ болулары
- 5. Эксперименттік ұйғарымдарда дисперсиялық талдаудың бірнеше
- 6. Бір факторлы дисперсиялық талдау Мысалы: фактор -
- 7. Дисперсиялық талдаудың негізгі идеясы: Таңдама дисперсияны екі
- 8. Топтық орта мәндердің теңдігі жөніндегі нөлдік жорамалда
- 9. Факторлық дисперсия: Мұндағы
- 10. Қалдық дисперсияны есептеу формуласы мұндағы
- 11. Бірфакторлық дисперсиялық талдау Дисперсиялық талдауды жүргізу әдісі:
- 12. 3. Есептеледі MSфактжәне MSкалд Егер
- 14. Краскел-Уоллиса критерийі бірнеше таңдамалылардың медиандарын тексеруге арналған.
- 15. Крускала Уоллис критерийі-бір уақытта екі, үш, төрт
Слайд 1Дисперсиялық талдаудың
бір факторлы параметрлік емес
ұқсастығы критерий-
Крускал Уоллис критерийі
Слайд 2Жоспары:
І. Кіріспе
ІІ. Негізгі бөлім
а) Бірфакторлық дисперсиялық талдау.
б) Краскела-Уоллиса критериі.
в) Крускал-Уоллистің Н
ІІІ. Қорытынды.
ІV. Пайдаланылған әдебиеттер.
Бақылау сұрақтары
Факторлы дисперсиялық талдау мақсаты және есебі
Параметрлік емес талдау факторы: қолданылу шарттары
Крускал-Уоллис критерийі
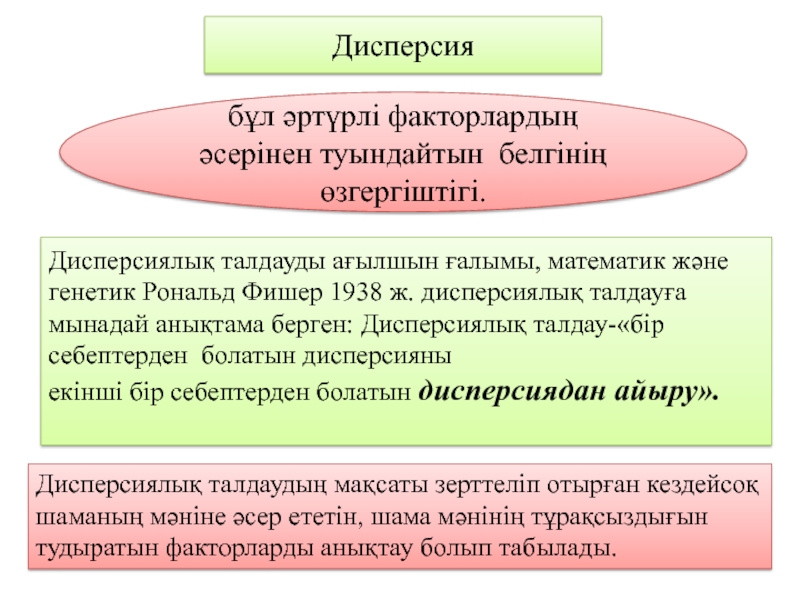
Слайд 3Дисперсия
бұл әртүрлі факторлардың әсерінен туындайтын белгінің өзгергіштігі.
Дисперсиялық талдауды ағылшын ғалымы,
екінші бір себептерден болатын дисперсиядан айыру».
Дисперсиялық талдаудың мақсаты зерттеліп отырған кездейсоқ шаманың мәніне әсер ететін, шама мәнінің тұрақсыздығын тудыратын факторларды анықтау болып табылады.
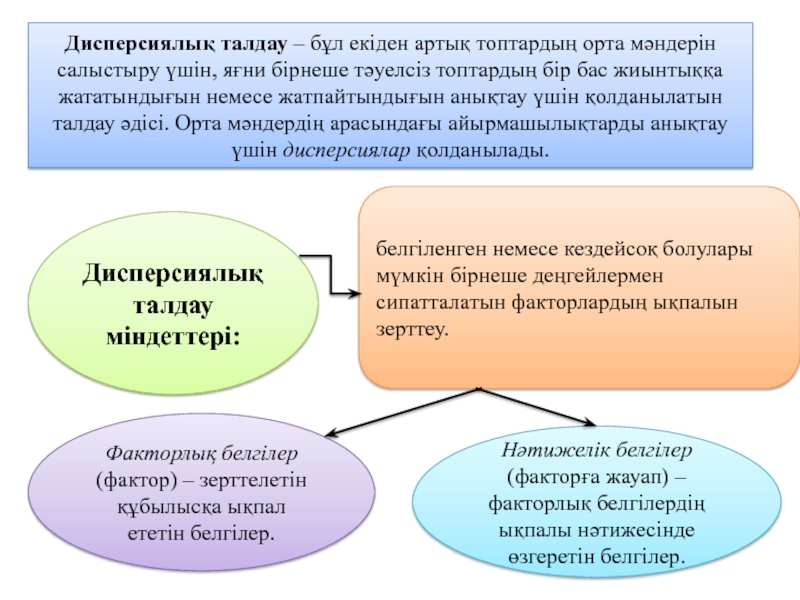
Слайд 4Дисперсиялық талдау міндеттері:
белгіленген немесе кездейсоқ болулары мүмкін бірнеше деңгейлермен сипатталатын факторлардың
Факторлық белгілер(фактор) – зерттелетін құбылысқа ықпал ететін белгілер.
Нәтижелік белгілер(факторға жауап) – факторлық белгілердің ықпалы нәтижесінде өзгеретін белгілер.
Дисперсиялық талдау – бұл екіден артық топтардың орта мәндерін салыстыру үшін, яғни бірнеше тәуелсіз топтардың бір бас жиынтыққа жататындығын немесе жатпайтындығын анықтау үшін қолданылатын талдау әдісі. Орта мәндердің арасындағы айырмашылықтарды анықтау үшін дисперсиялар қолданылады.
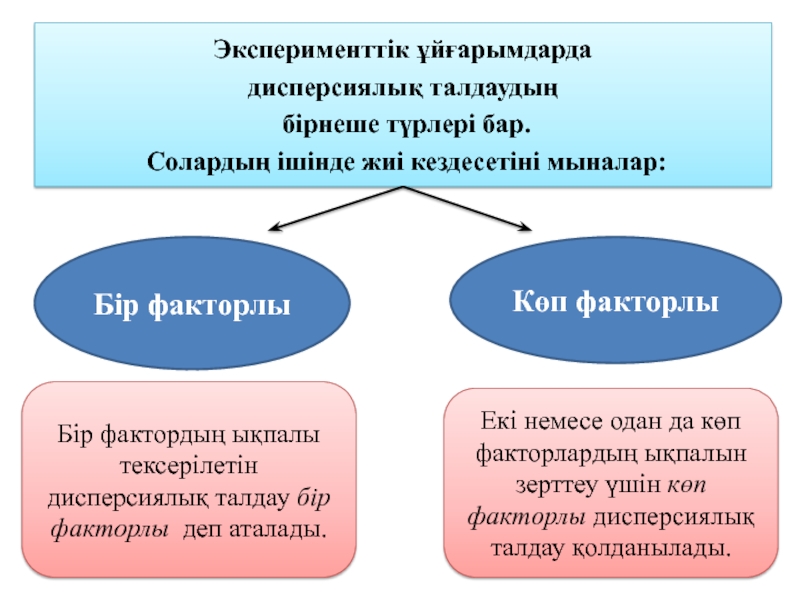
Слайд 5Эксперименттік ұйғарымдарда
дисперсиялық талдаудың
бірнеше түрлері бар.
Солардың ішінде жиі кездесетіні
Бір факторлы
Көп факторлы
Бір фактордың ықпалы тексерілетін дисперсиялық талдау бір факторлы деп аталады.
Екі немесе одан да көп факторлардың ықпалын зерттеу үшін көп факторлы дисперсиялық талдау қолданылады.
Слайд 6Бір факторлы дисперсиялық талдау
Мысалы: фактор - жыл мезгілі болса, онда оның
Фактор – емдеу тәсілдерінің түрі болса, онда оның деңгейлері: стандартты әдіспен емдеу, жаңа емдеу түріжәне плацебо (бақылау тобы) болуы мүмкін.Салыстырылатын топ саны – 3.
Дисперсиялық талдау жүргізу үшін сапалық белгілер (жыныс, профессия) де, сандық белгілер де (иньекция саны,аурулар саны) қолданылады.
Топтар бір фактордың деңгейлері арқылы анықталады. Бас жиынтықтағы айнымалы әр топта қалыпты таралған және барлық топтардың дисперсиялары бірдей.
Айырмашылықтын шамасын бағалау үшін таңдама орта мәндердің шашылуын топ ішіндегі мәндердің шашылуымен салыстыру қажет.
Салыстырылатын топтар саны фактордың (тәуелсіз айнымалы)деңгейлеріне сәйкес анықталады.
Слайд 7Дисперсиялық талдаудың негізгі идеясы:
Таңдама дисперсияны екі компенентке бөлу:
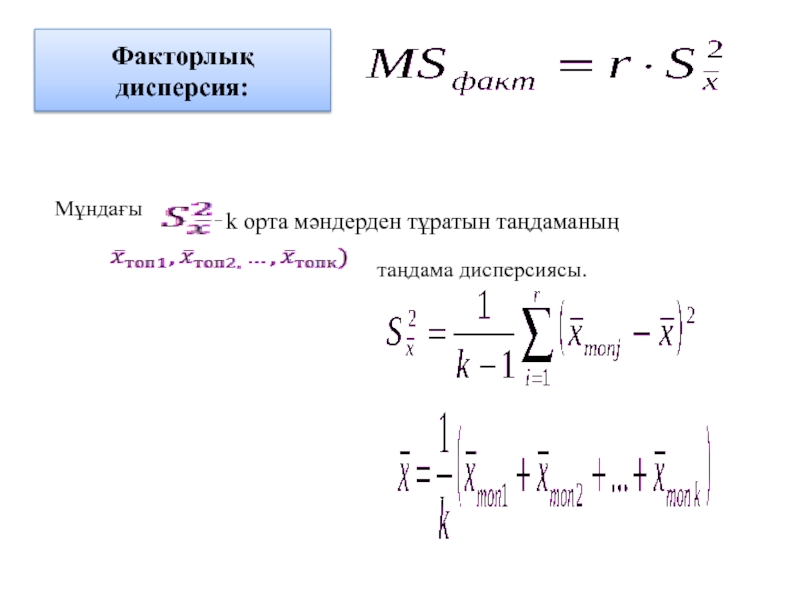
Факторлық дисперсия
Қалдық дисперсия.
Жалпы ортаға
Топтардың түзетілген таңдама дисперсиялары үшін орта арифметикалық мән болып табылатын қалдық дисперсияны топішілік дисперсия деп атайды.
Слайд 8Топтық орта мәндердің теңдігі жөніндегі нөлдік жорамалда топаралықдисперсия топішілік дисперсияға ұқсас.
ANOVA үшін Фишер критерийініңF статистикасы топаралық дисперсияның топішілік дисперсияға қатынасы арқылы анықталады.
F статистикасы (к- 1) және (n-к) еркіндік дәрежелеріне сәйкес келетін Фишер таралуына бағынады
Слайд 10Қалдық дисперсияны есептеу формуласы
мұндағы
үшін еркіндік дәржесінің саны (к – 1), мұндағы к-топтар саны.
үшін еркіндік дәрежесінің саны к·(r- 1), мұндағы r-әр топтағы мәндер саны, к - топтар саны,
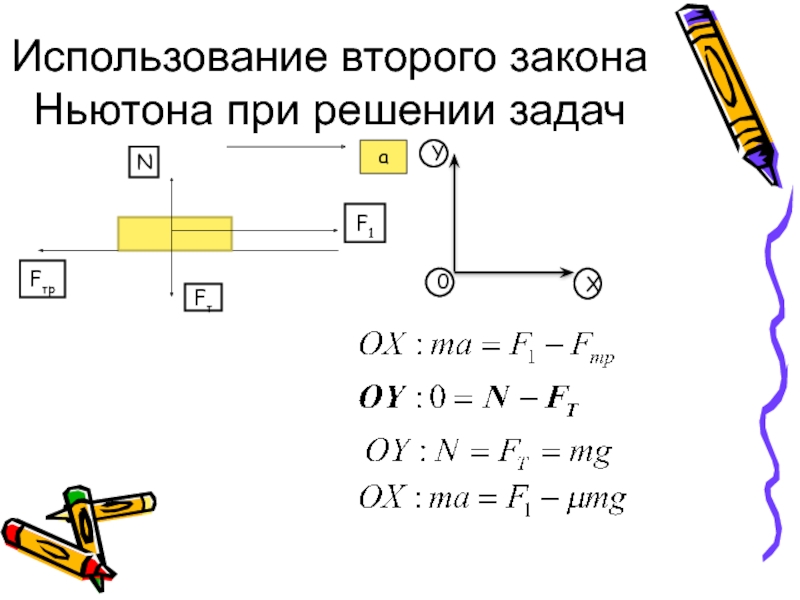
Слайд 11Бірфакторлық дисперсиялық талдау
Дисперсиялық талдауды жүргізу әдісі:
1. Нөлдік және балама жорамалдарды құрамыз:
Н0:
H1: таңдама орталар арасындағы айырмашылықтар кездейсоқ емес және оларға фактор ықпал етеді.
2. α мәнділік деңгейі беріледі ( мысалы, α=0,05 немесе α=0,01).
Слайд 14Краскел-Уоллиса критерийі бірнеше таңдамалылардың медиандарын тексеруге арналған. Уилкоксона — Манна —
Слайд 15Крускала Уоллис критерийі-бір уақытта екі, үш, төрт иаңдаулардың арасындағы айырмашылықтарды бағалайды.
Крускала-уоллистің
Н критерийі байланысты емес таңдамалар үшін бір факторлы дисперсионды анализдің параметрлік емес аналогтық әдісі ретінде қарастырылады. Баолық индивидуалды мәндер бір үлкен таңдама ретінде рангыленеді. Сосын барлық индивидуалды мәндер алғашқы таңдамаларға біріктіріледі. Сосын әрбір таңдама бойынша сол мәндердің алған рангтарын санаймыз. Егер таңдамалар арасындағы өзгешеліктер кездейсоқ болсарангтардың қосындысы ношалықты мәнді түрде өзгешеленбейді. Себебі таңдамалар арасындағы рангтардың жоғары төмен мәндері біртекті үлестіріледі.