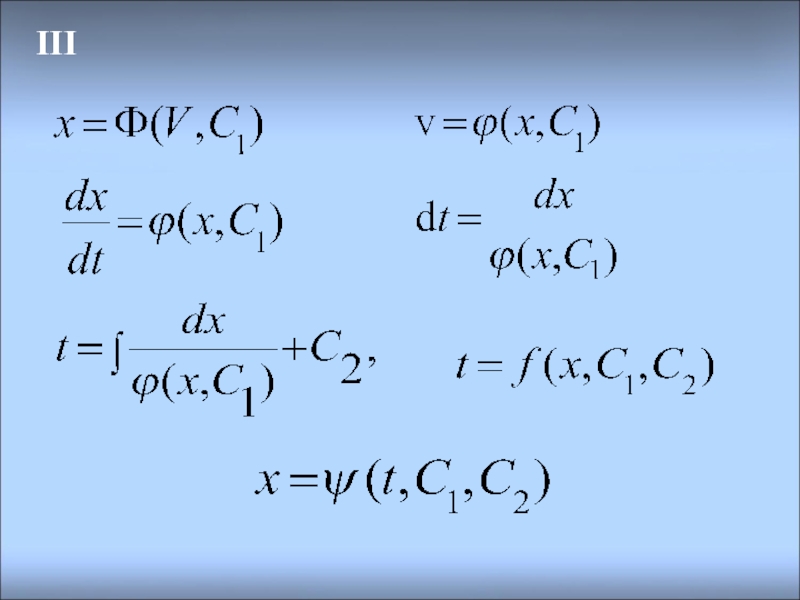- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика материальной точки. (Лекция 1) презентация
Содержание
- 1. Динамика материальной точки. (Лекция 1)
- 2. План лекции 1. Введение. Предмет и задачи
- 3. Цель лекции Познакомиться с основными законами динамики материальной точки и методами решения задач динамики точки.
- 4. Вспомним, что мы уже изучили: Теоретическая механика
- 5. Предмет и задачи динамики Динамика –
- 6. Предмет и задачи динамики При решении
- 7. Если на материальную точку не действуют никакие
- 8. Законы Ньютона II Закон Ньютона Сила, действующая
- 9. Законы Ньютона Силы, с которыми действуют друг
- 10. Принцип независимости действия сил Если на материальную
- 11. Дифференциальные уравнения движения материальной точки
- 12. Дифференциальные уравнения движения материальной точки Естественная форма
- 13. Решение первой (прямой) задачи динамики Условие задачи:
- 14. Пример Точка массой m движется в
- 15. Решение второй (обратной) задачи динамики Известна сила,
- 16. Общее решение системы (6) Постоянные
- 17. При t = 0 Подчиняя (7)
- 18. Пример Самолет летит на высоте 400м
- 19. Начальные условия При t = 0 Закон движения груза:
- 20. Прямолинейное движение материальной точки Точка будет совершать
- 21. I Сила зависит от времени
- 22. II Сила зависит от положения точки
- 23. II
- 24. III Сила зависит от скорости точки
- 25. III Другой способ решения:
- 26. III
- 27. Рекомендации к решению обратной (и смешанной) задачи
- 28. Пример (фантастический проект). Для перевозки грузов
- 29. Пример (фантастический проект). 3.
- 30. Пример (фантастический проект).
- 31. Заключение 1. Сформулированы основные задачи динамики точки
- 32. Вопросы для самоконтроля Что изучается в динамике?
- 33. Вопросы для самоконтроля 9. Почему масса точки
- 34. Тема следующей лекции Колебательное движение точки
Слайд 1ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
Новосибирский Государственный Архитектурно-Строительный Университет (Сибстрин)
Кафедра теоретической механики
ЛЕКЦИЯ
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Слайд 2План лекции
1. Введение. Предмет и задачи динамики.
2. Дифференциальные уравнения движения материальной
3. Решение прямой задачи динамики.
4. Рекомендации к решению обратной (и смешанной) задачи.
5. Примеры
Заключение
Слайд 3Цель лекции
Познакомиться с основными законами динамики материальной точки и методами решения
Слайд 4Вспомним, что мы уже изучили:
Теоретическая механика – изучает движение тел при
Единственная мера взаимодействия – сила.
Три раздела курса – статика, кинематика, динамика.
Статика – изучает частный случай движения – равновесие. Основной результат:
Если эти уравнения не выполняются – тело будет двигаться!
Кинематика – изучает движение тел без учета сил – т.е. закон движения тела, траекторию, скорость, ускорение отдельных точек , связи между ними.
Слайд 5Предмет и задачи динамики
Динамика – изучает движение тел под действием
Силы будем считать зависящими от времени, от положения точек, от скоростей точек.
Две основные задачи динамики:
По заданному закону движения определить силы (эта задача уже решена была в кинематике!)
По заданным силам определить закон движения (для ее решения еще нужно задать массу и дополнитель-ные условия, например, положение и скорости точек в начальный момент времени).
Замечание. Есть еще одна задача – “смешанная”. В ней заданы часть сил и часть закона движения. Требуется найти остальное (например: задана линия движения точки и активные силы, найти силы реакции и закон движения по линии)
Слайд 6Предмет и задачи динамики
При решении этих задач мы будем опираться
применять принцип отвердевания
пользоваться способами приведения сил
применять методы задания движения тел
использовать связи между скоростями и ускорениями отдельных точек.
Также как и в статике и в кинематике, начнем изучать динамику с движения точки.
Напомним: Материальная точка – тело конечной массы, размерами которого пренебрегаем.
Слайд 7 Если на материальную точку не действуют
никакие силы, то эта точка или
покое, или движется прямолинейно и
равномерно.
Законы Галилея-Ньютона
I Закон Ньютона (закон инерции Галилея)
Слайд 8Законы Ньютона
II Закон Ньютона
Сила, действующая на материальную точку,
сообщает ей ускорение, которое
системе отсчета пропорционально величине
силы и имеет направление силы.
Основное уравнение динамики:
Слайд 9Законы Ньютона
Силы, с которыми действуют друг на друга две материальные точки,
III Закон Ньютона
Слайд 10Принцип независимости действия сил
Если на материальную точку действуют несколько сил, то
Слайд 12Дифференциальные уравнения движения материальной точки
Естественная форма записи:
Спроектируем (1) на оси естественного
Слайд 13Решение первой (прямой) задачи динамики
Условие задачи:
Движение точки задано. Требуется найти силу,
Решение задачи:
Сводится к подстановке закона движения в уравнения (1), (3) или (4).
Слайд 14Пример
Точка массой m движется в плоскости х,у по закону х=2sin((π/6)t),
Слайд 15Решение второй (обратной) задачи динамики
Известна сила, действующая на материальную точку. Требуется
Слайд 16
Общее решение системы (6)
Постоянные С1, …. , С6 находятся из
В качестве начальных условий следует зафиксировать положение и скорость материальной точки в начальный момент времени.
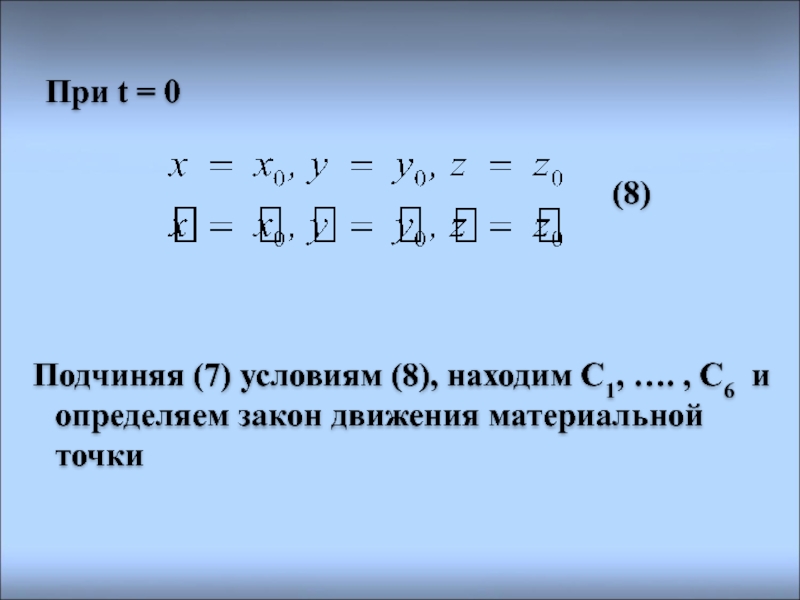
Слайд 17При t = 0
Подчиняя (7) условиям (8), находим С1, …. ,
Слайд 18Пример
Самолет летит на высоте 400м со скоростью 200 м/с. Найти
Считаем груз материальной точкой
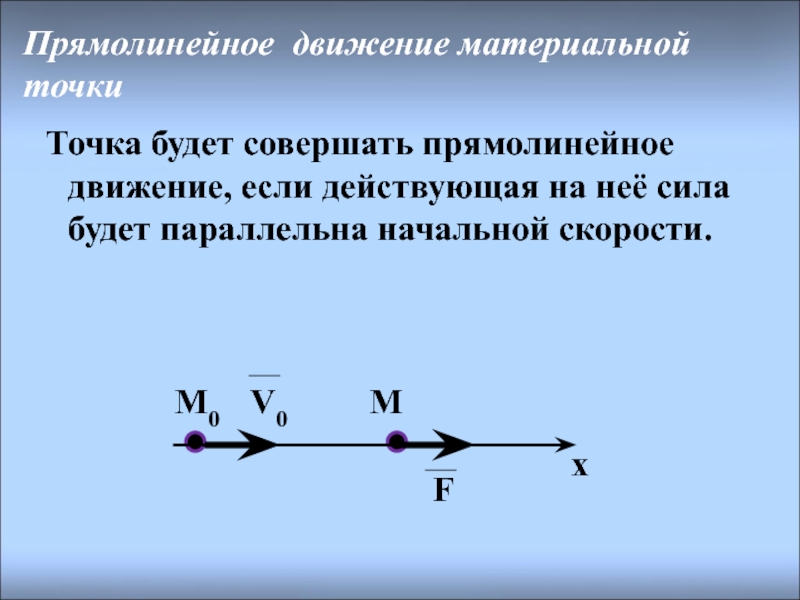
Слайд 20Прямолинейное движение материальной точки
Точка будет совершать прямолинейное движение, если действующая на
Слайд 27Рекомендации к решению обратной (и смешанной) задачи динамики точки
Выбрать систему координат
Изобразить все силы (активные и реакции связей), действующие на точку.
Написать второй закон Ньютона в векторном виде, спроецировать его на оси координат и получить ДУ.
Написать НУ(точнее дополнительные условия)
Решить ДУ с использованием НУ.
Замечания:
Полезен нулевой пункт: Прежде чем решать – подумай!
Уместна пословица: Заставь дурака богу молиться – он и лоб пробьет!
Слайд 28Пример (фантастический проект).
Для перевозки грузов из Н в L прорыт
Решение.
1. Начало отсчета поместим в Н,
а ось x направим в сторону L.
2. На груз будет действовать сила
притяжения Земли
и нормальная реакция гладкого канала .
Слайд 29Пример (фантастический проект).
3.
Т.к. масса сокращается, то для любых грузов
4. НУ:
5.
Слайд 30Пример (фантастический проект).
Проанализируем решение.
груз до L доедет (!), причем
. Отметим что время не зависит от расстояния (что до L, что до Омска время прибытия груза одно и то же!) . Скорость, с которой груз доедет, будет равна
Причем, если груз не забрать в L, то он поедет обратно в Н.
Слайд 31Заключение
1. Сформулированы основные задачи динамики точки – прямая, обратная и смешанная.
2.
3. Выведены ДУ движения точки в прямоугольной декартовой и естественной системах отсчета.
4. Даны рекомендации к решению обратной и смешанной задачи.
5. Приведены примеры решения задач.
Слайд 32Вопросы для самоконтроля
Что изучается в динамике?
Какие основные задачи динамики?
В чем суть
Какие системы отсчета называют инерциальными, а какие неинерциальными?
Как связаны между собой две инерциальные системы отсчета?
Почему систему отсчета, связанную с Землей в большинстве случаев приближенно принимают за инерциальную?
Сформулируйте условия, при которых справедлив второй закон Ньютона?
В чем состоит принцип суперпозиции действия сил на точку?
Слайд 33Вопросы для самоконтроля
9. Почему масса точки является мерой ее инерции?
10. Как
11. Для чего нужны дифференциальные уравнения движения точки?
12. Сформулируйте прямую и обратную задачи динамики точки? Все ли задачи динамики точки сводятся к этим двум?
13. Перечислите основные этапы решения обратной задачи динамики точки?
14. Для чего необходимо задавать начальные (дополнительные) условия при решении обратной задачи динамики точки? Сколько таких условий требуется задавать?