Теплопередача при стационарном режиме презентация

через разделяющую их перегородку. Теплопередача является сложным видом теплообмена, в котором участвуют две среды и тело. Кроме того, в нём действуют одновременно и совместно все элементарные явления переноса теплоты (теплопроводность, конвекция, лучеиспускание).
Количество переданной теплоты теплопередачей при стационарном режиме определяется по основному уравнению теплопередачи:

Q = K⋅F⋅Δt, Вт,
где Q – количество переданной теплоты, Вт.
Δt – tг – tх, оС.
tг – температура горячего теплоносителя, оС;
tх – температура холодного теплоносителя, оС;
F – теплообменная поверхность, м2;
K – коэффициент теплопередачи, размерность которого получается из
основного уравнения:
 
[K] = [Q/FΔt] = [Вт/м2 ⋅ град]
 
Коэффициент теплопередачи представляет собой количество теплоты, переданной через единицу поверхности в единицу времени от одного теплоносителя к другому при разности температур между ними в один градус. Коэффициент теплопередачи связывает между собой коэффициент теплопроводности и теплоотдачи.

однородной плоской стенкой. Коэффициент теплопроводности стенки - λ и толщина её - δ. Температура - tC1 и tC2, причём tC1 > tC2. Температура поверхностей стенки неизвестны, обозначим их как tn1 и tn2. Суммарный коэффициент теплоотдачи со стороны горячего теплоносителя равен α1, а со стороны холодного - α2.

По условию задачи температурное поле одномерно, режим стационарный. В этом случае вся теплота, переданная от горячего теплоносителя к поверхности стенки, проходит сквозь стенку и отдаётся холодному теплоносителю, т.е. указанные количества теплоты равны между собой.

Следовательно, для теплового потока q, где q = Q/Fτ, можно написать систему из трёх уравнений:

(1)
 
 
Из уравнений (1) находятся частные температурные напоры:
 
 
  (2)



После сложения левых и правых частей уравнений (2) получается выражение для полного температурного напора
tC1 - tC2 = q(1/α1 + δ/λ + 1/α2), (3)
 откуда определяется значение удельного теплового потока:
 
(4)
 
 

температур между двумя теплоносителями и обратно пропорционален сумме термических сопротивлений.

Вводя обозначение: К = 1/(1/α1 + δ/λ + 1/α2) в выражение (4), получим:

q = K(tC1 - tC2)
 
Величина К называется коэффициентом теплопередачи. Он устанавливает связь между элементарными видами теплообмена через коэффициенты теплоотдачи и коэффициенты теплопроводности.
Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи:
 
1/K = 1/α1 + δ/λ + 1/α2 , [м2⋅град/Вт]
 
где δ/λ - термическое сопротивление стенки
1/α1 и 1/α2 - являются термическими сопротивлениями теплоотдачи от
горячего теплоносителя к холодному.

tC1 - tC2). Температуры поверхностей стенки неизвестны, обозначим их через tn1 и tn2. Коэффициент теплоотдачи от горячей жидкости, протекающей внутри трубы, равен α1, а к холодной - α2.
В условиях стационарного режима количество теплоты, отданное горячей и воспринятое холодной жидкостями, одно и то же, следовательно, можно написать:
 
(1)
 
 
 
Решив эти уравнения относительно разности температур, получим:
 
 
 
(2)
 
 

(3)
 
Откуда значение теплового потока
 
(4)
 
Введём следующее обозначение
 
(5)
 

После подстановки этого равенства в (4) окончательно получим:
 
ql = Кl ⋅ π ⋅ (tC1 - tC2),
 
здесь Кl – коэффициент теплоотдачи, отнесённый к единице длины трубы.

процессы протекают, например, в том случае, если с одной стороны стенки конденсируется пар, а с другой – кипит жидкость. Наиболее часто теплопередача в промышленной аппаратуре протекает при переменных температурах теплоносителей.
Температуры теплоносителей обычно изменяются вдоль поверхности, разделяющей их стенки.
Теплопередача при переменных температурах зависит от взаимного направления движения теплоносителей. В непрерывных процессах теплообмена возможны следующие варианты направления движения жидкостей друг относительно друга вдоль разделяющей их стенки:
1) параллельный ток, или прямоток, при котором теплоносители движутся в одном и том же направлении;
2) противоток, при котором теплоносители движутся в противоположных направлениях;
3) перекрёстный ток, при котором теплоносители движутся взаимно перпендикулярно друг другу;
4) смешанный ток, при котором один из теплоносителей движется в одном направлении, а другой – как прямотоком, так и противотоком к первому.

зависимости от вида взаимного направления движения теплоносителей. Поэтому в уравнение теплопередачи следует подставлять среднее значение температурного напора
Q = K⋅F⋅Δtm (1)
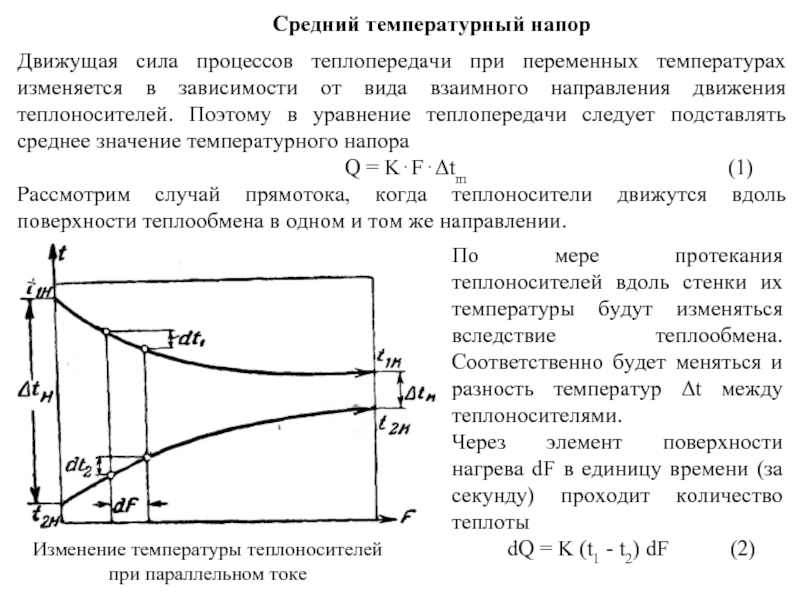
Рассмотрим случай прямотока, когда теплоносители движутся вдоль поверхности теплообмена в одном и том же направлении.

По мере протекания теплоносителей вдоль стенки их температуры будут изменяться вследствие теплообмена. Соответственно будет меняться и разность температур Δt между теплоносителями.
Через элемент поверхности нагрева dF в единицу времени (за секунду) проходит количество теплоты
dQ = K (t1 - t2) dF (2)

Изменение температуры теплоносителей при параллельном токе

dt1 = - dQ/G1C1 (3)

менее нагретой повысится на dt2 = - dQ/G2C2, где

G1 – количество протекающей в единицу времени горячей жидкости
C1 – её теплоёмкость
G2 – количество протекающей в единицу времени холодной жидкости
C2 – её теплоёмкость

Знак “минус” указывает на охлаждение более нагретого теплоносителя в процессе теплообмена.

Произведение G⋅C назовём водяным эквивалентом и обозначим G1⋅C1 = W1; G2⋅C2 = W2
 
и
1/W1 + 1/W2 = m (4)

нагретой жидкости из величины изменения температуры более нагретой жидкости
 

 


откуда dQ = - d(t1 - t2)/m (5)
 
Подставив найденное значение (5) в уравнение (2) получим
 
d(t1 - t2)/m = - K (t1 - t2) dF (6)
 
Заменим t1 – t2 на Δt и разделим переменные на Δt
 
d Δt/ Δt = - K m dF (7)

Δtконеч и от 0 до F
 
(8)

 
ln Δtкон / Δtнач = - mRT (9),
где Δtнач – (t1нач – t2нач) начальная разность температур,
Δtкон – (t1кон – t2кон) конечная разность температур.
Уравнение теплового баланса для элемента поверхности df имеет вид
Q = G1⋅C1 (t1нач – t1кон) = G2⋅C2 (t2кон - t2нач) (10),
а так как
G1⋅C1 = W1, G2⋅C2 = W2, из уравнения (10) находим
 
Q/W1 = t1нач – t1кон и W2 = t2кон - t2нач (11)
Складывая эти выражения и учитывая уравнение (4) получим
 
Q(1/W1 + 1/W2) = (t1нач – t1кон) + (t2кон - t2нач),
 
откуда m = Δtнач -Δtконеч/Q (12)
 

(13)
 

откуда (14)
 
Сравнивая (14) с основным уравнением теплоотдачи (1), получим
 
(15)


(16)
 

Уравнение (16) остаётся верным и для определения среднелогарифмического температурного напора при движении жидкости противотоком.

удовлетворяется условие
 
Δtнач / Δtкон < 2, то средний температурный напор можно вычислять как среднее
арифметическое из крайних напоров
 
Δtср = (Δtнач - Δtкон)/2

Для смешанного тока и перекрёстного тока
 
Δtm = εΔt ⋅ Δtпр, где εΔt – поправочный коэффициент к средней разности
температур Δtпр, вычисленный для противотока.

длине трубы. Например, обозначим через T – температуру горячего теплоносителя и через t – холодного теплоносителя. Если
 
Δt = tк – tн < ΔT = Tн – Tк, то
 
tср = 0,5(tн – tк)
 
Tср = tср + Δtm
 
Если Δt > ΔT, то Tср = 0,5(Tк + Tк)
tср = Tср - Δtm
 
Если задана температура поверхности стенки, соприкасающейся с жидкостью, то
tср.ж = tст ± Δtm, где Δtm – средняя разность температур между стенкой и
жидкостью.

нанесения на стенку слоя тепловой изоляции.
Тепловой изоляцией называется всякое вспомогательное покрытие, которое способствует снижению потери теплоты в окружающую среду. Выбор и расчёт изоляции производится с учётом соображений экономического характера и требований технологии и санитарии.
Толщина изоляции для плоских стенок определяется из формулы:
 

 

Для трубопроводов из формулы:
 

 

где d2 – диаметр изолированного трубопровода.

расчётное уравнение входит не только в форме ln d2/d1, но и в виде члена 1/α2d2. Тепловые потери изолированных трубопроводов уменьшаются не пропорционально увеличению толщины изоляции. Это обстоятельство объясняется тем, что при увеличении толщины термическое сопротивление слоя изоляции увеличивается
 
 
а термическое сопротивление теплоотдачи в окружающую среду уменьшается:
 
 
Во избежание большой толщины при изоляции трубопроводов применяют материалы с малым коэффициентом теплопроводности. Максимальные тепловые потери наблюдаются при некотором значении диаметра, который называется критическим диаметром изоляции.
 
d2кр = 2λ/α2 , где λ - теплопроводность изоляции
α2 – коэффициент теплоотдачи от поверхности в
окружающую среду.