- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика материальной точки презентация
Содержание
- 1. Динамика материальной точки
- 2. Содержание 11. Работа
- 3. Законы Ньютона – постулаты являются
- 4. Второй закон Ньютона Масса - количественная
- 5. изменение импульса тела равно импульсу действовавшей на
- 6. Третий закон Ньютона
- 7. Закон сохранения импульса
- 8. Центр масс
- 9. Принцип относительности Галилея
- 10. Принцип относительности Галилея
- 11. В природе существует 4 вида фундаментальных
- 15. Деформация
- 16. Деформация сжатия-растяжения
- 18. Экспериментальная зависимость механического напряжения от относительной
- 20. Относительное поперечное сжатие
- 29. Кинетическая энергия Пусть под действием
- 30. Потенциальная энергия в однородном поле
- 31. Потенциальная энергия упругой деформации Внешняя
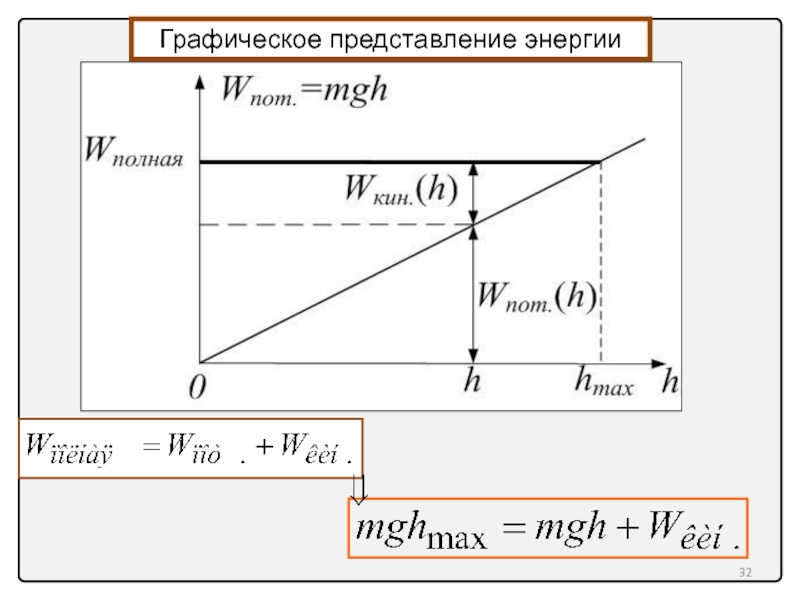
- 32. Графическое представление энергии
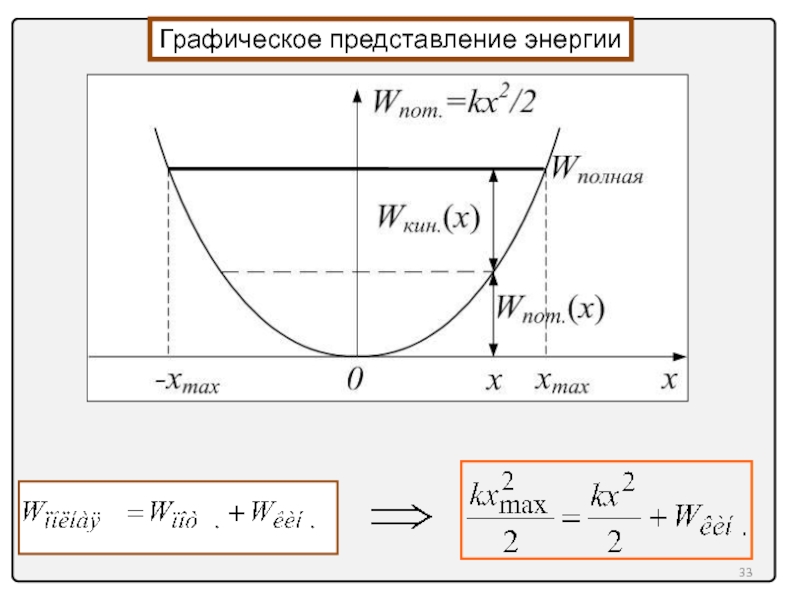
- 33. Графическое представление энергии
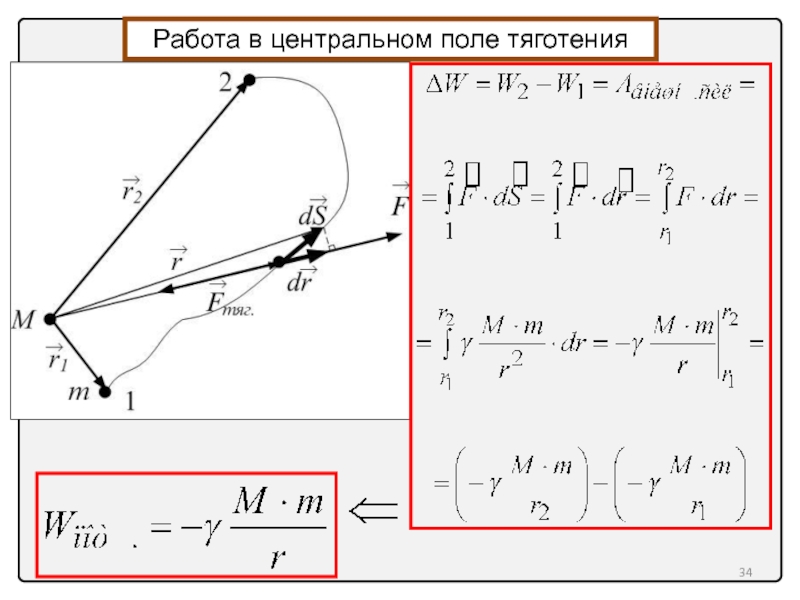
- 34. Работа в центральном поле тяготения
- 35. Работа в центральном поле тяготения
- 38. Градиент – это вектор, компоненты которого
- 39. Градиент показывает быстроту изменения величины в
- 40. Условие равновесия
Слайд 1
Содержание
1. Законы Ньютона: область применимости
2. Первый закон Ньютона. Инерциальные и
3. Второй закон Ньютона. Импульс тела
4. Третий закон Ньютона. Закон сохранения импульса
5. Центр масс
6. Принцип относительности Галилея. Преобразования Галилея. Закон сложения скоростей в классической механике. Второй закон Ньютона для неинерциальных систем отсчёта
7. Виды сил
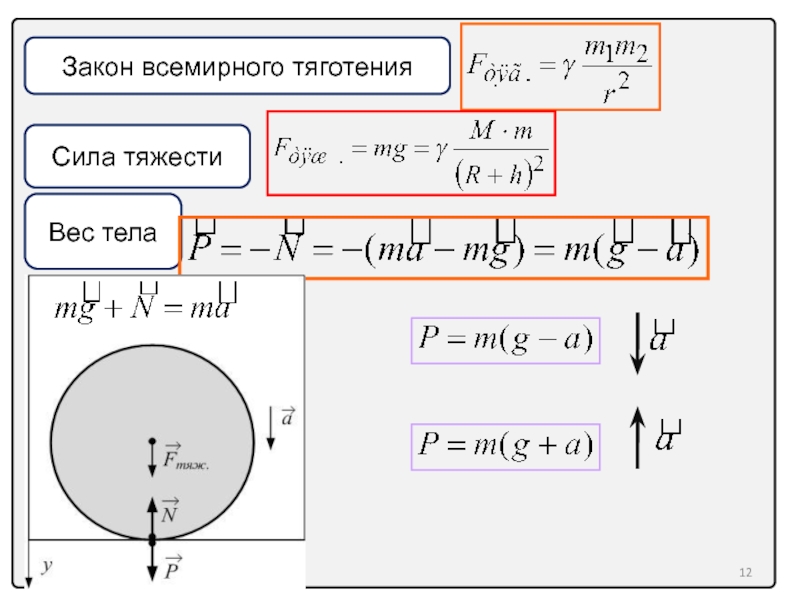
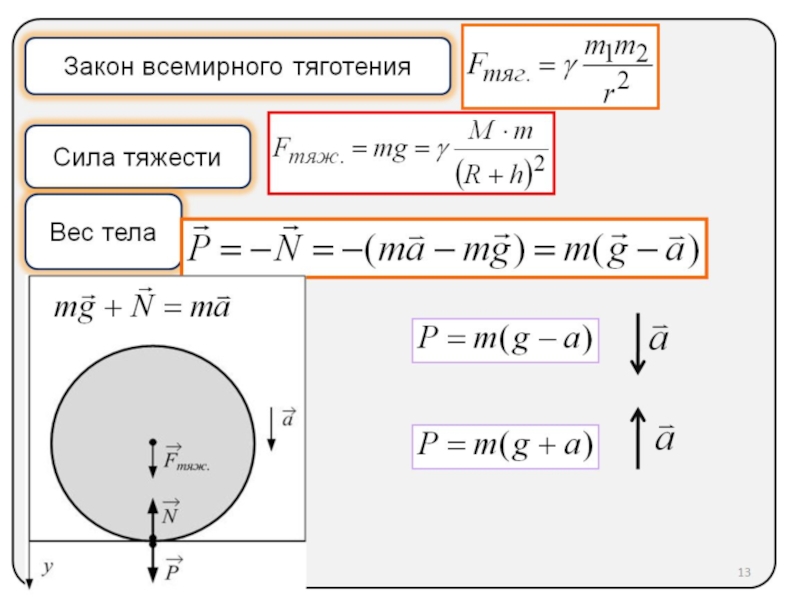
8. Закон всемирного тяготения. Сила тяжести. Вес тела
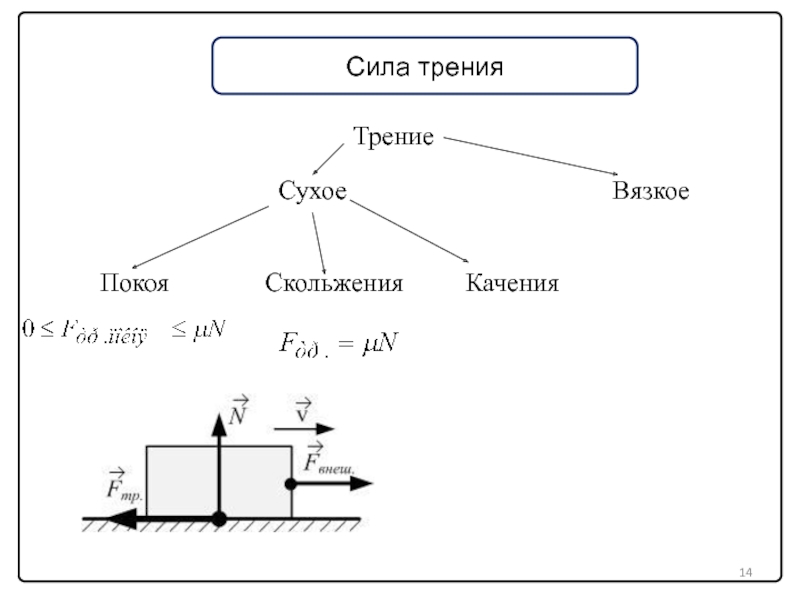
9. Сила трения
10. Силы упругости
Слайд 2
Содержание
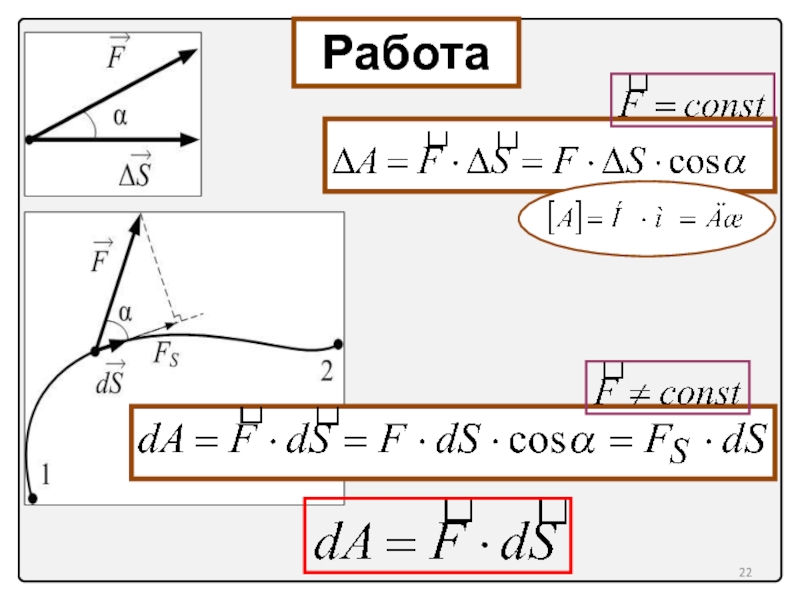
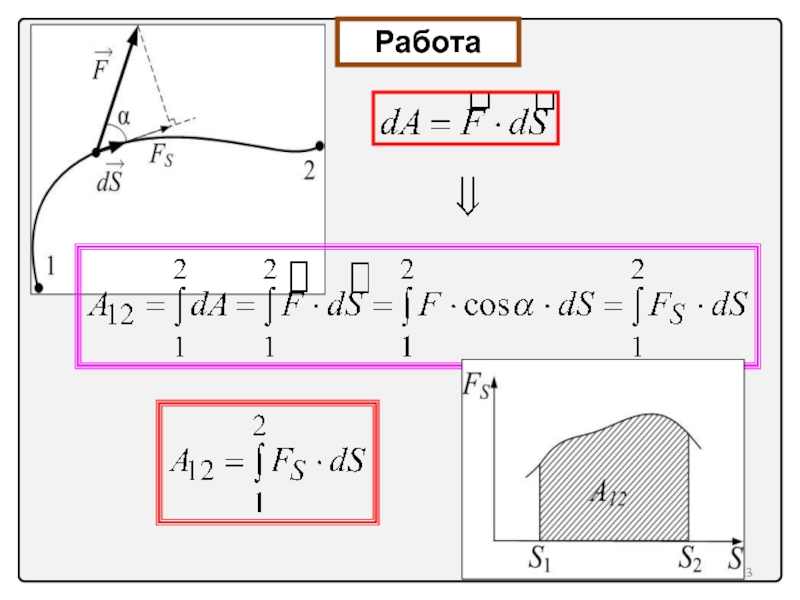
11. Работа
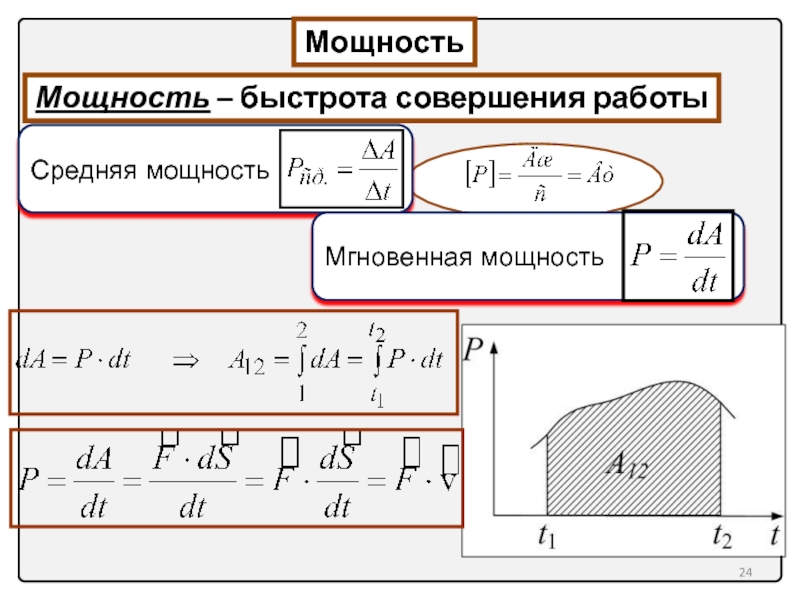
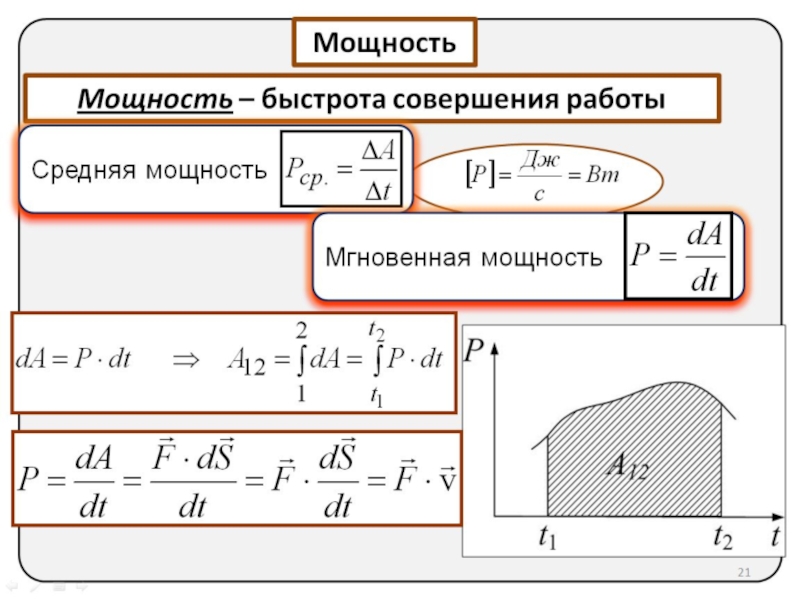
12. Мощность
13. Энергия. Закон сохранения энергии
14. Кинетическая энергия
15. Потенциальная энергия
16. Потенциальная энергия упругой деформации
17. Графическое представление энергии
18. Признак потенциальности поля. Консервативные силы. Диссипативные силы
19. Связь между консервативной силой и потенциальной энергией
Слайд 3
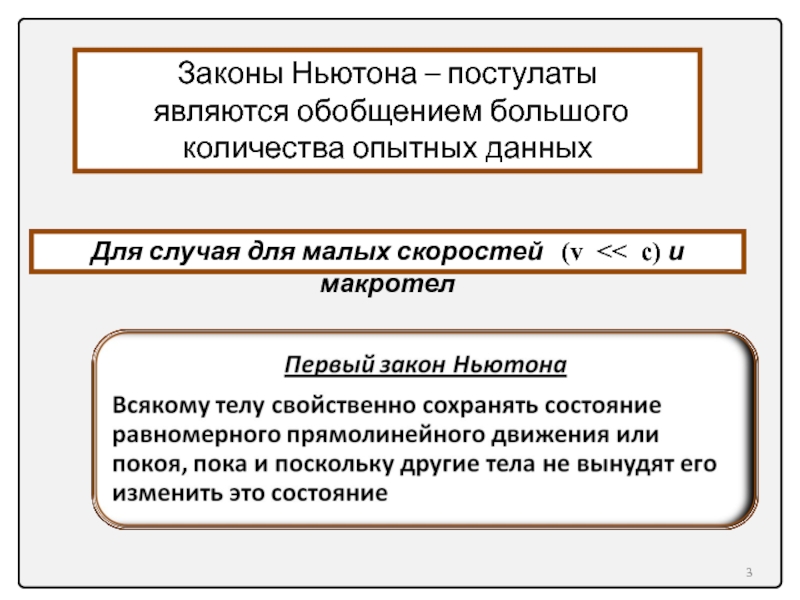
Законы Ньютона – постулаты
являются обобщением большого количества опытных данных
Для случая
Слайд 4
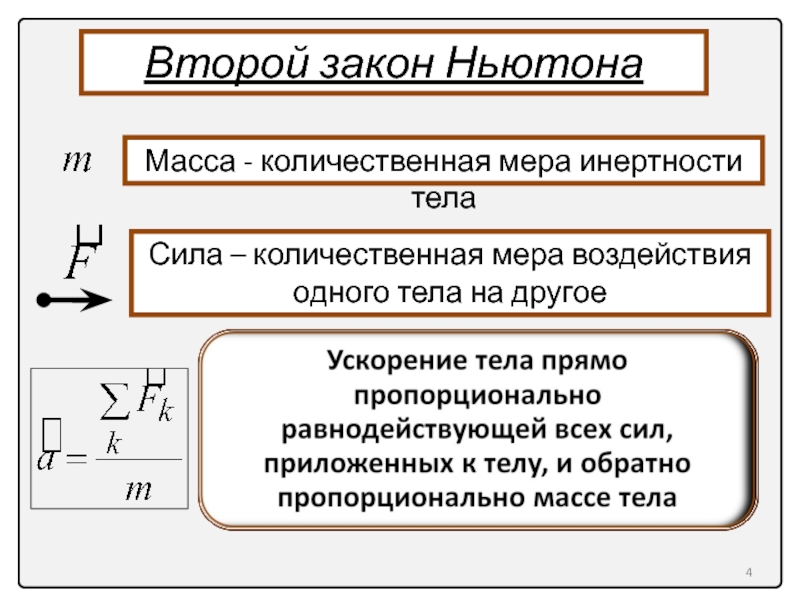
Второй закон Ньютона
Масса - количественная мера инертности тела
Сила – количественная мера
Слайд 5изменение импульса тела равно импульсу действовавшей на тело силы
Второй закон Ньютона
в
Изменение импульса тела равно импульсу действовавшей на тело силы
- импульс силы
- импульс тела
Слайд 6
Третий закон Ньютона
Силы, с которыми тела действуют друг на друга, равны
Всякое действие тел друг на друга носит характер ВЗАИМОдействия
Если система двух тел замкнута, по второму закону Ньютона:
Слайд 7
Закон сохранения импульса
Полный импульс системы сохраняется, даже если есть внешние силы,
В замкнутой системе полный импульс сохраняется
В проекциях:
Слайд 8
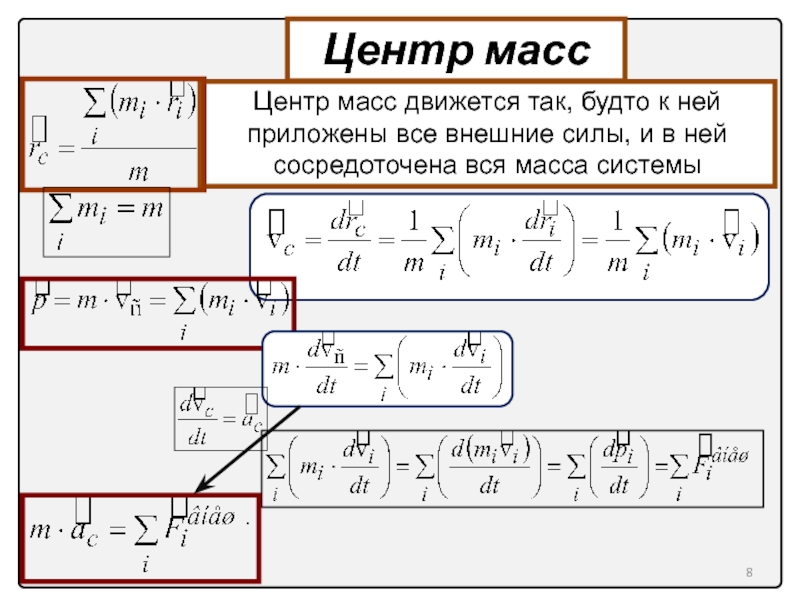
Центр масс
Центр масс движется так, будто к ней приложены все внешние
Слайд 9
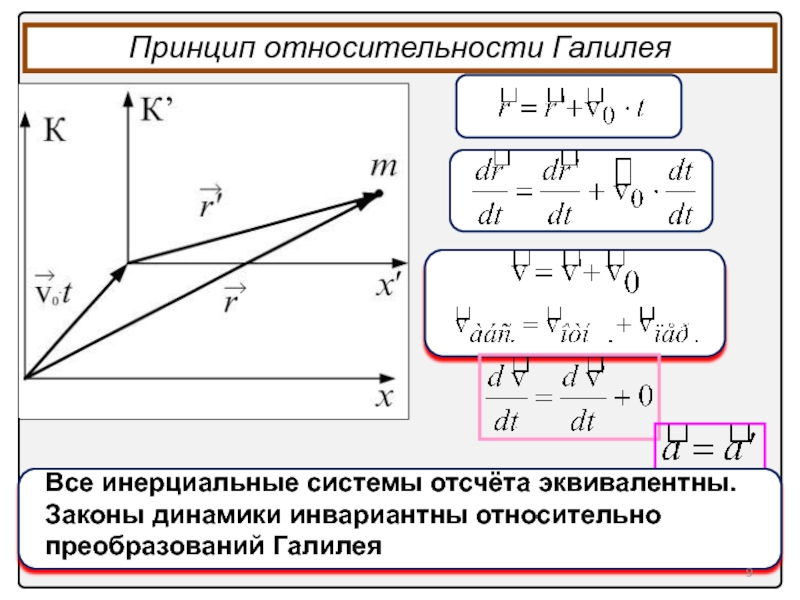
Принцип относительности Галилея
все инерциальные системы отсчёта эквивалентны. Или: законы динамики инвариантны
Все инерциальные системы отсчёта эквивалентны.
Законы динамики инвариантны относительно преобразований Галилея
Слайд 10
Принцип относительности Галилея
Второй закон Ньютона для неинерциальных систем отсчёта:
Преобразования
Галилея
В системе
В системе К’, движущейся с ускорением
, вводится сила инерции
Уравнение движения:
Слайд 11
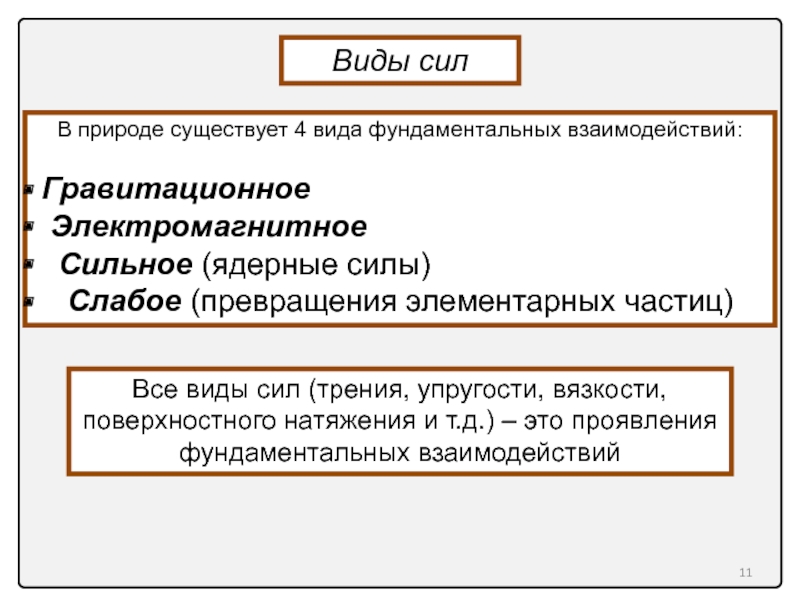
В природе существует 4 вида фундаментальных взаимодействий:
Гравитационное
Электромагнитное
Сильное
Слабое (превращения элементарных частиц)
Все виды сил (трения, упругости, вязкости, поверхностного натяжения и т.д.) – это проявления фундаментальных взаимодействий
Виды сил
Слайд 15
Деформация
Сжатия-
растяжения
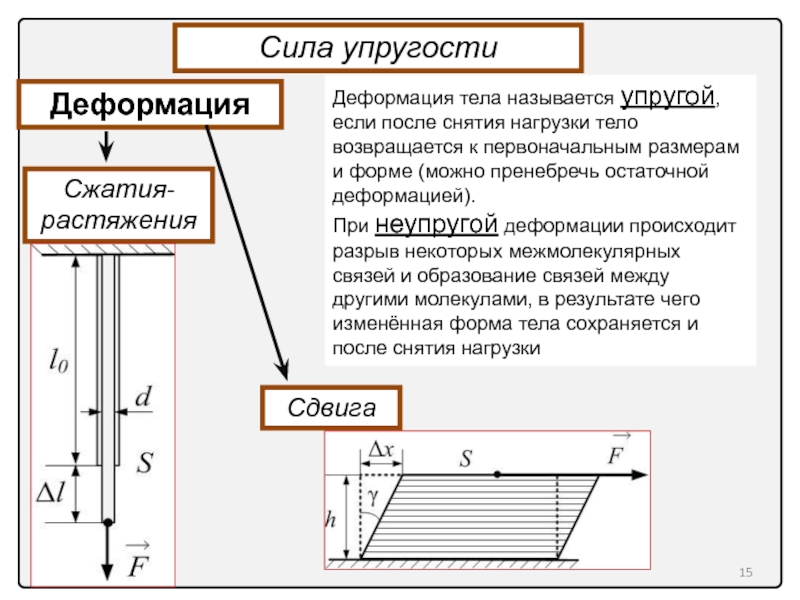
Сила упругости
Сдвига
Деформация тела называется упругой, если после снятия нагрузки тело возвращается
При неупругой деформации происходит разрыв некоторых межмолекулярных связей и образование связей между другими молекулами, в результате чего изменённая форма тела сохраняется и после снятия нагрузки
Слайд 16
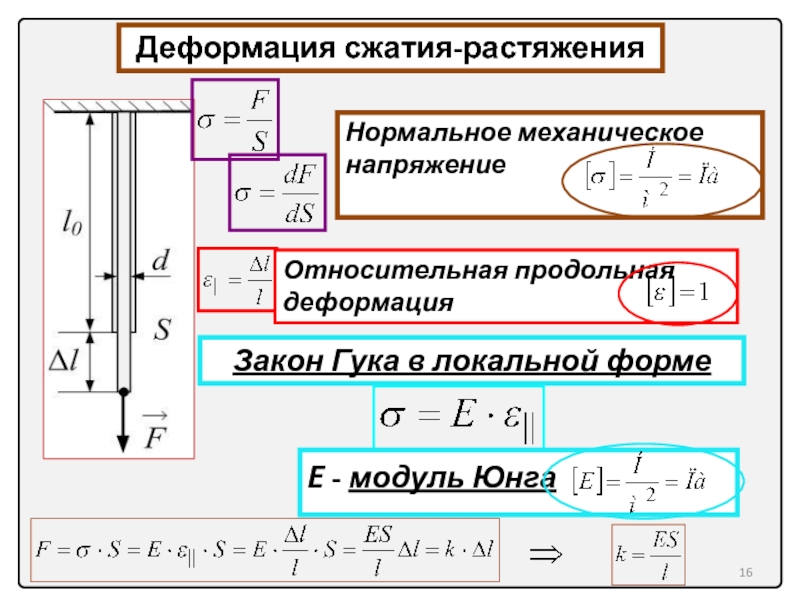
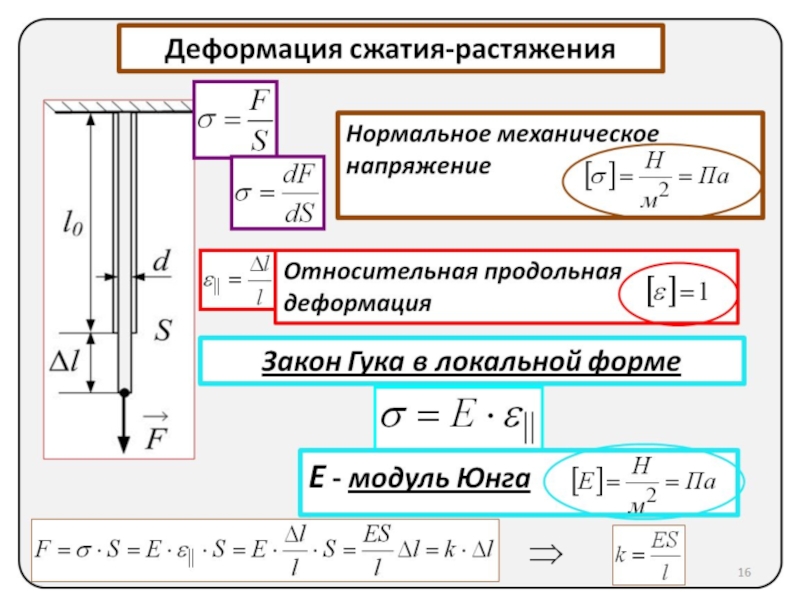
Деформация сжатия-растяжения
Нормальное механическое напряжение
Относительная продольная деформация
Закон Гука в локальной форме
E -
Слайд 18
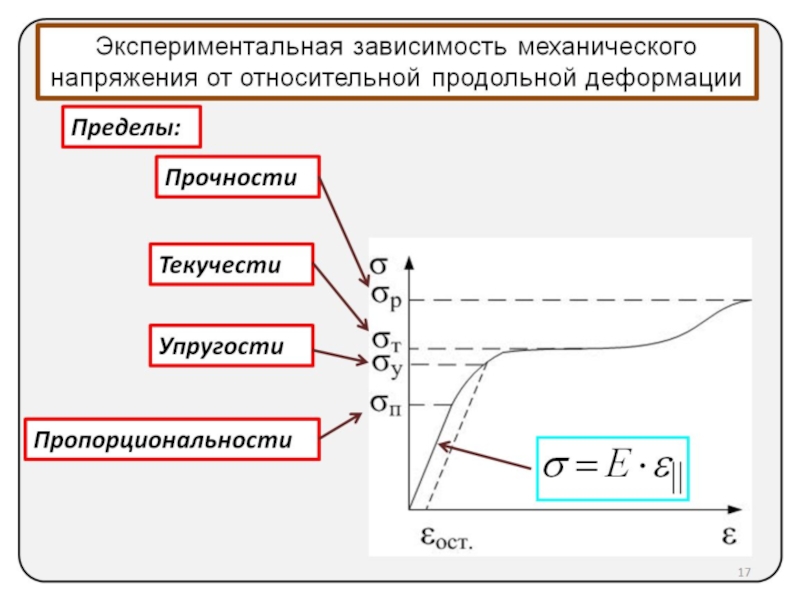
Экспериментальная зависимость механического напряжения от относительной продольной деформации
Пределы:
Пропорциональности
Упругости
Текучести
Прочности
Слайд 20
Относительное поперечное сжатие
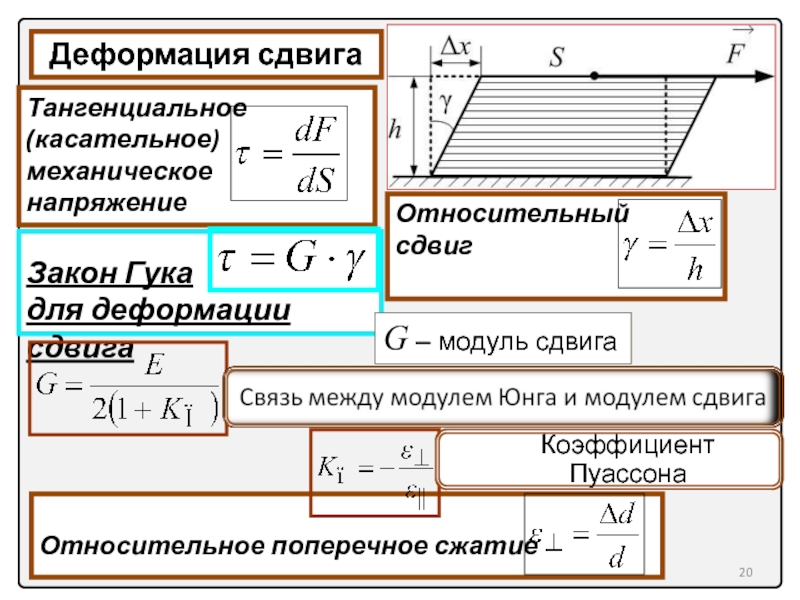
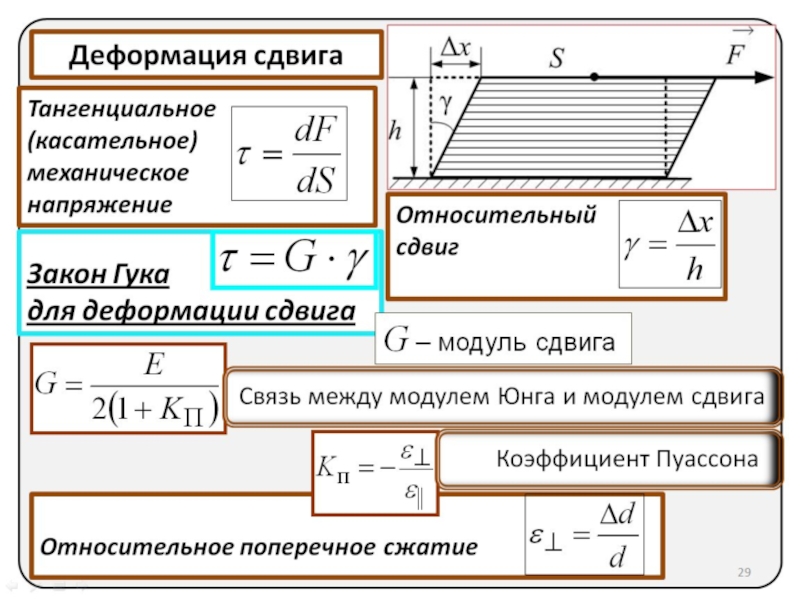
Деформация сдвига
Тангенциальное (касательное) механическое
напряжение
Относительный
сдвиг
Закон Гука
для
G – модуль сдвига
Слайд 26
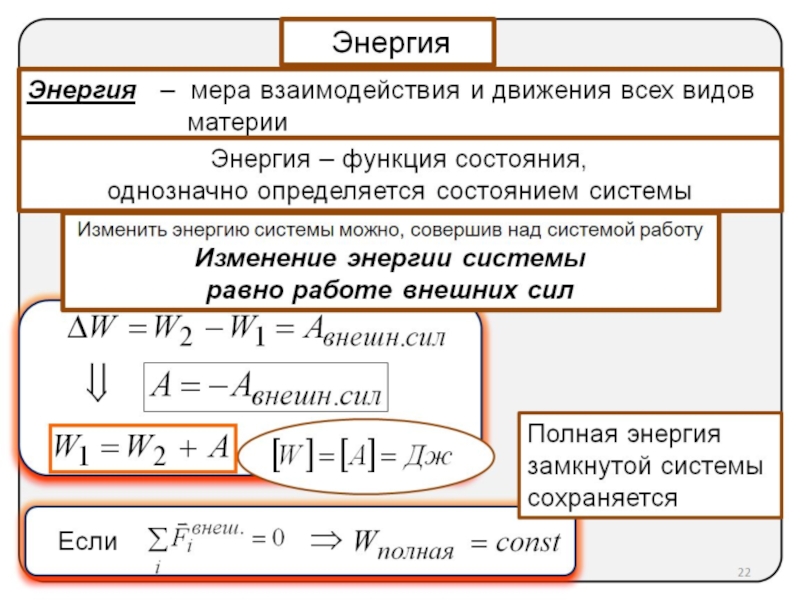
Энергия
Энергия – мера взаимодействия и движения всех видов
материи
Энергия –
однозначно определяется состоянием системы
Изменить энергию системы можно, совершив над системой работу
Изменение энергии системы
равно работе внешних сил
Если
Полная энергия замкнутой системы сохраняется
Слайд 29
Кинетическая энергия
Пусть под действием внешней силы скорость тела изменяется:
изменение энергии равно
Слайд 30
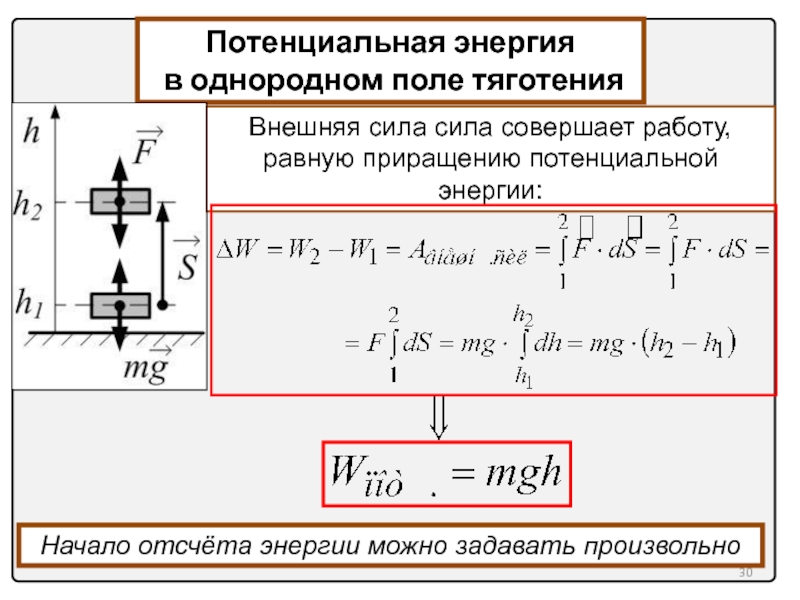
Потенциальная энергия
в однородном поле тяготения
Внешняя сила сила совершает работу, равную
Начало отсчёта энергии можно задавать произвольно
Слайд 31
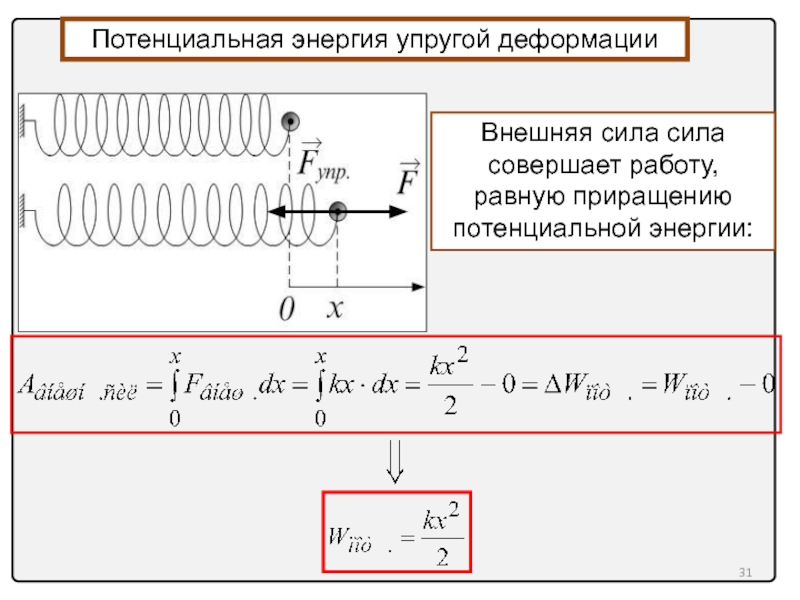
Потенциальная энергия упругой деформации
Внешняя сила сила совершает работу, равную приращению потенциальной
Слайд 35
Работа в центральном поле тяготения
Выводы:
2. Работа сил гравитационного поля не зависит
1. Потенциальная энергия взаимодействия точечных масс
(при )
3. Потенциал гравитационного поля:
Слайд 36
При наличии диссипативных сил механическая энергия необратимо превращается в другие виды,
Признак потенциальности поля
Консервативные силы
Диссипативные силы
Сила называется консервативной, если её работа не зависит от траектории, а только от начального и конечного положения тела
Поле таких сил называется потенциальным
Примеры: гравитационное поле; поле упругих сил
Если работа силы зависит от траектории, то силы называются диссипативными
Поле таких сил – непотенциальное
Примеры: силы трения; силы вязкости; силы неупругой деформации
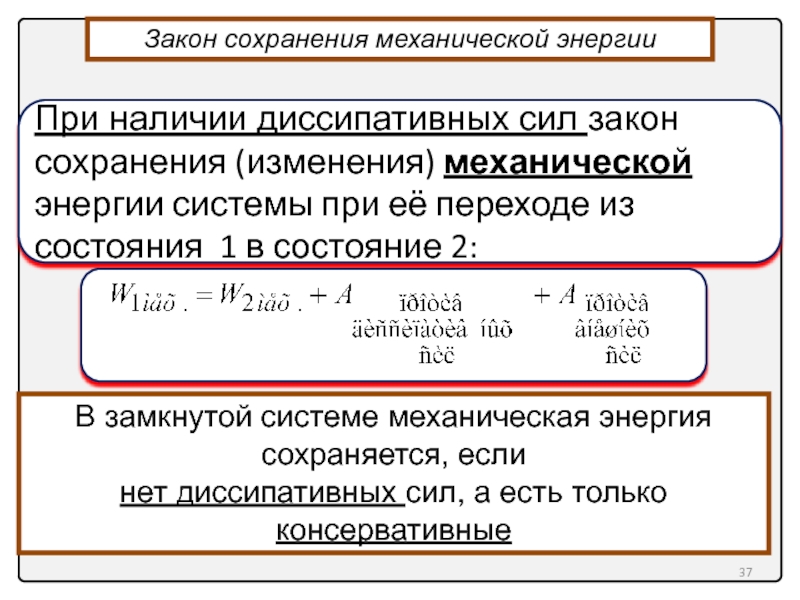
Слайд 37
В замкнутой системе механическая энергия сохраняется, если
нет диссипативных сил, а есть
При наличии диссипативных сил закон сохранения (изменения) механической энергии системы при её переходе из состояния 1 в состояние 2:
Закон сохранения механической энергии
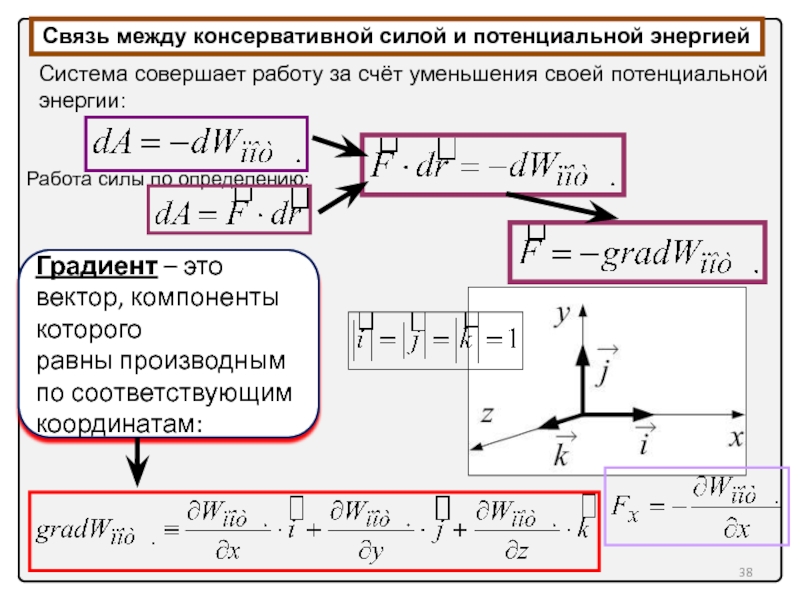
Слайд 38
Градиент – это вектор, компоненты которого
равны производным по соответствующим координатам:
Связь между
Система совершает работу за счёт уменьшения своей потенциальной энергии:
Работа силы по определению:
Слайд 39
Градиент показывает быстроту изменения величины в пространстве, направлен в сторону наибольшего
Сила направлена в сторону максимального убывания потенциальной энергии
Пример: одномерный случай
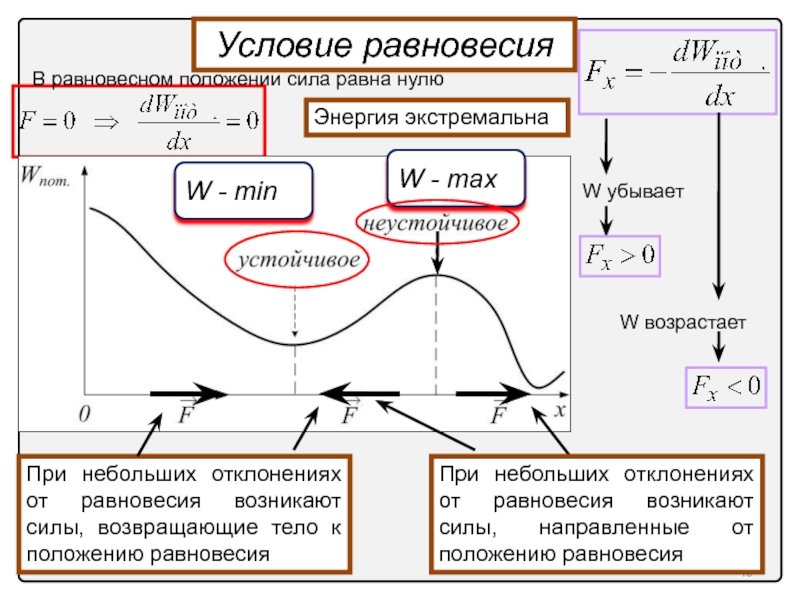
Слайд 40
Условие равновесия
В равновесном положении сила равна нулю
Энергия экстремальна
W - min
W -
При небольших отклонениях от равновесия возникают силы, возвращающие тело к положению равновесия
При небольших отклонениях от равновесия возникают силы, направленные от положению равновесия
W убывает
W возрастает