- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема о циркуляции вектора магнитной индукции. Ротор векторного поля презентация
Содержание
- 1. Теорема о циркуляции вектора магнитной индукции. Ротор векторного поля
- 2. Теорема о циркуляции вектора
- 3. Теорема о циркуляции в интегральной форме
- 5. В случае произвольного контура
- 6. Мы рассмотрели бесконечно малый контур. Можно записать:
- 7. Полевые уравнения.
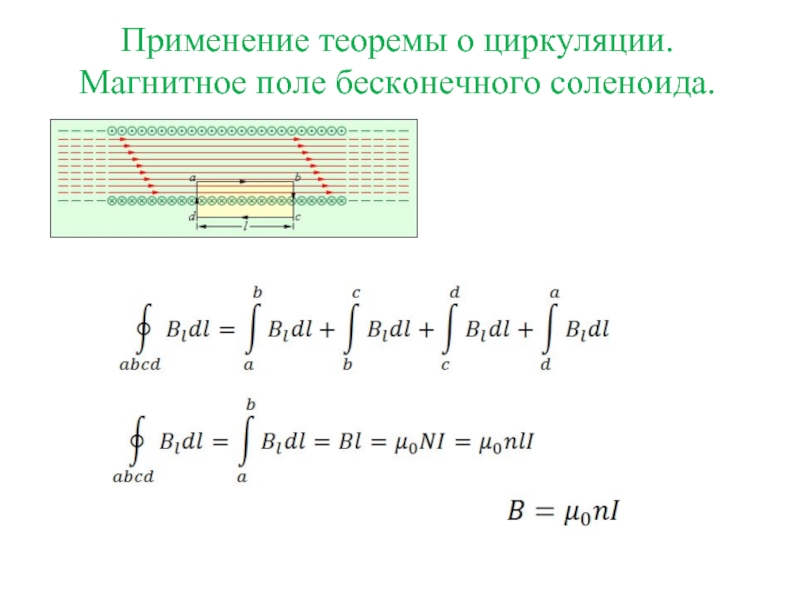
- 8. Применение теоремы о циркуляции. Магнитное поле бесконечного соленоида.
Теорема о циркуляции вектора Циркуляция вектора по произвольному контуру L равна произведению на алгебраическую сумму токов, охватываемых контуром L.
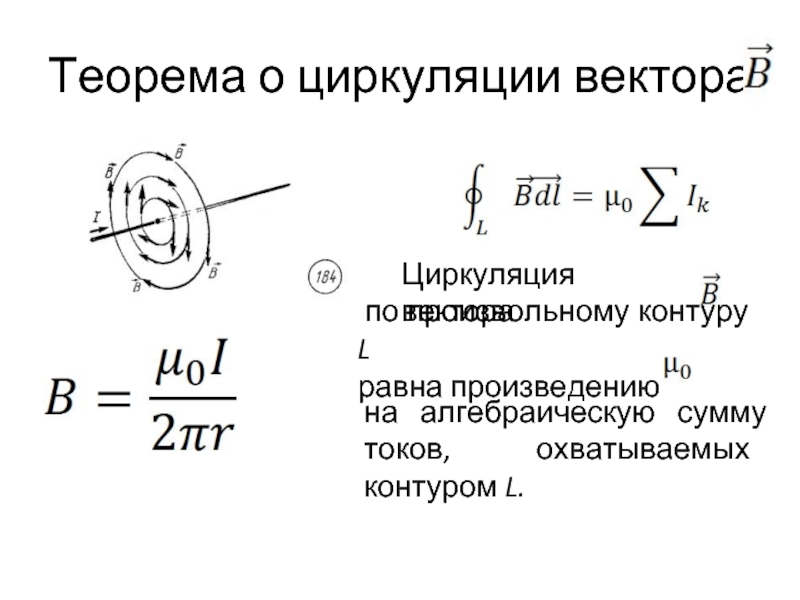
Слайд 2Теорема о циркуляции вектора
Циркуляция вектора
по произвольному контуру L
равна произведению
на алгебраическую сумму токов, охватываемых контуром L.
Слайд 3Теорема о циркуляции в интегральной форме
Перейдем к дифференциальной форме. Рассмотрим
плоский контур АВСD, находящийся в проводящей среде с плотностью тока , расположенный параллельно плоскости ZOY.
Обходим контур против часовой стрелки.
Слайд 6Мы рассмотрели бесконечно малый контур. Можно записать:
Предел – скалярная величина, которая
ведет себя как проекция некоторого вектора на направление нормали к плоскости контура, по которому берется циркуляция. Этот вектор – ротор поля. Предел зависит от ориентации контура в данной точке пространства. Направление нормали связано с направлением обхода правилом правого винта.
