- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Автоматика. Типовые звенья САУ и их свойства презентация
Содержание
- 1. Автоматика. Типовые звенья САУ и их свойства
- 2. Лекция 7-8. Типовые звенья САУ и их
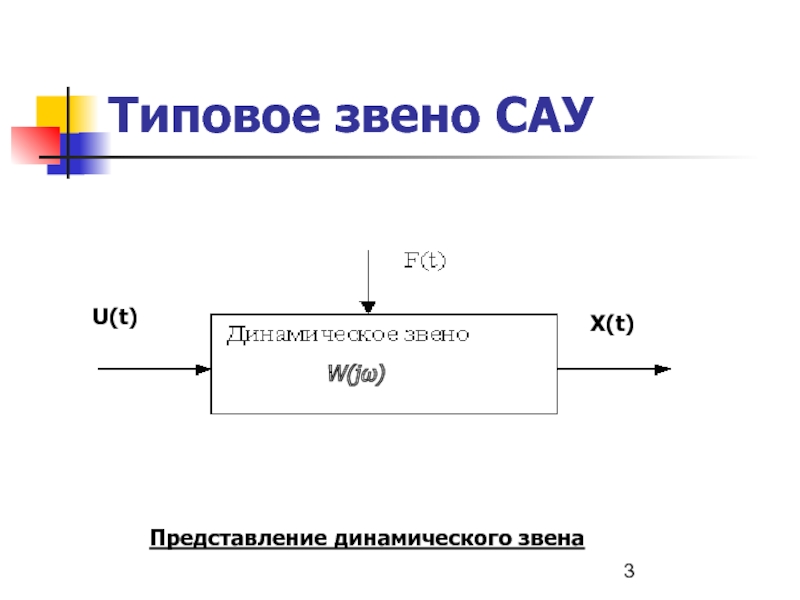
- 3. Типовое звено САУ Представление динамического звена W(jω) U(t) X(t)
- 4. Типовые звенья САУ Простейшими типовыми
- 5. Апериодическое звено Уравнение движения для апериодического
- 6. Апериодическое звено Выполняя над этим уравнением
- 7. Апериодическое звено Для нахождения временных характеристик
- 8. Апериодическое звено Выполняя обратное преобразование изображения
- 9. Апериодическое звено Временные
- 10. Апериодическое звено Амплитудно-частотная характеристика (АЧХ) апериодического
- 11. Апериодическое звено АФЧХ звена определяется как
- 12. Апериодическое звено Амплитудно-фазовая (АФХ)
- 13. Апериодическое звено Большинство тепловых
- 14. Интегрирующее звено Уравнение движения для интегрирующего
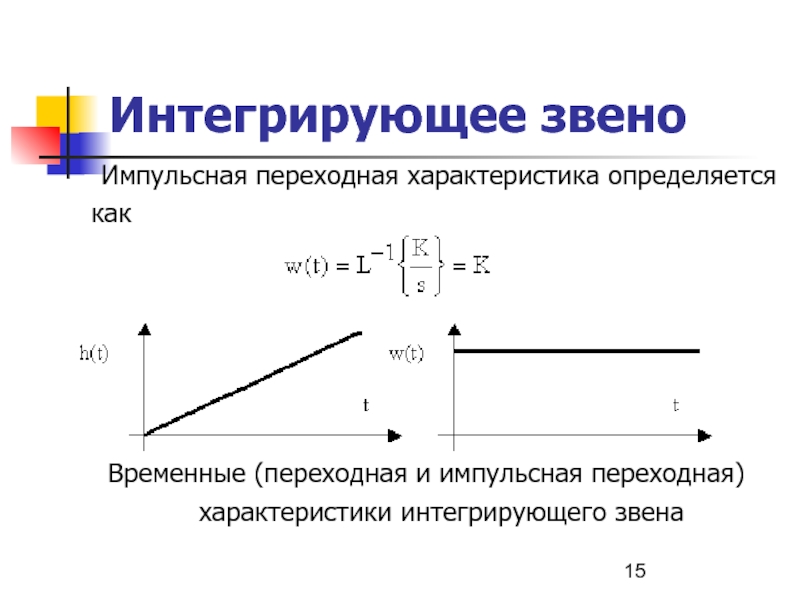
- 15. Интегрирующее звено Импульсная переходная характеристика определяется как
- 16. Интегрирующее звено Для построения частотных характеристик звена
- 17. Интегрирующее звено Выражение для расчета ЛАЧХ принимает
- 18. Интегрирующее звено При подаче на
- 19. Колебательное звено Уравнение движения для колебательного
- 20. Колебательное звено
- 21. Колебательное звено Для колебательного звена характерно
- 22. Колебательное звено Временные характеристики колебательного звена
- 23. Колебательное звено Для построения частотных
- 24. Колебательное звено Вещественная P(ω) и
- 25. Колебательное звено Для построения асимптотической
- 26. Дифференцирующее звено Уравнение движения для
- 27. Дифференцирующее звено Переходная характеристики дифференцирующего звена
- 28. Дифференцирующее звено Исходя из
- 29. Дифференцирующее звено АФХ ЛАЧХ
- 30. Дифференцирующее звено Идеальные
- 31. Усилительное (безинерционное) звено
- 32. Усилительное (безинерционное) звено
- 33. Усилительное (безинерционное) звено Логарифмическая частотная
- 34. Запаздывающее звено Уравнение движения звена имеет вид
Слайд 1АВТОМАТИКА
(2015-16)
Кафедра информационных систем
и технологий (ИСиТ)
Бейтюк Ю.Р.
заведующий кафедрой ИСиТ
к.т.н.,
Слайд 2Лекция 7-8. Типовые звенья САУ и их свойства
Типовые звенья САУ
Для
Звеном направленного действия называется звено, которое передает воздействие только в одном направлении - с "выхода" одного звена на "вход" другого, так, что изменение состояния первого звена не влияет на состояние предшествующего звена, работающего на его вход.
В результате при разбиении системы на звенья направленного действия, математическое описание каждого такого звена может быть составлено без учета его связей с другими звеньями.
Звенья систем регулирования могут иметь разную физическую основу (электрические, пневматические, механические и др. звенья), но относится к одной группе. Соотношения входных и выходных сигналов в звеньях одной группы описываются одинаковыми передаточными функциями.
Слайд 4Типовые звенья САУ
Простейшими типовыми звеньями являются:
апериодическое
колебательное
интегрирующее
усилительное
дифференцирующее
запаздывающее
Они описываются дифференциальными уравнениями не выше второго порядка.
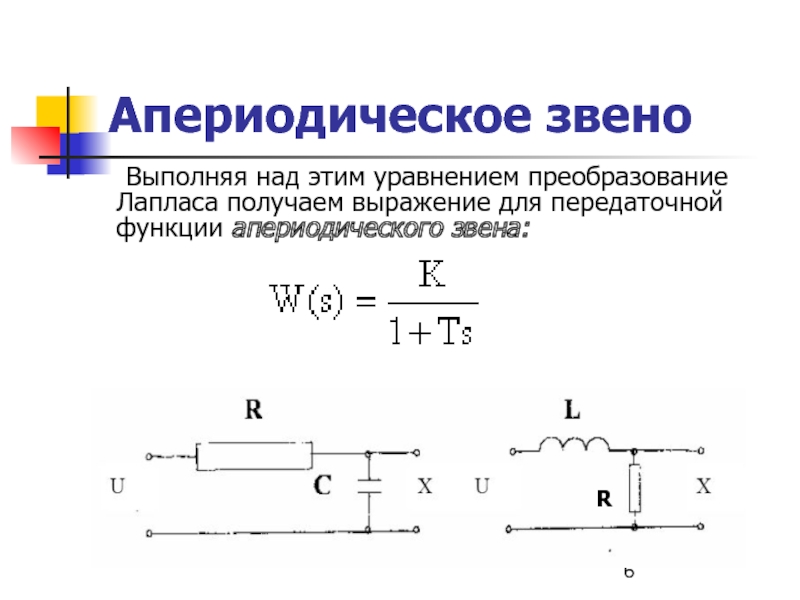
Слайд 5Апериодическое звено
Уравнение движения для апериодического звена имеет вид:
Т – постоянная
К – передаточный коэффициент
Х – выходная регулируемая величина
U – входное (управляющее) воздействие
t - время
Слайд 6Апериодическое звено
Выполняя над этим уравнением преобразование Лапласа получаем выражение для
R
Слайд 7Апериодическое звено
Для нахождения временных характеристик звена определим его реакцию на
Корни характеристического уравнения
определяются как
U
Слайд 8Апериодическое звено
Выполняя обратное преобразование изображения переходной характеристики
Выполняя аналогичные преобразования над изображением импульсной переходной функции получаем выражение для определения импульсной переходной функции
e –t/T
e –t/T
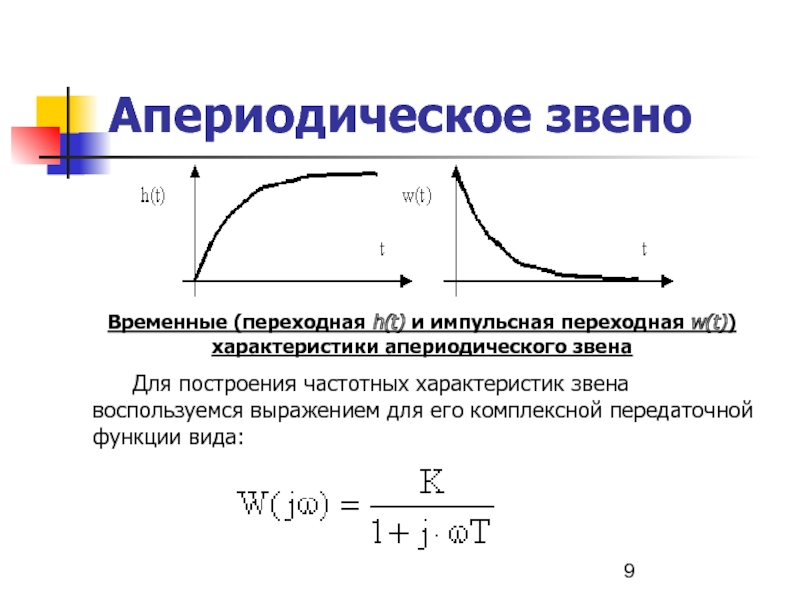
Слайд 9Апериодическое звено
Временные (переходная h(t) и импульсная переходная w(t)) характеристики
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функции вида:
Слайд 10Апериодическое звено
Амплитудно-частотная характеристика (АЧХ) апериодического звена определяется как:
Вещественная P(ω) и
Слайд 11Апериодическое звено
АФЧХ звена определяется как
Выражение для расчета ЛАЧХ и ЛФЧХ
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
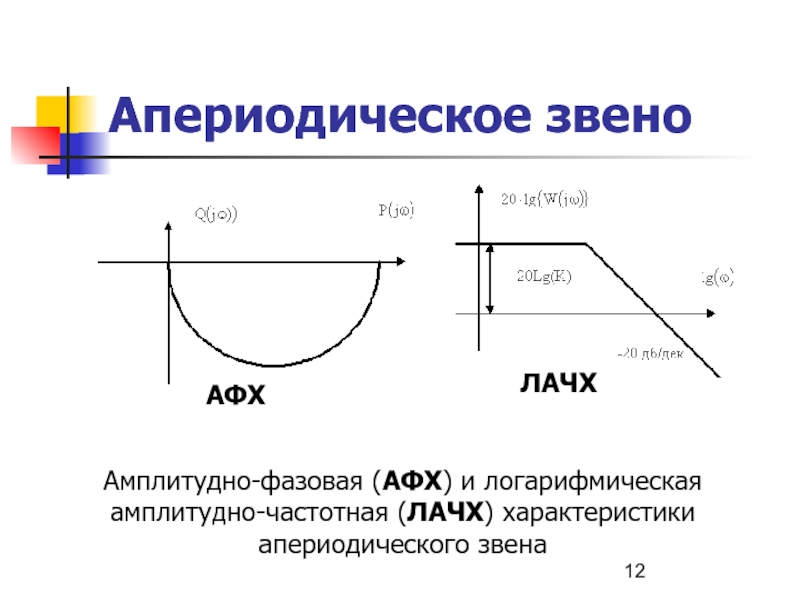
Слайд 12Апериодическое звено
Амплитудно-фазовая (АФХ) и логарифмическая амплитудно-частотная (ЛАЧХ) характеристики апериодического звена
АФХ
ЛАЧХ
Слайд 13Апериодическое звено
Большинство тепловых объектов являются апериодическими звеньями.
Например, при подаче
Примерами апериодических звеньев также являются исполнительные двигатели, усилители мощности, магнитные усилители и т.п.
Слайд 14
Интегрирующее звено
Уравнение движения для интегрирующего звена имеет вид
Выполняя над этим
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Переходная характеристика звена определяется как
Слайд 15Интегрирующее звено
Импульсная переходная характеристика определяется как
Временные (переходная и импульсная переходная) характеристики
Слайд 16Интегрирующее звено
Для построения частотных характеристик звена воспользуемся выражением для его комплексной
Исходя из этого, амплитудно-частотная характеристика звена определяется как:
Вещественная P(ω) и мнимая Q (ω) частотные характеристики звена определяются как
Слайд 17Интегрирующее звено
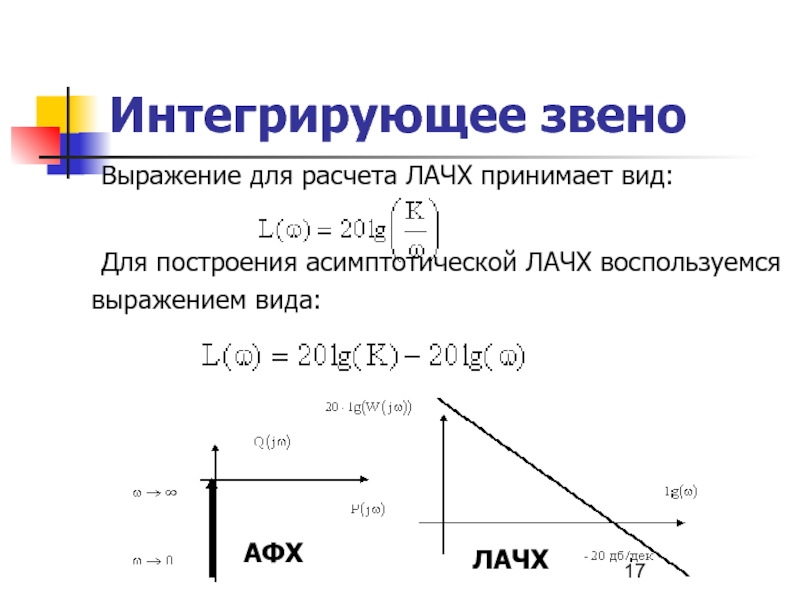
Выражение для расчета ЛАЧХ принимает вид:
Для построения асимптотической ЛАЧХ воспользуемся
АФХ
ЛАЧХ
Слайд 18Интегрирующее звено
При подаче на вход интегрирующего звена воздействия - выходной сигнал
Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением.
Слайд 19Колебательное звено
Уравнение движения для колебательного звена имеет вид
T - постоянная
- коэффициент демпфирования
Выполняя над этим уравнением преобразование Лапласа, получаем выражение для передаточной функции звена следующего вида:
Слайд 20Колебательное звено
Колебательное звено
Для нахождения временных характеристик звена определим его реакцию
1
Слайд 21Колебательное звено
Для колебательного звена характерно различное распределение корней при разных
— декремент затухания
— частота собственных колебаний
— начальная фаза колебаний
1
Слайд 22Колебательное звено
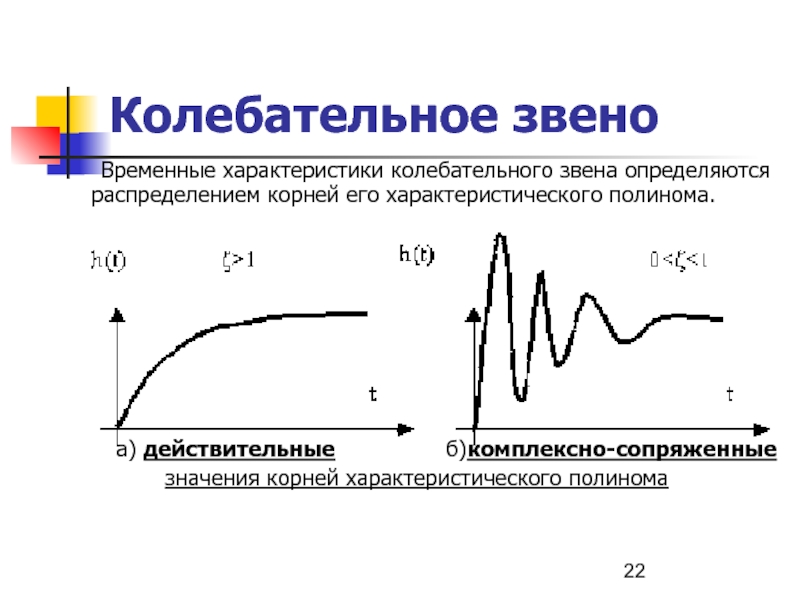
Временные характеристики колебательного звена определяются распределением корней его характеристического
а) действительные б)комплексно-сопряженные
значения корней характеристического полинома
Слайд 23Колебательное звено
Для построения частотных характеристик звена воспользуемся выражением для его
Исходя из этого, амплитудно-частотная характеристика колебательного звена определяется как:
Слайд 24Колебательное звено
Вещественная P(ω) и мнимая Q (ω) частотные характеристики звена
Выражение для расчета ЛАЧХ принимает вид:
Слайд 25Колебательное звено
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
»
АФХ
ЛАЧХ
Слайд 26
Дифференцирующее звено
Уравнение движения для дифференцирующего звена имеет вид
Выполняя над этим
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Переходная характеристика дифференцирующего звена определяется как
dU
X
Слайд 27Дифференцирующее звено
Переходная характеристики дифференцирующего звена
Для построения частотных характеристик звена
Слайд 28Дифференцирующее звено
Исходя из этого, амплитудно-частотная характеристика звена определяется
Вещественная P(ω) и мнимая Q (ω) частотные характеристики звена определяются как
Выражение для расчета ЛАЧХ принимает вид:
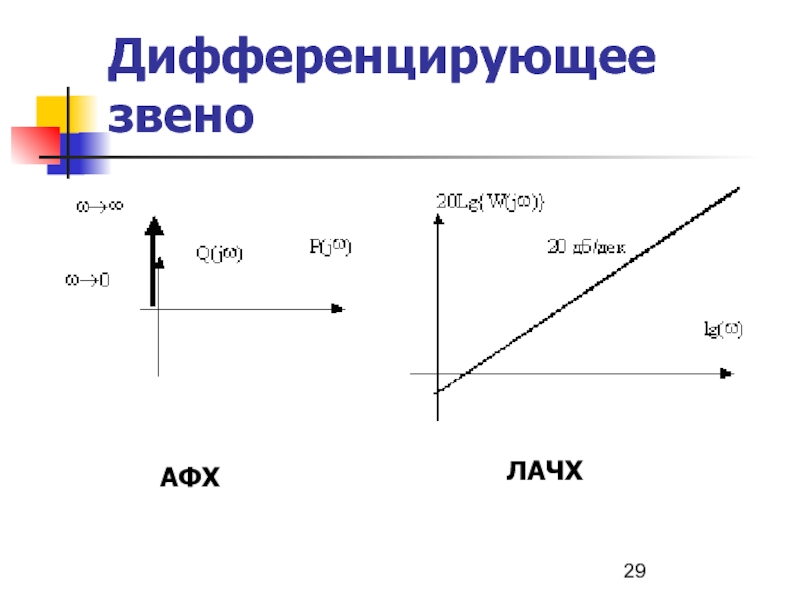
Для построения асимптотической ЛАЧХ воспользуемся выражением вида:
Слайд 30Дифференцирующее звено
Идеальные дифференцирующие звенья физически не реализуемы.
Передаточная функция реального дифференцирующего звена может иметь вид:
.
W(s)=
Слайд 31Усилительное (безинерционное) звено
Уравнение движения для усилительного звена
Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:
Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется как
Выполняя обратное преобразование изображения переходной характеристики, получаем:
U
Слайд 32Усилительное (безинерционное) звено
Выполняя аналогичные преобразования над изображением
Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функции вида:
Исходя из этого, амплитудно-частотная характеристика звена представляется точкой на комплексной плоскости.
Слайд 33Усилительное (безинерционное) звено
Логарифмическая частотная характеристика представляется прямой параллельной оси частот.
Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз.
Примерами таких звеньев являются: механические передачи, датчики, безинерционные усилители и др.
Слайд 34Запаздывающее звено
Уравнение движения звена имеет вид
X = U(t - τ0)
Передаточная
W(s) = e-τ0s
Выходная величина X в точности повторяет входную величину U с некоторым запаздыванием τ0.
Примером является конвейер.