- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы решения задач теплопроводности презентация
Содержание
- 1. Методы решения задач теплопроводности
- 2. Приближенные методы решения задач теплопроводности Точное
- 3. Приближенные методы решения задач теплопроводности Дифференциальное уравнение
- 4. Приближенные методы решения задач теплопроводности Наибольшее распространение
- 5. Метод элементарных тепловых балансов Тело разбивается на
- 6. Метод элементарных тепловых балансов Пусть температурное поле
- 7. Метод элементарных тепловых балансов Изменение внутренней энергии
- 8. Метод элементарных тепловых балансов Теплота к точке
- 9. Метод элементарных тепловых балансов С учетом (1),
- 10. Метод элементарных тепловых балансов
- 11. Метод элементарных тепловых балансов Уравнение (5) принимает
- 12. Метод элементарных тепловых балансов Из рассмотрения (7)
- 13. Метод элементарных тепловых балансов Частные случаи:
- 14. Метод элементарных тепловых балансов Пусть Пусть
- 15. Метод элементарных тепловых балансов Установлено, что устойчивость решения достигается лишь при
- 16. Метод элементарных тепловых балансов Аналогично можно получить решение для двухмерной задачи:
- 17. Метод элементарных тепловых балансов Установлено, что устойчивость решения достигается лишь при
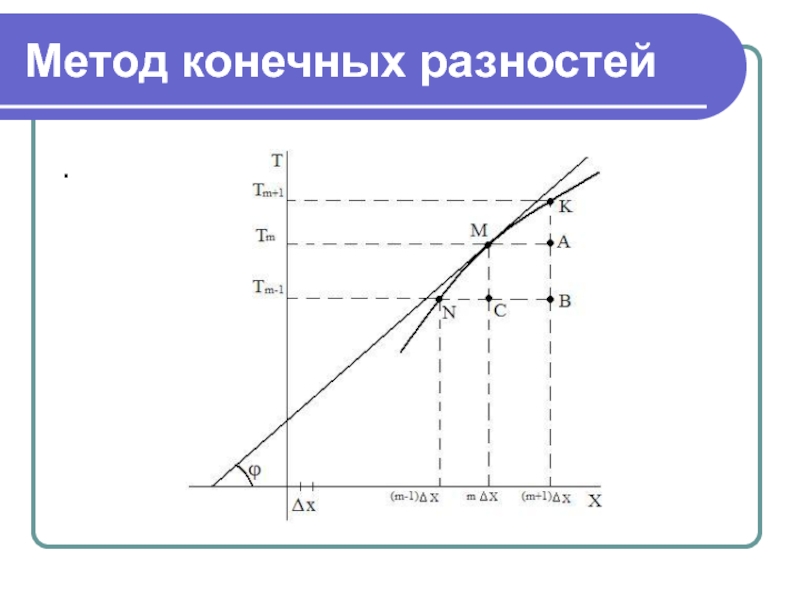
- 18. Метод конечных разностей В этом методе
- 19. Метод конечных разностей .
- 20. Метод конечных разностей Приближенные значения производных Предыдущие
- 21. Метод конечных разностей Симметричные значения производных:
- 22. Метод конечных разностей Вторая производная:
- 23. Метод конечных разностей Пусть температурное поле описывается
- 24. Метод конечных разностей Поскольку температура является функцией
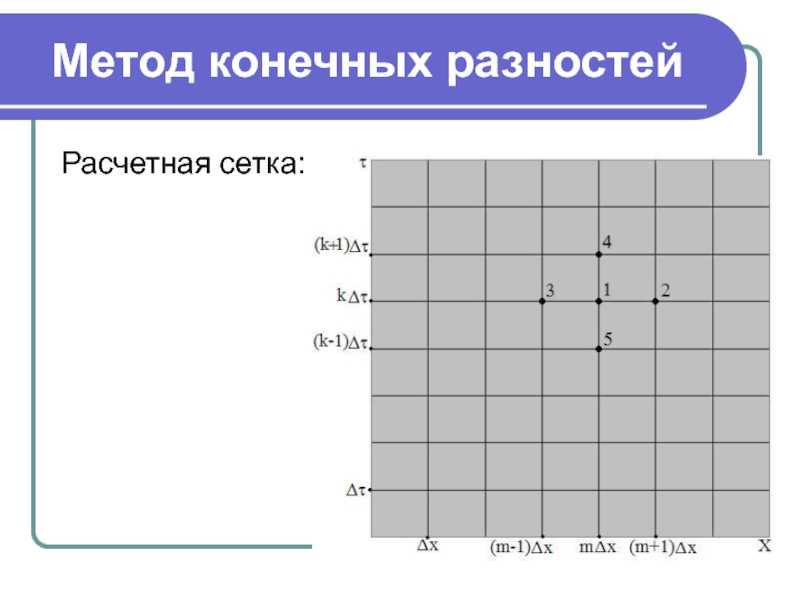
- 25. Метод конечных разностей Расчетная сетка:
- 26. Метод конечных разностей Координаты точек: 1:
- 27. Метод конечных разностей Заменим производные разностными соотношениями:
- 28. Метод конечных разностей Формула (1) примет вид:
- 29. Метод конечных разностей Или:
- 30. Метод конечных разностей Уравнение (2) составляется для
- 31. Метод конечных разностей Пусть температурное поле описывается
- 32. Метод конечных разностей Заменим производные разностными соотношениями:
- 33. Метод конечных разностей Уравнение (3) примет вид:
- 34. Метод конечных разностей Пусть
- 35. Метод конечных разностей Обозначают числа Фурье: Часто принимают
- 36. Метод конечных разностей Тогда формула примет вид:
- 37. Метод конечных разностей Устойчивость решения обеспечивается при условии:
- 38. Вопросы к экзамену Метод элементарных тепловых балансов. Метод конечных разностей.
Приближенные методы решения задач теплопроводности Точное аналитическое решение позволяет рассчитать температуру в любой точке тела, однако, не любую задачу теплопроводности можно решить аналитически. В том случае, когда тело имеет сложную
Слайд 2Приближенные методы решения задач теплопроводности
Точное аналитическое решение позволяет рассчитать температуру
в любой точке тела, однако, не любую задачу теплопроводности можно решить аналитически. В том случае, когда тело имеет сложную форму и коэффициент теплоотдачи является величиной переменной, задачу по теплообмену аналитически решить невозможно. В этом случае используют приближенные методы решения задач (численные методы).
Слайд 3Приближенные методы решения задач теплопроводности
Дифференциальное уравнение теплопроводности заменяется системой алгебраических уравнений.
Температура рассчитывается в отдельных фиксированных точках тела, точность расчета зависит от выбранного шага разбиения тела на отдельные участки.
Слайд 4Приближенные методы решения задач теплопроводности
Наибольшее распространение получили два метода расчета:
Метод элементарных
тепловых балансов.
Метод конечных разностей.
Метод конечных разностей.
Слайд 5Метод элементарных тепловых балансов
Тело разбивается на отдельные объемы.
Центральным точкам каждого
объема присваивается отдельный номер.
Эти точки обладают определенной массой и теплоемкостью.
К каждой точке теплота подводится или отводится через стержни, с помощью которых точки условно соединены друг с другом.
При этом внутренняя энергия точки может увеличиваться или уменьшаться.
Эти точки обладают определенной массой и теплоемкостью.
К каждой точке теплота подводится или отводится через стержни, с помощью которых точки условно соединены друг с другом.
При этом внутренняя энергия точки может увеличиваться или уменьшаться.
Слайд 6Метод элементарных тепловых балансов
Пусть температурное поле описывается уравнением:
Разбиваем стенку на элементарные
объемы:
Слайд 7Метод элементарных тепловых балансов
Изменение внутренней энергии в рассматриваемой узловой точке:
(1)
- удельная массовая теплоемкость;
- плотность;
- начальная температура точки 0;
- температура этой точки через время
- удельная массовая теплоемкость;
- плотность;
- начальная температура точки 0;
- температура этой точки через время
Слайд 8Метод элементарных тепловых балансов
Теплота к точке 0 подводится от точки 1
и точки 2 за счет теплопроводности:
(2)
(3)
Уравнение теплового баланса:
(4)
(2)
(3)
Уравнение теплового баланса:
(4)
Слайд 10Метод элементарных тепловых балансов
- коэффициент температуропроводности.
- критерий Фурье.
При фиксированном значении шага разбиения по пространству и по времени критерий Фурье является величиной постоянной .
Слайд 12Метод элементарных тепловых балансов
Из рассмотрения (7) следует, что будущая температура в
рассматриваемой точке является функцией настоящей температуры в этой точке и настоящих температур в соседних точках.
Слайд 13Метод элементарных тепловых балансов
Частные случаи:
Пусть
Будущая температура в рассматриваемой точке не зависит
от настоящей температуры в этой точке.
Слайд 15Метод элементарных тепловых балансов
Установлено, что устойчивость решения достигается лишь при
Слайд 16Метод элементарных тепловых балансов
Аналогично можно получить решение для двухмерной задачи:
Слайд 17Метод элементарных тепловых балансов
Установлено, что устойчивость решения достигается лишь при
Слайд 18Метод конечных разностей
В этом методе производные, входящие в дифференциальное уравнение
теплопроводности, замещаются разностными соотношениями:
Слайд 20Метод конечных разностей
Приближенные значения производных
Предыдущие значения производных:
Последующие значения производных:
Слайд 23Метод конечных разностей
Пусть температурное поле описывается дифференциальным уравнением:
(1)
Слайд 24Метод конечных разностей
Поскольку температура является функцией двух переменных, удобно выбрать прямоугольную
сетку. Интервал изменения разделим на одинаковые интервалы , а отрезок времени разделим на равномерные интервалы Восстановленные перпендикуляры к координатным осям в точках деления при пересечении образуют расчетные узловые точки.
Слайд 30Метод конечных разностей
Уравнение (2) составляется для каждой узловой точки включая пограничные
точки.
Погрешность расчета уменьшается при .
Устойчивость решения обеспечивается лишь при условии:
Погрешность расчета уменьшается при .
Устойчивость решения обеспечивается лишь при условии:
Слайд 31Метод конечных разностей
Пусть температурное поле описывается дифференциальным уравнением вида:
(3)
