ТЕМА: ВИЗНАЧЕННЯ ВАРТОСТІ ГРОШЕЙ У ЧАСІ ТА ЇЇ
ВИКОРИСТАННЯ У ФІНАНСОВИХ РОЗРАХУНКАХ
ПЛАН
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Визначення вартості грошей у часі та її використання у фінансових розрахунках презентация
Содержание
- 1. Визначення вартості грошей у часі та її використання у фінансових розрахунках
- 2. Концепція вартості грошей у часі: гроші сьогодні
- 3. . Процент- це грошова плата, стягнута або
- 4. Попередній метод нарахування відсотка (метод пренумерандо або
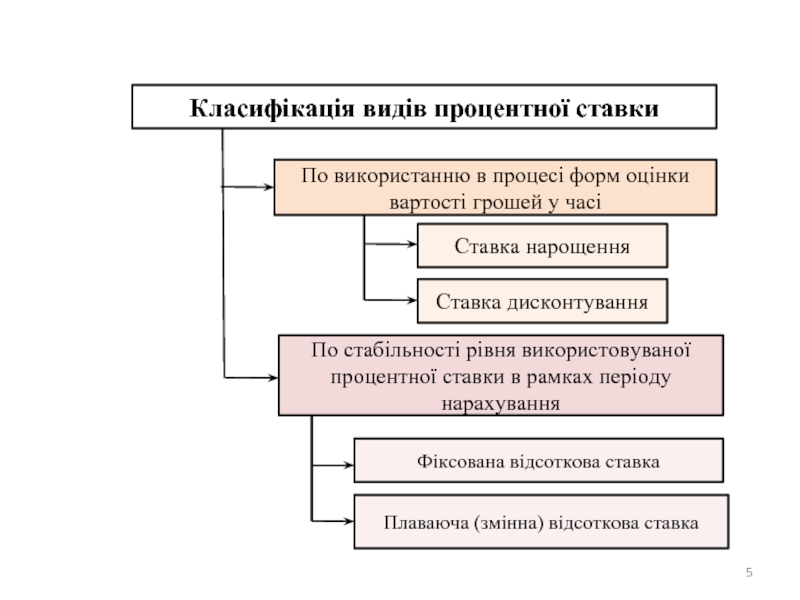
- 6. СХЕМА ПРОСТИХ ПРОЦЕНТІВ В ПРОЦЕСІ НАРОЩЕННЯ ВАРТОСТІ
- 7. САМОСТІЙНО: Завдання 1. Необхідно визначити суму
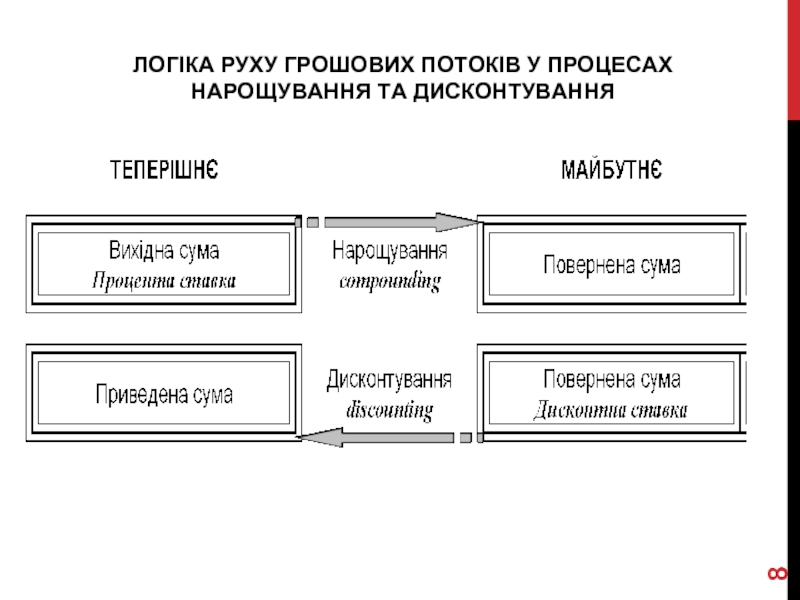
- 8. ЛОГІКА РУХУ ГРОШОВИХ ПОТОКІВ У ПРОЦЕСАХ НАРОЩУВАННЯ ТА ДИСКОНТУВАННЯ
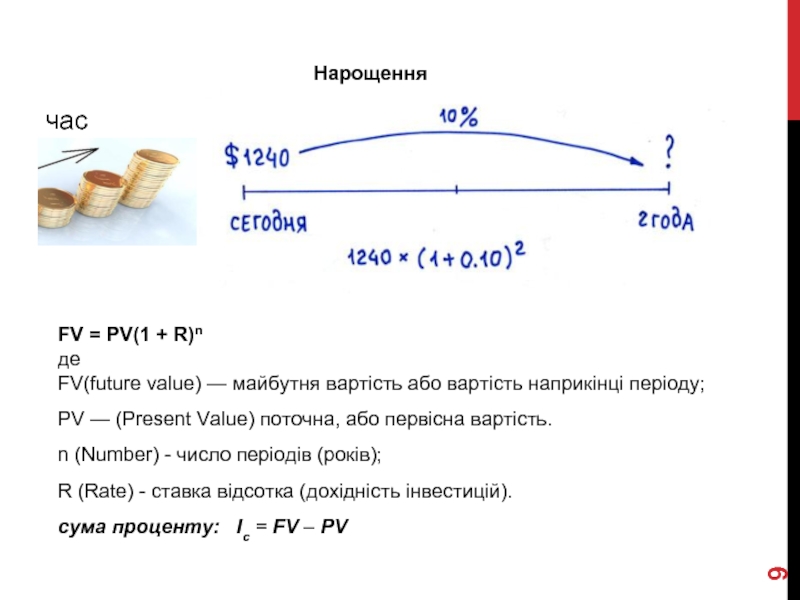
- 9. Нарощення FV = PV(1 + R)n
- 10. Приклад, підприємство поклало 30 000 грн. на
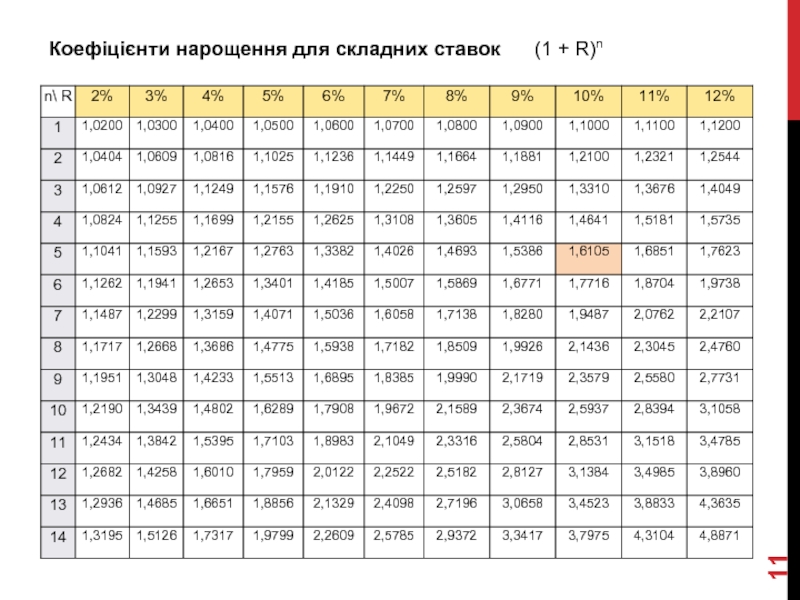
- 11. Коефіцієнти нарощення для складних ставок (1 + R)n
- 12.
- 13. Дисконтування
- 14. САМОСТІЙНО: Вихідні дані: 35000 доларів -
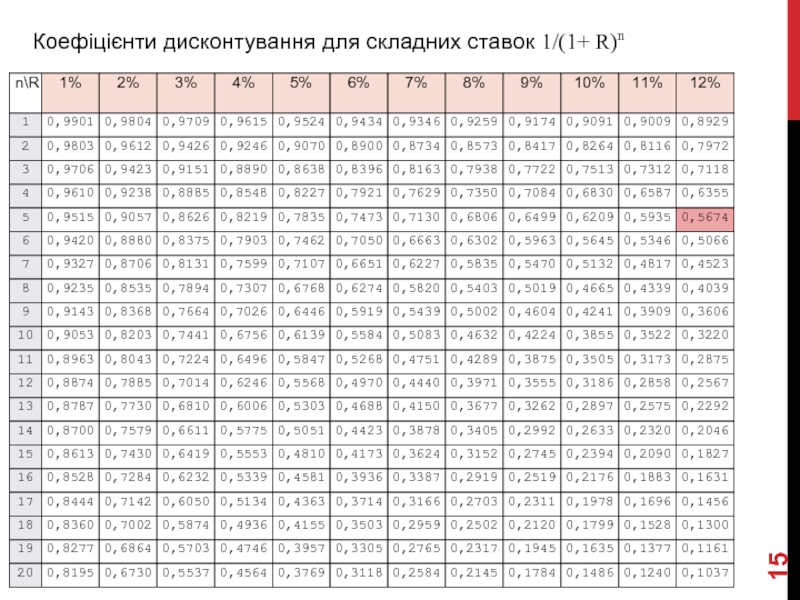
- 15. Коефіцієнти дисконтування для складних ставок 1/(1+ R)n
- 16. Чиста приведена вартість проекту – значення
- 17. де: NPV (Net Present Value) —
- 18. САМОСТІЙНО: Підприємству запропоновано інвестувати 25 млн
- 19. Ануїтет – тривалий потік платежів, що характеризується
- 20. Вибрати, що краще: (А)
- 21. Чиста приведена вартість характеризує загальний абсолютний результат
- 23. Приклад: 1500 доларов – це сума платежу
Слайд 1 1. КОНЦЕПЦІЯ ВАРТОСТІ ГРОШЕЙ У ЧАСІ 2. НАРАХУВАННЯ ПРОСТИХ І СКЛАДНИХ ВІДСОТКІВ. 3.
Слайд 2Концепція вартості грошей у часі: гроші сьогодні коштують більше, ніж така
Майбутня вартість грошей являє собою суму інвестованих у даний момент коштів, в яку вони перетворяться через певний період часу з урахуванням певної ставки відсотка (процентної ставки).
Компаундинг — (англ. compounding ) зростання у часі вкладеної грошової суми в результаті реінвестування одержуваних на неї відсотків.
Теперішня вартість грошей являє собою суму майбутніх грошових засобів, приведеної з урахуванням певної ставки процента до теперішнього періоду часу.
Дисконтування - це процес визначення сьогоднішньої (поточної) вартості грошей, коли відома їх майбутня вартість.
Слайд 3.
Процент- це грошова плата, стягнута або виплачувана за використання грошей.
Прості проценти
Складні проценти - це проценти, нараховані на вже виплачені проценти, а також на основну суму, взяту (віддану) у борг.
Процентна ставка (ставка відсотка) — питомий показник, згідно з яким у встановлені строки виплачується сума відсотка в розрахунку на одиницю грошового капіталу.
Слайд 4Попередній метод нарахування відсотка (метод пренумерандо або антисипативный метод) характеризує спосіб
Наступний метод нарахування відсотка (метод постнумерандо або декурсивный метод) характеризує спосіб платежів, при якому нарахування відсотка здійснюється в кінці кожного інтервалу.
Дискретний грошовий потік, характеризує потік платежів на вкладений грошовий капітал, який має чітко детермінований період нарахування відсотків і кінцевий термін повернення основної його суми.
Безперервний грошовий потік характеризує потік платежів на вкладений грошовий капітал, період нарахування відсотків за якого не обмежений і не визначено кінцевий термін повернення основної його суми.
Ануїтет (фінансова рента) — тривалий потік платежів, що характеризується однаковим рівнем процентних ставок в кожному з інтервалів розглянутого періоду часу.
Слайд 6СХЕМА ПРОСТИХ ПРОЦЕНТІВ В ПРОЦЕСІ НАРОЩЕННЯ ВАРТОСТІ
FV = PV × (1
FV − майбутня вартість грошей;
PV − теперішня вартість грошей;
R − потрібна норма дохідності (процентна ставка або нав’язана вартість грошей) в долях одиниці;
n − кількість років, протягом яких здійснюється нарощування грошей.
СХЕМА ПРОСТИХ ПРОЦЕНТІВ В ПРОЦЕСІ ДИСКОНТУВАННЯ ВАРТОСТІ
Слайд 7САМОСТІЙНО:
Завдання 1. Необхідно визначити суму простого відсотку за рік при наступних
первинна сума внеску — 1000 умов. грош. од.;
процентна ставка, що виплачується щокварталу -20%.
Завдання 2. Необхідно визначити суму дисконту за простим відсотком за рік при наступних умовах:
кінцева сума внеску визначена в розмірі 1000 умов. грош. од.;
дисконтна ставка становить 20% у квартал.
Слайд 9Нарощення
FV = PV(1 + R)n
де
FV(future value) — майбутня вартість або вартість наприкінці періоду;
PV — (Present Value) поточна, або первісна вартість.
n (Number) - число періодів (років); R (Rate) - ставка відсотка (дохідність інвестицій).
сума проценту: Іс = FV – PV
час
Слайд 10Приклад, підприємство поклало 30 000 грн. на депозит у банк під
33 000 = 30 000 × (1+0,10)1
Тобто сума процента (дохід) за рік буде дорівнює 3000 гривень.
Іс = FV – PV, 3000 = 33000 – 30000
САМОСТІЙНО:
Розрахувати суму депозиту, яку матиме підприємство через 5 років
Слайд 14САМОСТІЙНО:
Вихідні дані: 35000 доларів - це сума платежу (грошового відтоку);
R –
n – 5 років
ВИЗНАЧИТИ: скільки буде коштувати сьогодні сума грошей, яку ви чи отримаєте, або плануєте витратити в майбутньому через 5 років?
Слайд 16
Чиста приведена вартість проекту – значення чистого потоку грошових коштів за
Чиста приведена вартість характеризує загальний абсолютний результат інвестиційного проекту.
Слайд 17
де:
NPV (Net Present Value) — чиста приведена (до сьогоднішнього дня) вартість;
n,
CF — грошовий потік (Cash Flow),
R — вартість капіталу (ставка дисконтування, Rate),
It — інвестиційні витрати в період t
У випадку, якщо інвестиційні витрати здійснюються протягом ряду років, формула розрахунку прийме наступний вигляд:
Слайд 18САМОСТІЙНО:
Підприємству запропоновано інвестувати 25 млн грн. на термін три роки в
Слайд 19Ануїтет – тривалий потік платежів, що характеризується однаковим рівнем процентних ставок
Слайд 20Вибрати, що краще:
(А) отримати 100 доларів сьогодні або
(Б)
Формула ануїтету (для розрахунку дисконтованої вартості ануїтетних грошових потоків)
PV = FV × [1/(1+R)1 + 1/(1+R)2 + 1/(1+R)3 + 1/(1+R)4 +1/(1+R)5]
Слайд 21Чиста приведена вартість характеризує загальний абсолютний результат інвестиційного проекту.
Її визначають як
Слайд 23Приклад: 1500 доларов – це сума платежу (грошового відтоку);
R – 10%
n – 2 роки
PV= 1500× 1/(1+0,1)2 = 1500 × 1 / 1,21= 1240 $
або
1500× 0,8264 = 1240 $ (поточна вартість)
Дисконтована вартість - це поточна вартість майбутнього грошового потоку.