многомерных копула-функций
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Анализ состояния фондового рынка на основе многомерных копула-функций презентация
Содержание
- 1. Анализ состояния фондового рынка на основе многомерных копула-функций
- 2. Цель и задачи Целью работы является исследование
- 3. Копула (лат. Copula-пара) — это функция многомерного распределения, определённая на n-мерном единичном
- 4. Независимая копула-функция: С┴(u1…un)= u1*…*un. Комонотонная копула-функция: Cmax(u1…un)=min{u1…un}. Эталонные копула-фунции
- 5. Берется временной ряд цен акций компании, а
- 6. 3. Вычисляются расстояния до эталонной копула-функции C*
- 7. Исходные данные Таблица 1. Список акций анализируемых компаний
- 8. Применение аппарата копула-функций для исследования акций Google
- 9. t2 t2 Расст. до Cmax Рисунок
- 10. t2 t2 Расст. до С┴ Рисунок
- 11. Таблица 3. АКФ за 2008г. Таблица 4.
- 12. Произведена оценка характера связи внутри временного ряда
- 13. А. И. Авзалова, М.В. Филиппова. Исследование динамики
- 14. Спасибо за внимание!
- 15. Результаты исследования Иностранный IT сектор
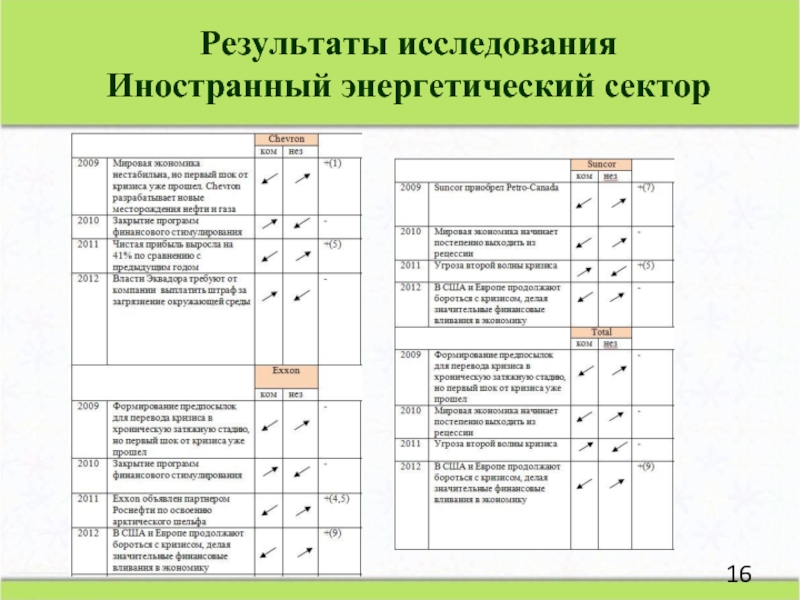
- 16. Результаты исследования Иностранный энергетический сектор
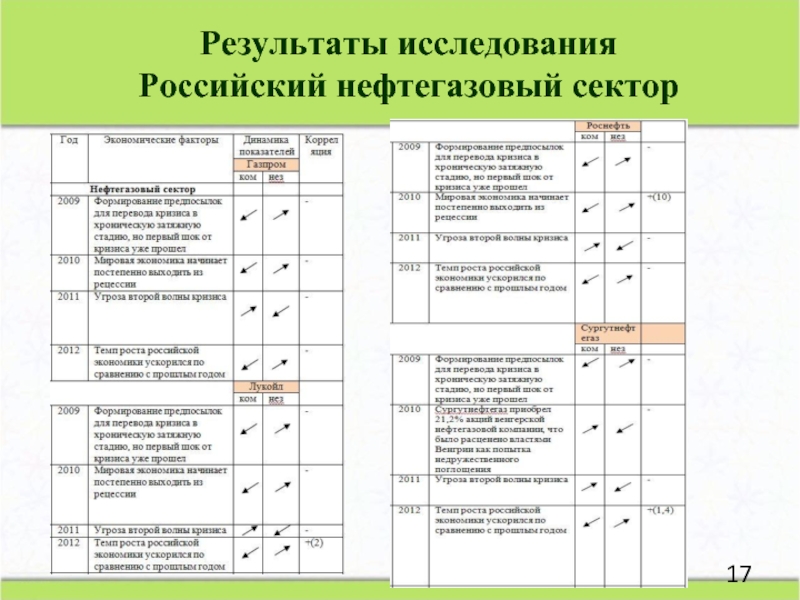
- 17. Результаты исследования Российский нефтегазовый сектор
- 18. Результаты исследования Российский энергетический сектор
Цель и задачи Целью работы является исследование внутренней зависимости во временных рядах цен акций с помощью копула- и автокорреляционных функций. Задачи: Разработка методики применения многомерных копула-функций к анализу временных рядов курсов
Слайд 1Выполнила:
Научный руководитель:
д.ф.-м.наук Бронштейн Е.М.
Анализ состояния фондового рынка на основе
Слайд 2Цель и задачи
Целью работы является исследование внутренней зависимости во временных рядах
цен акций с помощью копула- и автокорреляционных функций.
Задачи:
Разработка методики применения многомерных копула-функций к анализу временных рядов курсов акций;
Построение статистических оценок трехмерных копула-функций и определение на их основе типа связи во временных рядах;
Построение автокорреляционных функций временных рядов;
Анализ результатов, полученных с помощью копула- и автокорреляционных функций.
Задачи:
Разработка методики применения многомерных копула-функций к анализу временных рядов курсов акций;
Построение статистических оценок трехмерных копула-функций и определение на их основе типа связи во временных рядах;
Построение автокорреляционных функций временных рядов;
Анализ результатов, полученных с помощью копула- и автокорреляционных функций.
Слайд 3Копула (лат. Copula-пара) — это функция многомерного распределения, определённая на n-мерном единичном кубе [0,1]n, такая, что
каждое её маргинальное распределение равномерно на интервале [0,1].
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятыми со сдвигом по времени.
Автокорреляционная функция (АКФ) определяется интегралом:
и показывает связь функции с копией самой себя, смещенной на величину .
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятыми со сдвигом по времени.
Автокорреляционная функция (АКФ) определяется интегралом:
и показывает связь функции с копией самой себя, смещенной на величину .
Основные определения
Слайд 4 Независимая копула-функция:
С┴(u1…un)= u1*…*un.
Комонотонная копула-функция:
Cmax(u1…un)=min{u1…un}.
Эталонные копула-фунции
Слайд 5Берется временной ряд цен акций компании, а также два ряда, полученные
из исходного с помощью сдвига на величины t1 и t2, находящиеся в промежутке от 1 до 10, причём t1 < t2.
Строится статистическая оценка трёхмерной копула-функции на решётке с шагом 1/N.
Дано:
- результаты наблюдений, где u0 - исходный временной ряд,
u1 и u2 -временные ряды, сдвинутые относительно исходного на величины t1 и t2,
n – число наблюдений (причем n>>N),
u0(i), u1(j) , u2(g) - соответствующие порядковые статистики,
n(i,j,g)/n – оценка значения копула-функции ,
где n(i,j,g) – число троек выборки ,
для которого выполняются неравенства:
Строится статистическая оценка трёхмерной копула-функции на решётке с шагом 1/N.
Дано:
- результаты наблюдений, где u0 - исходный временной ряд,
u1 и u2 -временные ряды, сдвинутые относительно исходного на величины t1 и t2,
n – число наблюдений (причем n>>N),
u0(i), u1(j) , u2(g) - соответствующие порядковые статистики,
n(i,j,g)/n – оценка значения копула-функции ,
где n(i,j,g) – число троек выборки ,
для которого выполняются неравенства:
Этапы исследования
Слайд 6
3. Вычисляются расстояния до эталонной копула-функции C* , в качестве которой поочередно
используются С┴ и Cmax. Расчет производится по формуле:
Строятся автокорреляционные функции:
Проводится сравнительный анализ расчётов, полученных с помощью копула- и автокорреляционных функций.
Строятся автокорреляционные функции:
Проводится сравнительный анализ расчётов, полученных с помощью копула- и автокорреляционных функций.
Этапы исследования
Слайд 8Применение аппарата копула-функций для исследования акций Google Inc.
Таблицы 2. Суммы отклонений
статистических оценок копула-функций от эталонных за 2008-2012гг
Таблица 3. Динамика связей в ряду данных в зависимости от макроэкономических факторов за 2008-2012гг
t2
t1
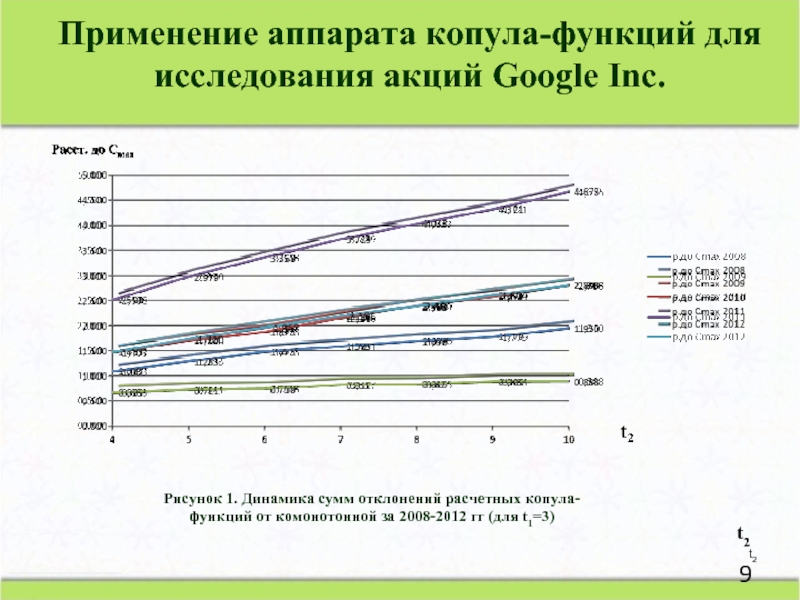
Слайд 9t2
t2
Расст. до Cmax
Рисунок 1. Динамика сумм отклонений расчетных копула-функций от
комонотонной за 2008-2012 гг (для t1=3)
Применение аппарата копула-функций для исследования акций Google Inc.
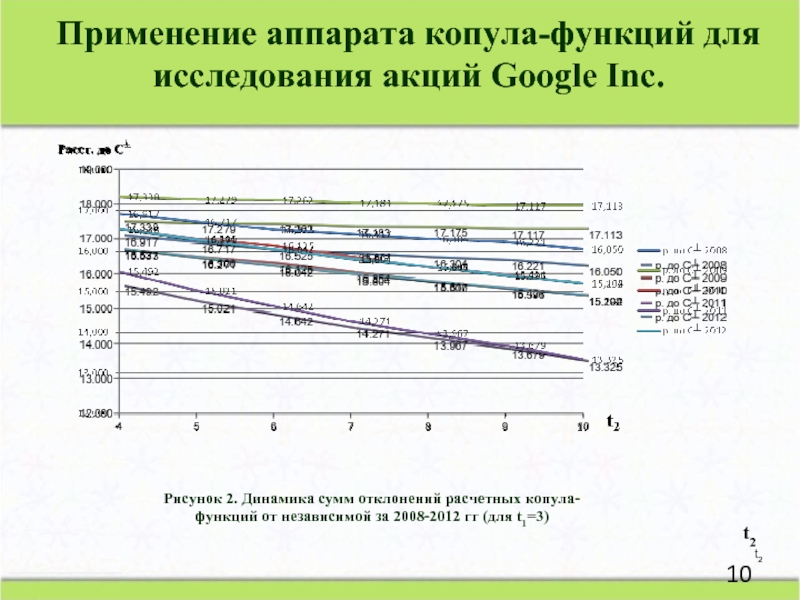
Слайд 10t2
t2
Расст. до С┴
Рисунок 2. Динамика сумм отклонений расчетных копула-функций от
независимой за 2008-2012 гг (для t1=3)
Применение аппарата копула-функций для исследования акций Google Inc.
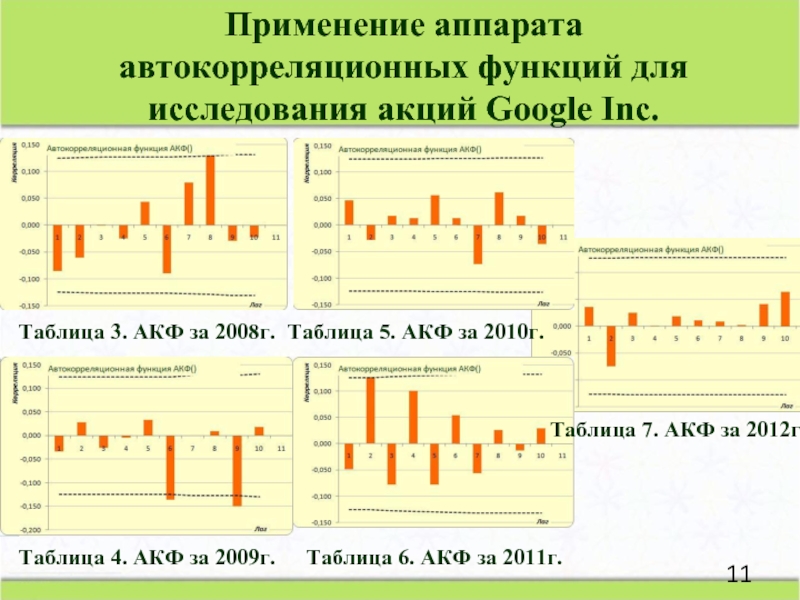
Слайд 11Таблица 3. АКФ за 2008г.
Таблица 4. АКФ за 2009г.
Таблица 5. АКФ
за 2010г.
Таблица 6. АКФ за 2011г.
Таблица 7. АКФ за 2012г.
Применение аппарата автокорреляционных функций для исследования акций Google Inc.
Слайд 12 Произведена оценка характера связи внутри временного ряда в зависимости от величины
временных лагов с использованием копула-функций.
Было выявлено, что:
Комонотонная связь внутри ряда выражена сильнее, чем независимая.
Во время экономического подъёма во временном ряду усиливается независимость, а во время экономического спада – комонотонная связь между наблюдениями.
При увеличении комонотонной связи разброс расстояний до эталонных копула-функций при увеличении временных лагов уменьшается, то есть прогноз цены акции становится более обоснованным.
Были построены автокорреляционные функции и произведено сравнение результатов, полученных с помощью копула- и автокорреляционных функций.
Было выявлено, что:
Комонотонная связь внутри ряда выражена сильнее, чем независимая.
Во время экономического подъёма во временном ряду усиливается независимость, а во время экономического спада – комонотонная связь между наблюдениями.
При увеличении комонотонной связи разброс расстояний до эталонных копула-функций при увеличении временных лагов уменьшается, то есть прогноз цены акции становится более обоснованным.
Были построены автокорреляционные функции и произведено сравнение результатов, полученных с помощью копула- и автокорреляционных функций.
Выводы
Слайд 13А. И. Авзалова, М.В. Филиппова. Исследование динамики цен акций с помощью
копула-функций.
Молодой ученый:
ежемесячный научный журнал.
Том 2 №5(40)/2012.
Чита: ООО Молодой ученый.
С. 232-238
Молодой ученый:
ежемесячный научный журнал.
Том 2 №5(40)/2012.
Чита: ООО Молодой ученый.
С. 232-238
