- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производственная функция презентация
Содержание
- 1. Производственная функция
- 2. Для рассмотрения производственной функции необходимо иметь в
- 3. Повышение уровня выпуска ВВП может быть достигнуто:
- 4. Таким образом, выпуск производимых в экономике товаров
- 5. Допустим также, что увеличение числа рабочих и
- 6. Согласно системе национальных счетов, ВВП равен сумме
- 7. Согласно теории функции потребления: c+s = 1,
- 8. Подставляя в равенство ΔQ = ΔC+ ΔI
- 9. Это равенство говорит о том, что при
- 10. Теперь рассмотрим производственную функцию xQ = f(xL,
- 11. Δ Q = ΔQL+ΔQK. Теперь темп прироста
- 12. Разумеется, 0 ≤ а ≤1. Предположим,
- 13. (5/50*0,6)*100 = 6 (5/55*0,6)*100 = 5,45 При
- 14. Экономический рост сопровождается тем, что при прежнем
- 15. Если совокупная факторная производительность растет, то выпуск
- 16. Рост совокупной факторной производительности может быть выражен
Слайд 2Для рассмотрения производственной функции необходимо иметь в виду:
в качестве показателя выпуска
будет служить ВВП, национальный доход или другой показатель объема всего национального производства (труд - общее число занятых в экономике).
объем ВВП может быть увеличен и за счет привлечения дополнительного количества занятых, и за счет увеличения размеров применяемого в экономике капитала.
необходимо использовать среднегодовой темп прироста ВВП, НД и т.д. за рассматриваемый период.
ресурсы, которыми располагает экономика, используются с полной загрузкой, т. е. имеет место полная занятость и оптимальная загрузка производственных мощностей.
объем ВВП может быть увеличен и за счет привлечения дополнительного количества занятых, и за счет увеличения размеров применяемого в экономике капитала.
необходимо использовать среднегодовой темп прироста ВВП, НД и т.д. за рассматриваемый период.
ресурсы, которыми располагает экономика, используются с полной загрузкой, т. е. имеет место полная занятость и оптимальная загрузка производственных мощностей.
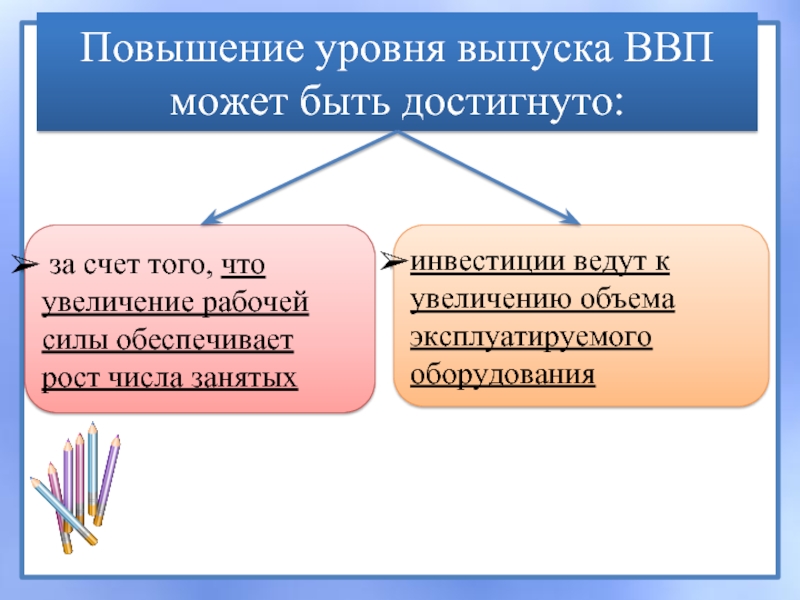
Слайд 3Повышение уровня выпуска ВВП может быть достигнуто:
за счет того, что
увеличение рабочей силы обеспечивает рост числа занятых
инвестиции ведут к увеличению объема эксплуатируемого оборудования
Слайд 4Таким образом, выпуск производимых в экономике товаров и услуг может быть
представлен как функция от двух переменных — труда (L) и капитала (К):
Q = f(L, К)
Q = f(L, К)
Слайд 5 Допустим также, что увеличение числа рабочих и объема применяемого капитала обладает
свойством постоянной отдачи, т.е. если труд и капитал увеличатся в х раз, то и выпуск продукции увеличится в х раз.
Поэтому функция:
Q = f(L, К)
может быть представлена в виде:
xQ = f(xL, хК)
Это подразумевает, что приращение числа занятых предполагает пропорциональное приращение их потребления, а приращение капитала — приращение инвестиций.
Поэтому функция:
Q = f(L, К)
может быть представлена в виде:
xQ = f(xL, хК)
Это подразумевает, что приращение числа занятых предполагает пропорциональное приращение их потребления, а приращение капитала — приращение инвестиций.
Слайд 6 Согласно системе национальных счетов, ВВП равен сумме инвестиций и личного потребления
и соответственно приращение ВВП равно сумме приращений инвестиций (I) и личного потребления (C), т. е.
ΔQ = ΔC+ ΔI
ΔQ = ΔC+ ΔI
Слайд 7Согласно теории функции потребления:
c+s = 1,
где с и s - ?.
С=сQ
С = (1-s)*Q
Таким образом:
ΔС=(1-s)*ΔQ
Слайд 8Подставляя в равенство ΔQ = ΔC+ ΔI значение ΔС, выраженное в
равенстве ΔС=(1-s)*ΔQ, имеем:
Δ Q = (1 - s)*Δ Q + Δ I
- Δ I=- Δ Q+ Δ Q-s Δ Q
- Δ I=-s Δ Q
Δ I=s Δ Q
Δ Q = (1 - s)*Δ Q + Δ I
- Δ I=- Δ Q+ Δ Q-s Δ Q
- Δ I=-s Δ Q
Δ I=s Δ Q
Слайд 9Это равенство говорит о том, что при сбалансированном росте инвестиции должны
изменяться пропорционально изменениям ВВП, причем предельная склонность к сбережениям играет роль коэффициента пропорциональности.
Если предельная склонность к сбережениям будет увеличиваться, то доля инвестиций в ВВП также должна увеличиваться, чтобы обеспечить сбалансированный рост.
Δ I=s Δ Q
Если предельная склонность к сбережениям будет увеличиваться, то доля инвестиций в ВВП также должна увеличиваться, чтобы обеспечить сбалансированный рост.
Δ I=s Δ Q
Слайд 10Теперь рассмотрим производственную функцию xQ = f(xL, хК) с точки зрения
того вклада, который делает каждый фактор в приращение ВВП.
В этом случае приращение выпуска (ΔQ) может быть представлено как сумма двух приращений выпуска:
1) за счет увеличения числа занятых (ΔQL) и
2) за счет увеличения капитала, т.е. за счет чистых инвестиций (ΔQK):
Δ Q = ΔQL+ΔQK.
В этом случае приращение выпуска (ΔQ) может быть представлено как сумма двух приращений выпуска:
1) за счет увеличения числа занятых (ΔQL) и
2) за счет увеличения капитала, т.е. за счет чистых инвестиций (ΔQK):
Δ Q = ΔQL+ΔQK.
Слайд 11Δ Q = ΔQL+ΔQK.
Теперь темп прироста ВВП может быть выражен равенством:
Δ
Q/Q = ΔQL/Q +ΔQK/Q
Обозначив темп прироста ВВП через Ʈ и полагая, что
ΔQL/Q = α*(ΔL/L) и ΔQK/Q = (1-α)*(ΔK/K)
имеем следующее выражение темпа прироста ВВП:
Ʈ = α*(ΔL/L) + (1-α)*(ΔK/K)
Параметры α и (1 - α) выражают долю труда и капитала в приросте ВВП.
Обозначив темп прироста ВВП через Ʈ и полагая, что
ΔQL/Q = α*(ΔL/L) и ΔQK/Q = (1-α)*(ΔK/K)
имеем следующее выражение темпа прироста ВВП:
Ʈ = α*(ΔL/L) + (1-α)*(ΔK/K)
Параметры α и (1 - α) выражают долю труда и капитала в приросте ВВП.
Слайд 12Разумеется, 0 ≤ а ≤1.
Предположим, что а = 0,6 и,
следовательно, (1 - а) = 0,4.
Это означает, что за счет прироста труда достигается 60% прироста ВВП, а за счет прироста капитала происходит 40% прироста ВВП.
Это означает, что за счет прироста труда достигается 60% прироста ВВП, а за счет прироста капитала происходит 40% прироста ВВП.
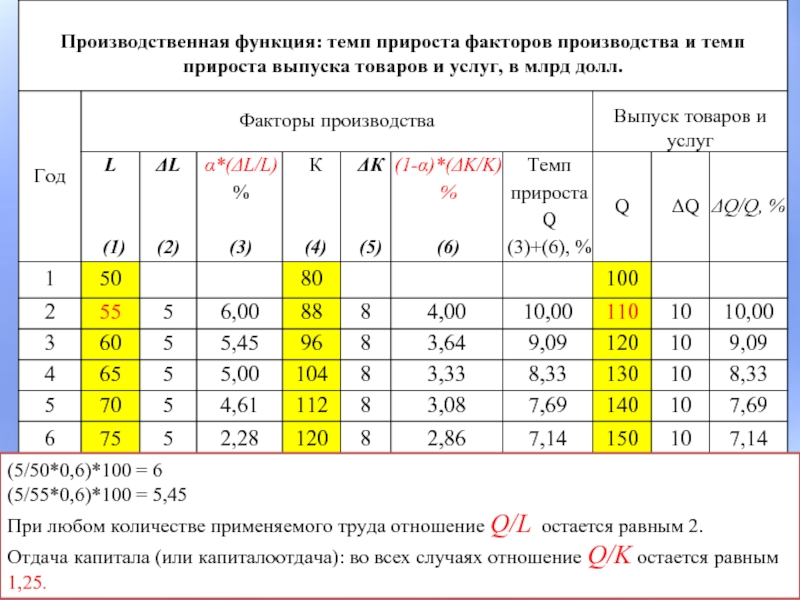
Слайд 13(5/50*0,6)*100 = 6
(5/55*0,6)*100 = 5,45
При любом количестве применяемого труда отношение Q/L
остается равным 2.
Отдача капитала (или капиталоотдача): во всех случаях отношение Q/K остается равным 1,25.
Отдача капитала (или капиталоотдача): во всех случаях отношение Q/K остается равным 1,25.
Слайд 14Экономический рост сопровождается тем, что при прежнем объеме затрат создается больший
ВВП.
Это объясняется:
- растет производительность труда
- увеличивается капиталоотдача.
Показатель, который дает обобщенную характеристику отдачи труда и капитала, называется совокупной факторной производительностью.
Это объясняется:
- растет производительность труда
- увеличивается капиталоотдача.
Показатель, который дает обобщенную характеристику отдачи труда и капитала, называется совокупной факторной производительностью.
Слайд 15Если совокупная факторная производительность растет, то выпуск продукции будет увеличиваться не
только потому, что растет количество капитала и труда, но и потому, что растет производительность труда, или капиталоотдача, или и то и другое.
Слайд 16Рост совокупной факторной производительности может быть выражен путем введения в уравнение
еще одного элемента, который играет роль третьего фактора экономического роста.
Тогда уравнение, которое устанавливает роль (долю) каждого фактора в темпе прироста ВВП, примет вид:
Ʈ = α*(ΔL/L) + (1-α)*(ΔK/K)+ (1-α)*(1/(1-с))*(ΔW/W)
где β — дополнительный фактор экономического роста, который не зависит от увеличения затрат труда и капитала.
Тогда уравнение, которое устанавливает роль (долю) каждого фактора в темпе прироста ВВП, примет вид:
Ʈ = α*(ΔL/L) + (1-α)*(ΔK/K)+ (1-α)*(1/(1-с))*(ΔW/W)
где β — дополнительный фактор экономического роста, который не зависит от увеличения затрат труда и капитала.