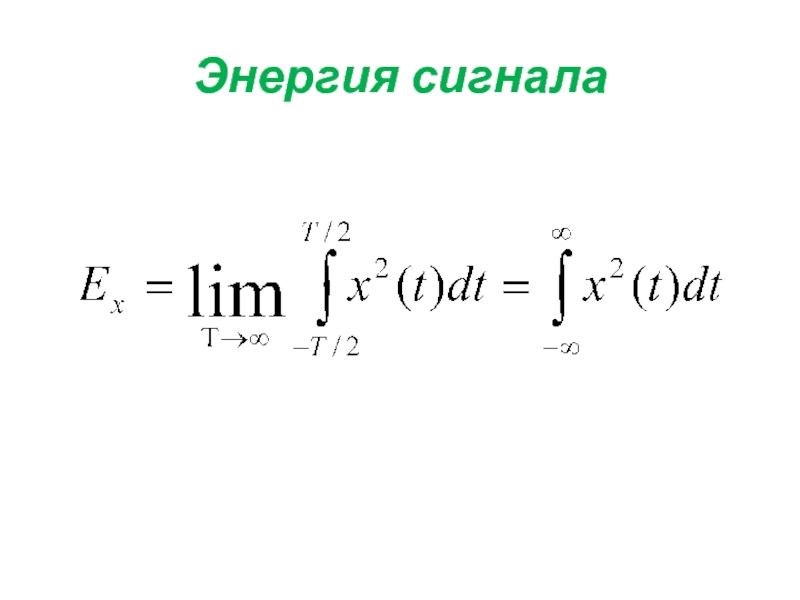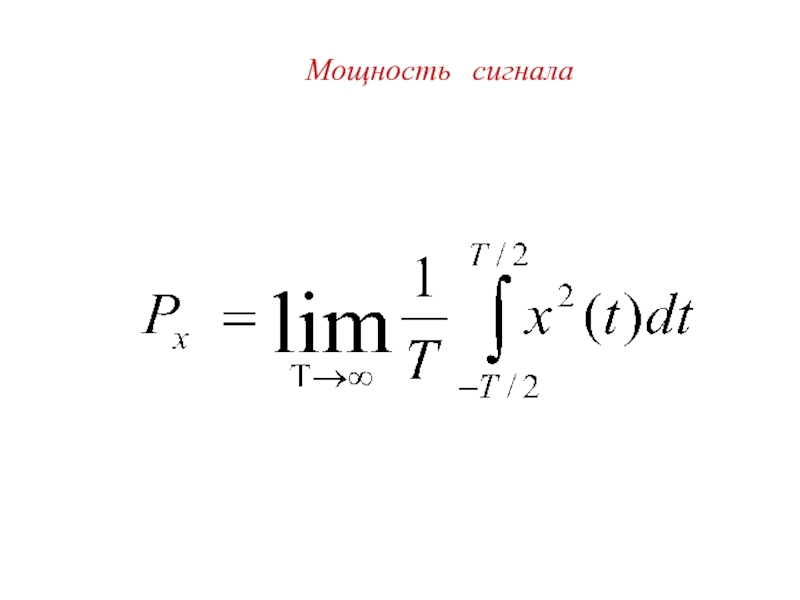- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Негізгі түсініктер мен анықтамалар. Электр сигналдарын тарату жүйесінің құрлымы презентация
Содержание
- 1. Негізгі түсініктер мен анықтамалар. Электр сигналдарын тарату жүйесінің құрлымы
- 2. Пәннің мақсаты телекоммуникациялық жүйелердегі электр сигналын таратудың
- 3. Тақырып: Негізгі түсініктер мен анықтамалар. Электр сигналдарын тарату жүйесінің құрлымы
- 4. Дәрістің мақсаты: Хабарды электр сигналына түрлендіріп тарату процестерін анықтау. Электр байланыс схемасының құрлымын анықтау.
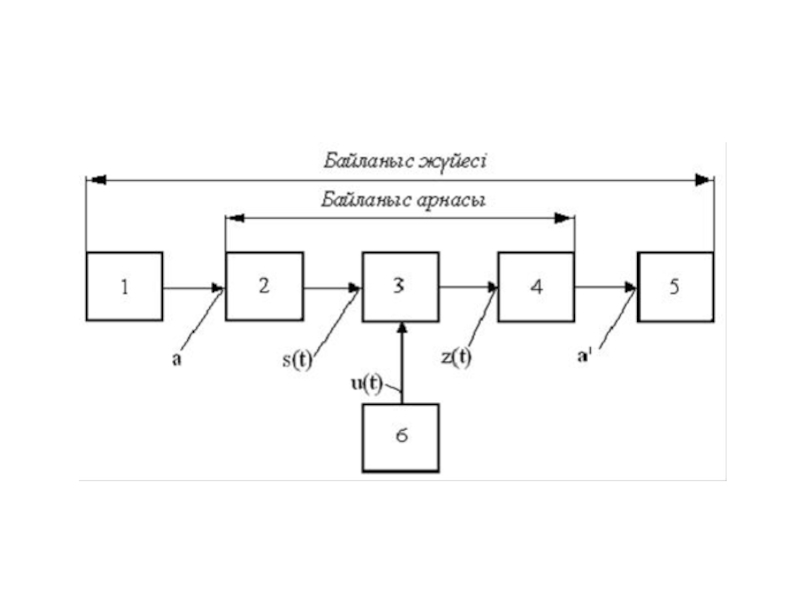
- 6. 1-хабар көзі; 2-электрлік сигналға түрлендіргіш және кодер;
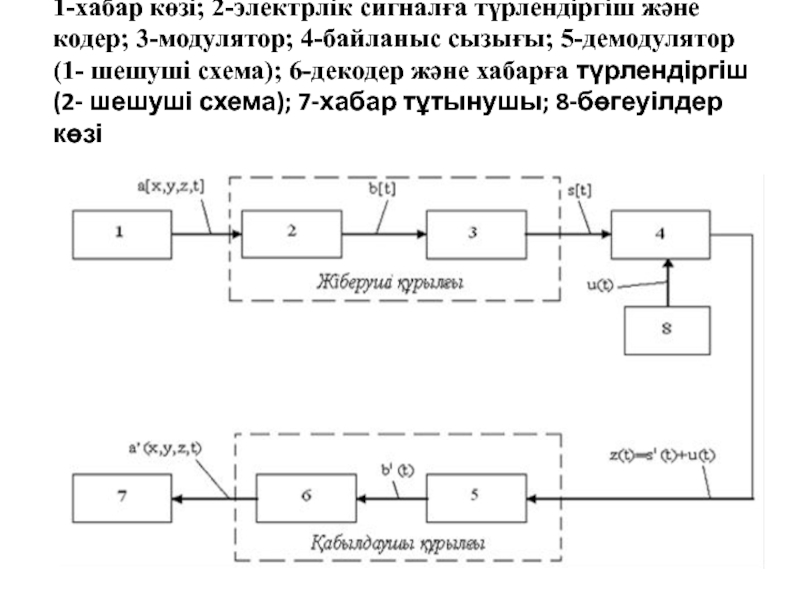
- 7. 1-хабар көзі; 2-жіберуші құрылғы; 3-байланыс
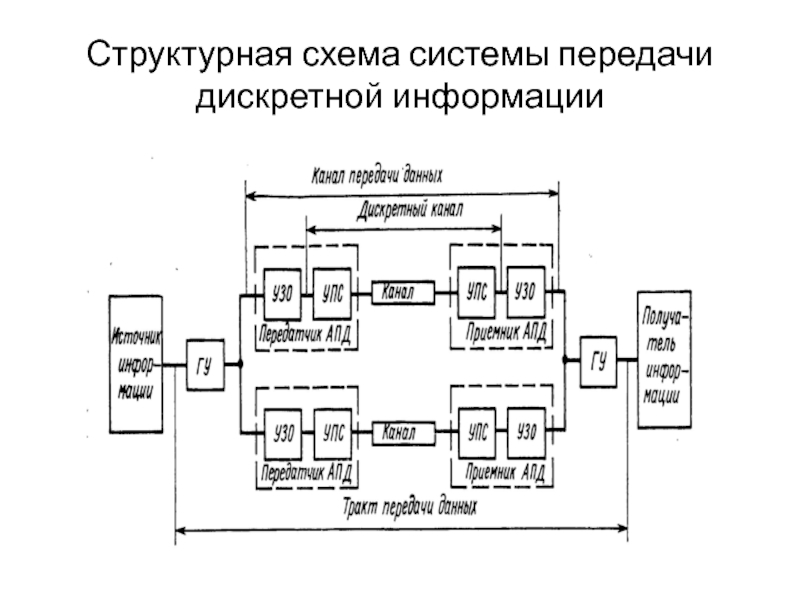
- 8. Структурная схема системы передачи дискретной информации
- 9. 1 қорек көзін
- 10. Сигнал можно классифицировать как детерминированный (при отсутствии
- 11. Периодические и непериодические сигналы Сигнал x(t) называется
- 12. Цифровой сигнал, описываемый уровнем напряжения или тока,-сигнал
- 13. Цифровые сигналы.
- 14. Аналоговый сигнал х(t) является непрерывной функцией времени,
- 16. Производительность системы связи зависит
- 17. Сигналы, выраженные через энергию или мощность
- 18. Рассеивание энергии в течении времени для реального сигнала с мгновенной мощностью
- 19. Средняя мощность
- 20. Энергия сигнала
- 21. Мощность сигнала
- 22. Энергетический сигнал
- 23. Спектральная плотность энергии
- 24. Спектральная плотность энергии x{f) является
- 25. Спектральная плотность мощности.
- 26. Автокорреляция энергетического сигнала Корреляция — это
- 27. Автокорреляция периодического сигнала
- 28. Спектральная плотность мощности и автокорреляция случайного процесса
- 30. Ортогональность сигналов
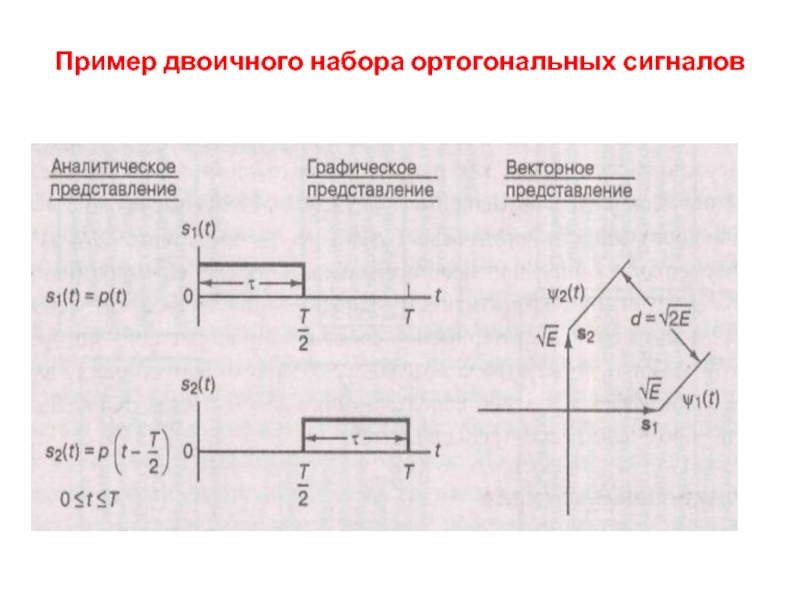
- 31. Пример двоичного набора ортогональных сигналов
Слайд 1
Әебиеттер тізімі
1.Баскаков С.И.Радиотехнические цепи и сигналы.-М: Высшая школа,2003.
Гольденберга.- М: “Радио и
2.Теория электрической связи. Под ред.Д.Д.Кловского. - М: “Радио и связь”,1999.
3.Скляр Б.Цифровая связь. - М.С-П, К.,2003.
4.Панфилов И.П.,Дырда В.Е.Теория электрической связи. - М: “Радио и связь”,1991.
5.Кловский. Д.Д., Шилкин В.А.Теория элекрической связи. – М.: Радио и связь,1990.- С.387.
6. Кунегин С.В. Системы передачи информации. Курс лекций. М.: в/ч 33965, 1997. – С. 216.
7.Ниеталин Ж.Н. Электрлік байланыс теориясы. Оқу құралы. - Алматы: РБК, 1994. – С. 164.
Слайд 2 Пәннің мақсаты телекоммуникациялық жүйелердегі электр сигналын таратудың негізгі заңдылықтарын оқып білу.
Слайд 4Дәрістің мақсаты: Хабарды электр сигналына түрлендіріп тарату процестерін анықтау. Электр байланыс
Слайд 61-хабар көзі; 2-электрлік сигналға түрлендіргіш және кодер; 3-модулятор; 4-байланыс сызығы; 5-демодулятор
Слайд 71-хабар көзі;
2-жіберуші құрылғы;
3-байланыс сызығы;
4-қабылдаушы құрылғы;
5-хабар тұтынушы;
6-бөгеуілдер көзі
Слайд 9 1 қорек көзін форматтау и кодтау 2 видиосигдарды тарату 3 Жолақты сигналдарды
Слайд 10Сигнал можно классифицировать как детерминированный (при отсутствии неопределенности относительно его значения
Слайд 11Периодические и непериодические сигналы Сигнал x(t) называется периодическим во времени, если существует
Слайд 12Цифровой сигнал, описываемый уровнем напряжения или тока,-сигнал (импульс - для узкополосной
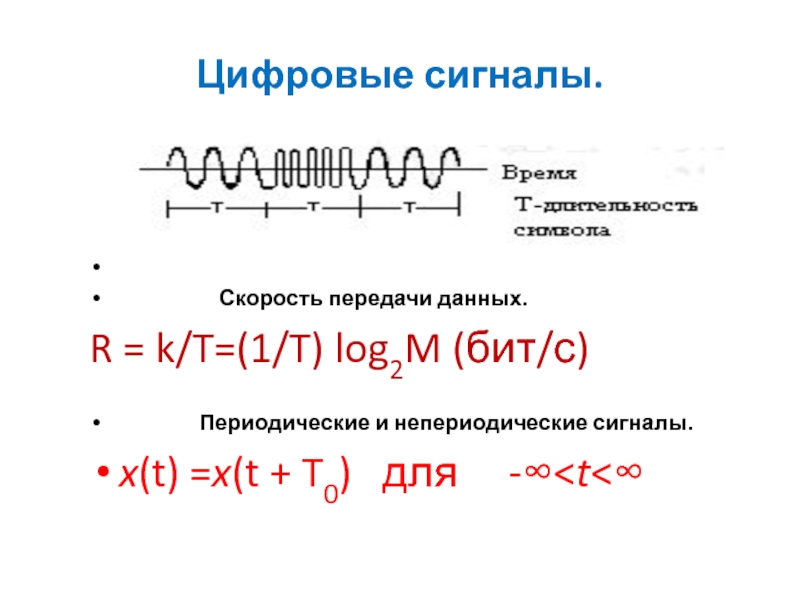
Слайд 13Цифровые сигналы.
R = k/T=(1/T) log2M (бит/с)
Периодические и непериодические сигналы.
x(t) =x(t + T0) для -∞
Слайд 14Аналоговый сигнал х(t) является непрерывной функцией времени, т.е. х(t) однозначно определяется
Слайд 15
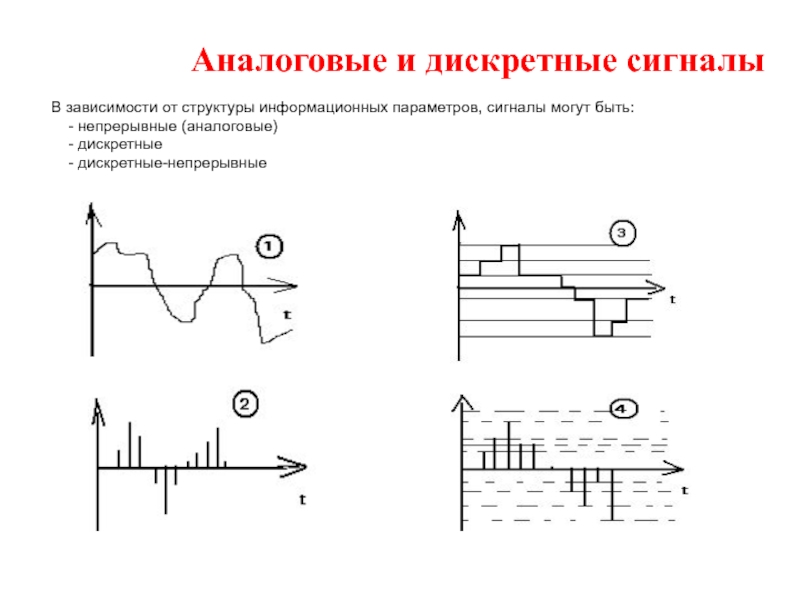
В зависимости от структуры информационных параметров, сигналы могут быть:
- непрерывные (аналоговые)
- дискретные
- дискретные-непрерывные
.
Слайд 16 Производительность системы связи зависит от энергии принятого сигнала; сигналы с более
Слайд 17Сигналы, выраженные через энергию или мощность
p{t)=ν2(t)/R
p{t)=i2(t)R
p{t)=x2(t) где x(t) — это
Р(t)-мгновенная мощность
Слайд 24Спектральная плотность энергии
x{f) является спектральной плотностью энергии (ESD) сигнала x(t).
Величина
Слайд 25Спектральная плотность мощности.
Gx(f) Спектральная плотность мощности (PSD) периодического
Слайд 26Автокорреляция энергетического сигнала Корреляция — это процесс согласования; автокорреляцией называется
4.
значение в нуле равно энергии сигнала
3.
автокорреляция и ESD являются Фурье - образами друг друга, что обозначается двусторонней стрелкой
2.
для всех
максимальное значение в нуле
.
симметрия по t относительно нуля
1.
Автокорреляционная функция действительного энергетического сигнала имеет следующие свойства:
Слайд 27Автокорреляция периодического сигнала
значение в нуле равно энергии сигнала
автокорреляция и ESD являются
для всех
максимальное значение в нуле
симметрия по t относительно нуля
1.
2.
3.
4.
Автокорреляция периодического сигнала, принимающего действительные значения, имеет свойства, сходные со свойствами энергетического сигнала.
Слайд 28Спектральная плотность мощности и автокорреляция случайного процесса Основные свойства функций спектральной плотности
4. Рх =
2. Gx(f) = Gx (-f)
1. Gx(f) > 0
связь между средней нормированной мощностью и спектральной плотностью мощности
автокорреляция и спектральная плотность мощности являются Фурье - образами друг друга
для X(t), принимающих действительные значения
всегда принимает действительные значения
3.