- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Экономико-математический практикум презентация
Содержание
- 1. Экономико-математический практикум
- 2. Список литературы А.И. Стрикалов, И.А. Печенежская. Экономико-математические
- 3. Модель – образ реального объекта в материальной
- 4. Этапы экономико-математического моделирования Постановка экономической цели и
- 5. Математические методы решения некоторых задач менеджмента
- 6. Основные понятия теории графов Теория графов –
- 7. Оптимизация на графах. Принятие решений методом построения
- 8. Построение дерева решений и анализ альтернатив 1
- 9. Используя дерево решений помогите предпринимателю принять решение.
- 10. Использование математических графов в сетевом планировании To= 0.4 Tmax+ 0.6Tmin Kсл= Nраб/Nсоб 1< Kсл
- 11. Математические расчеты при проведении балансировки линий сборки
- 12. Создание модели линий сборки 1 2 3
- 13. 2. Определим теоретически минимальное число рабочих мест:
- 14. Решить задачу балансировки линии сборки Заключительная сборка
- 15. Задача определения кратчайшего пути 7 6 4
- 16. Задача определения кратчайшего пути 7 6 4
- 17. Решите задачу 1 4 2 7 5
- 18. Построение коммуникационной сети минимальной длины Университет устанавливает
- 19. Построение коммуникационной сети минимальной длины Алгоритм построения:
- 20. Фирма получила заказ на прокладку кабеля для
- 21. Решение задач менеджмента с помощью эконометрических моделей
- 22. Виды регрессионных моделей Y X
- 23. Линейная парная регрессия У Х
- 24. Коэффициент корреляции Выборочный коэффициент корреляции r является
- 25. Коэффициент детерминации Коэффициент детерминации – мера качества
- 26. Свойства коэффициента детерминации Чем ближе коэффициент детерминации
- 27. Основы множественного регрессионного анализа Цель: исследовать зависимость
- 28. Эконометрическая модель множественной линейной регрессии в матричной
- 29. Построение эконометрической модели множественной линейной регрессии ŷi=b0+b1xi1+b2xi2
- 30. Стандартизированные коэффициенты регрессии и коэффициенты эластичности На
- 31. Множественный и скорректированный коэффициент детерминации - множественный
- 32. Математическая модель управления запасами q t A
- 33. Математическая модель управления запасами с учетом скидки
- 34. Модель планирования дефицита (случай невыполнения заявок) Уровень
- 35. Модель планирования дефицита (случай выполнения заявок) Уровень
- 36. Решение общей задачи линейного программирования (задача оптимального
- 37. Решение общей задачи линейного программирования (задача о
- 38. Составьте модель для следующих задач Пусть диетолог
- 39. Задача о раскрое Строительная фирма заказала изготовить
- 40. Транспортная задача На двух складах А1 и
- 41. Графический метод решения задачи линейного программирования Х1
- 42. Спасибо за внимание !
Слайд 1Экономико-математический практикум
Автор: Захарова Лариса Александровна, к.ф.м.н., доцент кафедры ТПУО
Слайд 2Список литературы
А.И. Стрикалов, И.А. Печенежская. Экономико-математические методы и модели. Ростов –
Г.И. Просветов. Математические методы и модели в экономике (задачи и решения). Москва: Альфа Пресс, 2008.
О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных. Математические методы в экономике. Москва: Дело и Сервис, 2009.
В.И. Ширяев, И.А. Баев, Е.В. Ширяев. Управление предприятием: моделирование, анализ, управление. Москва: Книжный дом «ЛИБРОКОМ», 2009.
В.В. Покровский. Математические методы в бизнесе и менеджменте. Москва: БИНОМ. Лаборатория знаний, 2008
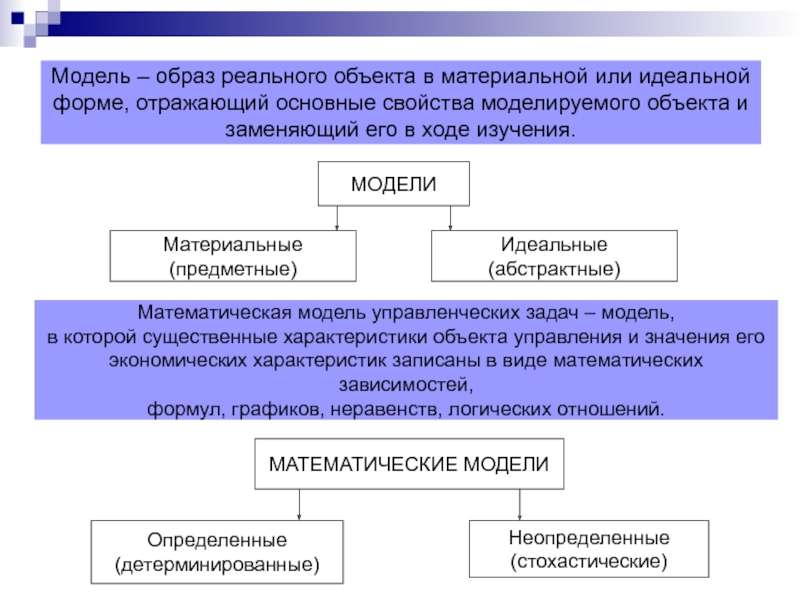
Слайд 3Модель – образ реального объекта в материальной или идеальной форме, отражающий
МОДЕЛИ
Материальные
(предметные)
Идеальные
(абстрактные)
Математическая модель управленческих задач – модель,
в которой существенные характеристики объекта управления и значения его
экономических характеристик записаны в виде математических зависимостей,
формул, графиков, неравенств, логических отношений.
МАТЕМАТИЧЕСКИЕ МОДЕЛИ
Определенные
(детерминированные)
Неопределенные
(стохастические)
Слайд 4Этапы экономико-математического моделирования
Постановка экономической цели и формирование критериев;
Подготовка исходной информации;
Построение математической
Математический анализ модели;
Численные вычисления;
Анализ численных результатов и их применение.
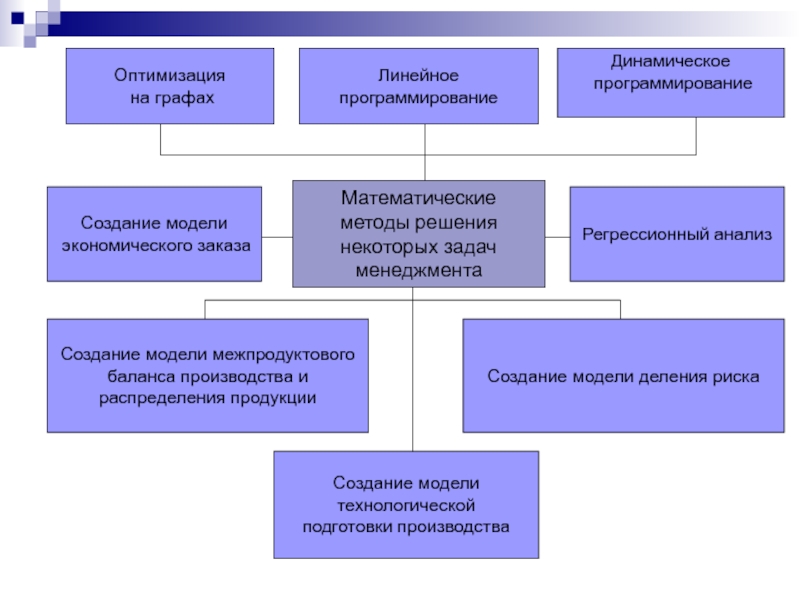
Слайд 5Математические
методы решения
некоторых задач
менеджмента
Оптимизация
на графах
Линейное
программирование
Динамическое
программирование
Создание модели
экономического заказа
Создание
баланса производства и
распределения продукции
Создание модели
технологической
подготовки производства
Регрессионный анализ
Создание модели деления риска
Слайд 6Основные понятия теории графов
Теория графов – это раздел математики, включающий в
Графом G(X,U) называется совокупность двух множеств: непустого множества Х (вершин) и множества U (ребер)
Х1
Х2
Х1
Х2
U1
U1
неограф
орграф
Слайд 7Оптимизация на графах. Принятие решений методом построения деревьев решений
Дерево решений –
управленческого решения, в котором отражены альтернативные решения,
альтернативные состояния среды, соответствующие вероятности и
выигрыши для любых комбинаций альтернатив и состояний среды
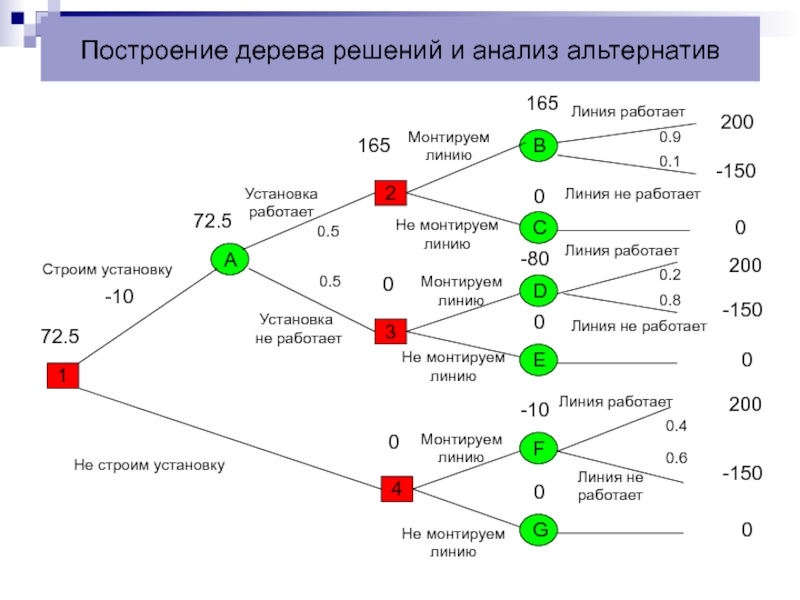
Главному инженеру компании надо решить монтировать или нет новую
производственную линию. Если новая линия будет работать безотказно,
компания получит прибыль 200 млн. руб. Если она откажет, компания
получит убыток 150 млн. руб. По оценкам главного инженера, существует
60% шансов, что линия откажет. Можно создать экспериментальную
Установку, а затем уже монтировать или нет производственную линию.
Эксперимент обойдется в 10 млн. руб. Существует 50% шансов, что
Установка будет работать. Если установка будет работать, то 90% шансов
За то, что будет работать и линия. Если установка работать не будет, то
только 20% шансов за то, что линия заработает. Какое решение нужно
принять главному инженеру?
Слайд 8Построение дерева решений и анализ альтернатив
1
2
3
4
А
B
C
D
E
F
G
Строим установку
Не строим установку
Установка
работает
Установка
не работает
Монтируем
линию
Не
линию
Монтируем
линию
Монтируем
линию
Не монтируем
линию
Не монтируем
линию
Линия работает
Линия работает
Линия работает
Линия не работает
Линия не работает
Линия не работает
200
200
200
-150
-150
-150
0
0
0
0.9
0.1
0.2
0.8
0.4
0.6
165
165
0
-80
0
0
-10
0
0
72.5
72.5
0.5
0.5
-10
Слайд 9Используя дерево решений помогите предпринимателю принять решение. Какова ожидаемая стоимостная оценка
Предприниматель провел анализ, связанный с открытием магазина. Если он откроет большой магазин, то при благоприятном состоянии рынка получит прибыль 60 млн. рублей, при неблагоприятном – понесет убытки 40 млн. рублей. Маленький магазин принесет ему 30 млн. рублей прибыли при благоприятном состоянии рынка и 10 млн. рублей убытков при неблагоприятном. Возможность благоприятного и неблагоприятного состояния рынка он оценивает одинаково. Исследование рынка, которое может провести специалист, обойдется предпринимателю в 5 млн. рублей. Специалист считает, что с вероятностью 0,6 состояние рынка окажется благоприятным. В то же время при положительном заключении состояние рынка окажется благоприятным лишь с вероятностью 0,9. при отрицательном заключении с вероятностью 0,12 состояние рынка может оказаться благоприятным.
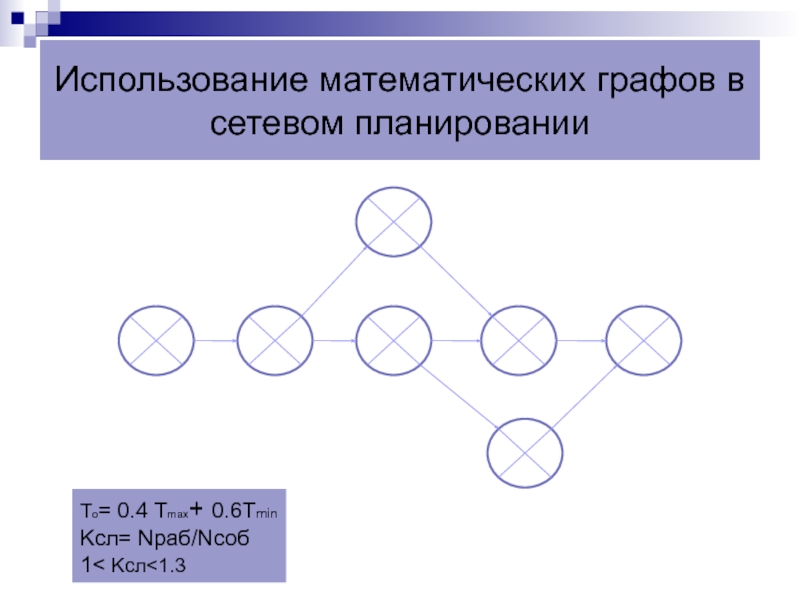
Слайд 10Использование математических графов в сетевом планировании
To= 0.4 Tmax+ 0.6Tmin
Kсл= Nраб/Nсоб
1< Kсл
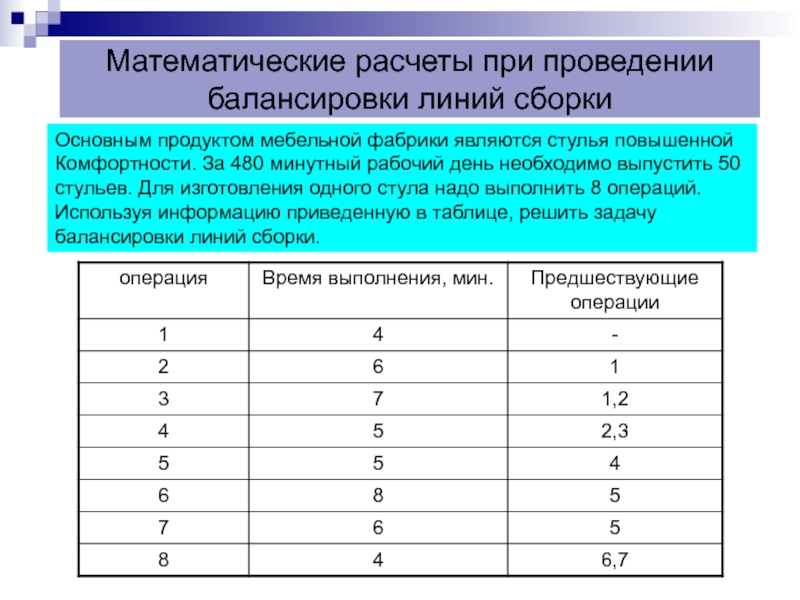
Слайд 11Математические расчеты при проведении балансировки линий сборки
Основным продуктом мебельной фабрики являются
Комфортности. За 480 минутный рабочий день необходимо выпустить 50
стульев. Для изготовления одного стула надо выполнить 8 операций.
Используя информацию приведенную в таблице, решить задачу
балансировки линий сборки.
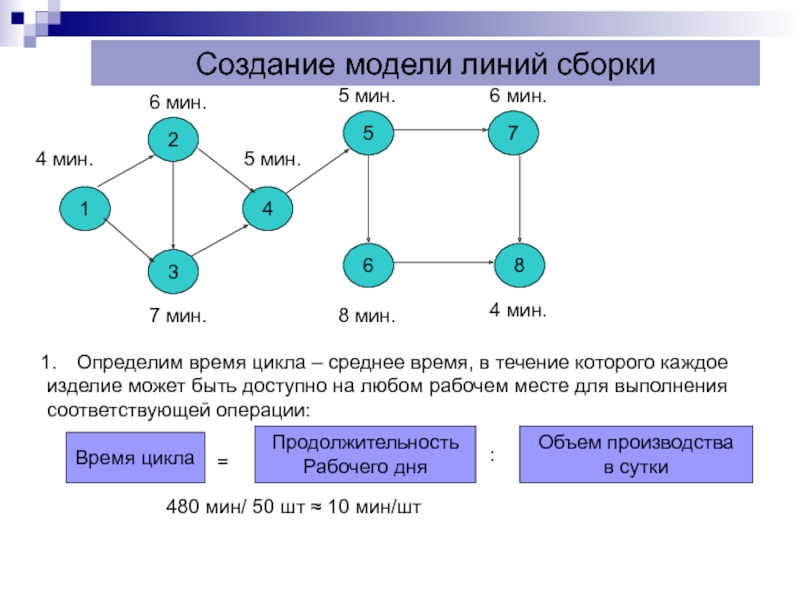
Слайд 12Создание модели линий сборки
1
2
3
4
5
6
7
8
4 мин.
6 мин.
7 мин.
5 мин.
5 мин.
8 мин.
6 мин.
4
Определим время цикла – среднее время, в течение которого каждое
изделие может быть доступно на любом рабочем месте для выполнения
соответствующей операции:
Время цикла
=
Продолжительность
Рабочего дня
:
Объем производства
в сутки
480 мин/ 50 шт ≈ 10 мин/шт
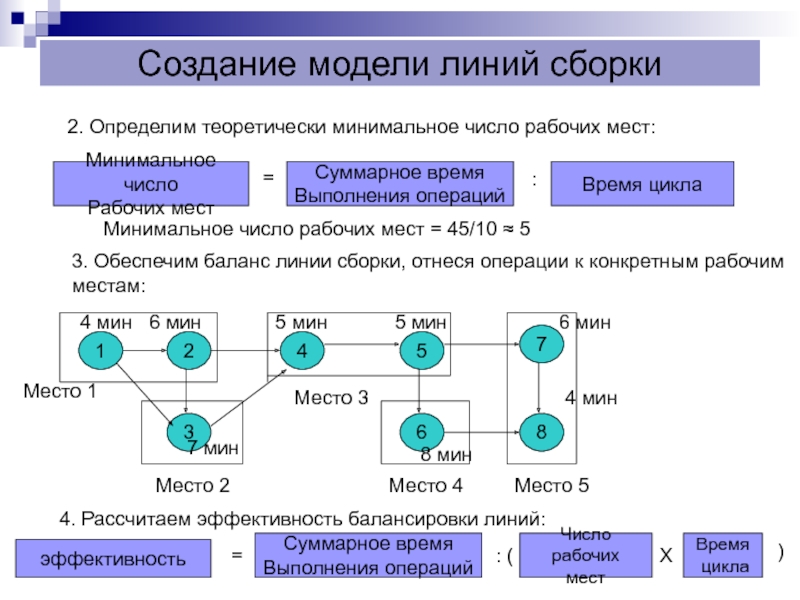
Слайд 132. Определим теоретически минимальное число рабочих мест:
Создание модели линий сборки
Минимальное число
Рабочих
Суммарное время
Выполнения операций
Время цикла
=
:
Минимальное число рабочих мест = 45/10 ≈ 5
3. Обеспечим баланс линии сборки, отнеся операции к конкретным рабочим
местам:
1
2
3
4
5
6
7
8
4 мин
6 мин
7 мин
5 мин
5 мин
8 мин
6 мин
4 мин
Место 1
Место 2
Место 3
Место 4
Место 5
4. Рассчитаем эффективность балансировки линий:
эффективность
=
Число рабочих
мест
Суммарное время
Выполнения операций
: (
Х
Время
цикла
)
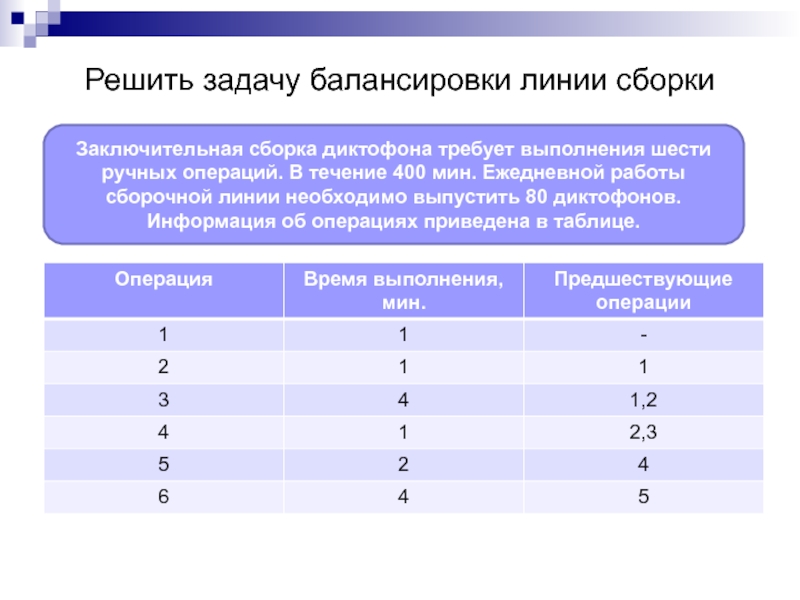
Слайд 14Решить задачу балансировки линии сборки
Заключительная сборка диктофона требует выполнения шести ручных
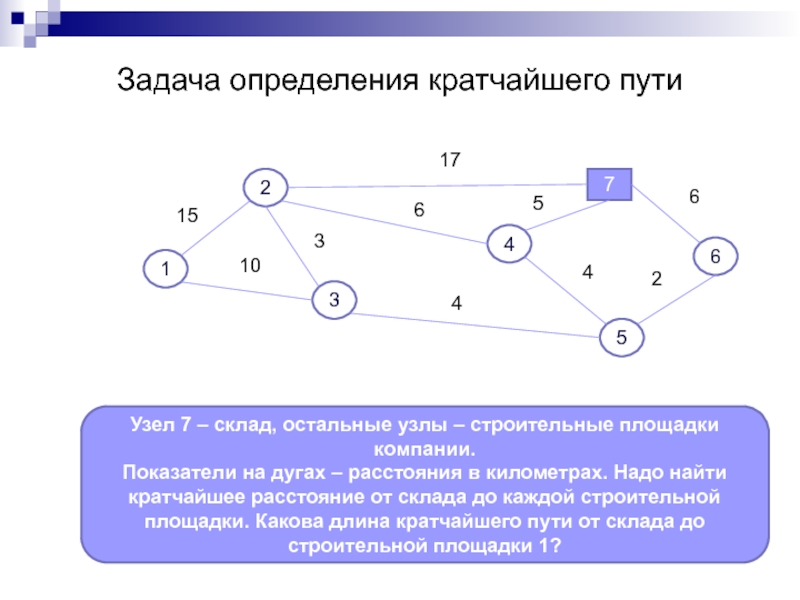
Слайд 15Задача определения кратчайшего пути
7
6
4
3
1
2
5
15
17
6
5
10
3
4
4
6
2
Узел 7 – склад, остальные узлы – строительные
Показатели на дугах – расстояния в километрах. Надо найти кратчайшее расстояние от склада до каждой строительной площадки. Какова длина кратчайшего пути от склада до строительной площадки 1?
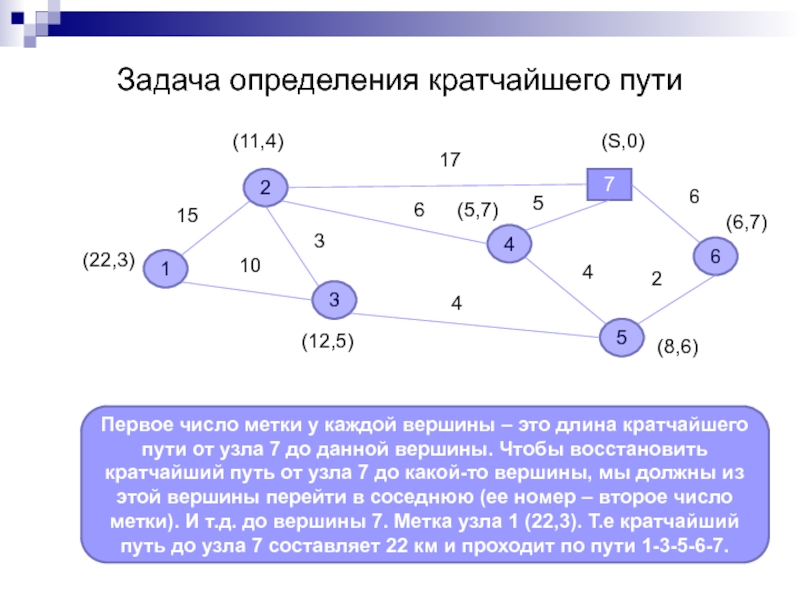
Слайд 16Задача определения кратчайшего пути
7
6
4
3
1
2
5
15
17
6
5
10
3
4
4
6
2
Первое число метки у каждой вершины – это
(11,4)
(22,3)
(12,5)
(5,7)
(6,7)
(8,6)
(S,0)
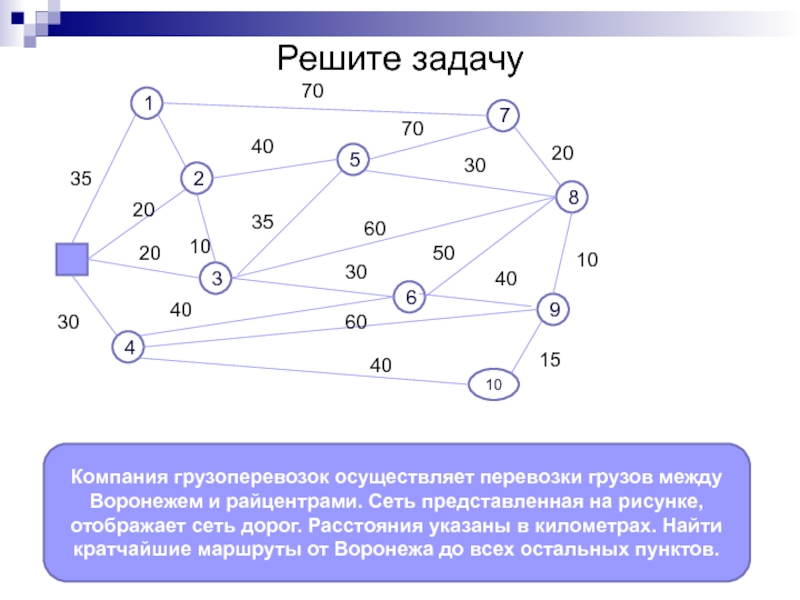
Слайд 17Решите задачу
1
4
2
7
5
8
6
9
10
3
35
20
10
20
30
70
70
40
35
20
30
10
60
30
50
40
15
40
60
40
Компания грузоперевозок осуществляет перевозки грузов между Воронежем и райцентрами. Сеть
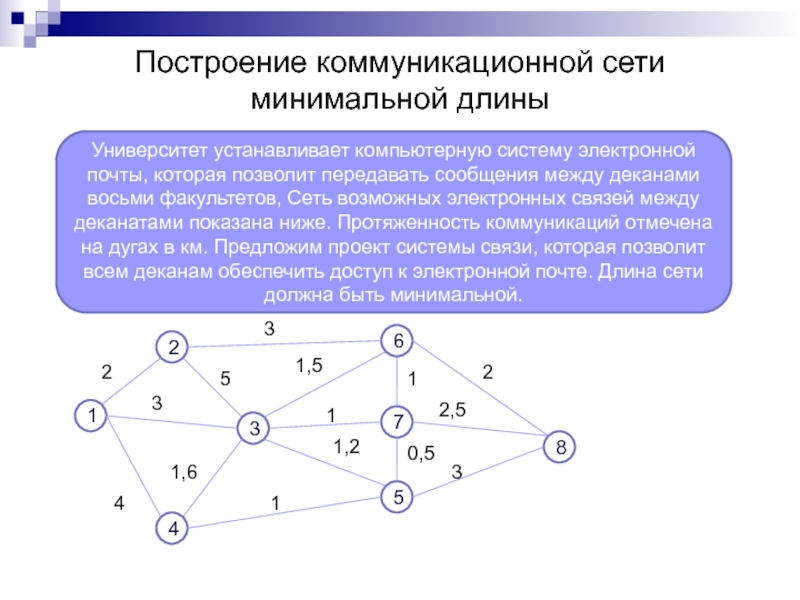
Слайд 18Построение коммуникационной сети минимальной длины
Университет устанавливает компьютерную систему электронной почты, которая
1
7
8
5
4
3
6
2
2
4
3
5
3
1,6
1
3
2
1
1
1,5
2,5
1,2
0,5
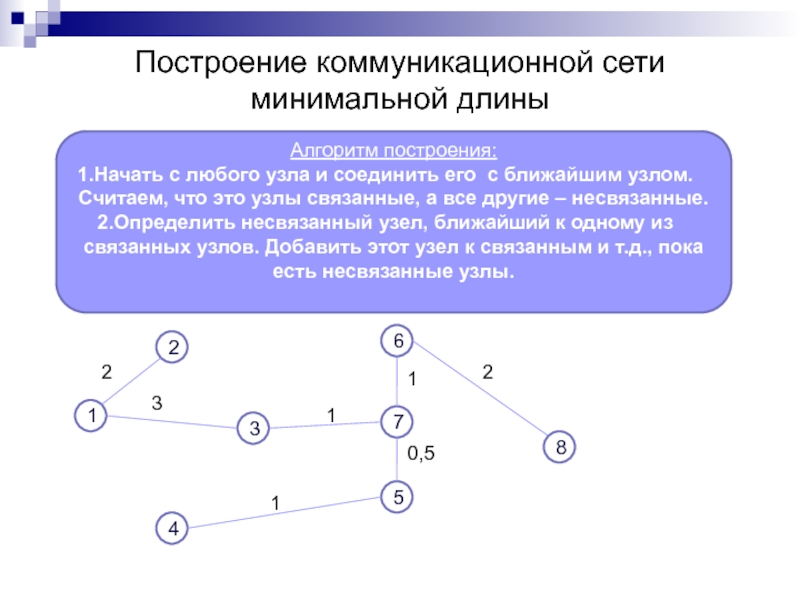
Слайд 19Построение коммуникационной сети минимальной длины
Алгоритм построения:
Начать с любого узла и соединить
Определить несвязанный узел, ближайший к одному из связанных узлов. Добавить этот узел к связанным и т.д., пока есть несвязанные узлы.
1
7
8
5
4
3
6
2
2
3
1
2
1
1
0,5
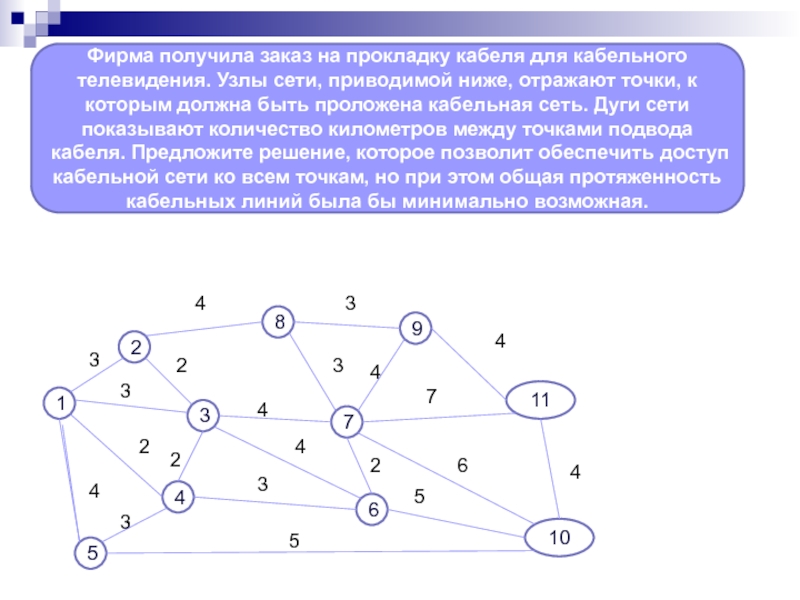
Слайд 20Фирма получила заказ на прокладку кабеля для кабельного телевидения. Узлы сети,
1
11
9
8
2
3
7
4
5
6
10
3
4
3
4
4
7
6
5
5
3
4
2
4
3
4
2
3
2
4
3
2
Слайд 21Решение задач менеджмента с помощью эконометрических моделей
Эконометрика – раздел математической экономики,
осуществить статистическую оценку и анализ экономических зависимостей
и моделей на основе изучения эмпирических данных.
Y = F(X) +ε – эконометрическая модель
Y- наблюдаемое значение объясняемой переменной
F(X) – объясненная часть, зависящая от значений объясняемых переменных
ε - случайная составляющая
Выбор вида регрессионной модели (линейная или нелинейная, парная или множественная );
Расчет коэффициентов регрессии;
Расчет коэффициента корреляции и коэффициента детерминации
Определение значимости коэффициентов регрессии и уравнения регрессии
Нахождение доверительных интервалов для уравнения регрессии
Алгоритм построения модели
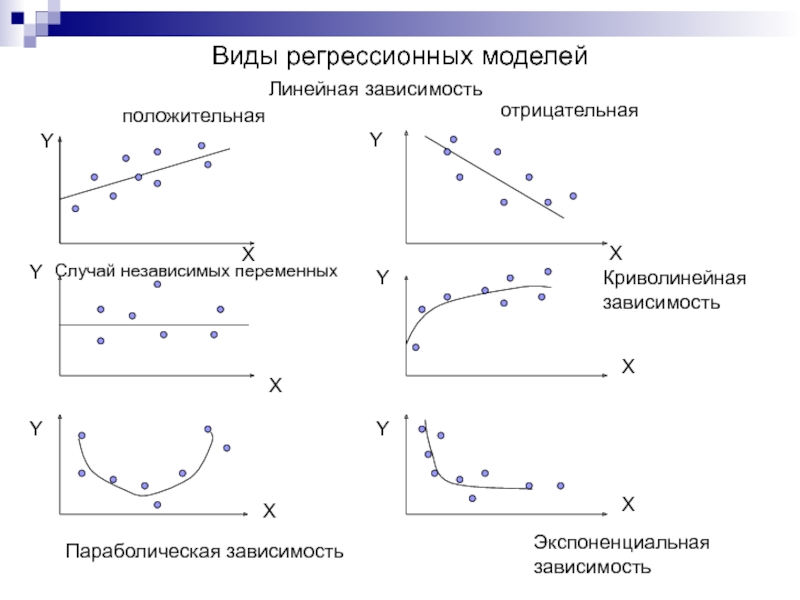
Слайд 22Виды регрессионных моделей
Y
X
Y
X
Y
X
Y
Y
Y
X
X
X
Линейная зависимость
положительная
отрицательная
Случай независимых переменных
Криволинейная
зависимость
Экспоненциальная
зависимость
Параболическая зависимость
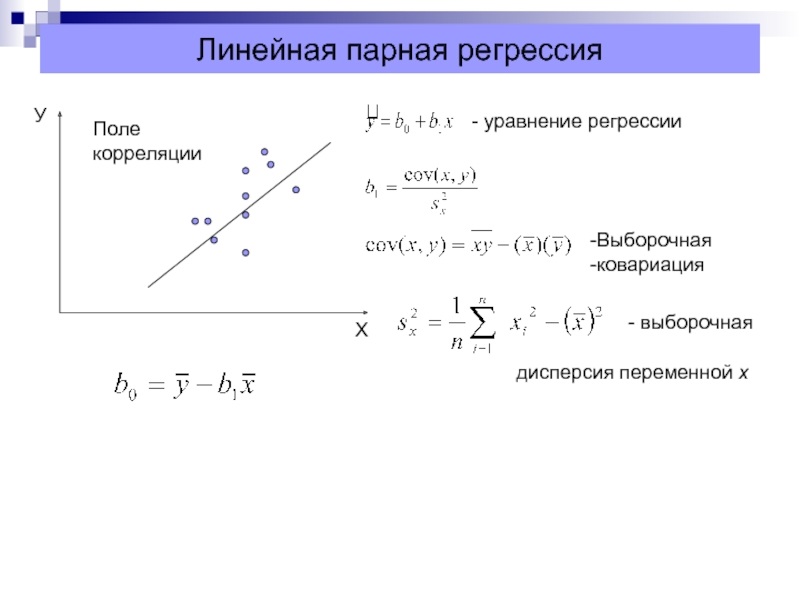
Слайд 23Линейная парная регрессия
У
Х
Поле
корреляции
- уравнение регрессии
Выборочная
ковариация
- выборочная
дисперсия переменной х
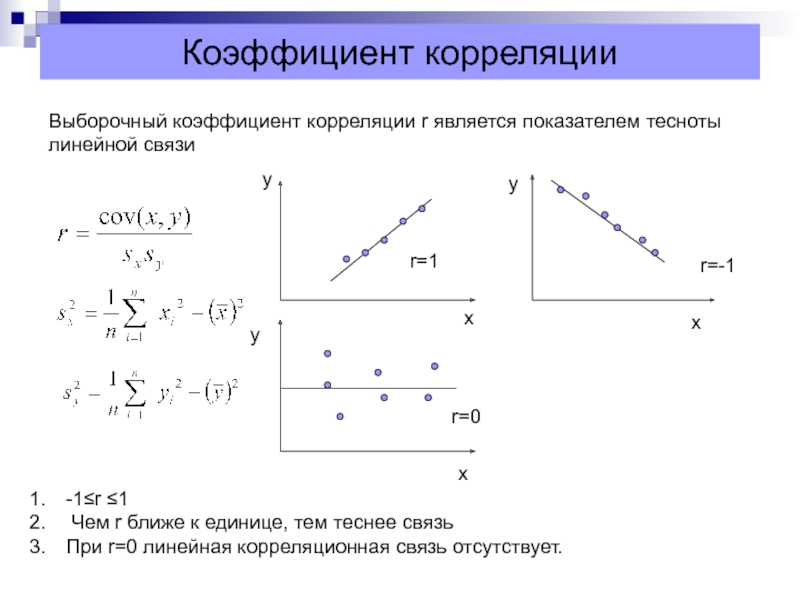
Слайд 24Коэффициент корреляции
Выборочный коэффициент корреляции r является показателем тесноты
линейной связи
у
у
у
х
х
х
r=1
r=-1
r=0
-1≤r ≤1
Чем
При r=0 линейная корреляционная связь отсутствует.
Слайд 25Коэффициент детерминации
Коэффициент детерминации – мера качества уравнения регрессии,
характеристика прогностической силы анализируемой
общая сумма квадратов отклонений зависимой
переменной от средней
остаточная сумма квадратов, характеризующая
влияние неучтенных факторов
- сумма квадратов, обусловленная регрессией
Показывает, какая доля вариации зависимой
переменной обусловлена вариацией объясняющей
переменной.
Слайд 26Свойства коэффициента детерминации
Чем ближе коэффициент детерминации к единице, тем лучше регрессия
Если коэффициент детерминации равен единице, то эмпирические точки лежат на линии регрессии и меду переменными х и у существует линейная функциональная связь;
Если коэффициент детерминации равен нулю, то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, а линия регрессии параллельна оси абсцисс.
Слайд 27Основы множественного регрессионного анализа
Цель: исследовать зависимость одной переменной Y от нескольких
объясняющих
Модель множественной линейной регрессии можно представить в виде:
Где β – коэффициенты регрессии, р – число объясняющих переменных,
включаемых в модель, i- число наблюдений, х – значения объясняющих
переменных для у
Слайд 28Эконометрическая модель множественной линейной регрессии в матричной форме
Включение в регрессионную модель
приводит к целесообразности использования матричных обозначений.
Матричное описание регрессии облегчает как теоретические концепции
анализа, так и необходимые расчетные процедуры.
Y=Xβ+ε
- модель в матричной форме
- матрица значений объясняющих переменных
β= (β0 β1……βp)
ε= (ε1 ε2……. εn)
-вектор- столбец коэффициентов регрессии
- вектор-столбец возмущений, случайных ошибок
Слайд 29Построение эконометрической модели множественной линейной регрессии
ŷi=b0+b1xi1+b2xi2
Эконометрическая модель для двух объясняющих
переменных
Для определения коэффициентов регрессии воспользуемся формулой
Где Х – матрица объясняющих
переменных,
У – вектор столбец значений
объясняемых переменных
Слайд 30Стандартизированные коэффициенты регрессии и коэффициенты эластичности
На практике часто бывает необходимо сравнения
переменную различных объясняемых переменных, когда последние
выражаются разными единицами измерения. В этом случае вводят
стандартизированные коэффициенты регрессии и коэффициенты эластичности
Показывает на сколько величин Sy изменится
в среднем переменная У при увеличении только
1 объясняющей переменной на Sx1
Показывает на сколько % изменится
в среднем переменная У при увеличении только
1 объясняющей переменной на 1%
Слайд 31Множественный и скорректированный коэффициент детерминации
- множественный коэффициент детерминации
Имеет недостаток, в том,
новых объясняющих переменных, хотя при этом качество модели
может не улучшаться, поэтому вводят скорректированный
коэффициент детерминации
Значимость уравнения регрессии определяем
с помощью F – критерия Фишера- Снедекора
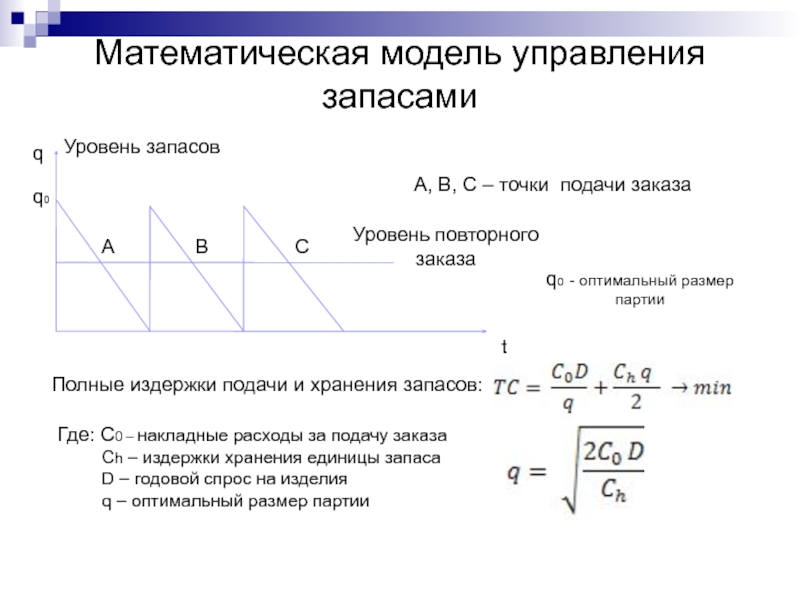
Слайд 32Математическая модель управления запасами
q
t
A
B
C
Уровень запасов
Уровень повторного
заказа
А, В, С – точки подачи
q0 - оптимальный размер
партии
q0
Полные издержки подачи и хранения запасов:
Где: С0 – накладные расходы за подачу заказа
Сh – издержки хранения единицы запаса
D – годовой спрос на изделия
q – оптимальный размер партии
Слайд 33Математическая модель управления запасами с учетом скидки на количество
Постоянные издержки обслуживания
Где: С – закупочная цена
Годовой спрос на изделие составляет 1000 единиц, стоимость подачи заказа 40 рублей за заказ, закупочная цена составляет 50 рублей за единицу, годовая стоимость хранения одной единицы продукции составляет25% от закупочной цены. Можно получить скидку 3% у поставщиков, если размер партии будет составлять не менее 200 изделий. Стоит ли воспользоваться скидкой?
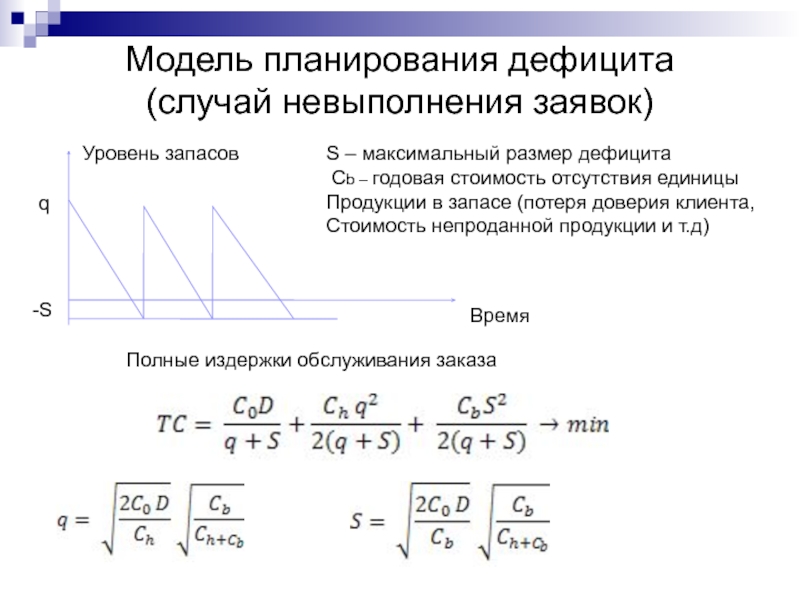
Слайд 34Модель планирования дефицита
(случай невыполнения заявок)
Уровень запасов
Время
q
-S
S – максимальный размер дефицита
Cb
Продукции в запасе (потеря доверия клиента,
Стоимость непроданной продукции и т.д)
Полные издержки обслуживания заказа
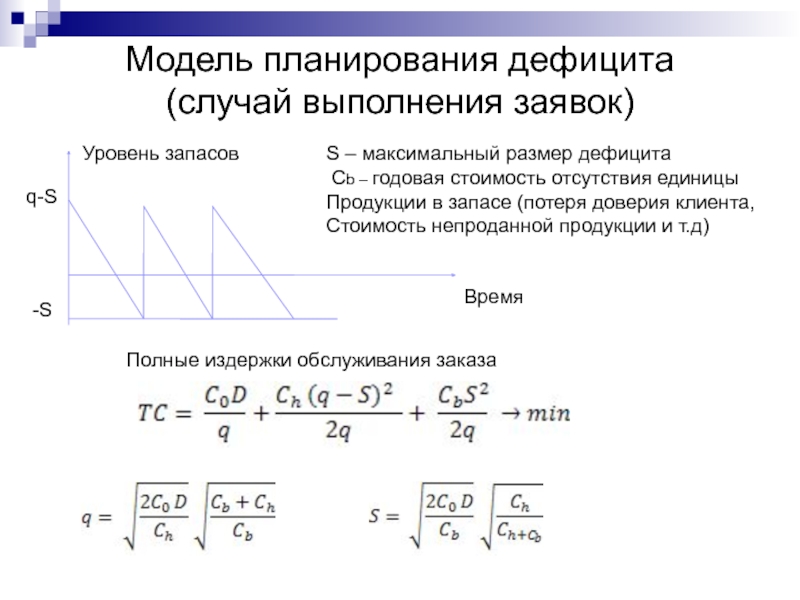
Слайд 35Модель планирования дефицита
(случай выполнения заявок)
Уровень запасов
Время
q-S
-S
S – максимальный размер дефицита
Cb
Продукции в запасе (потеря доверия клиента,
Стоимость непроданной продукции и т.д)
Полные издержки обслуживания заказа
Слайд 36Решение общей задачи линейного программирования
(задача оптимального расходования ресурсов)
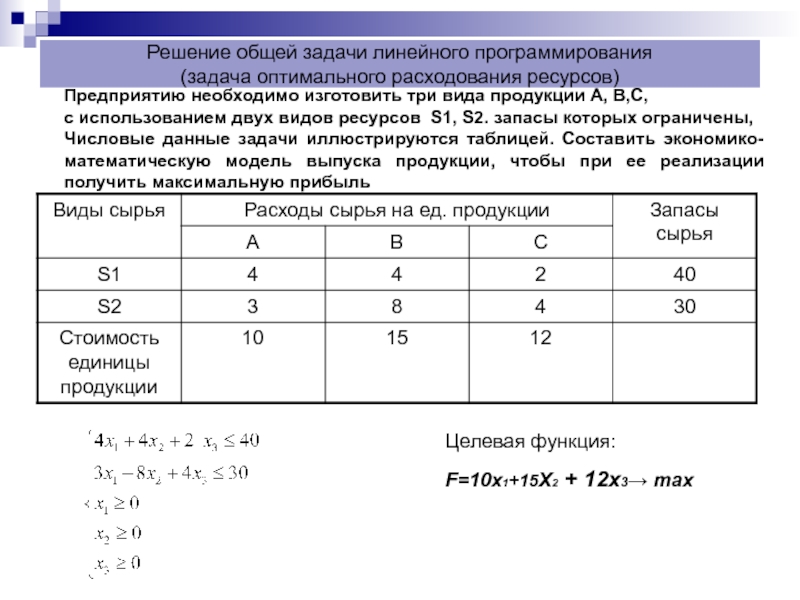
Предприятию необходимо изготовить три
с использованием двух видов ресурсов S1, S2. запасы которых ограничены,
Числовые данные задачи иллюстрируются таблицей. Составить экономико-математическую модель выпуска продукции, чтобы при ее реализации получить максимальную прибыль
Целевая функция:
F=10x1+15X2 + 12х3→ max
Слайд 37Решение общей задачи линейного программирования
(задача о смесях)
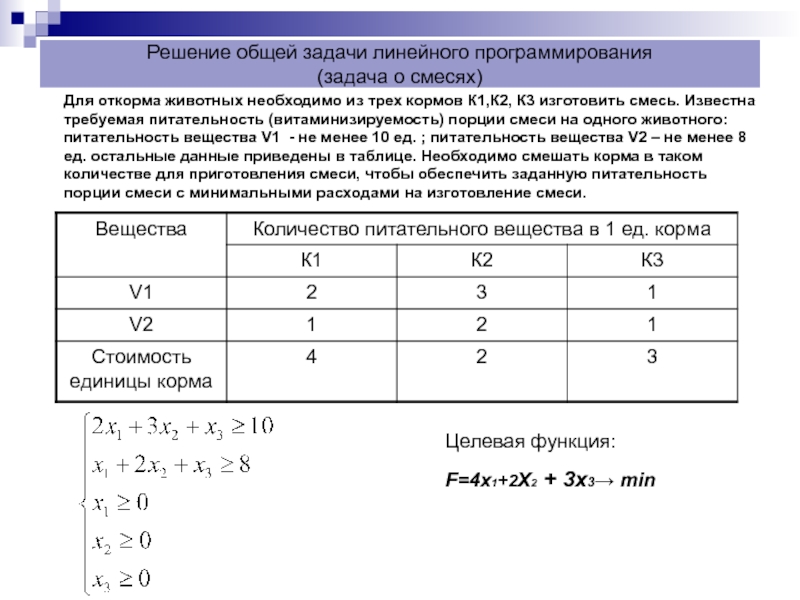
Для откорма животных необходимо из
Целевая функция:
F=4x1+2X2 + 3х3→ min
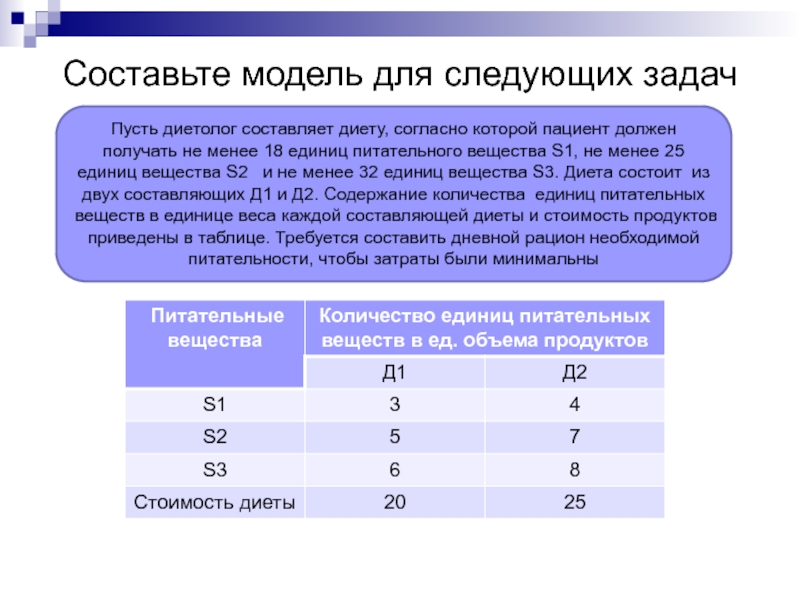
Слайд 38Составьте модель для следующих задач
Пусть диетолог составляет диету, согласно которой пациент
Слайд 39Задача о раскрое
Строительная фирма заказала изготовить заготовки двух видов: 2 м
Каждая доска длиной 5 м может быть распилена несколькими способами:
На 2 заготовки по 2 м;
на 1 заготовку длиной 2 м и две заготовки 1,5 м;
На 3 заготовки по 1,5 м.
Отходы должны быть минимальные
Целевая функция:
F=Х1+X2 + Х3→ min
Слайд 40Транспортная задача
На двух складах А1 и А2 имеется соответственно 11 и
10
8
7
11
14
Целевая функция
F=8X11+6X12+5X13+4X21+5X22+7X23→min
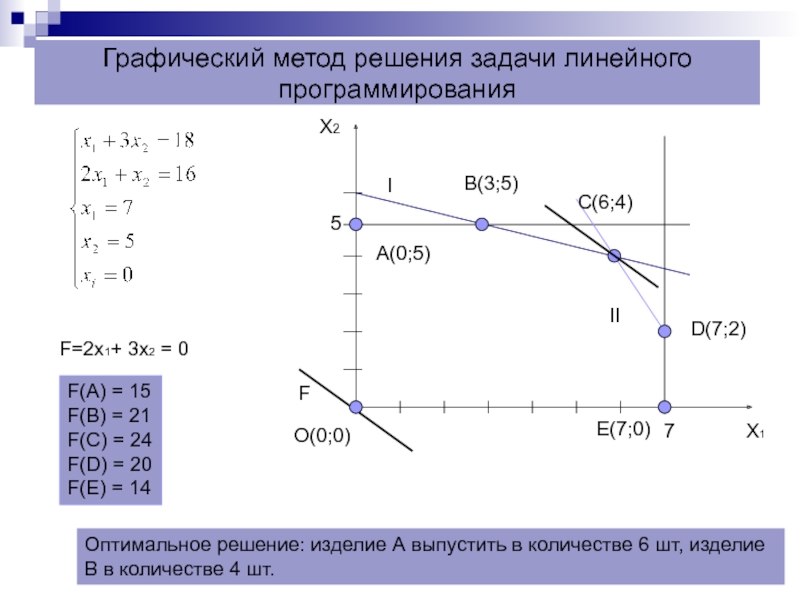
Слайд 41Графический метод решения задачи линейного программирования
Х1
Х2
I
II
7
5
F
F=2x1+ 3x2 = 0
A(0;5)
B(3;5)
C(6;4)
D(7;2)
E(7;0)
O(0;0)
F(A) = 15
F(B)
F(C) = 24
F(D) = 20
F(E) = 14
Оптимальное решение: изделие А выпустить в количестве 6 шт, изделие
В в количестве 4 шт.