- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Виды четырехугольников. презентация
Содержание
- 1. Виды четырехугольников.
- 2. Параллелограмм. Параллелограммом Называется четырехугольник, у которого противолежащие стороны попарно параллельны.
- 3. Свойства параллелограмма: противолежащие стороны равны; противоположные углы
- 4. Признаки параллелограмма. Четырехугольник является параллелограммом, если: Две
- 5. Трапеция. Трапецией называется четырехугольник, у которого две
- 6. Свойства трапеции: ее средняя линия параллельна основаниям
- 7. Прямоугольник. Прямоугольником называется параллелограмм, у которого все углы прямые.
- 8. Свойства прямоугольника: все свойства параллелограмма; диагонали равны.
- 9. Ромб. Ромбом называется параллелограмм, у которого все стороны равны.
- 10. Свойства ромба: все свойства параллелограмма; диагонали перпендикулярны; диагонали являются биссектрисами его углов.
- 11. Признаки ромба. Параллелограмм является ромбом, если: Две
- 12. Квадрат. Квадратом называется прямоугольник, у которого все стороны равны.
- 13. Свойства квадрата: все углы квадрата прямые; диагонали
- 14. Признаки квадрата. Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.
- 15. Основные формулы: Параллелограмм. a и b —
- 16. Трапеция. a и b — основания; h
- 17. Ромб. S = aha S = a2sin
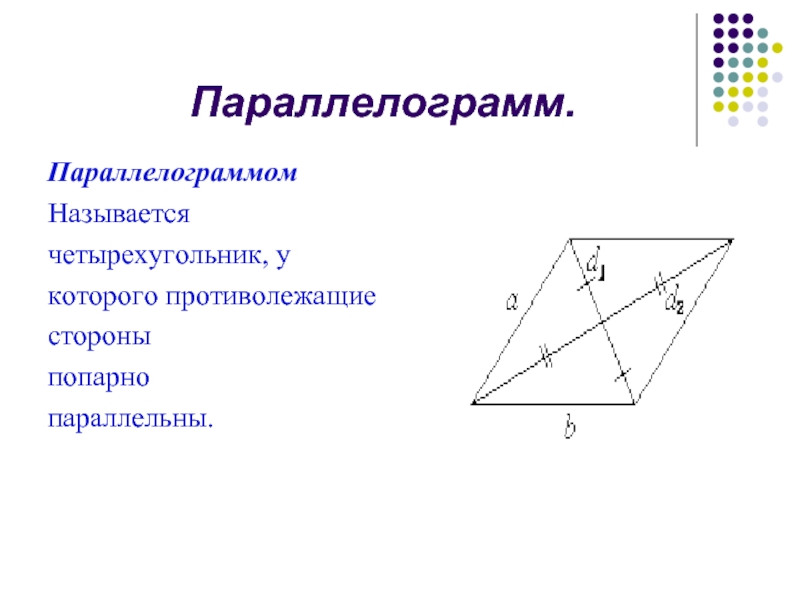
Слайд 2Параллелограмм.
Параллелограммом
Называется
четырехугольник, у
которого противолежащие
стороны
попарно
параллельны.
Слайд 3Свойства параллелограмма:
противолежащие стороны равны;
противоположные углы равны;
диагонали точкой пересечения делятся пополам;
сумма углов,
прилежащих к одной стороне, равна 180°;
сумма квадратов диагоналей равна сумме квадратов всех сторон
сумма квадратов диагоналей равна сумме квадратов всех сторон
Слайд 4Признаки параллелограмма.
Четырехугольник является
параллелограммом, если:
Две его противоположные стороны равны и параллельны.
Противоположные стороны
попарно равны.
Противоположные углы попарно равны.
Диагонали точкой пересечения делятся пополам.
Противоположные углы попарно равны.
Диагонали точкой пересечения делятся пополам.
Слайд 5Трапеция.
Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две
другие непараллельны.
Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами.
Отрезок, соединяющий середины боковых сторон, называется средней линией.
Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной.
Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами.
Отрезок, соединяющий середины боковых сторон, называется средней линией.
Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной.
Слайд 6Свойства трапеции:
ее средняя линия параллельна основаниям и равна их полусумме;
если трапеция
равнобедренная, то ее диагонали равны и углы при основании равны;
если трапеция равнобедренная, то около нее можно описать окружность;
если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
если трапеция равнобедренная, то около нее можно описать окружность;
если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
Слайд 10Свойства ромба:
все свойства параллелограмма;
диагонали перпендикулярны;
диагонали являются биссектрисами его углов.
Слайд 11Признаки ромба.
Параллелограмм является ромбом, если:
Две его смежные стороны равны.
Его диагонали перпендикулярны.
Одна
из диагоналей является биссектрисой его угла.
Слайд 13Свойства квадрата:
все углы квадрата прямые;
диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения
делятся пополам и делят углы квадрата пополам
Слайд 14Признаки квадрата.
Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.
Слайд 15Основные формулы:
Параллелограмм.
a и b — смежные стороны; — угол между ними;
ha — высота, проведенная к стороне a.
S = aha
S = ab sin
S =d1d2 sin
S = aha
S = ab sin
S =d1d2 sin
Слайд 16Трапеция.
a и b — основания; h — расстояние между ними; l
— средняя линия.
S = lh
S = lh
Прямоугольник.
S = ab
S = d1d2 sin