- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
векторы презентация
Содержание
- 1. векторы
- 2. А Нулевой вектор
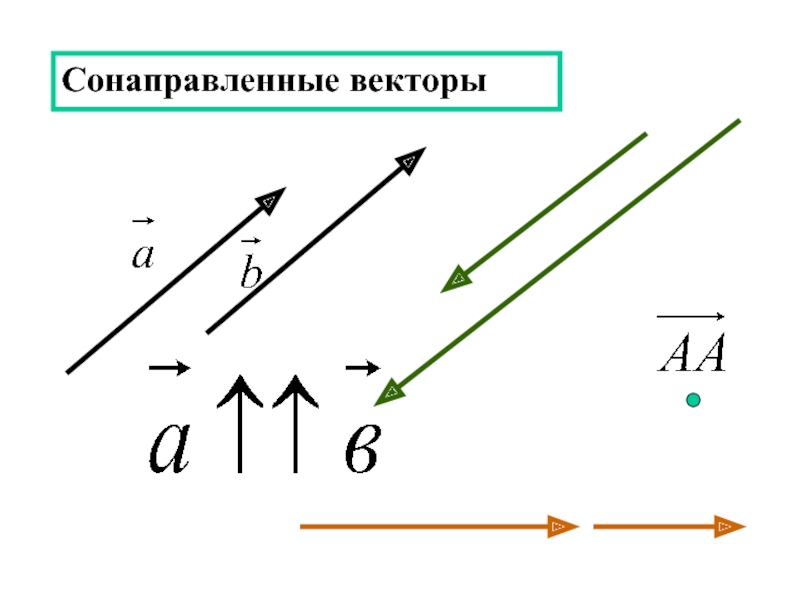
- 3. Сонаправленные векторы
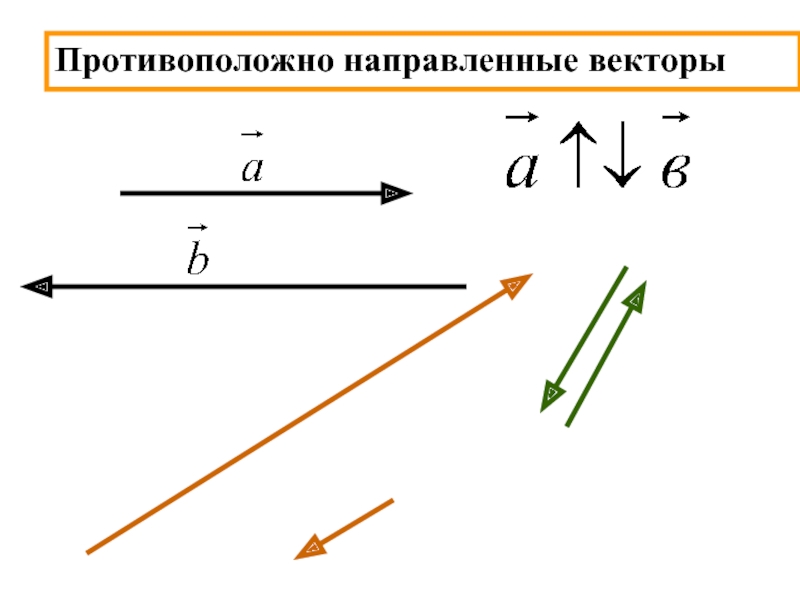
- 4. Противоположно направленные векторы
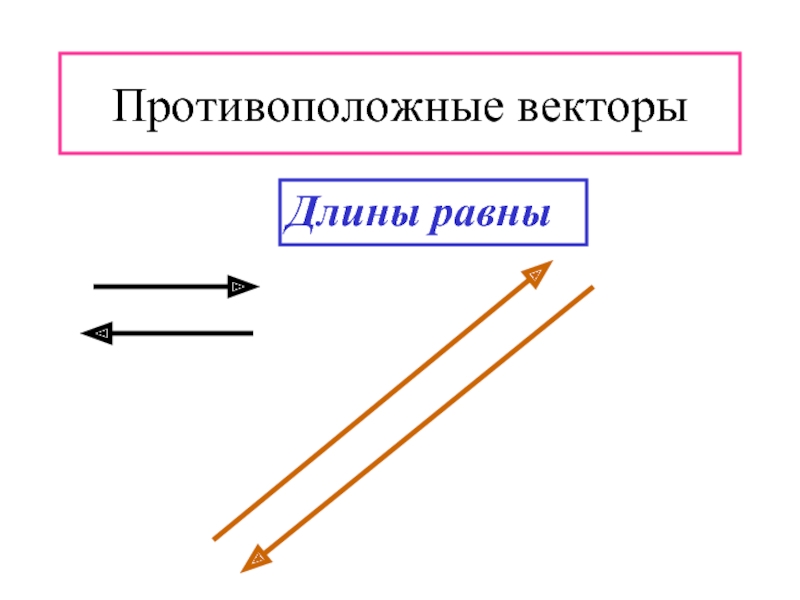
- 5. Противоположные векторы Длины равны
- 6. Коллинеарные векторы Два ненулевых вектора называются коллинеарными,
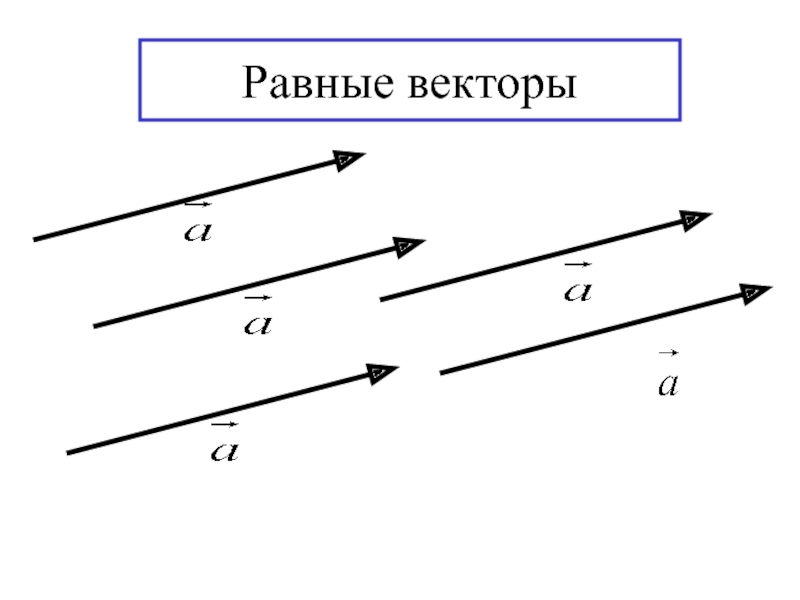
- 7. Равные векторы
- 8. Векторы называются равными, если они сонаправлены и их длины равны.
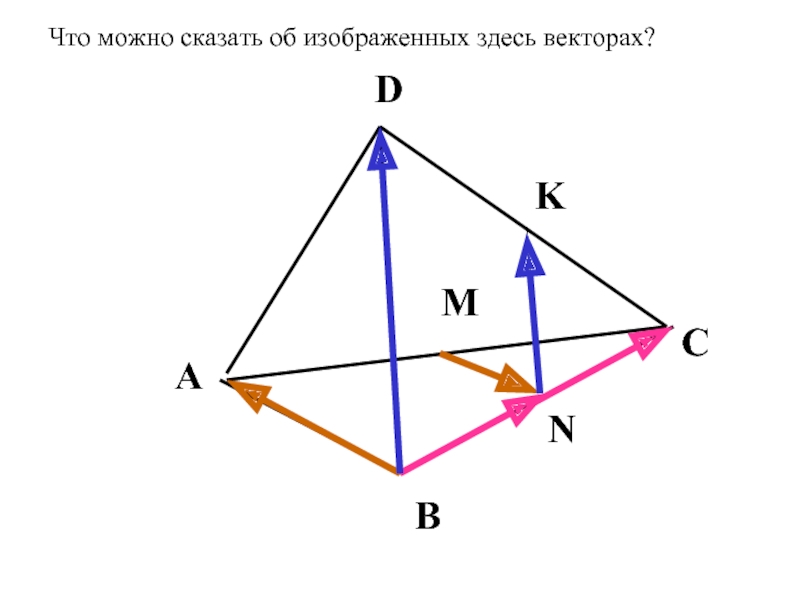
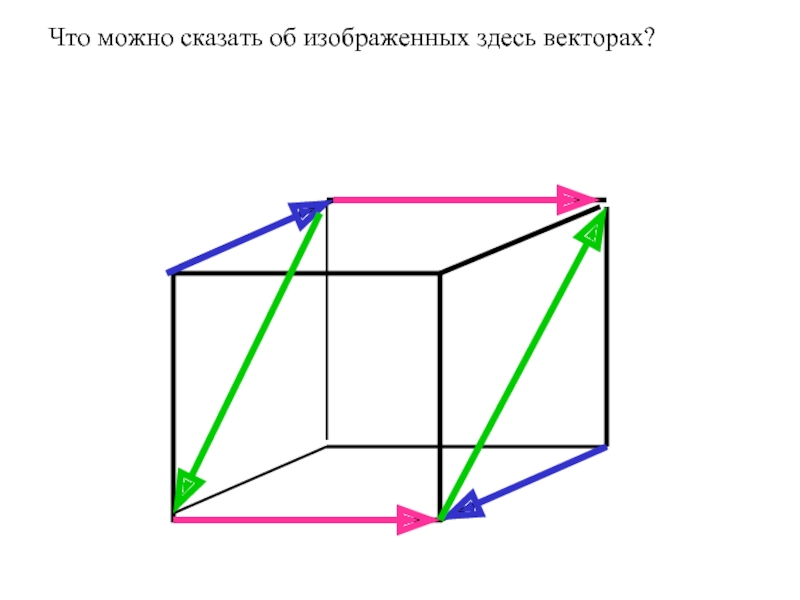
- 9. K N D С В А M Что можно сказать об изображенных здесь векторах?
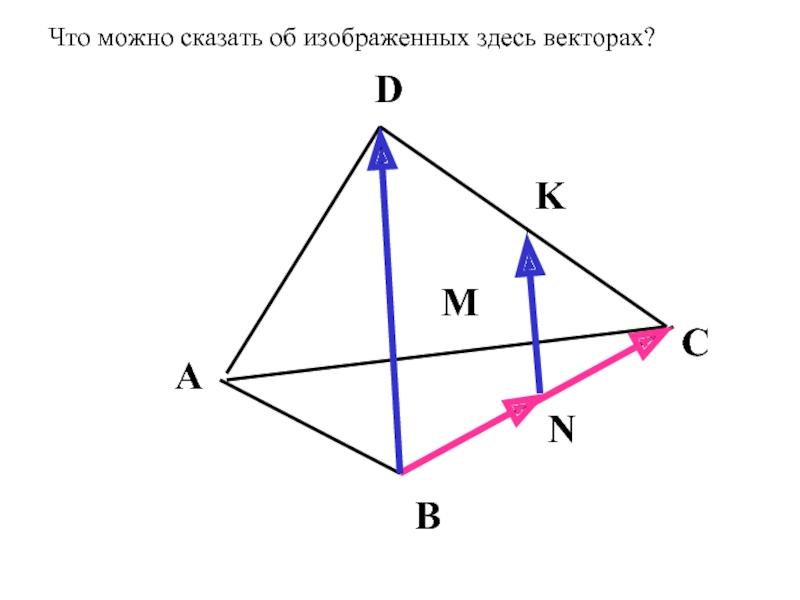
- 10. K N D С В А M Что можно сказать об изображенных здесь векторах?
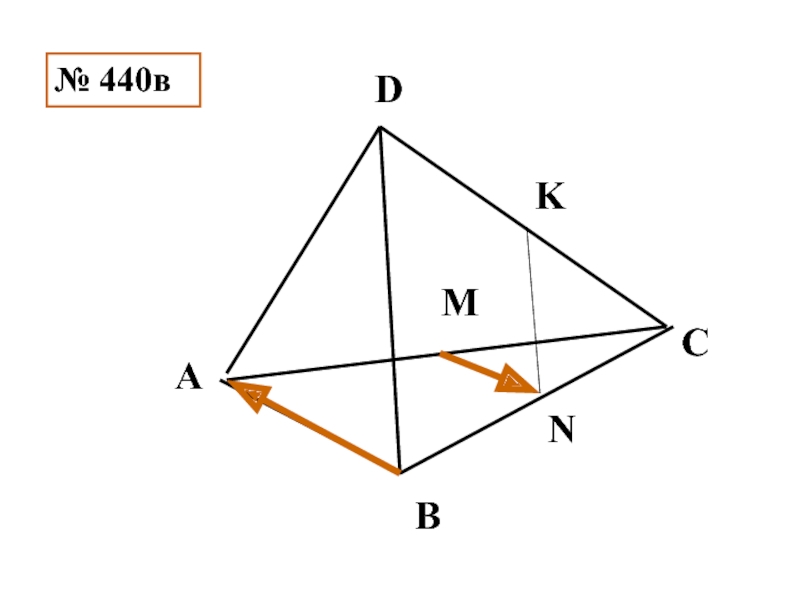
- 11. № 440в K N D С В А M
- 12. Что можно сказать об изображенных здесь векторах?
- 13. Действия над векторами: сложение
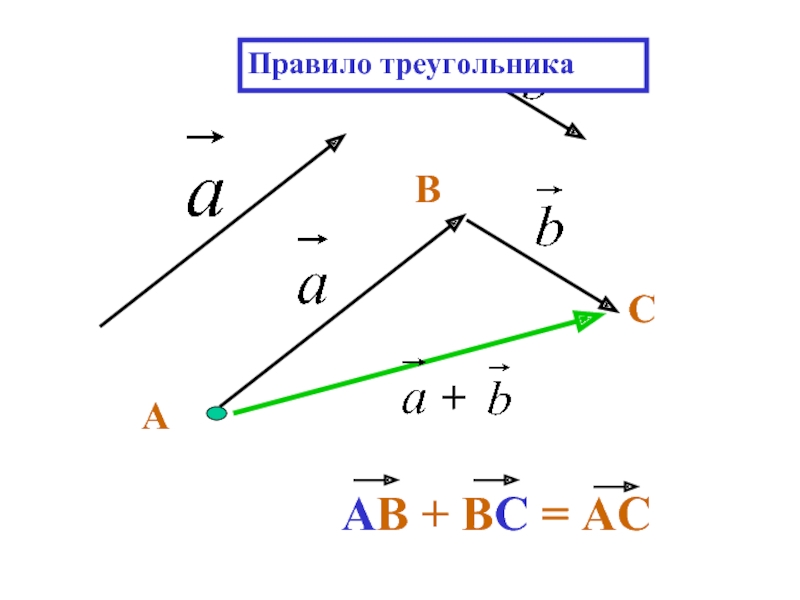
- 14. + АВ + ВС = АС
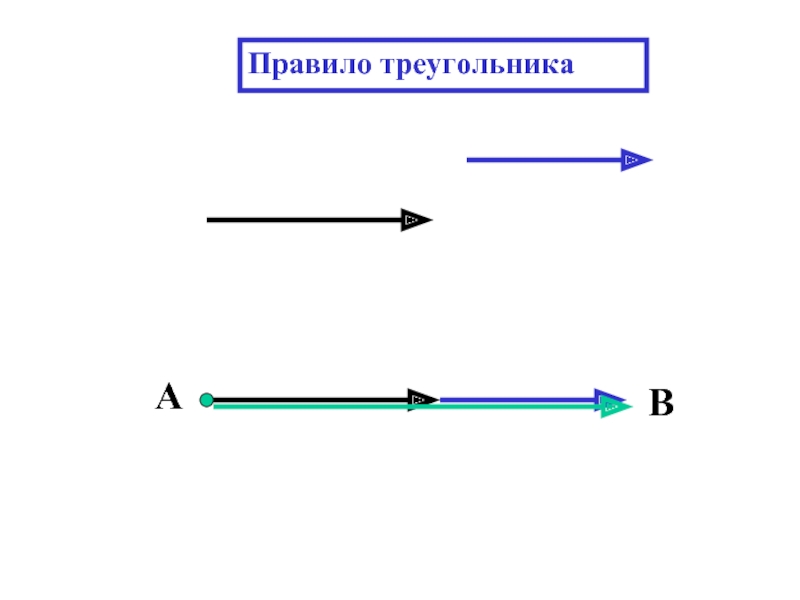
- 15. А В Правило треугольника
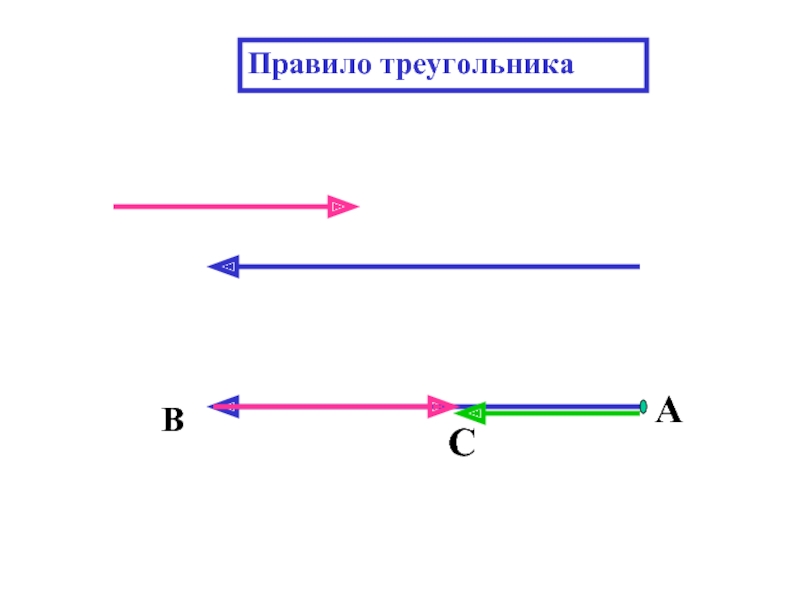
- 16. Правило треугольника А С В
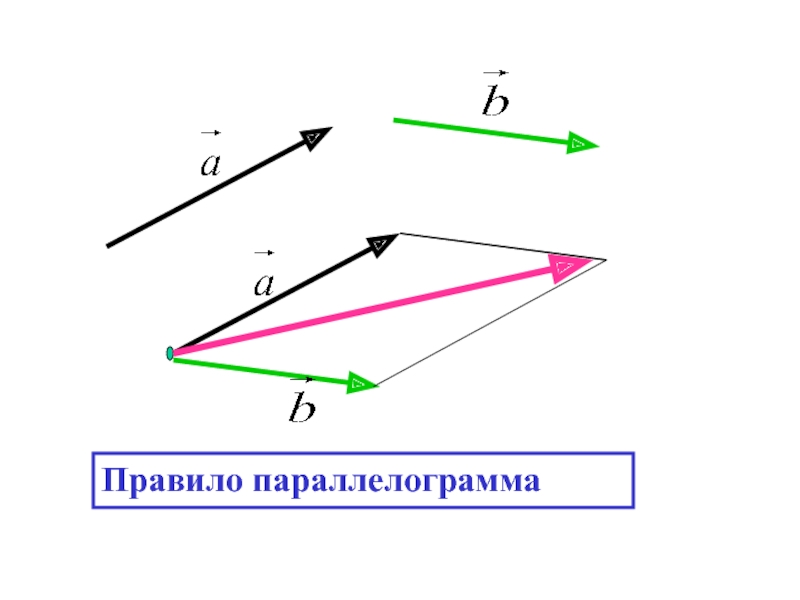
- 17. Правило параллелограмма
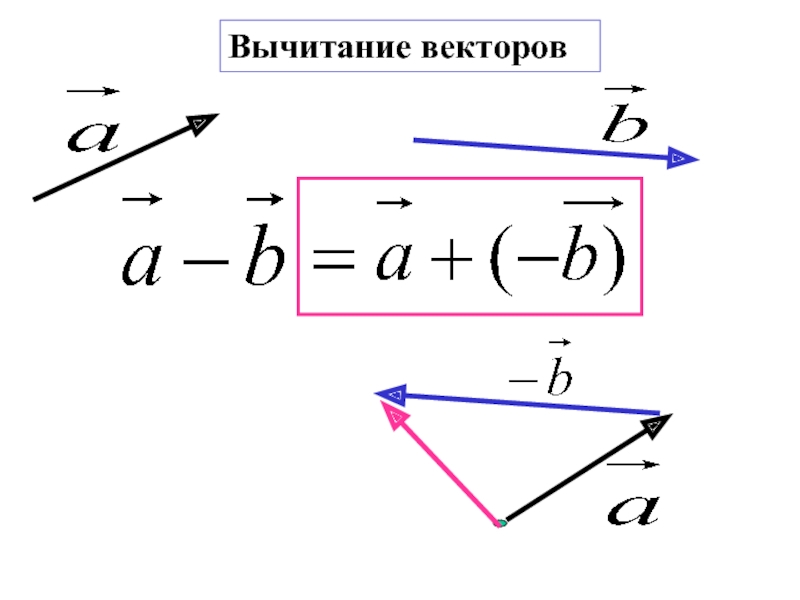
- 18. Вычитание векторов
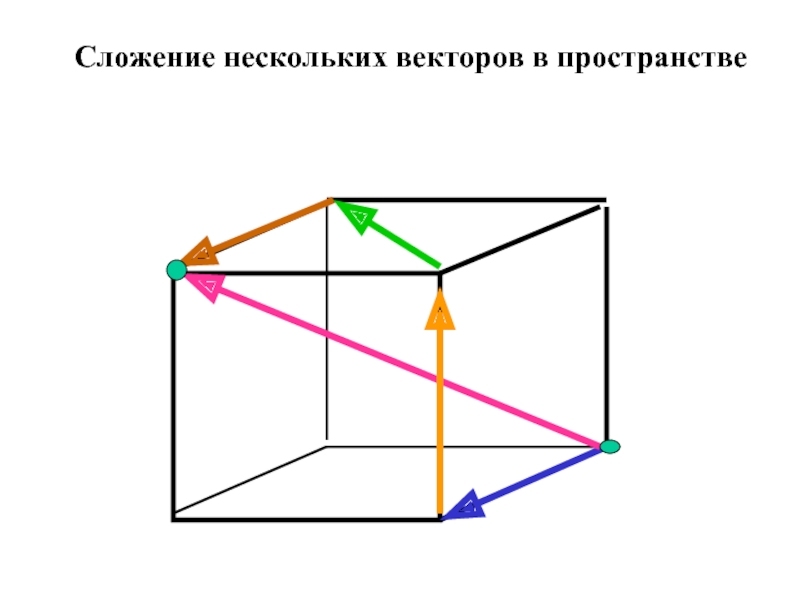
- 19. Сложение нескольких векторов в пространстве
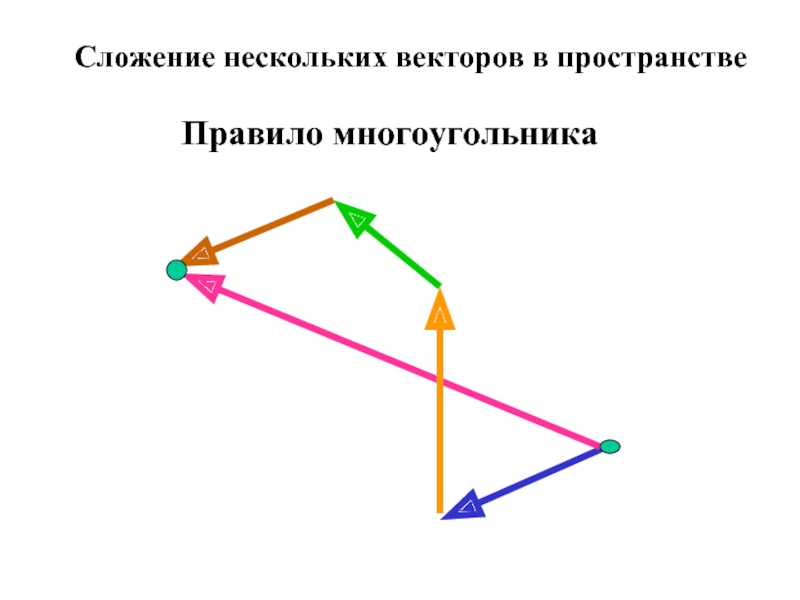
- 20. Сложение нескольких векторов в пространстве Правило многоугольника
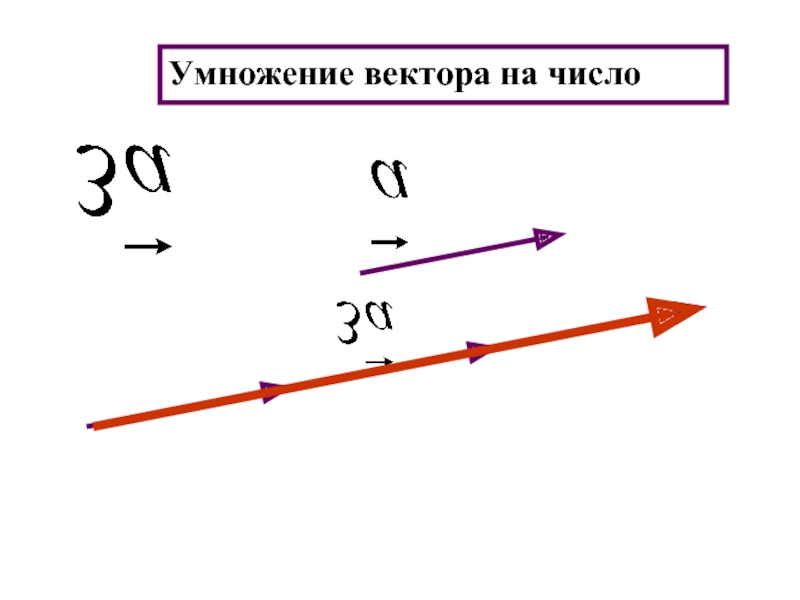
- 21. Умножение вектора на число
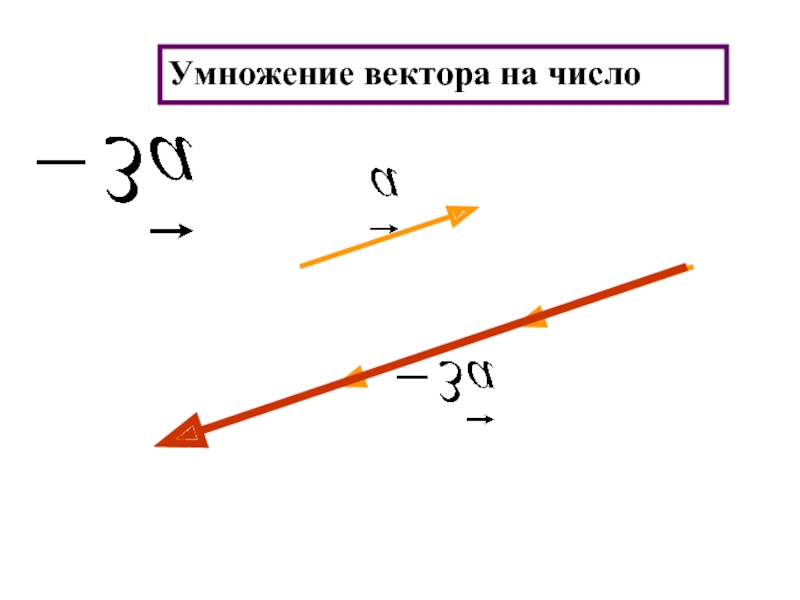
- 22. Умножение вектора на число
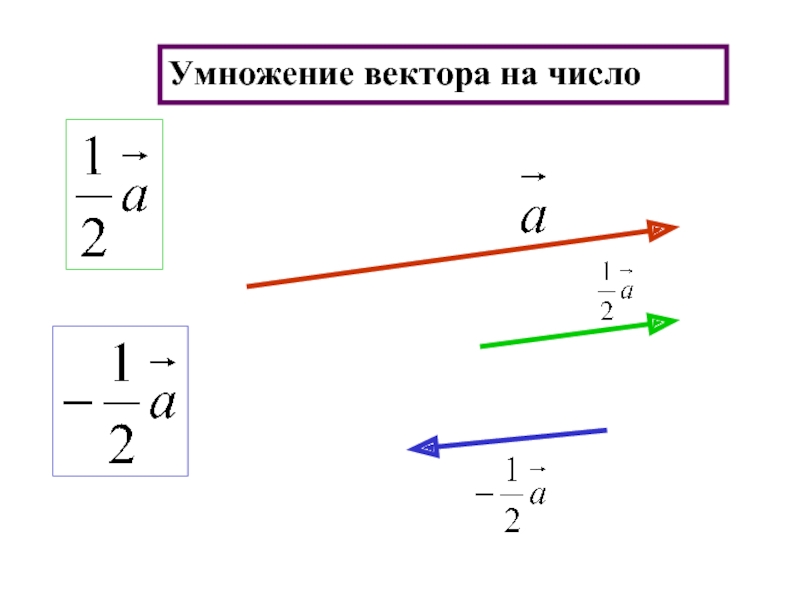
- 23. Умножение вектора на число
- 24. Умножение вектора на число
- 25. Произведением ненулевого вектора а на число
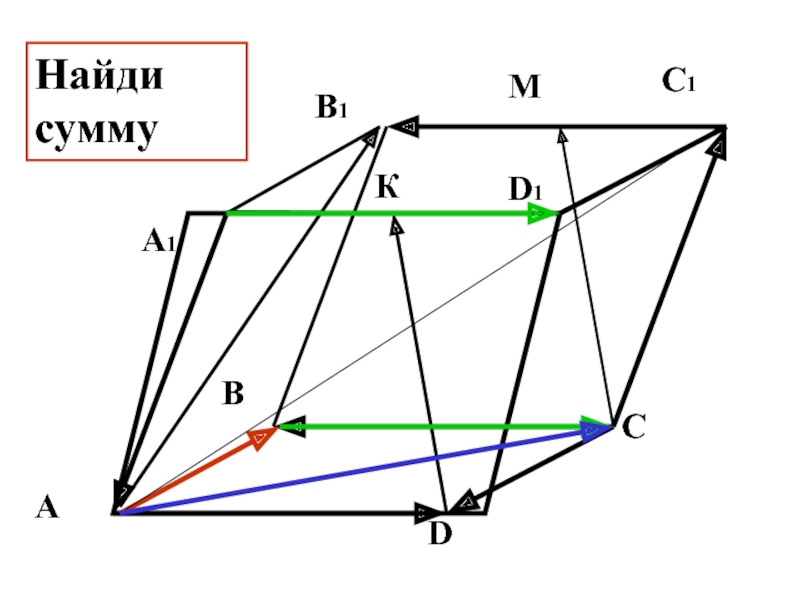
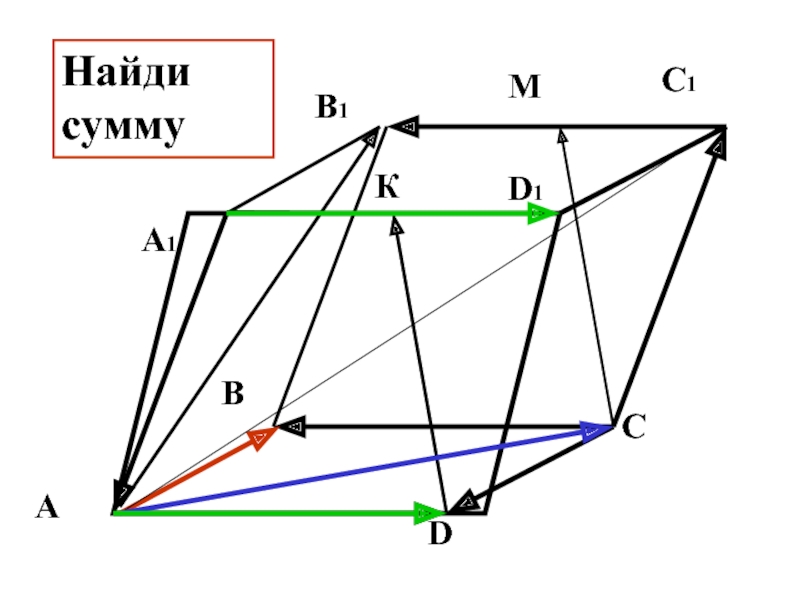
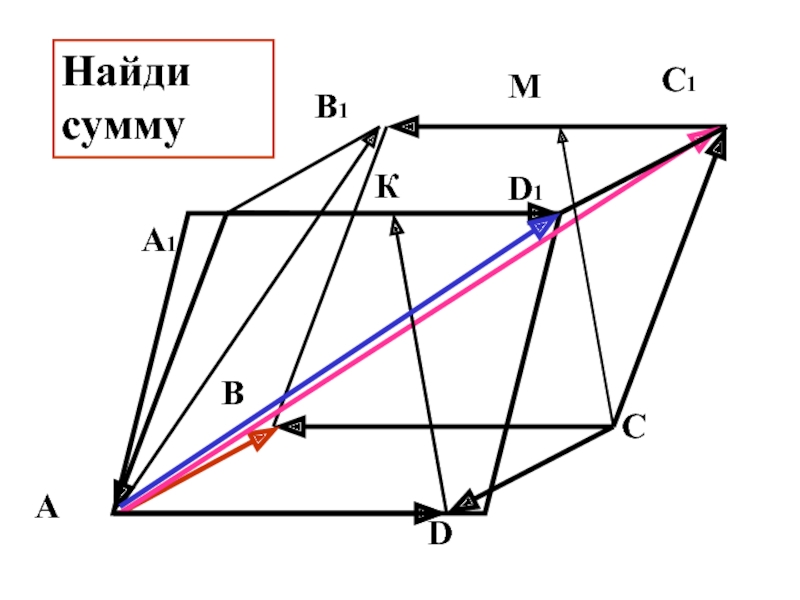
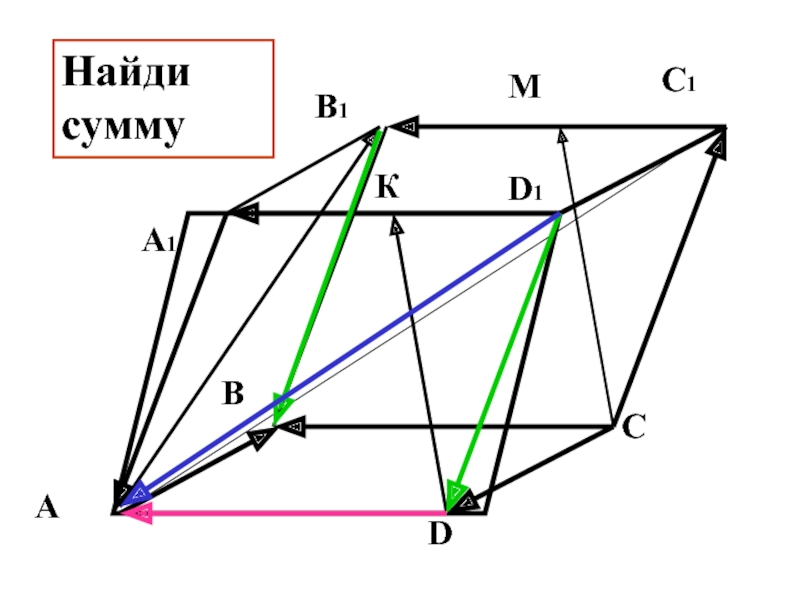
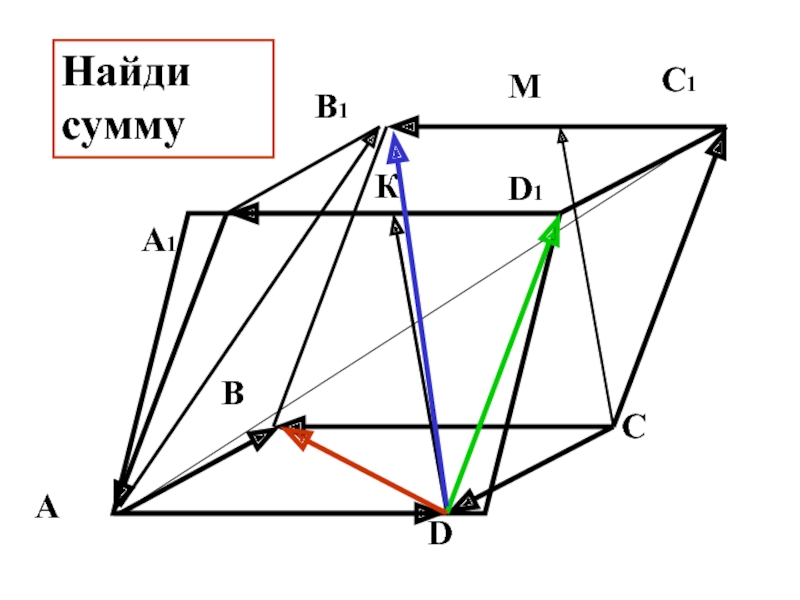
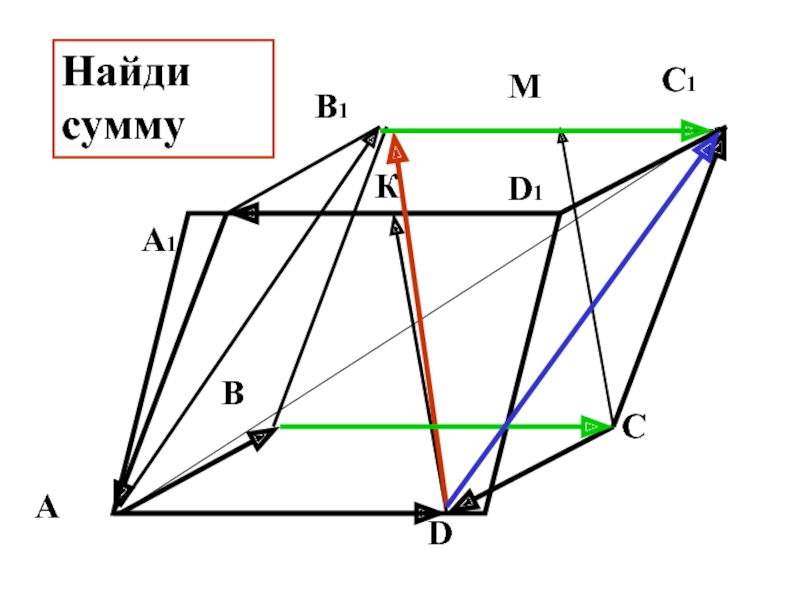
- 26. В С D А D1 С1 В1 А1 М К Найди сумму
- 27. В С D А D1 С1 В1 А1 М К Найди сумму
- 28. В С D А D1 С1 В1 А1 М К Найди сумму
- 29. В С D А D1 С1 В1 А1 М К Найди сумму
- 30. В С D А D1 С1 В1 А1 М К Найди сумму
- 31. В С D А D1 С1 В1 А1 М К Найди сумму
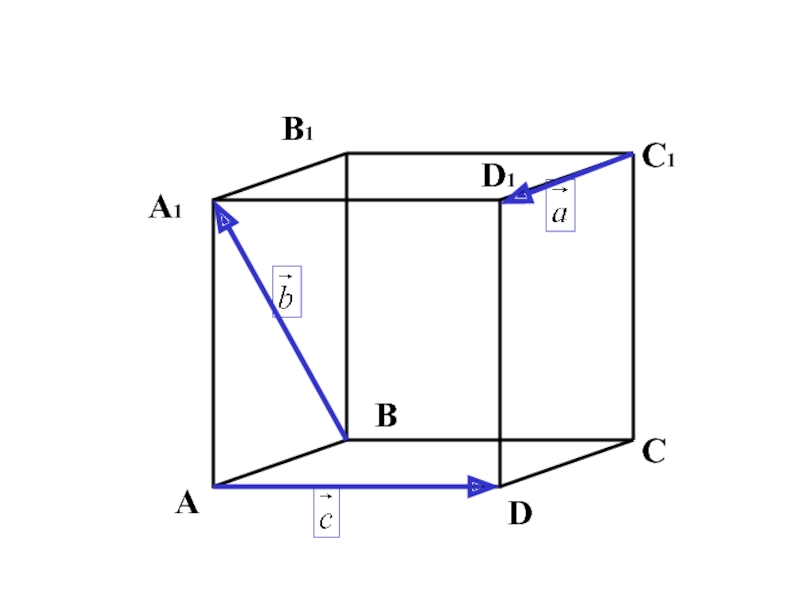
- 32. В C D А А1 D1 С1 В1
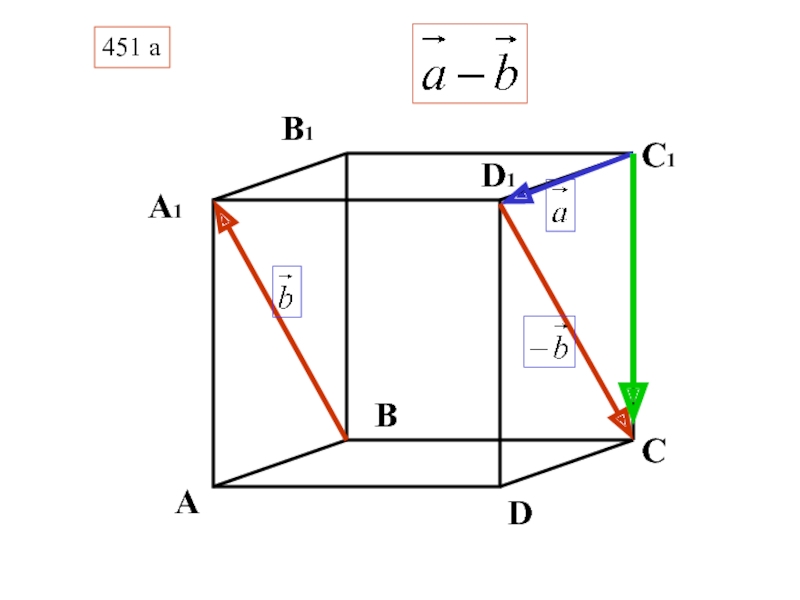
- 33. В C D А А1 D1 С1 В1 451 а
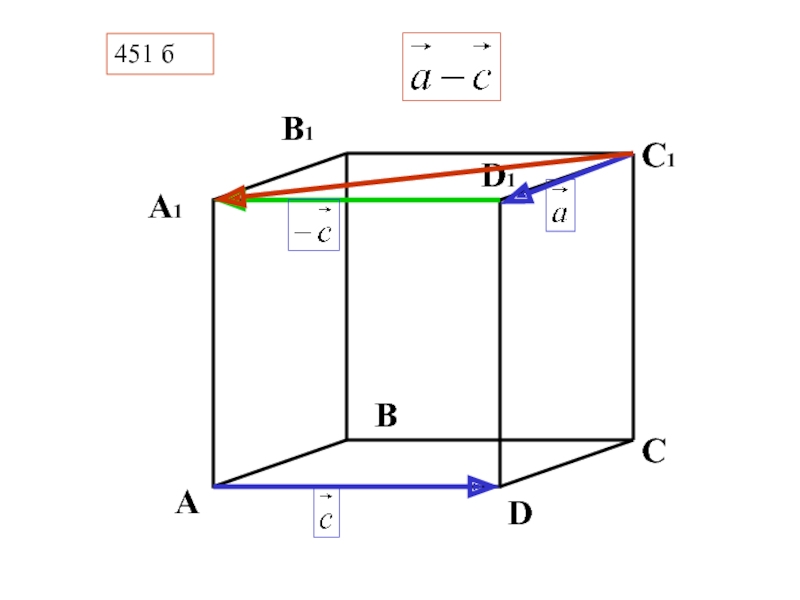
- 34. В C D А А1 D1 С1 В1 451 б
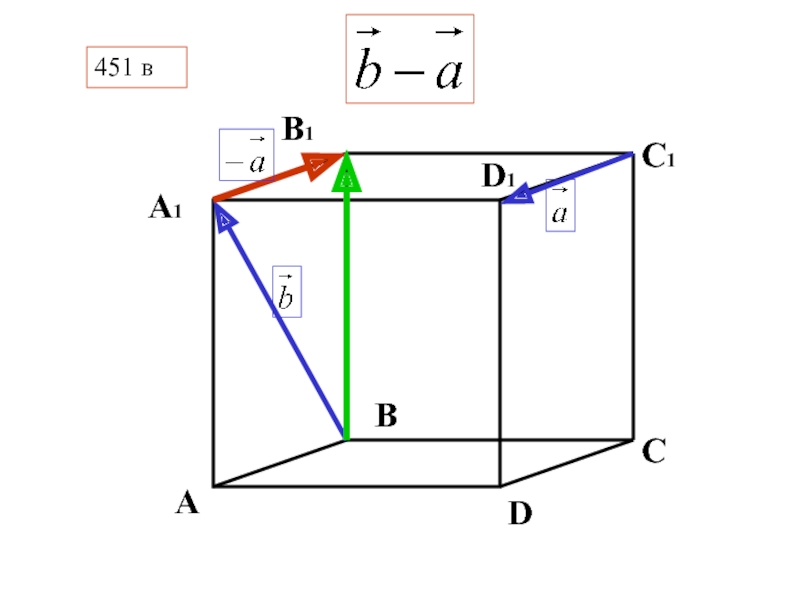
- 35. В C D А А1 D1 С1 В1 451 в
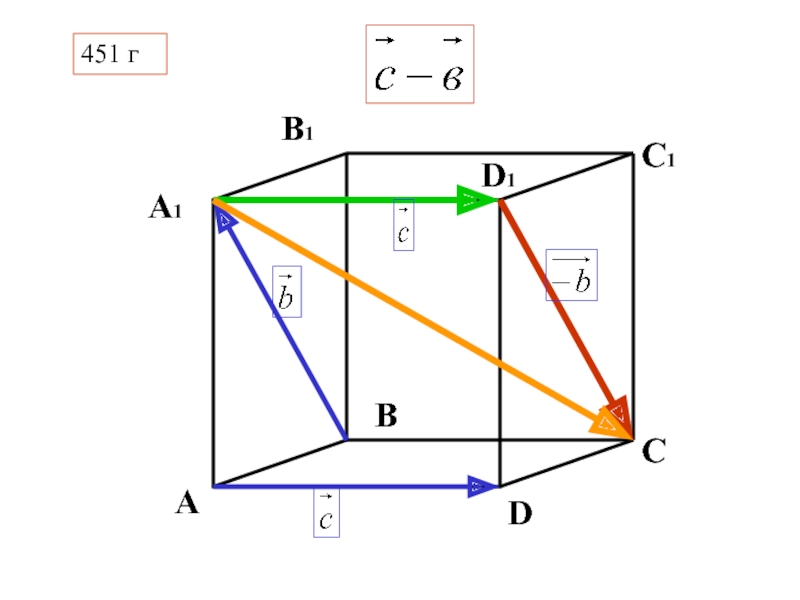
- 36. В C D А А1 D1 С1 В1 451 г
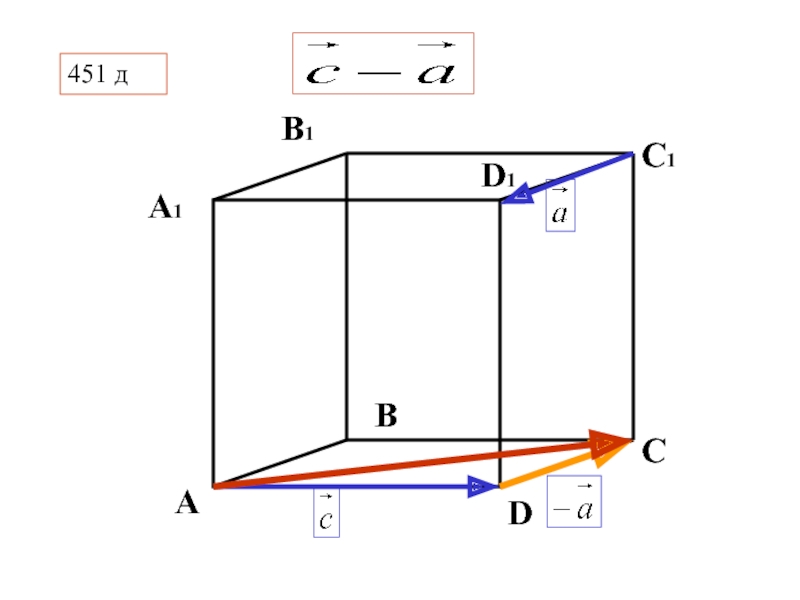
- 37. В C D А А1 D1 С1 В1 451 д
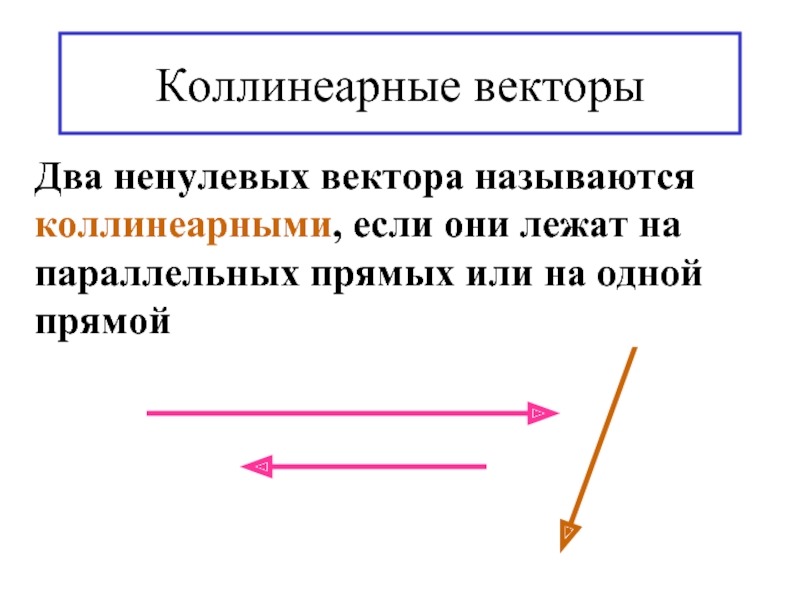
Слайд 6Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если они лежат на параллельных
прямых или на одной прямой
Слайд 25Произведением ненулевого вектора а на число к называется вектор в
:
1) длина которого равна длине вектора а, умноженной на | к |
2) если к 0, то векторы а и в сонаправлены
если к < 0, то векторы а и в противоположно направлены
1) длина которого равна длине вектора а, умноженной на | к |
2) если к 0, то векторы а и в сонаправлены
если к < 0, то векторы а и в противоположно направлены