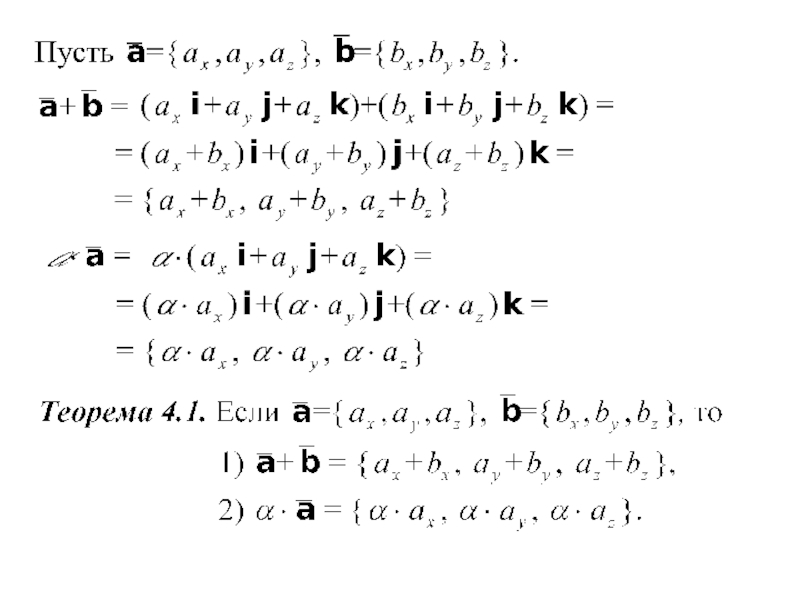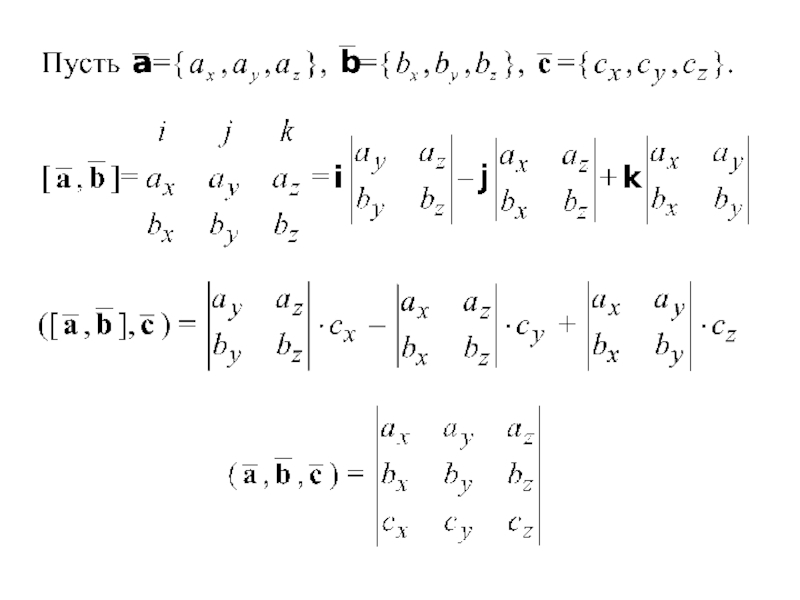- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторная алгебра презентация
Содержание
- 1. Векторная алгебра
- 2. Определение. Вектором или по-другому свободным вектором называется
- 3. Под углом между векторами
- 4. Определение. Произведением вектора на
- 5. Определение. Суммой векторов и называется
- 7. Свойства линейных операций над векторами 4. 1.
- 13. Пусть – произвольный вектор. Тогда или
- 15. Свойства проекций: 1. 2. 3.
- 19. Пример
- 21. – невозможно
- 24. Свойства скалярного произведения 4. 1. 2. 3.
- 27. Свойства векторного произведения 4. 1. 2. 3.
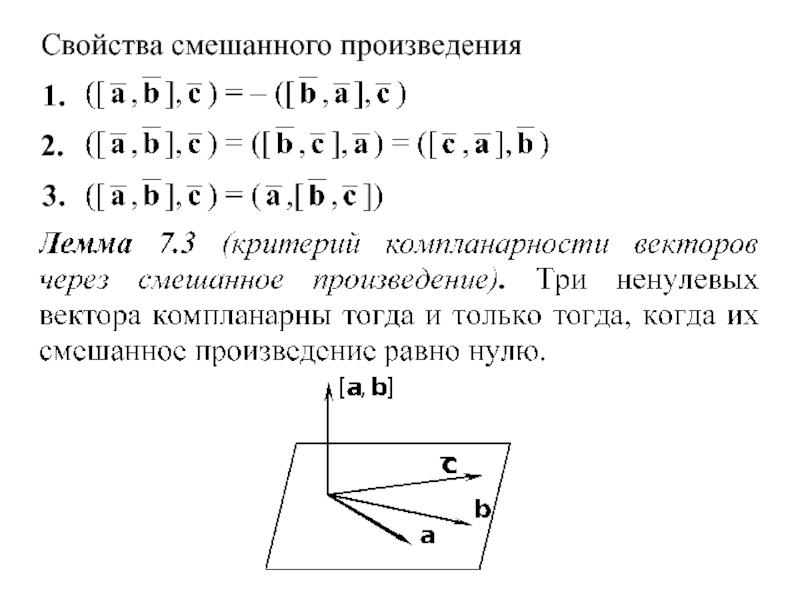
- 32. Свойства смешанного произведения 1. 2. 3.
Слайд 1Векторная алгебра
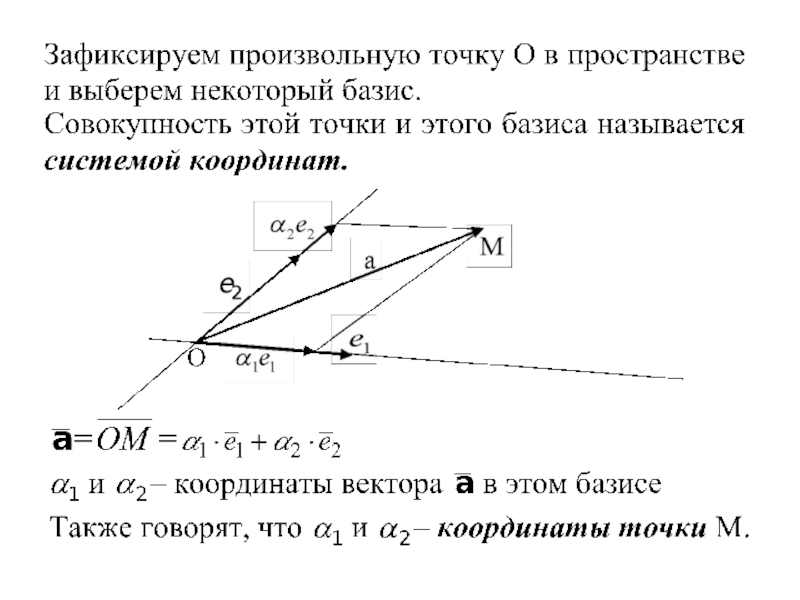
Разложение вектора по базису
Системы координат
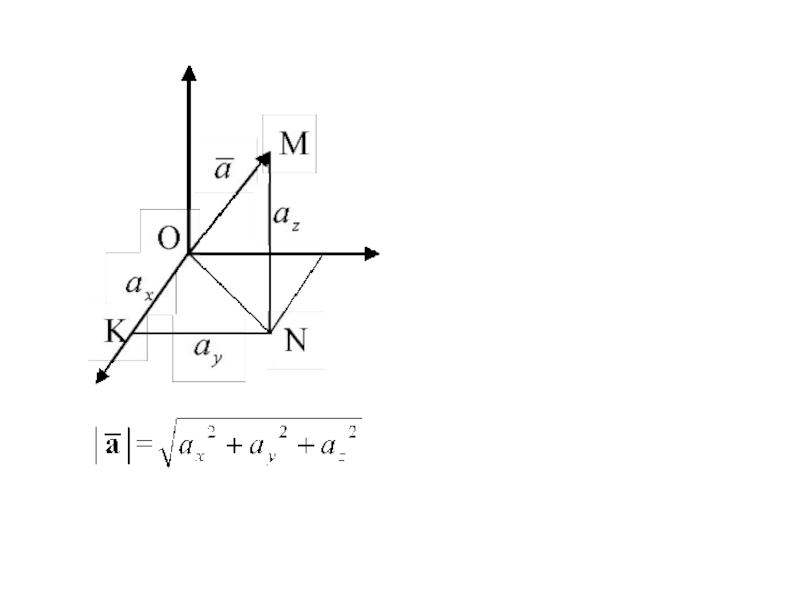
Декартова прямоугольная система
Скалярное произведение векторов
Свойства скалярного произведения
Векторное произведение
Смешанное произведение
Свойства смешанного произведения
Слайд 2Определение. Вектором или по-другому свободным вектором называется направленный отрезок (т.е. отрезок,
Расстояние от начала вектора до его конца называется длиной (модулем) вектора.
Вектор, длина которого равна единице, называется единичным вектором или ортом.
Вектор, начало и конец которого совпадают, называ-ется нулевым и обозначается . Нулевой вектор не имеет определенного направления и имеет длину, равную нулю.
Слайд 3Под углом между векторами и
Два вектора и называются ортогональными, если угол между ними равен 900.
Два вектора и называются коллинеарными, если они лежат на одной или параллельных прямых.
Три вектора, лежащие в одной или в параллельных плоскостях, называются компланарными.
Два вектора называются равными, если они сона-правлены и имеют одинаковую длину. Все нулевые векторы считаются равными.
Слайд 4Определение. Произведением вектора на число
при и противоположно ему при . Если
или , то их произведение полагают рав-ным .
=
противоположный вектору
Лемма 2.1 (критерий коллинеарности векторов). Два ненулевых вектора и коллинеарны тогда и только тогда, когда , для некоторого числа .
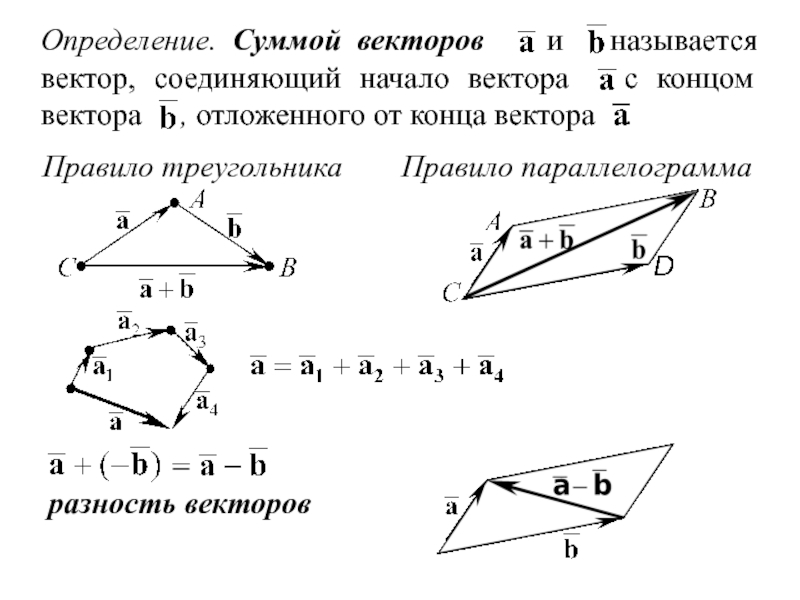
Слайд 5Определение. Суммой векторов и называется вектор, соединяющий начало вектора
Правило треугольника
Правило параллелограмма
=
разность векторов