- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок 15 презентация
Содержание
- 1. Урок 15
- 2. Два равнобедренных треугольника АВС (\АВ\ = \АС\)
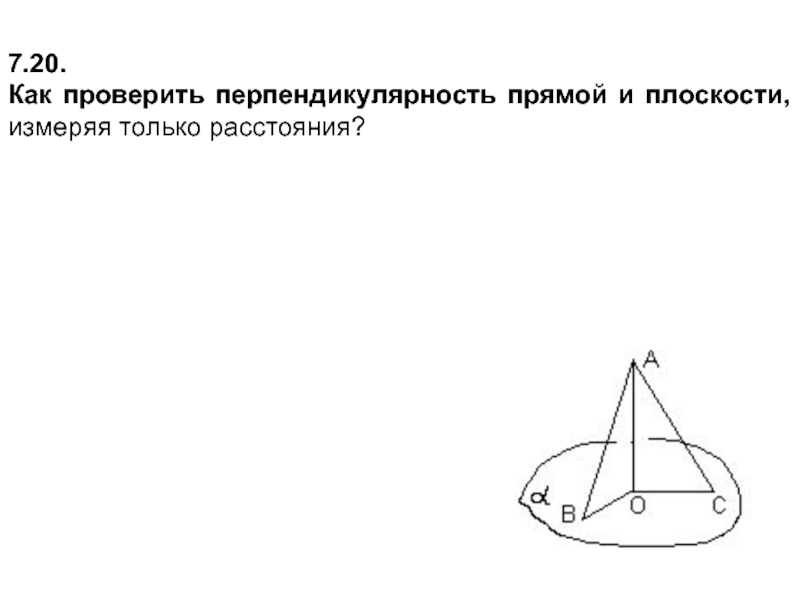
- 3. 7.20. Как проверить перпендикулярность прямой и плоскости, измеряя только расстояния?
- 4. Объясните, как через данную точку пространства провести перпендикуляр к данной прямой 2 случая)
- 5. Задача о построении плоскости, перпендикулярной данной
- 6. Итак, во - первых, доказано существование
- 7. Доказательство. Пусть А∈a. Тогда ∃!α |
- 8. Плоскость, проходящая через данную точку данной
- 9. Пусть АВСОА1В1С1D1— куб. Нарисуйте его сечение
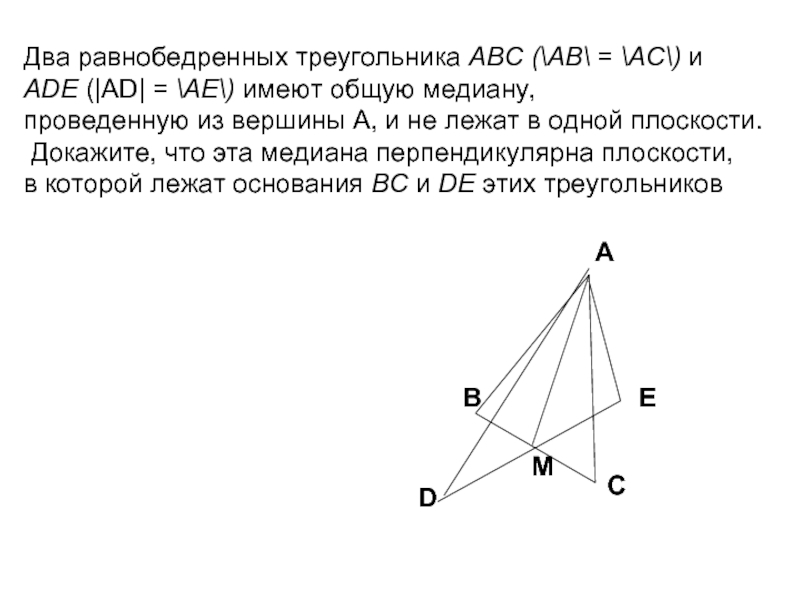
Слайд 2Два равнобедренных треугольника АВС (\АВ\ = \АС\) и
АDЕ (|AD| =
проведенную из вершины A, и не лежат в одной плоскости.
Докажите, что эта медиана перпендикулярна плоскости,
в которой лежат основания ВС и DЕ этих треугольников
А
В
С
D
E
M
Слайд 4Объясните, как через данную точку
пространства провести перпендикуляр к данной прямой
2 случая)
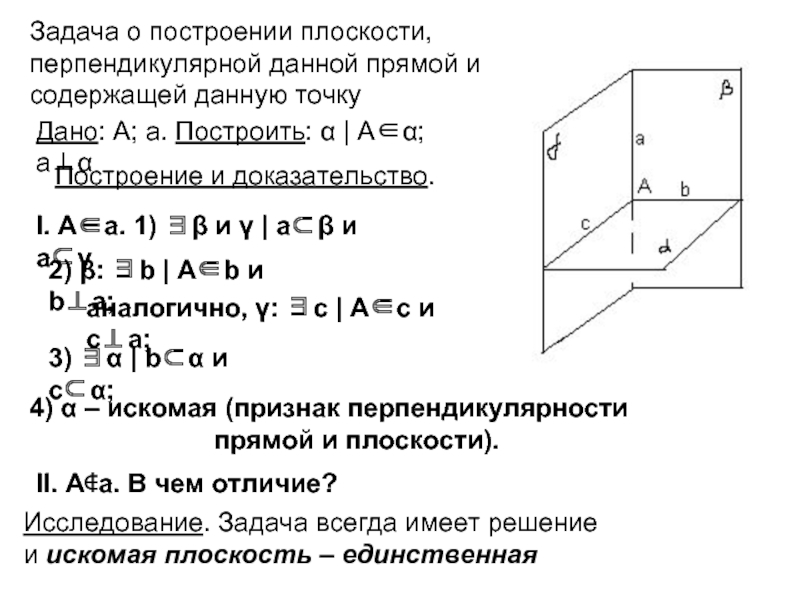
Слайд 5Задача о построении плоскости,
перпендикулярной данной прямой и
содержащей данную точку
Дано: А; а. Построить: α | A∈α; a⊥α
Построение и доказательство.
I. A∈а. 1) ∃β и γ | a⊂β и a⊂γ
2) β: ∃b | A∈b и b⊥a;
аналогично, γ: ∃c | A∈c и c⊥a;
3) ∃α | b⊂α и c⊂α;
4) α – искомая (признак перпендикулярности
прямой и плоскости).
II. A∉а. В чем отличие?
Исследование. Задача всегда имеет решение
и искомая плоскость – единственная
Слайд 6Итак,
во - первых, доказано существование перпендикулярных прямой и плоскости,
а,
через данную точку можно провести плоскость, перпендикулярную данной прямой и только одну.
Эта теорема имеет важное следствие:
прямые, перпендикулярные данной прямой
в данной ее точке, лежат в одной плоскости
и покрывают ее.
(Плоскость является геометрическим местом таких прямых)
Слайд 7Доказательство.
Пусть А∈a. Тогда ∃!α | A∈α и a⊥α.
∀X∈α a⊥(XA)
поэтому плоскость покрыта прямыми, перпендикулярными а.
2) Пусть ∃b | b⊥a и b⊄α, тогда ∃β | a⊂β и b⊂β, причем β α = c.
Значит, в плоскости β через точку А проходят
два перпендикуляра к прямой а: b и с, что невозможно
Прямые, перпендикулярные данной прямой
в данной ее точке, лежат в одной плоскости
и покрывают ее.
Слайд 8Плоскость, проходящая через данную точку
данной прямой и перпендикулярная к ней,
называется плоскостью перпендикуляров.
Слайд 9Пусть АВСОА1В1С1D1— куб.
Нарисуйте его сечение плоскостью,
проходящей через вершину А
а) (ВD); б) (B1D1; в) (СD1); г) (АD1); д) (АС);
е) (C1D); ж) (В1D).