- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Углы и отрезки, связанные с окружностью. презентация
Содержание
- 1. Углы и отрезки, связанные с окружностью.
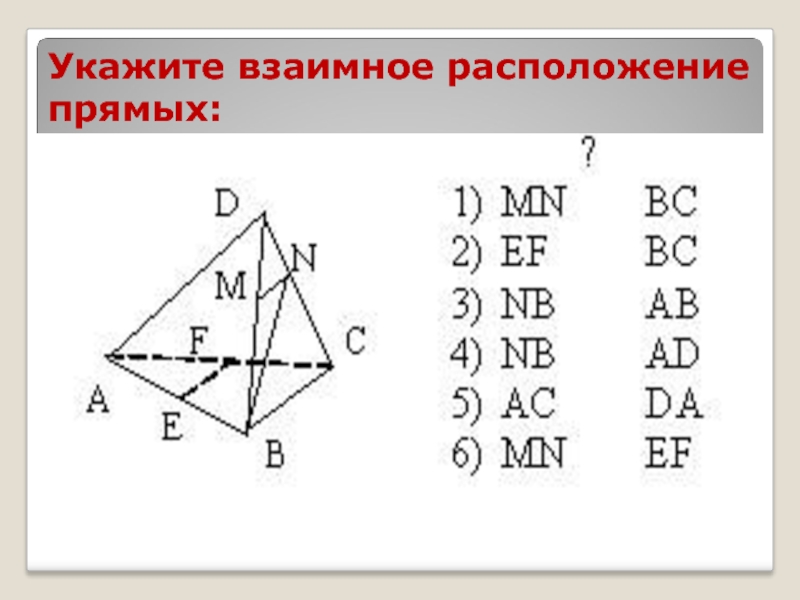
- 2. Укажите взаимное расположение прямых:
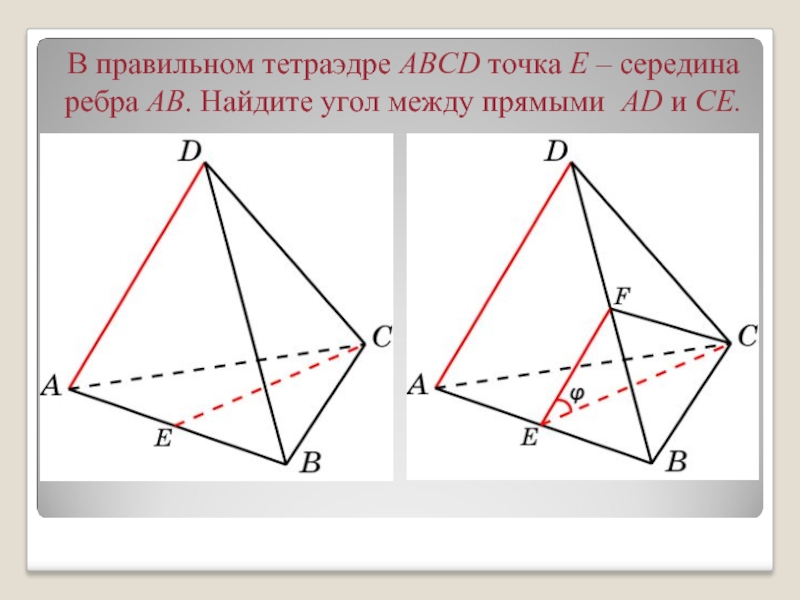
- 3. В правильном тетраэдре ABCD точка E –
- 4. Углы и отрезки, связанные с окружностью. Основные понятия: 1.Касательная. Свойства касательной.
- 5. Углы и отрезки, связанные с окружностью. Основные
- 6. Свойства окружности: Прямая может
- 7. Теорема о касательной и секущей
- 8. Теорема о секущих: Если из точки, лежащей
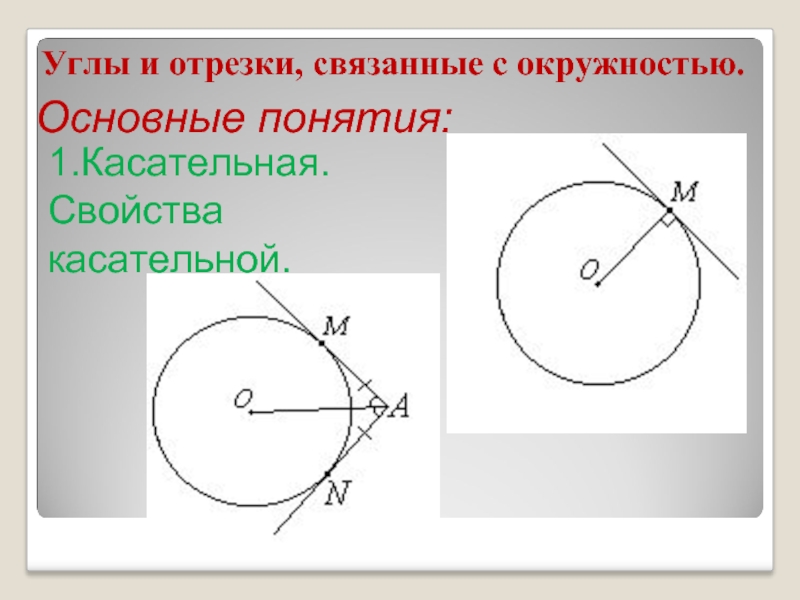
Слайд 4Углы и отрезки, связанные с окружностью.
Основные понятия:
1.Касательная. Свойства касательной.
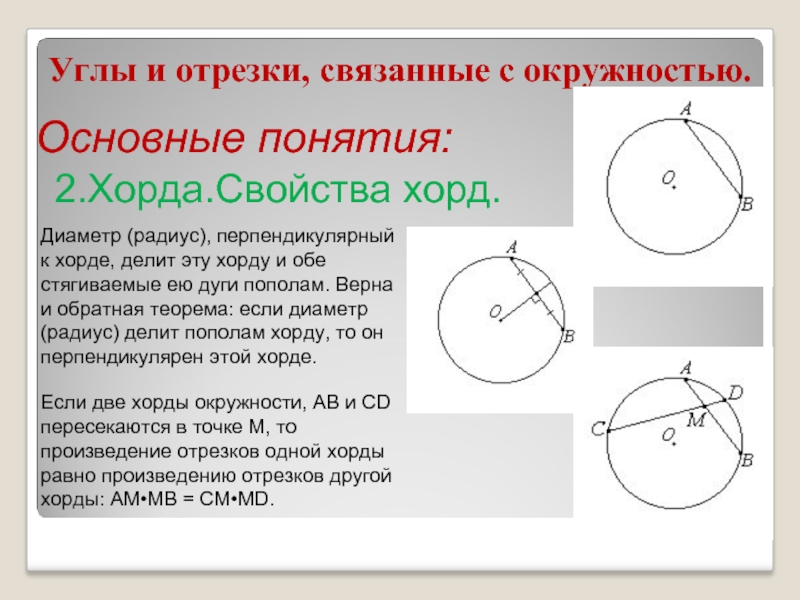
Слайд 5Углы и отрезки, связанные с окружностью.
Основные понятия:
2.Хорда.Свойства хорд.
Диаметр (радиус), перпендикулярный
к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.
Слайд 6Свойства окружности:
Прямая может не иметь с окружностью общих точек; иметь
с окружностью одну общую точку; иметь с ней две общие точки.
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на линии, соединяющей
их центры.
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на линии, соединяющей
их центры.
Слайд 7
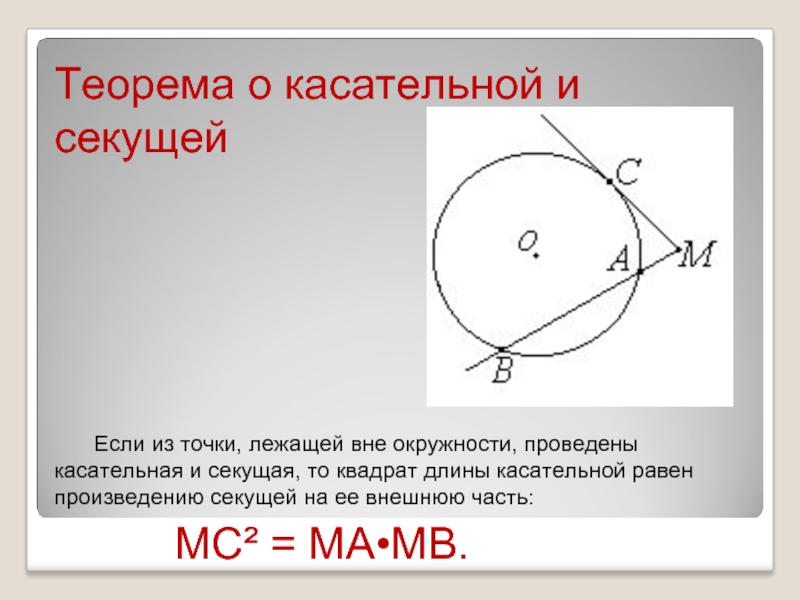
Теорема о касательной и секущей
Если из точки, лежащей вне окружности, проведены
касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть:
MC² = MA•MB.
Слайд 8Теорема о секущих:
Если из точки, лежащей вне окружности, проведены две секущие,
то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть.
MA•MB = MC•MD.
MA•MB = MC•MD.