- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометрия презентация
Содержание
- 1. Тригонометрия
- 2. ЕСЛИ МАТЕМАТИКУ ПОНИМАЕШЬ – ТО
- 3. Давайте ответим на вопросы: Почему в
- 4. Мои выводы: Учиться надо уметь.
- 5. МАТЕМАТИКА – ЭТО ХОРОШАЯ ИГРУШКА.
- 6. Тригонометрия ПОИГРАЕМ В ТРИГОНОМЕТРИЮ или как облегчить себе и ученикам жизнь
- 7. Тригонометрия С В А а c b
- 8. Тригонометрия С В А а c b
- 9. Тригонометрия С В А а c b
- 10. Тригонометрия С В А а c b
- 11. Тригонометрия С В А а c b
- 12. Тригонометрия С В А а c b
- 13. Тригонометрия Как легко запомнить таблицу значений
- 14. Тригонометрия 1 x 9 =
- 15. Тригонометрия 1 x 9 =
- 16. Тригонометрия 1 x 9 =
- 17. Тригонометрия В восьмом классе Незнайка заполнил «–» (минусами) всё, что он не знал
- 18. Тригонометрия 2 2 2 2
- 19. Тригонометрия 2 2 2 2
- 20. Тригонометрия 2 2 2 2
- 21. Тригонометрия 2 2 2 2
- 22. Тригонометрия Таблица готова. А как насчёт
- 23. Тригонометрия Ориентироваться по окружности гораздо проще
- 24. Тригонометрия Неважно в какую четверть мы
- 25. Тригонометрия Рассказ учителя, т.е. живое общение,
- 26. Тригонометрия
Слайд 2ЕСЛИ
МАТЕМАТИКУ ПОНИМАЕШЬ
– ТО ДЕЛАТЬ НЕЧЕГО,
ЕСЛИ НЕ ПОНИМАЕШЬ, ТО
ТОЖЕ
ВЫБИРАЕМ:
КАКОЕ ДЕЛАТЬ НЕЧЕГО
НАМ БОЛЬШЕ НРАВИТСЯ.
Тригонометрия
Слайд 3Давайте ответим на вопросы:
Почему в среднем звене школы некоторые учащиеся неожиданно
Почему у некоторых старательных детей пропадает неожиданно интерес к учебе?
Почему в седьмом классе происходит у одних учащихся улучшение в учебе, а у других наоборот ухудшение?
Тригонометрия
Слайд 4Мои выводы:
Учиться надо уметь.
Учить надо так,
чтобы при минимальных затратах
получать максимальную отдачу.
Для этого можно использовать
ассоциативную память.
Тригонометрия
Слайд 7Тригонометрия
С
В
А
а
c
b
Дан прямоугольный треугольник АВС:
Угол С = 900,
сторона, противолежащая углу С
обозначается с,
сторона, противолежащая углу А
обозначается а,
сторона, противолежащая углу В
обозначается b.
Слайд 8Тригонометрия
С
В
А
а
c
b
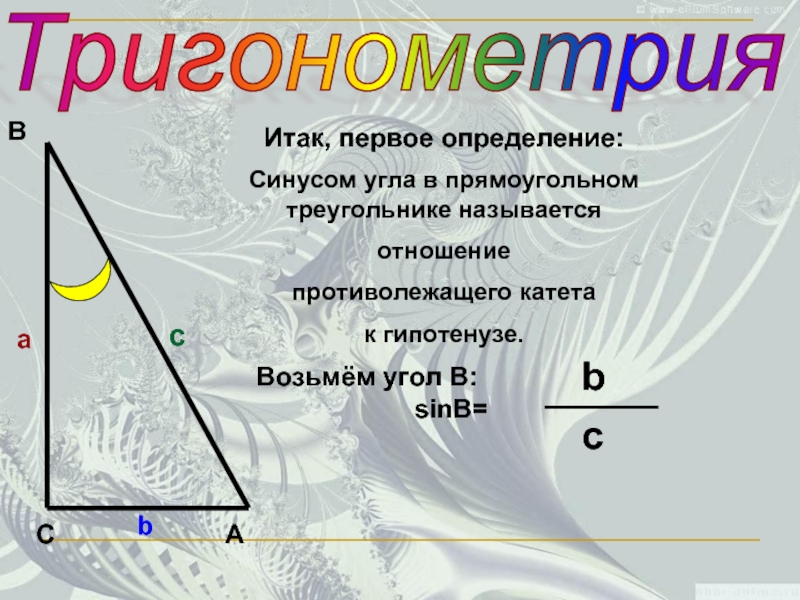
Итак, первое определение:
Синусом угла в прямоугольном треугольнике называется
отношение
противолежащего
к гипотенузе.
Возьмём угол В:
sinB=
b
c
Слайд 9Тригонометрия
С
В
А
а
c
b
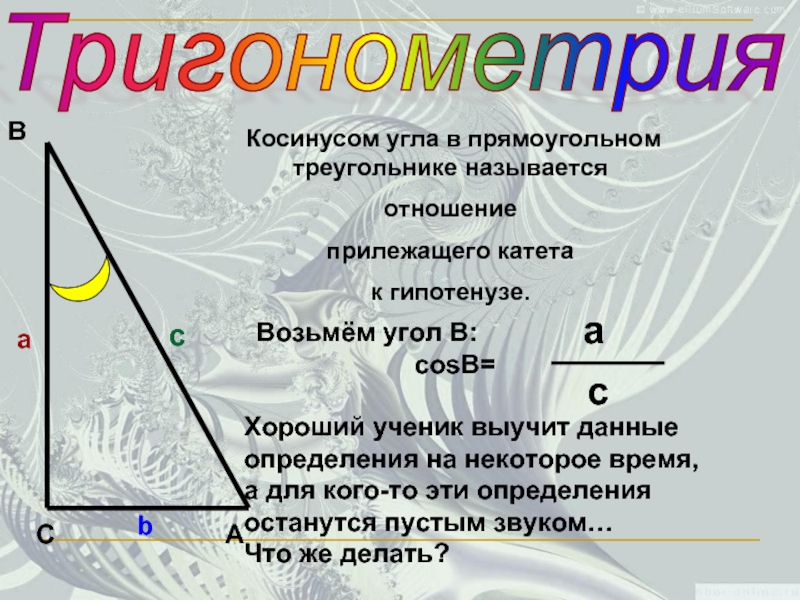
Косинусом угла в прямоугольном треугольнике называется
отношение
прилежащего катета
к гипотенузе.
Возьмём
cosВ=
a
c
Хороший ученик выучит данные определения на некоторое время, а для кого-то эти определения останутся пустым звуком… Что же делать?
Слайд 10Тригонометрия
С
В
А
а
c
b
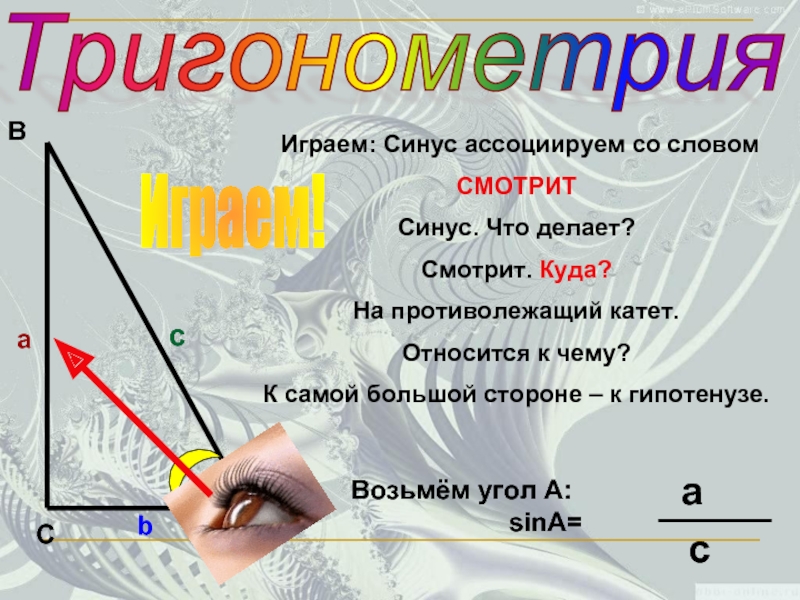
Играем: Синус ассоциируем со словом
СМОТРИТ
Синус. Что делает?
Смотрит. Куда?
На
Относится к чему?
К самой большой стороне – к гипотенузе.
Возьмём угол А:
sinA=
a
c
Играем!
Слайд 11Тригонометрия
С
В
А
а
c
b
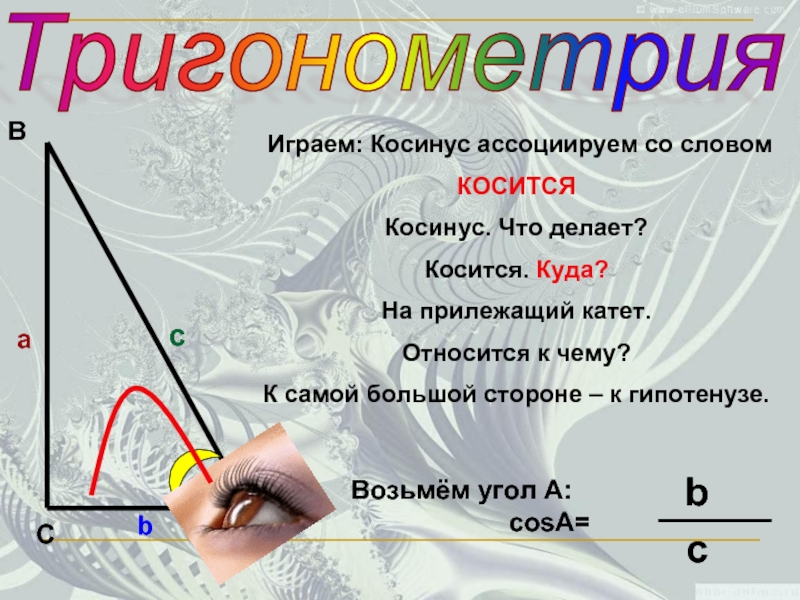
Играем: Косинус ассоциируем со словом
КОСИТСЯ
Косинус. Что делает?
Косится. Куда?
На прилежащий
Относится к чему?
К самой большой стороне – к гипотенузе.
Возьмём угол А:
cosA=
b
c
Слайд 12Тригонометрия
С
В
А
а
c
b
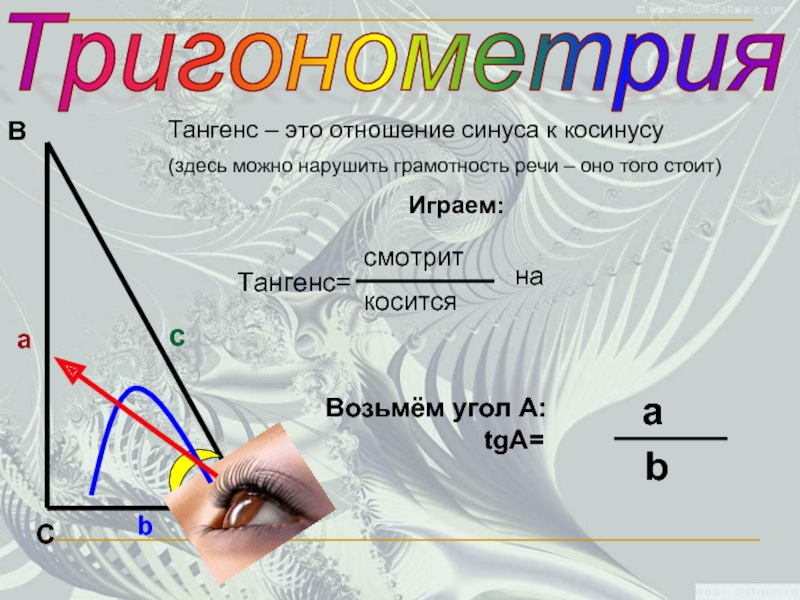
Играем:
Возьмём угол А:
tgA=
a
b
Тангенс
(здесь можно нарушить грамотность речи – оно того стоит)
Тангенс=
смотрит
косится
на
Слайд 13Тригонометрия
Как легко запомнить таблицу значений тригонометрических отношений основных углов в прямоугольном
Для этого надо знать школьный анекдот про Незнайку.
Итак, Незнайке задали во втором классе заполнить ответы к таблице умножения на 9.
Слайд 14Тригонометрия
1 x 9 =
2 x 9 =
3
4 x 9 =
5 x 9 =
6 x 9 =
7 x 9 =
8 x 9 =
9 x 9 =
10 x 9 =
Посмотрел Незнайка на таблицу и сказал:
- Я знаю два ответа: первый и последний…
Слайд 15Тригонометрия
1 x 9 = 9
2 x 9 =
4 x 9 =
5 x 9 =
6 x 9 =
7 x 9 =
8 x 9 =
9 x 9 =
10 x 9 = 90
1 x 9 = 9
2 x 9 = 1
3 x 9 = 2
4 x 9 = 3
5 x 9 = 4
6 x 9 = 5
7 x 9 = 6
8 x 9 = 7
9 x 9 = 8
10 x 9 = 90
Вписал Незнайка свои ответы и решил посчитать сколько же примеров он не знал.
И посчитал…
Слайд 16Тригонометрия
1 x 9 = 9
2 x 9 = 18
4 x 9 = 36
5 x 9 = 45
6 x 9 = 54
7 x 9 = 63
8 x 9 = 72
9 x 9 = 81
10 x 9 = 90
Что-то много я не знаю, - подумал Незнайка и решил пересчитать в обратном порядке
1 x 9 = 9
2 x 9 = 1
3 x 9 = 2
4 x 9 = 3
5 x 9 = 4
6 x 9 = 5
7 x 9 = 6
8 x 9 = 7
9 x 9 = 8
10 x 9 = 90
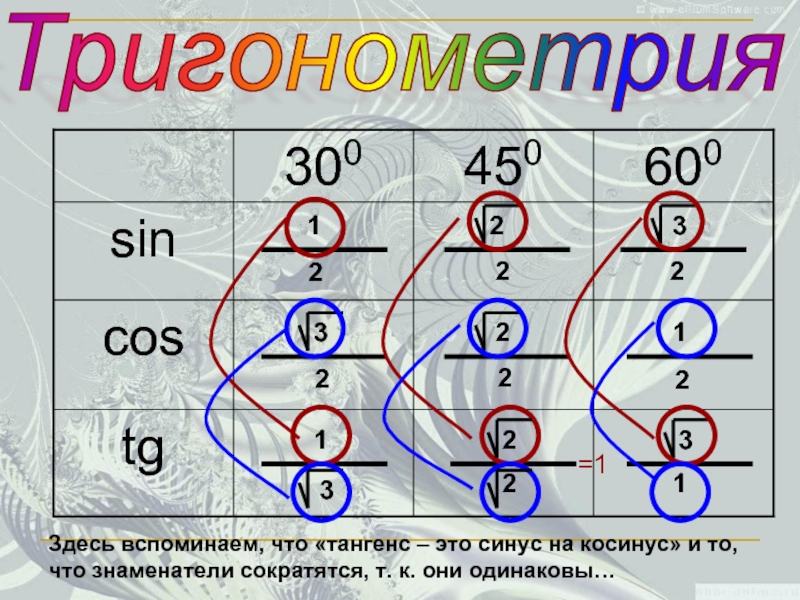
Этот принцип лежит в основе запоминания значений тригонометрических отношений в прямоугольном треугольнике для основных углов
Слайд 19Тригонометрия
2
2
2
2
2
2
2
1
1
2
3
3
Потом посчитал в первой строке в одну сторону, а во второй
Слайд 21Тригонометрия
2
2
2
2
2
2
2
1
1
2
3
3
2
3
3
1
1
2
Здесь вспоминаем, что «тангенс – это синус на косинус» и то,
=1
Слайд 22Тригонометрия
Таблица готова. А как насчёт единичной окружности в тригонометрии? Это же
Спасайся, кто может!
Слайд 23Тригонометрия
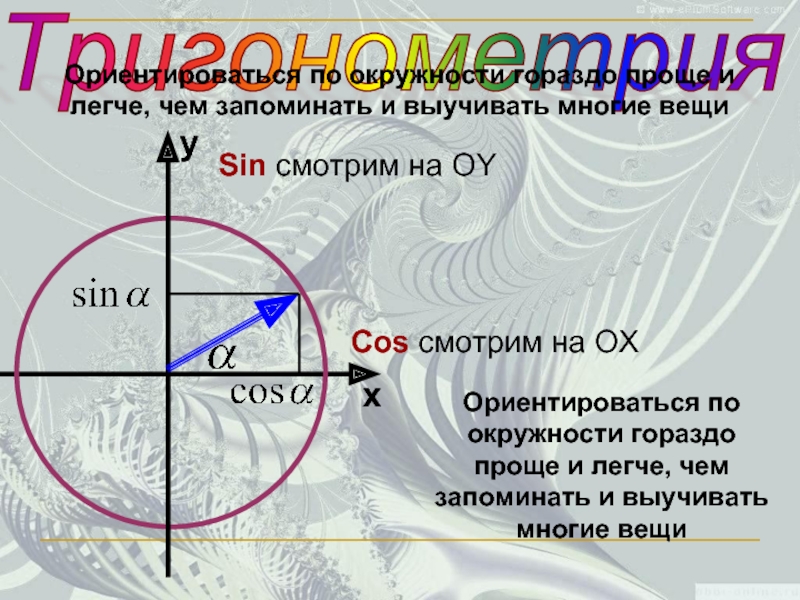
Ориентироваться по окружности гораздо проще и легче, чем запоминать и выучивать
Sin смотрим на OY
Cos смотрим на OX
Ориентироваться по окружности гораздо проще и легче, чем запоминать и выучивать многие вещи
Слайд 24Тригонометрия
Неважно в какую четверть мы попадаем. Самое главное – как мы
Sin смотрим на OY
Cos смотрим на OX
Неважно в какую четверть мы попадаем. Самое главное – как мы срабатываем…
Делаем вывод:
Учиться можно легко и весело.
Слайд 25Тригонометрия
Рассказ учителя, т.е. живое общение, мел и тряпка – незаменимые объекты
Презентация подготовлена к докладу: «Ассоциативные методы развития памяти на примере изучения темы «Тригонометрия»»
Учитель МОУ СОШ №31 г. Иркутска
Максимова Татьяна Вячеславовна
2009 год