- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Треугольники презентация
Содержание
- 1. Треугольники
- 2. Проверим ваши знания: Определение треугольника. Виды треугольников.
- 3. Из истории математики Прямоугольный треугольник
- 4. Треугольники бывают Равносторонние (правильные) Прямоугольные РавнобедренныеРавнобедренные Москва, 2013
- 5. Равносторонние Треугольник, все стороны которого равны, называется
- 6. Прямоугольный треугольник Если один из углов треугольника
- 7. Свойства прямоугольного треугольника Свойство 1 Свойство
- 8. Сумма двух острых углов прямоугольного треугольника
- 9. Катет прямоугольного треугольника , лежащий против угла
- 10. Москва, 2013
- 11. Доказательство: Если катет прямоугольного треугольника равен
- 12. Москва, 2013
- 13. В прямоугольном равнобедренном треугольнике острые углы равны
- 14. Высота прямоугольного треугольника, проведённая
- 15. Катет прямоугольного треугольника есть среднее
- 16. ТЕОРЕМА ПИФАГОРА В прямоугольном треугольнике
- 17. Синус острого угла в прямоугольном треугольнике — это отношение противолежащего
- 18. Признаки равенства прямоугольных треугольников Если катеты одного
- 19. Если катеты одного прямоугольного треугольника соответственно
- 20. Если катет и прилежащий к нему острый
- 21. Если гипотенуза и острый угол одного прямоугольного
- 22. Если гипотенуза и катет одного прямоугольного треугольника
- 23. Равнобедренные Треугольник называется равнобедренным, если у него две
- 24. Пусть Δ ABC – равнобедренный с основанием AB. Рассмотрим Δ BAC . По первому
- 25. Признаки равнобедренного треугольника. Если в треугольнике два
- 26. Пусть Δ ABC – треугольник, в котором A = B. Δ ABC равен Δ BAC по второму признаку
- 27. Задачи по готовым чертежам А С
- 28. Контрольный тест 1. Прямоугольным называется треугольник, у
- 29. 2. В прямоугольном треугольнике всегда
- 30. 3. Стороны прямоугольного треугольника, образующие прямой
- 31. 4. Сторона прямоугольного треугольника, противолежащая прямому углу,
- 32. Контрольный тест Москва, 2013
- 33. Москва, 2013
- 34. Папирус Ахмеса Математический папирус Ахмеса
- 35. Е В К Л И Д Евклид
- 36. Это интересно Треугольник – это многоугольник
- 37. Ответ не правильный. Более внимательно изучи данную тему! Москва, 2013
- 38. Вы верно ответили на все вопросы ! Москва, 2013
- 39. Человек, вооруженный знаниями способен решить любые задачи. Спасибо за урок! Москва, 2013
- 40. Москва, 2013
- 41. Итоговый тест Будьте внимательны Москва, 2013
- 42. Вопрос 1: Выберите верную формулировку определения прямоугольного треугольника: Москва, 2013
- 43. Вопрос 2: Верно ли, что сумма острых
- 44. Вопрос 3: Как называется сторона прямоугольного треугольника,
- 45. Вопрос 4: Как называются стороны прямого угла
- 46. Вопрос 5: Продолжите формулировку: Если острый угол
- 47. Вопрос 6: В треугольнике АВС с прямым
- 48. Вопрос 7: На рисунке изображен треугольник АВС,
- 49. Вопрос 8: Каким свойством обладает катет прямоугольного
- 50. Москва, 2013
- 51. С В А 4
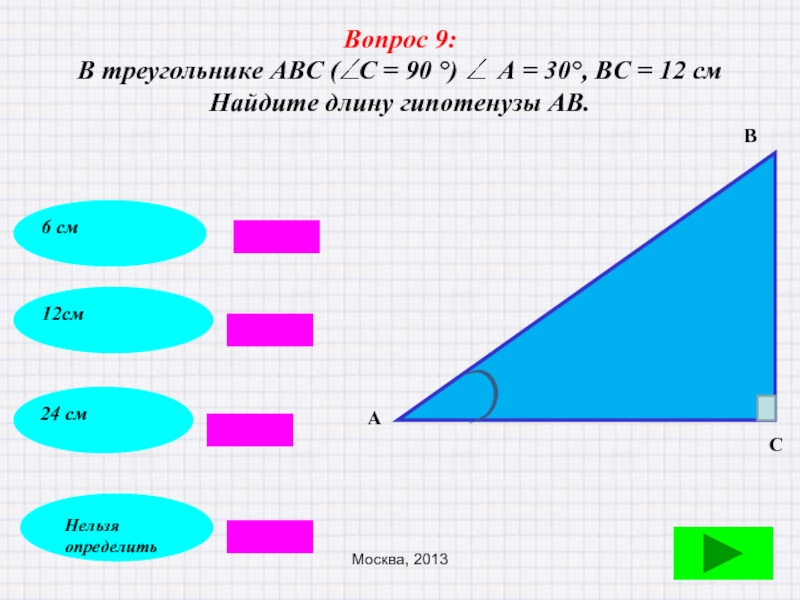
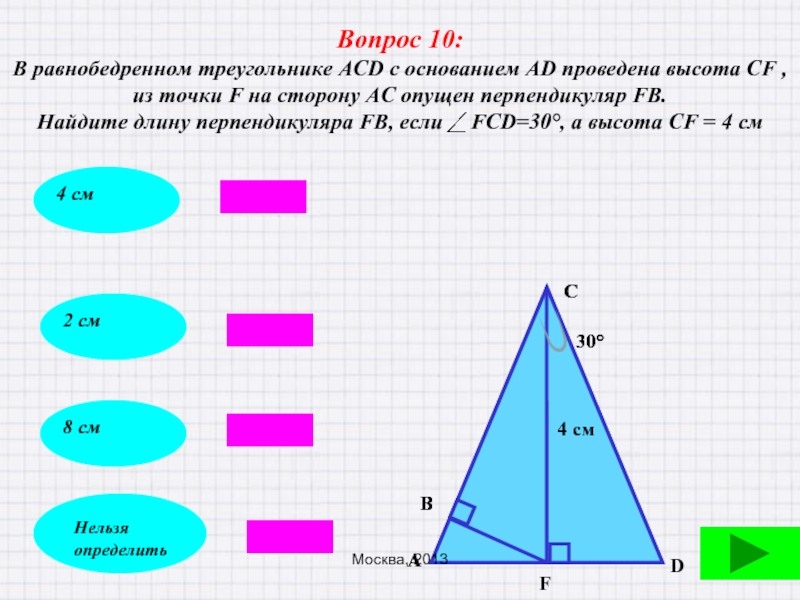
- 52. Вопрос 11: В равнобедренном треугольнике АВС с
- 53. Вопрос 12: В равнобедренном треугольнике АВС с
- 54. Вопрос 13: В прямоугольном равнобедренном треугольнике гипотенуза
- 55. На ошибках учатся! Повтори теорию еще раз
- 56. Ты хорошо поработал! Приступай к решению следующей задачи. МОЛОДЕЦ Москва, 2013
Слайд 2Проверим ваши знания:
Определение треугольника.
Виды треугольников.
3) Свойства прямоугольного треугольника.
4) Свойства равнобедренного треугольника.
5)Теорема
6)Теорема косинусов.
Москва, 2013
Слайд 3Из истории математики
Прямоугольный треугольник занимает почётное место в вавилонской
геометрии, упоминание о нём часто встречается в папирусе Ахмеса.
Термин гипотенуза происходит от греческого hypoteinsa,
означающего тянущаяся под чем либо , стягивающая.
Слово берёт начало от образа древнеегипетских арф, на которых струны
натягивались на концы двух взаимно перпендикулярных подставок.
Термин катет происходит от греческого слова «катетос »,
которое означало отвес , перпендикуляр. В средние века словом катет
означали высоту прямоугольного треугольника, в то время, как другие его
стороны называли гипотенузой, соответственно основанием.
В XVII веке слово катет начинает применяться в современном смысле и
широко распространяется, начиная с XVIII века.
Евклид употребляет выражения:
«стороны, заключающие прямой угол», - для катетов;
«сторона, стягивающая прямой угол», - для гипотенузы.
Москва, 2013
Слайд 4Треугольники бывают
Равносторонние (правильные)
Прямоугольные
РавнобедренныеРавнобедренные
Москва, 2013
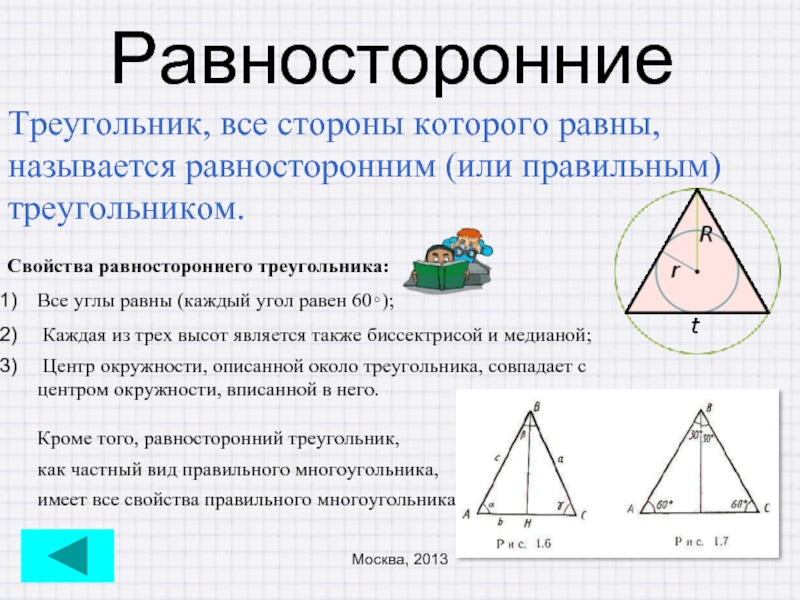
Слайд 5Равносторонние
Треугольник, все стороны которого равны, называется равносторонним (или правильным) треугольником.
Свойства равностороннего
Все углы равны (каждый угол равен 60∘);
Каждая из трех высот является также биссектрисой и медианой;
Центр окружности, описанной около треугольника, совпадает с центром окружности, вписанной в него. Кроме того, равносторонний треугольник,
как частный вид правильного многоугольника,
имеет все свойства правильного многоугольника.
Москва, 2013
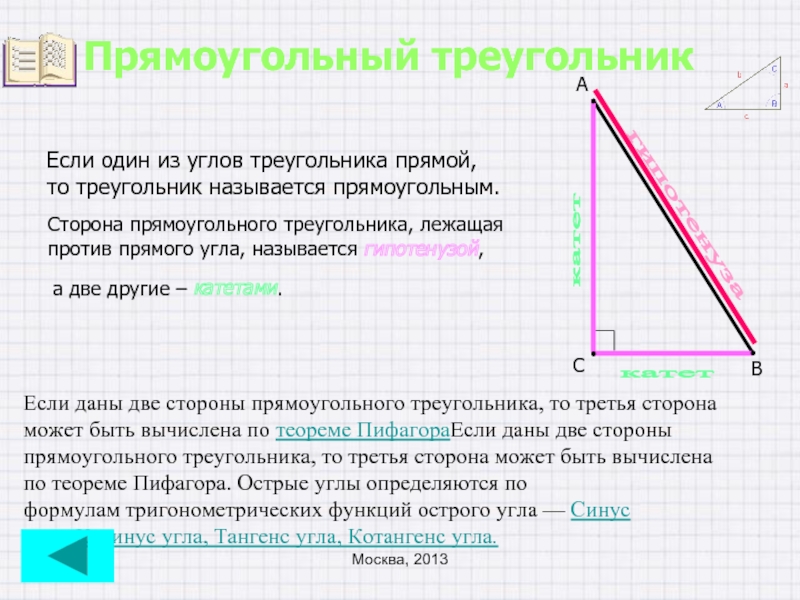
Слайд 6Прямоугольный треугольник
Если один из углов треугольника прямой,
то треугольник называется прямоугольным.
А
В
С
Сторона
против прямого угла, называется гипотенузой,
гипотенуза
катет
катет
а две другие – катетами.
Если даны две стороны прямоугольного треугольника, то третья сторона может быть вычислена по теореме ПифагораЕсли даны две стороны прямоугольного треугольника, то третья сторона может быть вычислена по теореме Пифагора. Острые углы определяются по формулам тригонометрических функций острого угла — Синус угла, Косинус угла, Тангенс угла, Котангенс угла.
Москва, 2013
Слайд 8
Сумма двух острых углов прямоугольного треугольника равна 90°
Доказательство:
Сумма углов треугольника равна
Свойство 1
∠С=90°
∠А+∠В=90°
Москва, 2013
Слайд 9Катет прямоугольного треугольника , лежащий против угла в 30°, равен половине
Доказательство:
Приложим к треугольнику АВС равный ему треугольник АВД.
Свойство 2
Москва, 2013
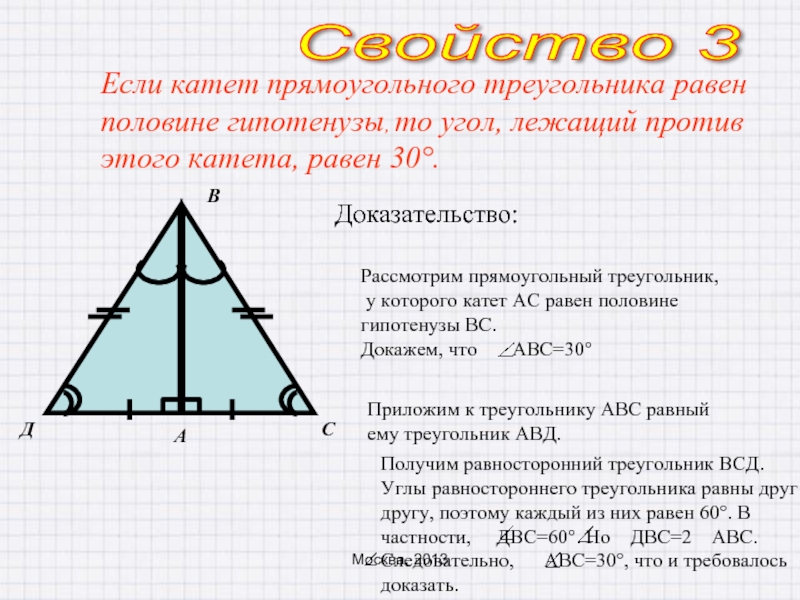
Слайд 11
Доказательство:
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против
Приложим к треугольнику АВС равный ему треугольник АВД.
Свойство 3
Москва, 2013
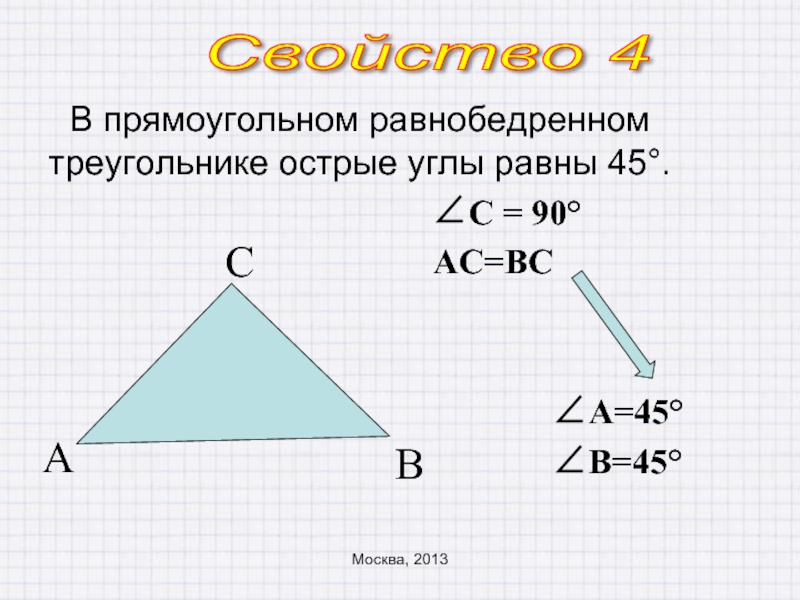
Слайд 13В прямоугольном равнобедренном треугольнике острые углы равны 45°.
∠С = 90°
АС=ВС
∠А=45°
∠В=45°
А
В
С
Свойство 4
Москва, 2013
Слайд 14
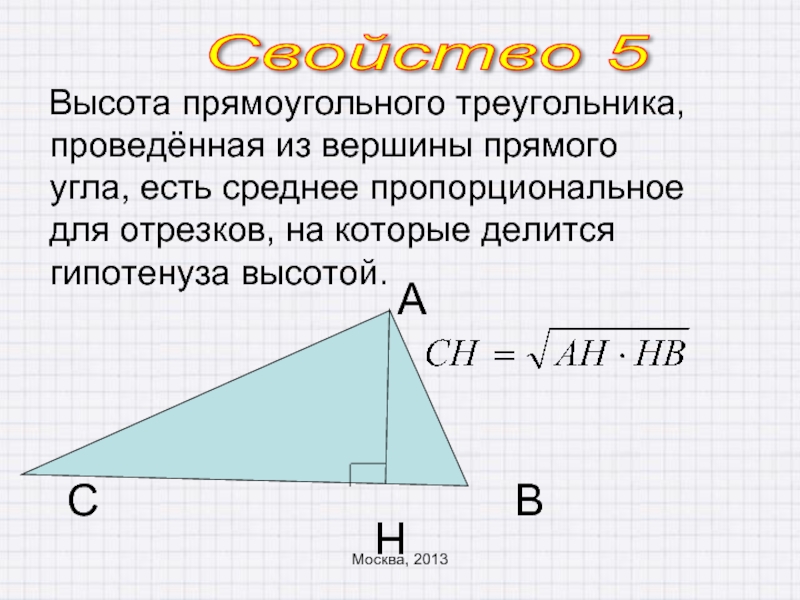
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть
С
А
Н
В
Свойство 5
Москва, 2013
Слайд 15 Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и
С
А
Н
В
Свойство 6
Москва, 2013
Слайд 16ТЕОРЕМА ПИФАГОРА
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
Москва, 2013
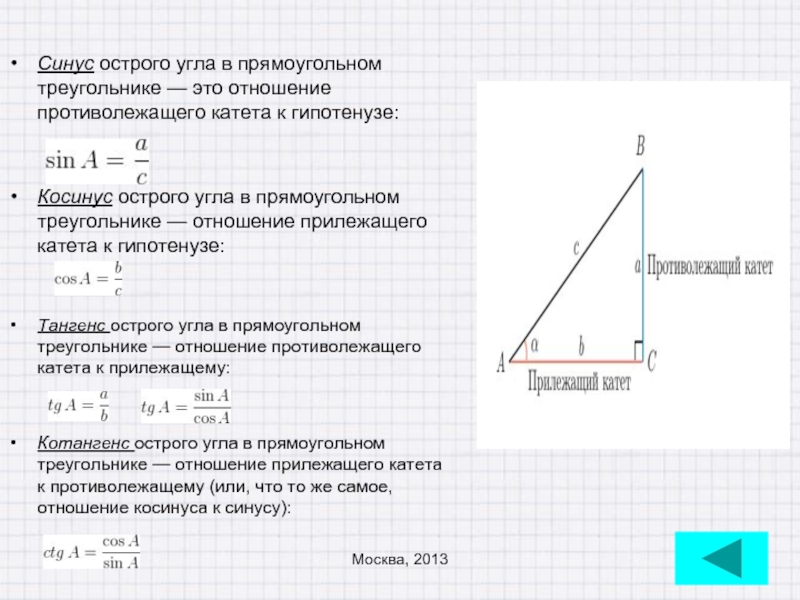
Слайд 17Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Москва, 2013
Слайд 18Признаки равенства
прямоугольных треугольников
Если катеты одного прямоугольного треугольника
соответственно равны катетам другого,
2. Если катет и прилежащий к нему острый угол одного прямоугольного
треугольника соответственно равны катету и прилежащему к нему углу
другого, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника
соответственно равны гипотенузе и острому углу другого,
то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника
соответственно равны гипотенузе и катету другого,
то такие треугольники равны.
Москва, 2013
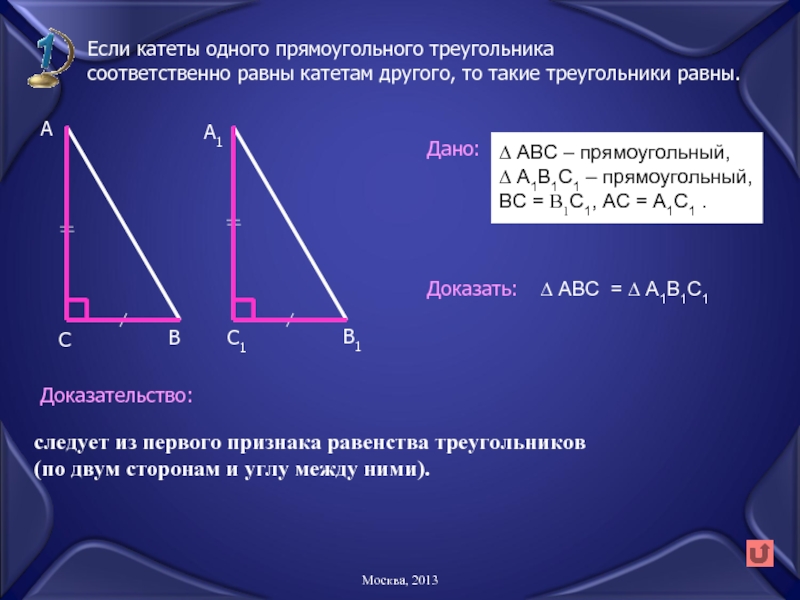
Слайд 19Если катеты одного прямоугольного треугольника
соответственно равны катетам другого, то такие
Дано:
Доказать:
Доказательство:
В
А
А1
С
С1
В1
∆ АВС = ∆ А1В1С1
следует из первого признака равенства треугольников
(по двум сторонам и углу между ними).
Москва, 2013
Слайд 20Если катет и прилежащий к нему острый угол одного прямоугольного
треугольника
другого, то такие треугольники равны.
В
А
А1
С
С1
В1
Дано:
Доказать:
Доказательство:
следует из второго признака равенства треугольников
(по стороне и прилежащим к ней углам)
∆ АВС = ∆ А1В1С1
Москва, 2013
Слайд 21Если гипотенуза и острый угол одного прямоугольного треугольника
соответственно равны гипотенузе
то такие треугольники равны.
В
А
А1
С
С1
В1
Дано:
Доказать:
Доказательство:
т.к. сумма острых углов прямоугольного треугольника равна 90°,
то два других острых угла также равны,
∆ АВС = ∆ А1В1С1
Москва, 2013
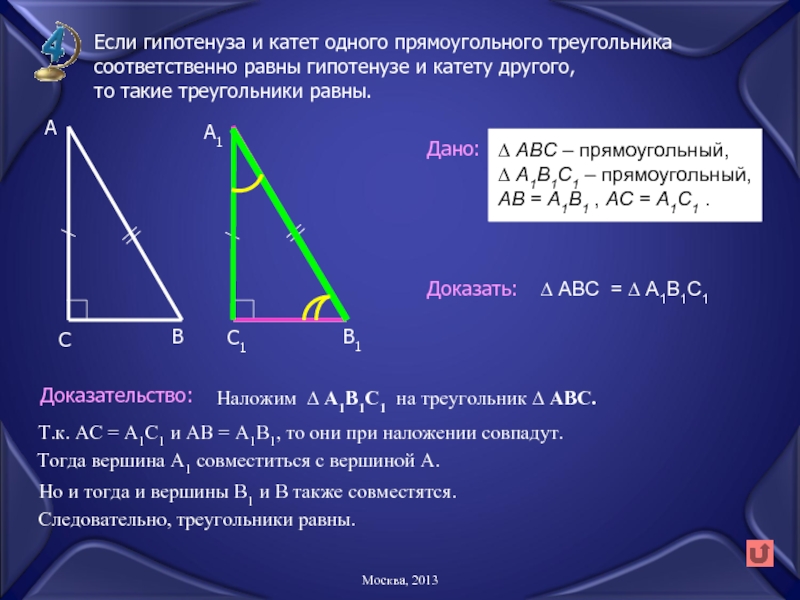
Слайд 22Если гипотенуза и катет одного прямоугольного треугольника
соответственно равны гипотенузе и
то такие треугольники равны.
В
А
А1
С
С1
В1
Дано:
Доказать:
Доказательство:
∆ АВС = ∆ А1В1С1
Наложим ∆ А1В1С1 на треугольник ∆ АВС.
Т.к. АС = А1С1 и АВ = А1В1, то они при наложении совпадут.
Тогда вершина А1 совместиться с вершиной А.
Но и тогда и вершины В1 и В также совместятся.
Следовательно, треугольники равны.
Москва, 2013
Слайд 23Равнобедренные
Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны называются боковыми,
В равнобедренном треугольнике углы при основании равны. (Доказательство)
Свойство медианы равнобедренного треугольника.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. (Доказательство )
Москва, 2013
Слайд 24Пусть Δ ABC – равнобедренный с основанием AB. Рассмотрим Δ BAC . По первому признаку эти треугольники равны.
Пусть Δ ABC – равнобедренный с основанием AB, и CD – медиана, проведенная к основанию. В треугольниках CAD и CBD углы CAD и CBD равны, как углы при основании равнобедренного треугольника (по теореме 4.3), стороны AC и BC равны по определению равнобедренного треугольника, стороны AD и BD равны, потому что D – середина отрезка AB. Отсюда получаем, что Δ ACD = Δ BCD.
Из равенства треугольников следует равенство соответствующих углов: ACD = BCD, ADC = BDC. Из первого равенства следует, что CD – биссектриса. Углы ADC и BDC смежные, и в силу второго равенства они прямые, поэтому CD – высота треугольника. Теорема доказана.
Москва, 2013
Слайд 25Признаки равнобедренного треугольника.
Если в треугольнике два угла равны, то он равнобедренный.
Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
(Доказательство)
Москва, 2013
Слайд 26
Пусть Δ ABC – треугольник, в котором A = B. Δ ABC равен Δ BAC по второму признаку равенства треугольников. Действительно: AB = BA; B = A; A = B. Из равенства
В треугольнике ABC проведем медиану BD, которая по условию также является высотой. Прямоугольные треугольники ABD и CBD равны, т. к. катет BD общий,AD = CD по построению. Следовательно, гипотенузы этих треугольников равны как соответственные элементы равных треугольников, т. е. AB = BC. Теорема доказана.
Москва, 2013
Слайд 27Задачи по готовым чертежам
А
С
В
D
?
В
А
С
370
?
?
А
В
С
700
?
А
В
С
300
15 см
?
1200
4 см
D
С
А
В
?
4,2 см
8,4 см
Москва, 2013
Слайд 28Контрольный тест
1. Прямоугольным называется треугольник, у которого
б) два угла прямые;
в) один прямой угол.
Москва, 2013
Слайд 292. В прямоугольном треугольнике всегда
а) два угла острых и
б) один острый угол, один прямой и один тупой угол;
в) все углы прямые.
Контрольный тест
Москва, 2013
Слайд 303. Стороны прямоугольного треугольника, образующие
прямой угол, называются
б) катетами треугольника;
в) гипотенузами треугольника.
Контрольный тест
Москва, 2013
Слайд 314. Сторона прямоугольного треугольника, противолежащая прямому углу, называется
б) катетом треугольника;
в) гипотенузой треугольника.
Контрольный тест
Москва, 2013
Слайд 34Папирус Ахмеса
Математический папирус Ахмеса — древнеегипетское учебное руководство по
Папирус Ахмеса был обнаружен в 1858 шотландским египтологом Генри Риндом и часто называется папирусом Райнда по имени его первого владельца. В 1870 папирус был расшифрован, переведён и издан. Ныне большая часть рукописи находится в Британском музеев Лондоне, а вторая часть — в Нью - Йорке.
Этот документ остается основным источником информации по математике древнего Египта. Он содержит чертежи треугольников с указаниями углов и формулами нахождения площадей.
Во вступительной части папируса Райнда объясняется, что он посвящён «совершенному и основательному исследованию всех вещей, пониманию их сущности, познанию их тайн». Все задачи, приведённые в тексте, имеют в той или другой степени практический характер и могли быть применены в строительстве, размежевании земельных наделов и других сферах жизни и производства. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами, пропорциональное деление, нахождение отношений.
Москва, 2013
Слайд 35Е В К Л И Д
Евклид (Eνκλειδηζ), древнегреческий математик, автор первого
Сведения об Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в III веке до н. э. Евклид – первый математик александрийской школы. Его главная работа «Начала»
(в латинизированной форме – «Элементы») содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел; в ней он подвел итог предшествующему развитию греческой математики и создал фундамент дальнейшего развития математики.
Из других сочинений по математике надо отметить работу «О делении фигур», сохранившуюся в арабском переводе, четыре книги «Конические сечения», материал которых вошел в произведение того же названия Аполлония Пергского, а также «Поризмы», представление о которых можно получить из «Математического собрания» Паппа Александрийского. Евклид – автор работ по астрономии, оптике, музыке и др.
Дошедшие до нас произведения Евклида собраны в издании «Euclidis opera omnia», ed. J. L. Heibert et Н. Menge, v. 1–9, 1883–1916, дающем их греческие подлинники, латинские переводы и комментарии позднейших авторов.
Москва, 2013
Слайд 36
Это интересно
Треугольник – это многоугольник с тремя сторонами (или тремя углами).
Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.
В любом треугольнике:
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
3. Сумма углов треугольника равна 180 º
4. Продолжая одну из сторон треугольника, получаем внешний угол.
Внешний угол треугольника равен сумме внутренних углов, не смежных с ним.
5. Любая сторона треугольника меньше суммы двух других сторон и
больше их разности ( a < b + c, a > b – c; b < a + c, b > a – c; c < a + b, c > a – b ).
Москва, 2013
Слайд 43Вопрос 2: Верно ли, что сумма острых углов прямоугольного треугольника равна
180°
Москва, 2013
Слайд 44Вопрос 3: Как называется сторона прямоугольного треугольника, противолежащая прямому углу?
Москва, 2013
Слайд 46Вопрос 5: Продолжите формулировку:
Если острый угол прямоугольного треугольника равен 30°, то…
Москва,
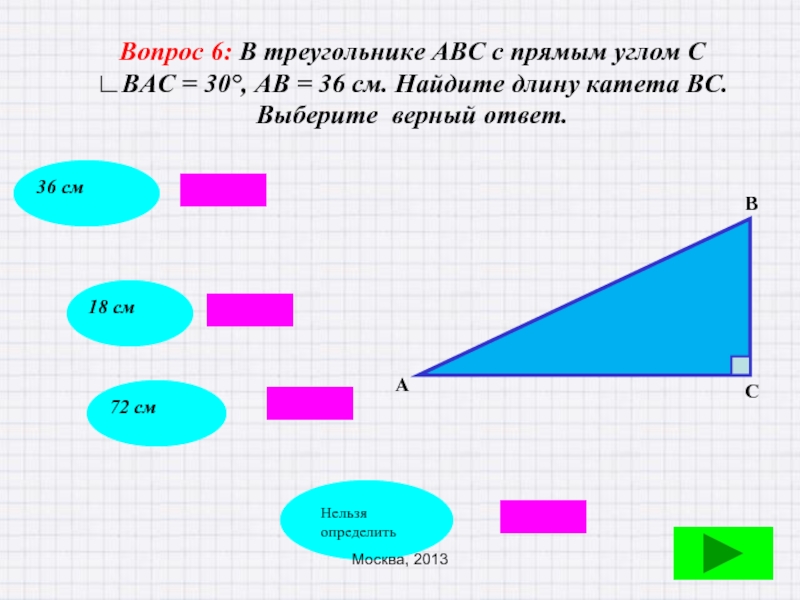
Слайд 47Вопрос 6: В треугольнике АВС с прямым углом С ∟ВАС =
Выберите верный ответ.
В
С
А
Москва, 2013
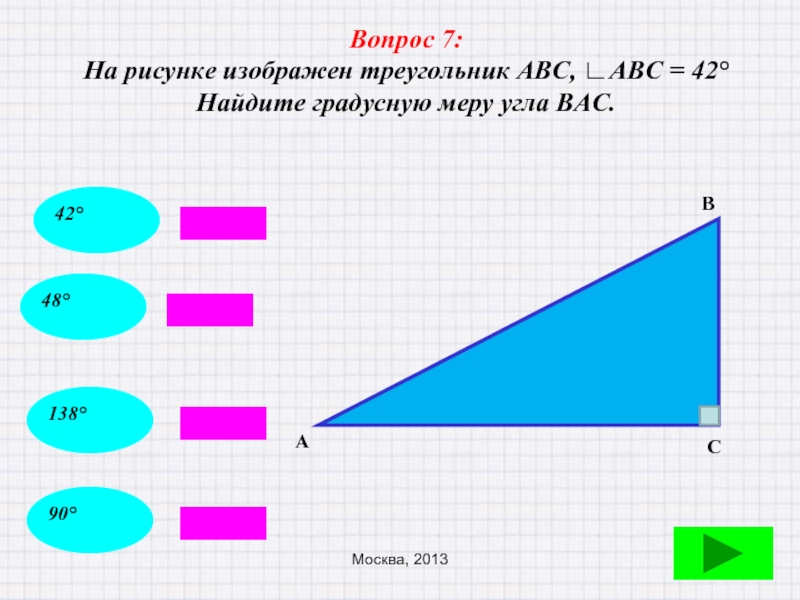
Слайд 48Вопрос 7:
На рисунке изображен треугольник АВС, ∟АВС = 42°
Найдите градусную меру
В
А
С
Москва, 2013
Слайд 49Вопрос 8: Каким свойством обладает катет прямоугольного треугольника, противолежащий углу в
Москва, 2013
Слайд 52Вопрос 11: В равнобедренном треугольнике АВС с основанием ВС проведена высота
Найдите величины углов В и С, если
боковая сторона треугольника АС=7 см, а СD=3,5 см
Москва, 2013
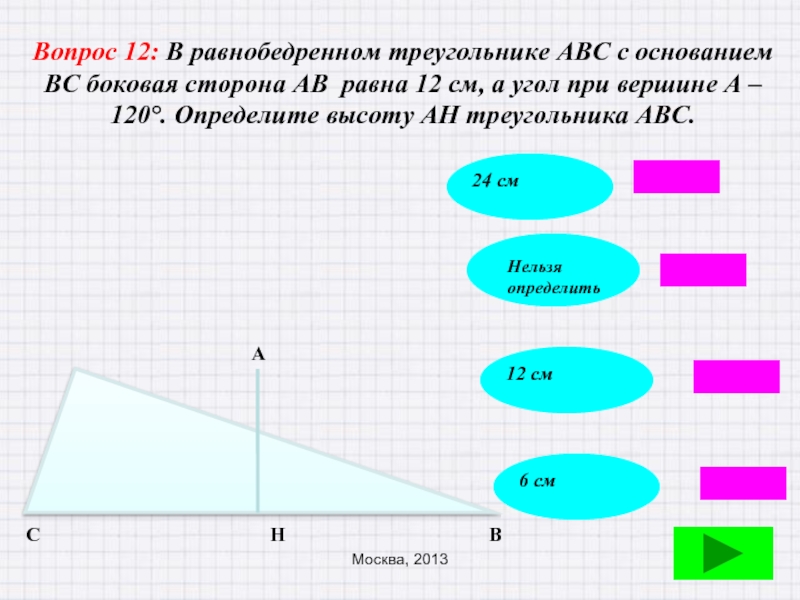
Слайд 53Вопрос 12: В равнобедренном треугольнике АВС с основанием ВС боковая сторона
А
С
Н
В
Москва, 2013
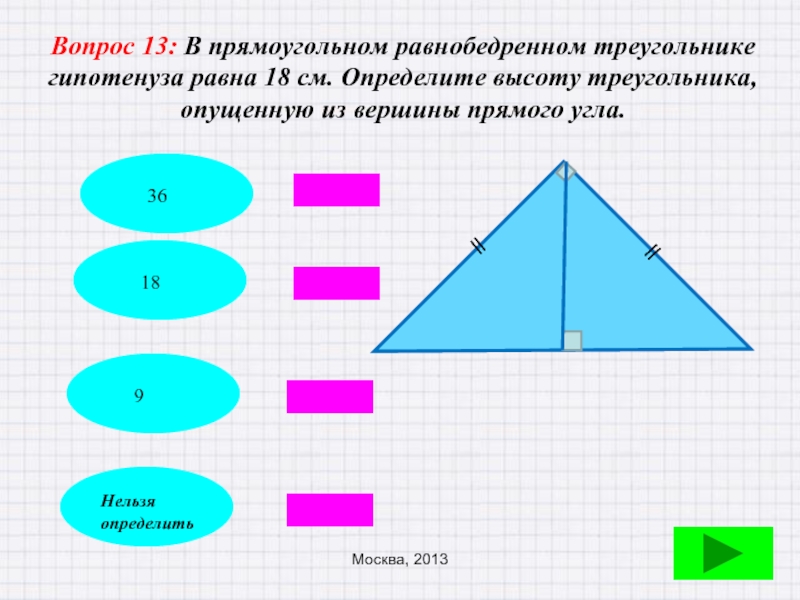
Слайд 54Вопрос 13: В прямоугольном равнобедренном треугольнике гипотенуза равна 18 см. Определите
=
=
Москва, 2013