- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
The homology groups of a partial monoid action category презентация
Содержание
- 1. The homology groups of a partial monoid action category
- 2. Partial monoid action on a set Denote
- 3. A category for a monoid partial
- 4. Trace monoids Let E be a set
- 5. Examples of trace monoids E ={a,b}, I
- 6. Interpretation of traces Any trace w ∈
- 7. Classifying space Let C be a small
- 8. Purpose of the report The studying Baues-Wirsching
- 9. Homology of categories Let C be a
- 10. Category of factorizations Let C be a
- 11. Baues-Wirsching homology Let C be a small
- 12. Baues-Wirsching homology Let S be a
- 13. Homology of classifying space for the
- 14. Homology of the classifying space for
- 15. Computing the homology groups Let k be
- 16. Example for Corollary 1 Example 3.
- 17. Directed homology groups Let Δ0Z: K(S)→Ab and
- 18. Directed homology groups Corollary 2. In the
- 19. Example of computing the directed homology groups
- 20. Example of computing the directed homology groups
- 21. Interpretation of homology groups H00 and H01
- 22. Local homology Consider decompositions
- 23. Computing the local homology groups where Differentials
- 24. Computing the local homology groups Hn0
- 25. Example 5. number of the final
- 26. Computing the local homology groups Hn1 where
- 27. Computing the local groups Hn1 number
- 28. Connection with bisimulation equivalence Corollary 4. For
- 29. Connection with bisimulation equivalence Proposition 5. A
- 30. Connection with bisimulation equivalence Theorem. If pointed
- 31. Example of trace equivalent asynchronous systems which
- 32. Perspectives Studying the homotopical colimits of diagrams
Слайд 1The homology groups
of a partial monoid action category
Ahmet A. Husainov
husainovhusainov51husainov51@yandex.ru
http://husainov51.narod.ru/en
Слайд 2Partial monoid action on a set
Denote by PSet the category of
Let M be a monoid and let S be a set.
Partial right action of M on S is a homomorphism of monoids Mop → PSet(S,S)
Example 1.
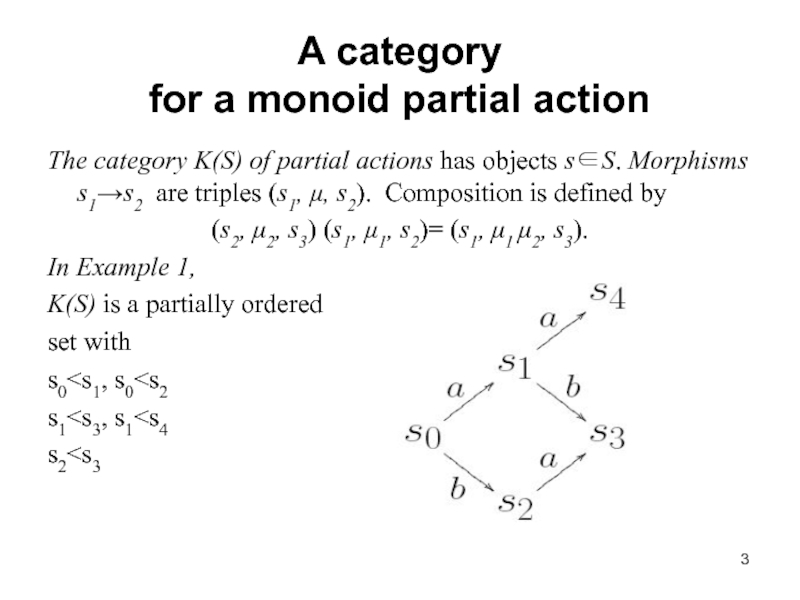
M=N2 ={apbq : p, q=0, 1, 2, …},
S= {s0, s1, s2, s3, s4}
s0a=s1, s0b=s2
s1a=s4, s1b=s3
s2a=s3
Слайд 3A category
for a monoid partial action
The category K(S) of partial
(s2, μ2, s3) (s1, μ1, s2)= (s1, μ1 μ2, s3).
In Example 1,
K(S) is a partially ordered
set with
s0
Слайд 4Trace monoids
Let E be a set and let I ⊆ E×E
Free partially commutative monoid (or trace monoid) M(E,I) is a quotient monoid E*/(≡) where E* is a monoid of all words in alphabet E and (≡) is smallest equivalence relation for which
uabv ≡ ubav, for all (a,b)∈I, u∈ E*, v∈ E*
Trace monoid M(E,I) is called to be locally finite dimensional if E does not contain infinite subsets of pairwise independent elements
Слайд 5Examples of trace monoids
E ={a,b}, I ={(a,b),(b,a)},
M(E,I) ≅ N2 is
E ={a,b}, I = ∅,
M(E,I) ≅ {a,b}* is a free monoid
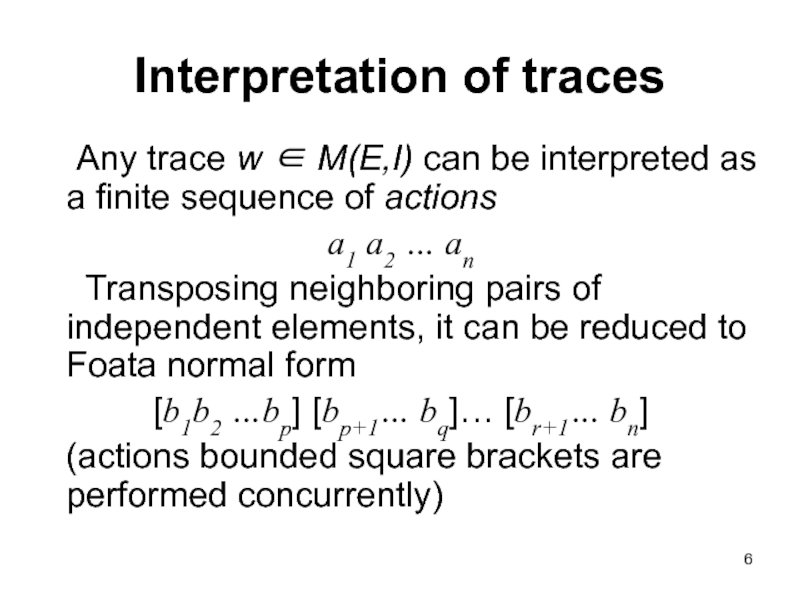
Слайд 6Interpretation of traces
Any trace w ∈ M(E,I) can be interpreted as
a1 a2 … an
Transposing neighboring pairs of independent elements, it can be reduced to Foata normal form
[b1b2 …bp] [bp+1… bq]… [br+1… bn]
(actions bounded square brackets are performed concurrently)
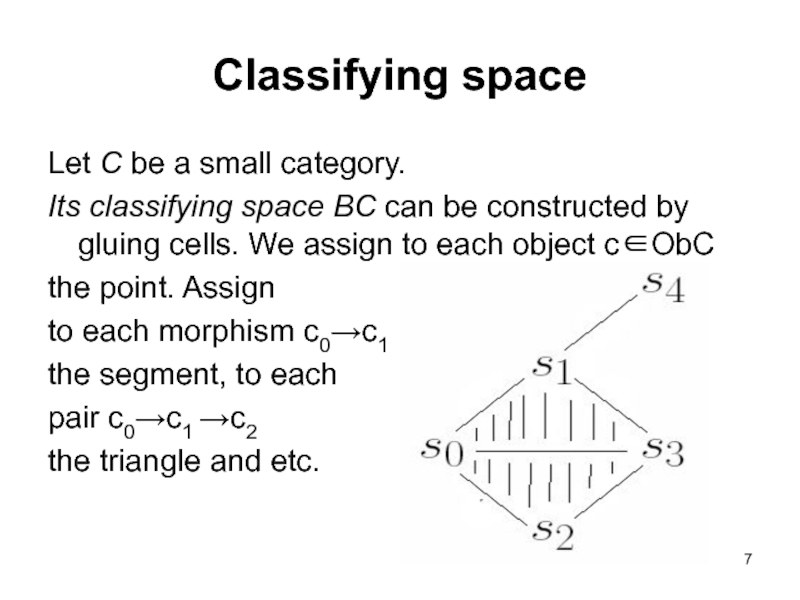
Слайд 7Classifying space
Let C be a small category.
Its classifying space BC
the point. Assign
to each morphism c0→с1
the segment, to each
pair c0→с1 →с2
the triangle and etc.
Слайд 8Purpose of the report
The studying Baues-Wirsching homology groups of the category
Application of the Baues-Wirsching homology for building the algorithms for computing the homology groups of the space B(K (S)) and directed homology groups for a partial trace monoid action.
Слайд 9Homology of categories
Let C be a small category and let
colimC: AbC
0 ←F ← P0 ← P1 ← … ← Pn ← Pn+1 ← …
and a complex С* of Abelian groups
0 ← colimC P0 ← colimC P1 ← …
…← colimC Pn ← colimC Pn+1 ← …
The groups Hn(C,F)≅Hn(С*), n≥0, are called
homology groups of the category C
with coefficients in F.
Слайд 10Category of factorizations
Let C be a small category. Objects of a
in Fact(C) are given by commutative diagrams
Example 2. Let M be a monoid considered as the category. Then Ob(Fact (M) )= M. Its morphisms from α to β are pairs (f,g) of f, g ∈ M for which gαf=β.
Proposition 1. Fact(C)≅Fact(Cop)
Слайд 11Baues-Wirsching homology
Let C be a small category.
For any functor F:
Hn(Fact(C)op,F) are called Baues-Wirsching homology groups of C with coefficients in contravariant natural systems F on C.
If C=M is a monoid, then Hn(Fact(M)op,F) are Leech homology groups of a diagram F
Слайд 12Baues-Wirsching homology
Let S be a set with partial action of
Let K(S) be the action category with morphisms
Consider a functor F: Fact(K(S))op →Ab and the functor
U: K(S) →Mop defined as U(s1,μ,s2)= μ.
Theorem. Hn(Fact(K(S))op,F)≅ Hn(Fact(M)op,L(F))
Here L(F) is a left Kan extension of the functor F along the functor
Fact(K(S))op→Fact(M)op,
determined by the functor U.
Слайд 13Homology of classifying space
for the action category
Let M(E,I) be a
For n= 0, 1, 2, … , introduce sets
Tn(E,I)={(a1,…, an)| ai
In particular, T0(E,I)={1}.
For an arbitrary set S, denote by LS a free Abelian group generated by S.
Слайд 14Homology of the classifying space
for the action category
A polygon S
Corollary 1. Let S be a polygon over a locally finite dimensional trace monoid M(E,I). Groups Hn(B(K(S))) isomorphic to homology groups of complex
Here sμ ∈S denotes that sμ is defined.
Слайд 15Computing the homology groups
Let k be a field and let
be a
Hn=Ker dn / Im dn+1 = kdimCn-r(dn)-r(dn+1) where r(A) is denoted the rank of matrix A
Proposition 2. Let A be a matrix with integer entries. Then there are matrixes S, T, D, for which
A= T°D°S 2) |det S|=|det T|=1
3) D is a diagonal matrix
with δ1 | δ2 | … | δr
D is Smith normal form of A
If k=Z is a ring of integers, then the homology groups can be computing by the Smith normal form:
Hn=Ker dn / Im dn+1 = ZdimCn-r(dn)-r(dn+1)×Z/δ1Z×…× Z/ δr Z , r=r(dn+1)
Слайд 16Example for Corollary 1
Example 3.
C0=L{s0,s1}, C1=L{(s0,a), (s0,b), (s1,a)},
C2=L{(s0,a,b)}
We obtain H0=Z2-1=Z,
Слайд 17Directed homology groups
Let Δ0Z: K(S)→Ab and Δ1Z: K(S)op→Ab be functors with
Groups Hn0(S,M(E,I)) =def Hn(K(S), Δ0Z)
and Hn1(S,M(E,I)) =опр Hn(K(S)op, Δ1Z) are called
directed homology groups.
Слайд 18Directed homology groups
Corollary 2. In the conditions of Corollary 1 the
Hn1(S,M(E,I)) can be computed by a similar complex with differentials
Слайд 19Example of computing the directed homology groups
Example 4.
Groups H00 and
C0=L{s0,s1,s2 }, C1=L{(s0,a), (s0,b)},
We obtain H00=Z3-1=Z2, H10=Z2-1 = Z .
Слайд 20Example of computing the directed homology groups
Groups H01 and H11
C0=L{s0,s1,s2 },
Obtain H00=Z3-2=Z, H10=Z2-2 = 0.
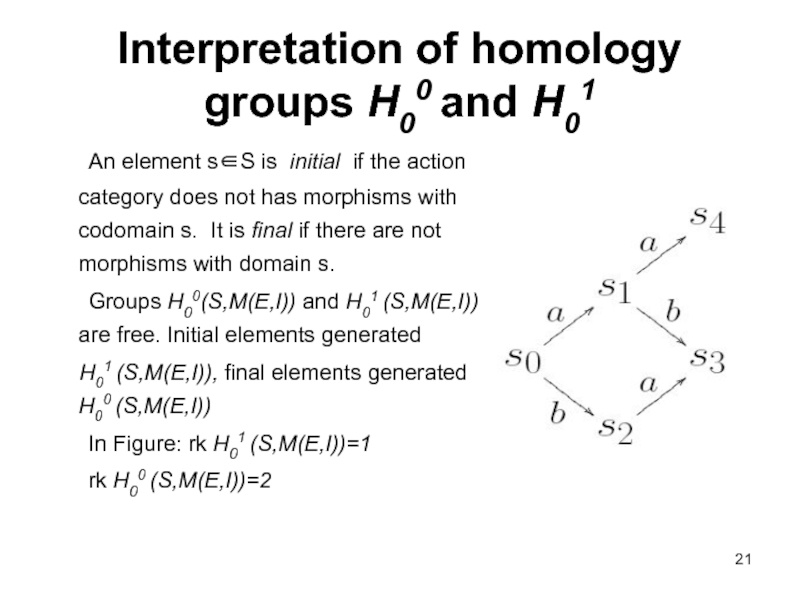
Слайд 21Interpretation of homology groups H00 and H01
An element s∈S is initial
Groups H00(S,M(E,I)) and H01 (S,M(E,I)) are free. Initial elements generated
H01 (S,M(E,I)), final elements generated H00 (S,M(E,I))
In Figure: rk H01 (S,M(E,I))=1
rk H00 (S,M(E,I))=2
Слайд 22Local homology
Consider decompositions
where is a functor defined as
Similarly defined the functor .
We obtain decomposition the directed homology groups. Local homology groups of the category for the partial trace monoid action M(E,I) on S are defined as
Слайд 23Computing the local homology groups
where
Differentials are defined as
Proposition 3. Let
can be computed by the following complex
Слайд 24Computing the local homology groups Hn0
Corollary 3.
Let S
Its sets of n-simplexes equal
Recall that
Слайд 26Computing the local homology groups Hn1
where
Differentials are defined as
Proposition 4.
Слайд 28Connection with bisimulation equivalence
Corollary 4. For s∈S, consider the complex
Let S be a polygon over M(E,I). For s∈S, we can remove the condition e1<… There are isomorphisms
Слайд 29Connection with bisimulation equivalence
Proposition 5. A morphism of polygons with labels
Let S be a polygon over M(E,I). Label function λ: E→Λ is a map such that
(a1,a2)∈I ⇒ λ (a1)≠ λ (a2 ).
Let A=(S,M(E,I),s0 , Λ, λ) be a polygon over M(E,I) with a label function. An element
s∈S is reachable if (∃μ∈M(E,I)) s= s0 μ . Let S(s0 ) the set of reachable s.
Definition. A morphism of polygons with label functions A→A’ is open, if it is given by
a pair of (total) maps σ: S→S’, η: E→E’ , satisfying the following conditions
σ(s0)= s’0 ,
η save labels, i.e. λ’ °η = λ.
(e1,e2)∈I ⇒ (η(e1),η (e2) ∈I’
if s is reachable, then η: {s | se ∈S} → {e’ | σ(s)e’ ∈S’} surjective
if s is reachable, then η: {(e1,e2)∈I | se1e2 ∈S} → {(e’1,e’2)∈I’ | σ (s)e’1e’2 ∈S’} is surjective
Слайд 30Connection with bisimulation equivalence
Theorem. If pointed polygons A and A’ with
Pointed polygons A1 and A2 with labels in Λ are bisimulation equivalent if there is a pointed polygon A and open morphisms A1 ← A → A2.
Consider the following complex LΛ:
Label function gives the chain morphism
Слайд 31Example of trace equivalent asynchronous systems which are not bisimulation equivalent
E={a1, a2 ,b, c}, E’={a ,b, c}
λ(a1)= λ(a2)= a λ’(a)= a
λ(b)=b λ’(b)=b
λ(c)=c λ’(c)=c
Trace ab and ac.
Complexes
Слайд 32Perspectives
Studying the homotopical colimits of diagrams on the categories of partial
Applications of the homology groups for the studying the topology of state spaces of concurrent systems