620219,
Уральский госуниверситет
Главный проспект, 51, Екатеринбург, 620083
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Термодинамика суперионных проводников презентация
Содержание
- 1. Термодинамика суперионных проводников
- 2. Суперионные проводники Коэффициент диффузии в суперионных проводниках
- 3. Диффузия. Основные формулы.
- 4. ЭДС электрохимических ячеек
- 5. Типичная изобарно-изотерическая зависимость ЭДС электрохимической ячейки для
- 6. Термодинамические функции
- 7. Парциальные вклады в термодинамические функции
- 8. Ионный вклад
- 9. Структура дихалькогенидов титана МxTiX2, X=S,Se,Te Красный
- 10. Интеркалация щелочных металлов Интеркалация щелочных металлов
- 11. Термодинамические функции AgxTiS2, стадии 1 Верхний
- 12. Энтальпия ионной, электронной и атомной подсистем AgxTiS2,
- 13. Упругий вклад в свободную энергию интеркалированного иона
- 14. Энтальпия подвижных ионов с учётом упругого вклада
- 15. Энтальпия активации подвижного иона
- 16. Выводы Правильное описание энтальпии подвижных ионов требует
Слайд 1Термодинамика суперионных проводников
А.Н.Титов
Институт физики металлов УрО РАН
Ул. C. Ковалевской, 18, Екатеринбург,
Слайд 2Суперионные проводники
Коэффициент диффузии в суперионных проводниках D ~ 10-5 cm2/sec (это
коэффициент диффузии молекулы сахара в горячем чае или тяжёлых газов, типа HSe, при комнатной температуре);
Коэффициент диффузии в твёрдых телах вдали от температуры плавления D ~ 10-12 – 10-15 cm2/sec
Известны суперионнные проводники с проводимостью по ионам H, Li, Na, K, Cu, Rb, Ag, Cs, O, F, Cl.
Типичные представители: Li2S, CuBr, AgI, Bi2O3, CaF.
Коэффициент диффузии в твёрдых телах вдали от температуры плавления D ~ 10-12 – 10-15 cm2/sec
Известны суперионнные проводники с проводимостью по ионам H, Li, Na, K, Cu, Rb, Ag, Cs, O, F, Cl.
Типичные представители: Li2S, CuBr, AgI, Bi2O3, CaF.
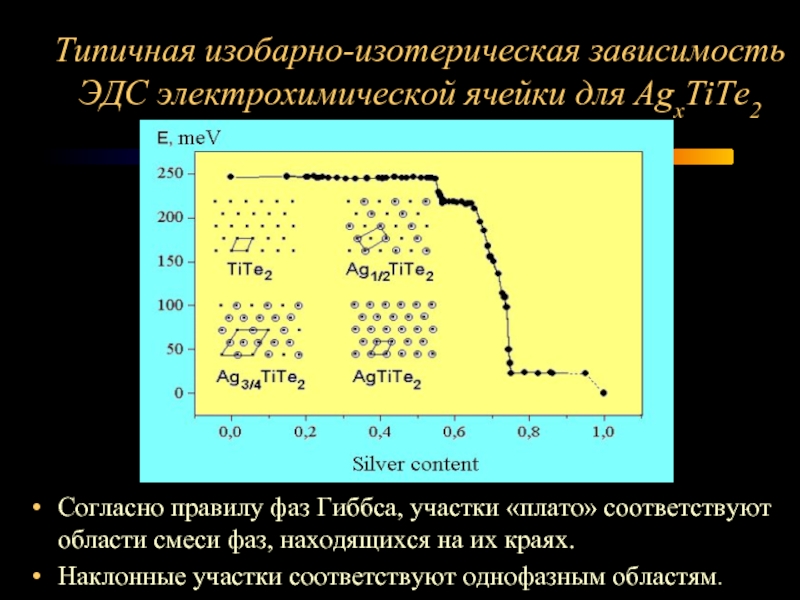
Слайд 5Типичная изобарно-изотерическая зависимость ЭДС электрохимической ячейки для AgxTiTe2
Согласно правилу фаз Гиббса,
участки «плато» соответствуют области смеси фаз, находящихся на их краях.
Наклонные участки соответствуют однофазным областям.
Наклонные участки соответствуют однофазным областям.
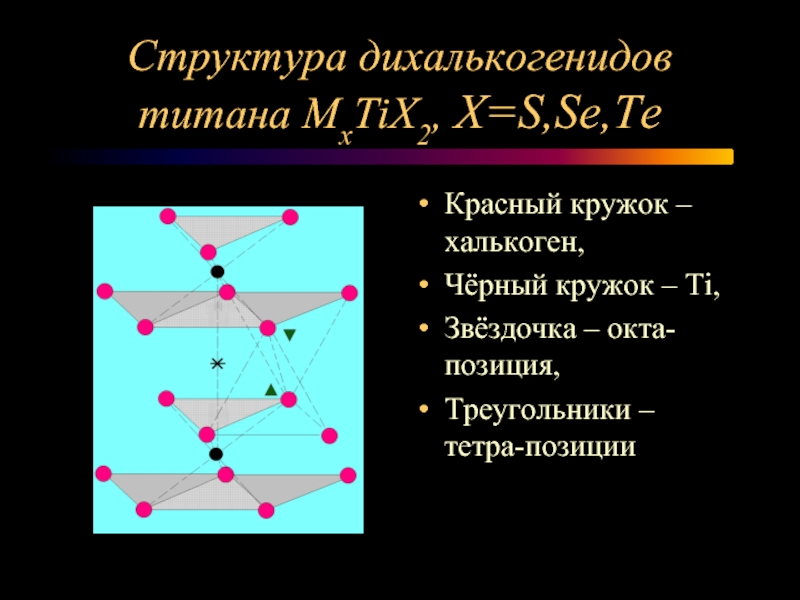
Слайд 9Структура дихалькогенидов титана МxTiX2, X=S,Se,Te
Красный кружок – халькоген,
Чёрный кружок
– Ti,
Звёздочка – окта-позиция,
Треугольники – тетра-позиции
Звёздочка – окта-позиция,
Треугольники – тетра-позиции
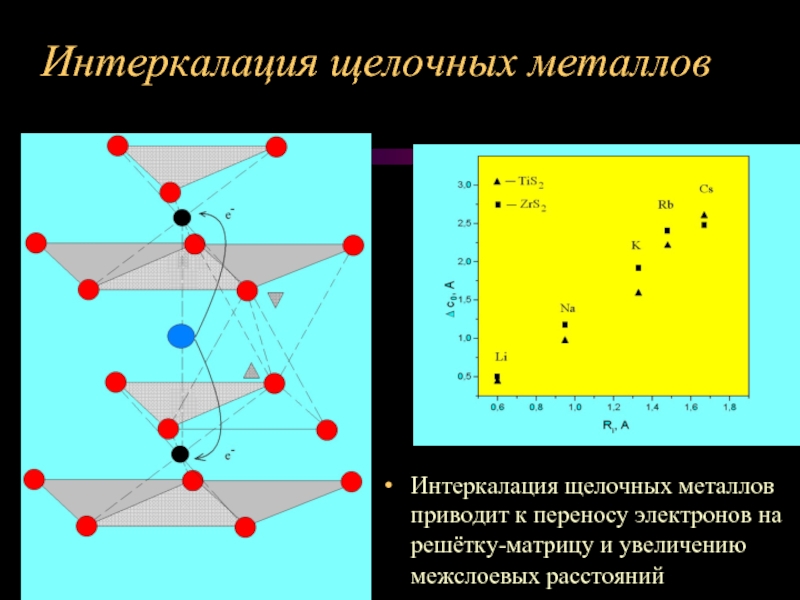
Слайд 10Интеркалация щелочных металлов
Интеркалация щелочных металлов приводит к переносу электронов на
решётку-матрицу и увеличению межслоевых расстояний
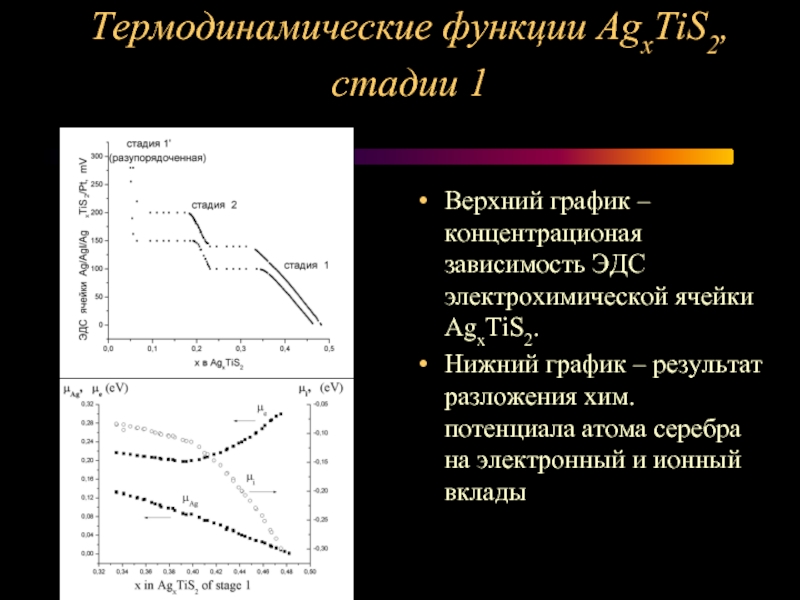
Слайд 11Термодинамические функции AgxTiS2, стадии 1
Верхний график – концентрационая зависимость ЭДС
электрохимической ячейки AgxTiS2.
Нижний график – результат разложения хим. потенциала атома серебра на электронный и ионный вклады
Нижний график – результат разложения хим. потенциала атома серебра на электронный и ионный вклады
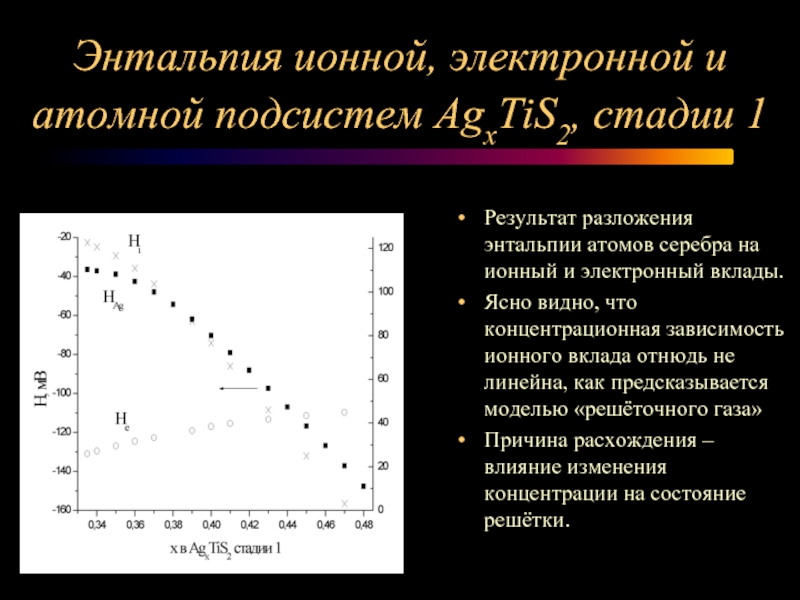
Слайд 12Энтальпия ионной, электронной и атомной подсистем AgxTiS2, стадии 1
Результат разложения
энтальпии атомов серебра на ионный и электронный вклады.
Ясно видно, что концентрационная зависимость ионного вклада отнюдь не линейна, как предсказывается моделью «решёточного газа»
Причина расхождения – влияние изменения концентрации на состояние решётки.
Ясно видно, что концентрационная зависимость ионного вклада отнюдь не линейна, как предсказывается моделью «решёточного газа»
Причина расхождения – влияние изменения концентрации на состояние решётки.
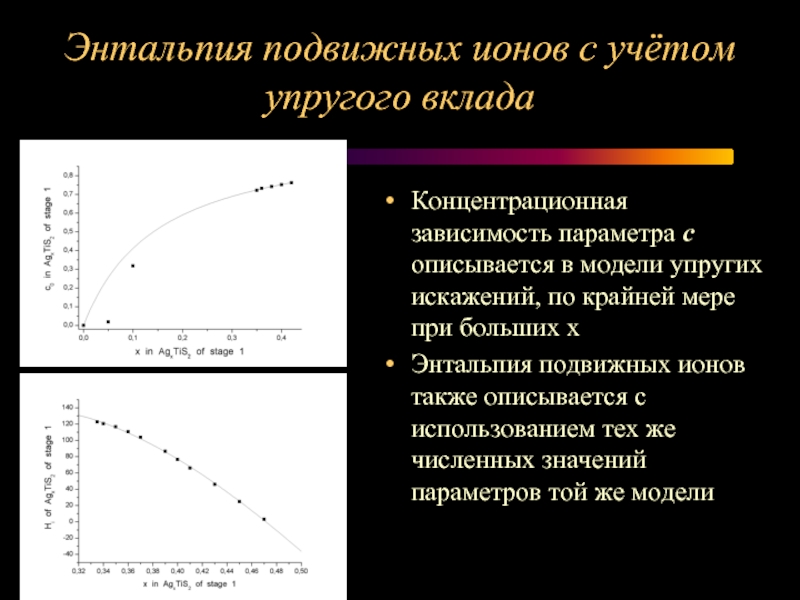
Слайд 14Энтальпия подвижных ионов с учётом упругого вклада
Концентрационная зависимость параметра с описывается
в модели упругих искажений, по крайней мере при больших х
Энтальпия подвижных ионов также описывается с использованием тех же численных значений параметров той же модели
Энтальпия подвижных ионов также описывается с использованием тех же численных значений параметров той же модели
Слайд 16Выводы
Правильное описание энтальпии подвижных ионов требует учёта упругого вклада от взаимодействия
подвижных ионов с жёстким остовом.
Энергия активации диффузии, по крайней мере в первом приближении, определяется не самими взаимодействиями подвижных ионов, но результатом конкуренции упругого вклада и вклада взаимодействия с ближайшим окружением, имеющего, по-видимому, ковалентную природу.
Энергия активации диффузии, по крайней мере в первом приближении, определяется не самими взаимодействиями подвижных ионов, но результатом конкуренции упругого вклада и вклада взаимодействия с ближайшим окружением, имеющего, по-видимому, ковалентную природу.