- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория телетрафика в мультисервисных сетях. Потоки вызовов. Классификация моделей. (Лекция 2) презентация
Содержание
- 1. Теория телетрафика в мультисервисных сетях. Потоки вызовов. Классификация моделей. (Лекция 2)
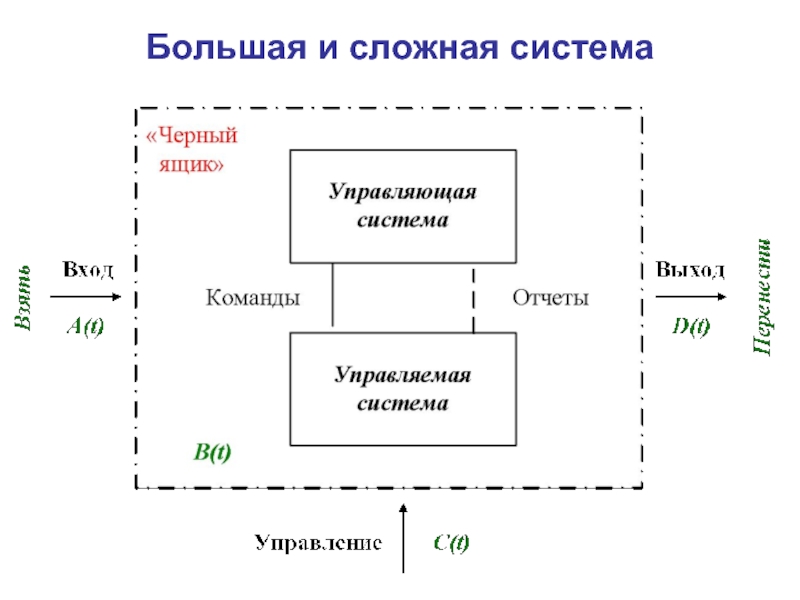
- 2. Большая и сложная система
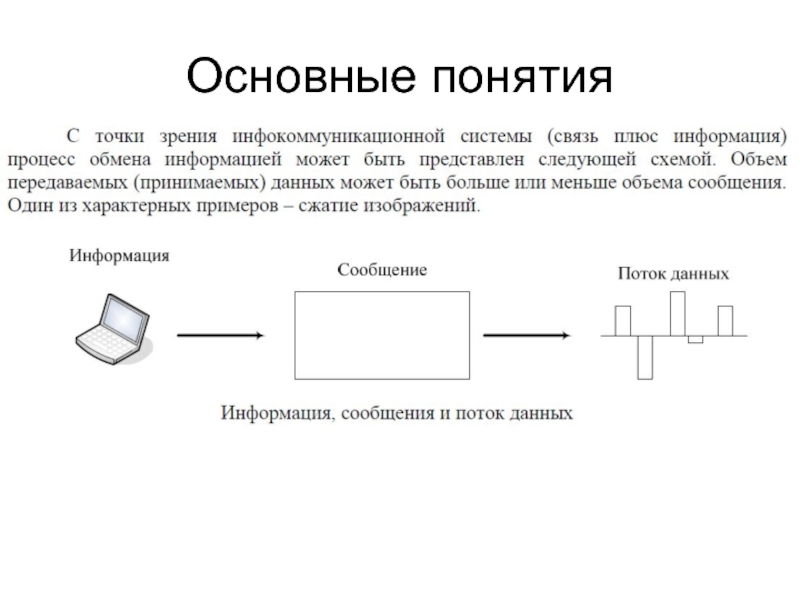
- 3. Основные понятия
- 4. Потоки заявок Процесс поступления заявок обычно является
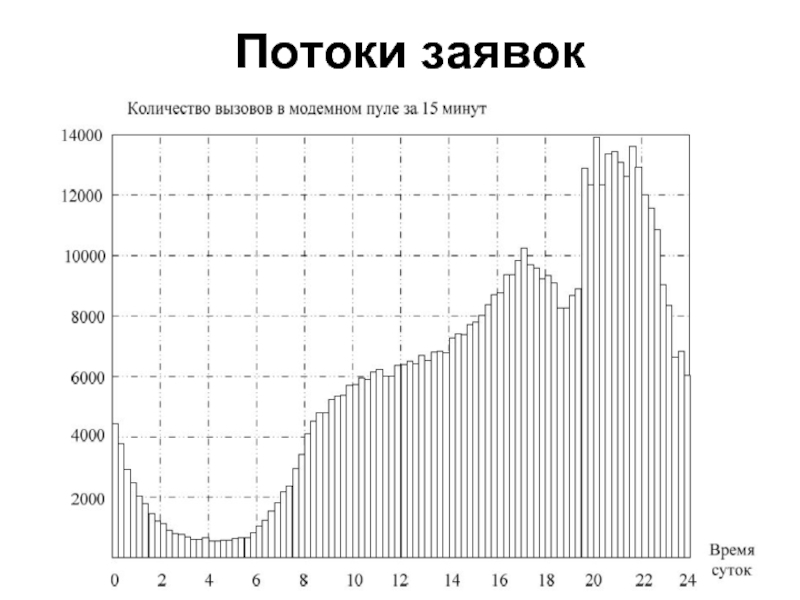
- 5. Потоки заявок
- 6. Потоки заявок Поток заявок – последовательность поступления
- 7. Потоки заявок Промежутки между вызовами: Zn=tn-tn-1 Момент
- 8. Способы задания потоков При помощи наступления
- 9. Потоки заявок
- 10. Свойства потоков Стационарность. Поток называется стационарным,
- 11. Стационарность
- 12. Последействие. Свойства потоков Поток вызовов является потоком
- 13. Последействие.
- 14. Свойства потоков Ординарность Поток вызовов называется ординарным,
- 15. Свойства потоков Потоки вызовов Случайные Неслучайные Стационарность
- 16. Характеристики потоков Ведущая функция потока - Λ[0;t)
- 17. Ведущая функция потока Λ[0;t) – это математическое
- 18. Интенсивность потока Мгновенная интенсивность потока - λ(t)
- 19. Параметр потока Параметр случайного потока вызовов -
- 20. Параметр потока Стационарный поток В отличие от
- 21. Простейший поток Простейший поток – это стационарный,
- 22. Простейший поток Среднее число заявок, поступающих за
- 23. Алгоритмы обслуживания заявок
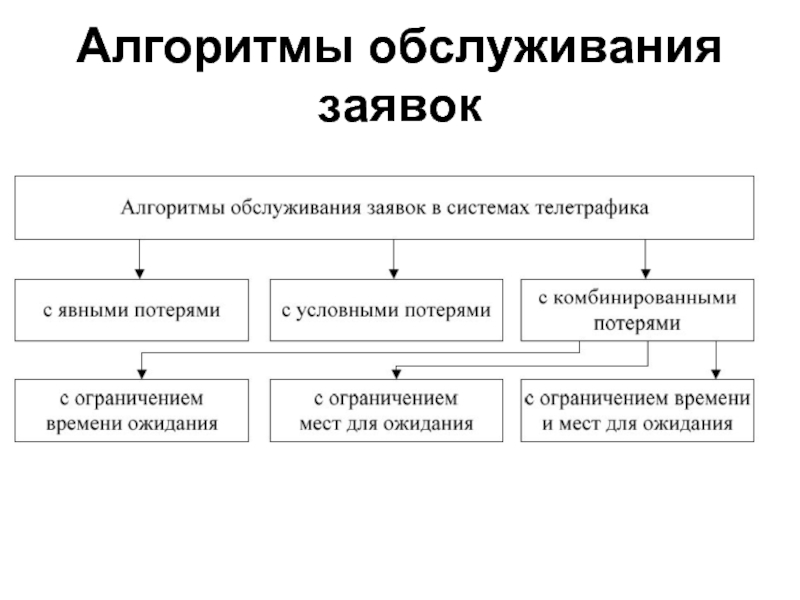
- 24. Алгоритмы обслуживания заявок
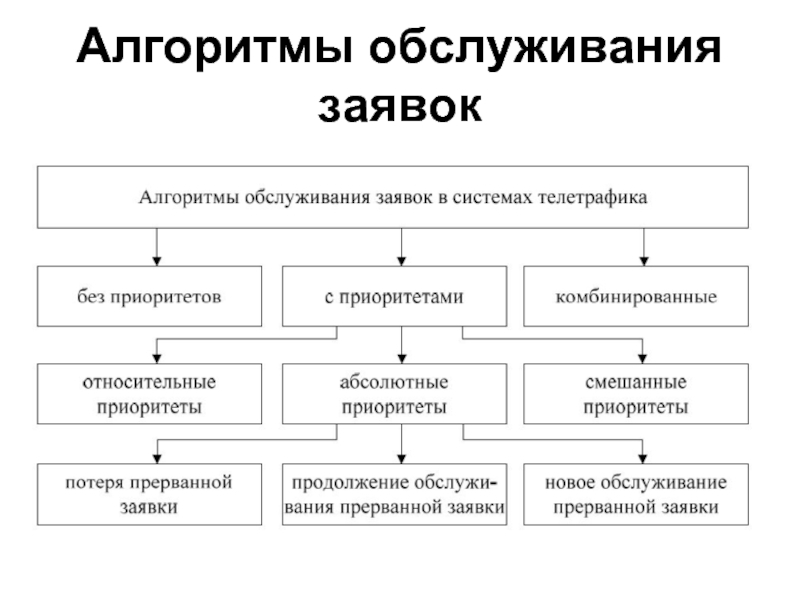
- 25. Алгоритмы обслуживания заявок
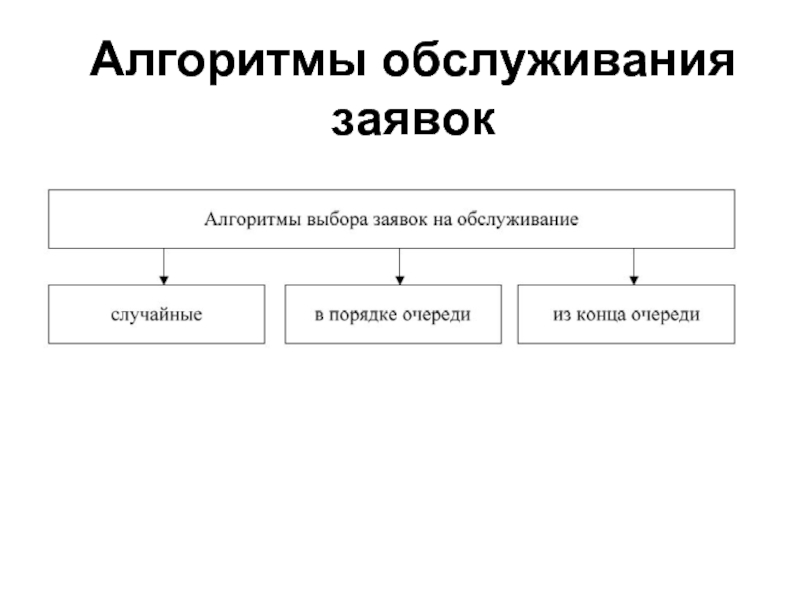
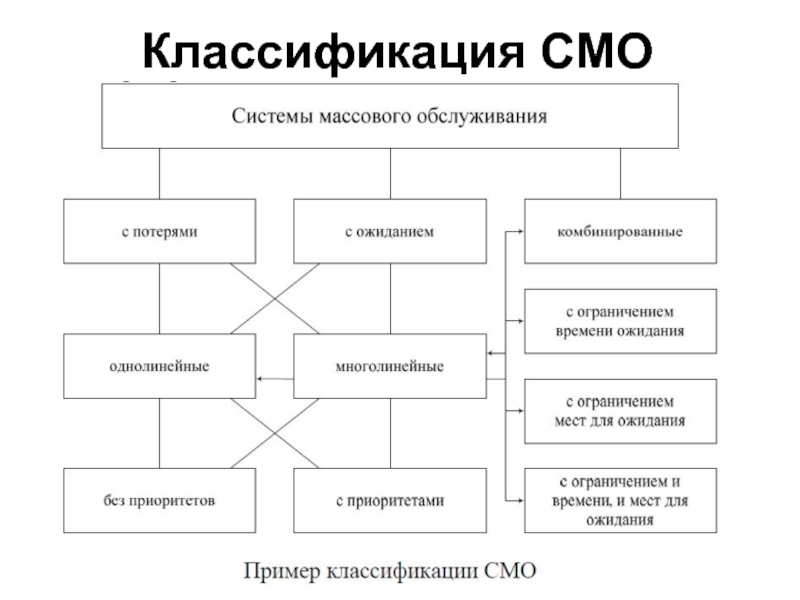
- 26. Классификация СМО
- 27. Классификация СМО A(x) | B(x) | v
- 28. Типы трафика в мультисервисных сетях
- 29. Использованные источники Мышкис А.Д. Элементы теории
- 30. Вопросы?
Слайд 1Теория Телетрафика в мультисервисных сетях Лекция №2 «Потоки Вызовов. Классификация моделей.» доцент,
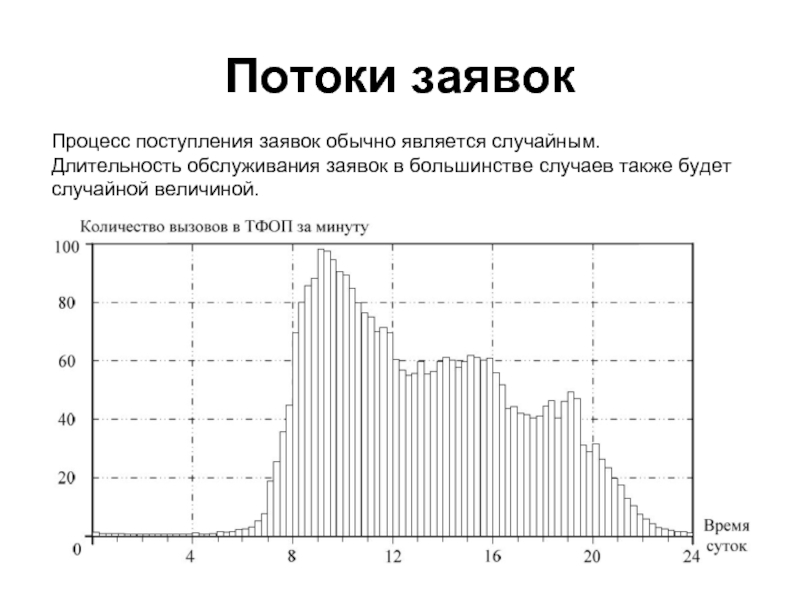
Слайд 4Потоки заявок
Процесс поступления заявок обычно является случайным. Длительность обслуживания заявок в
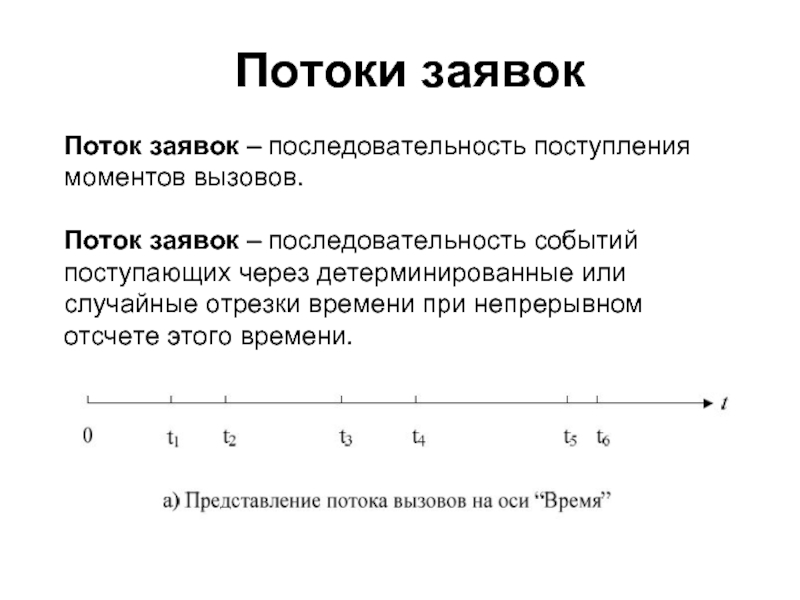
Слайд 6Потоки заявок
Поток заявок – последовательность поступления моментов вызовов.
Поток заявок – последовательность
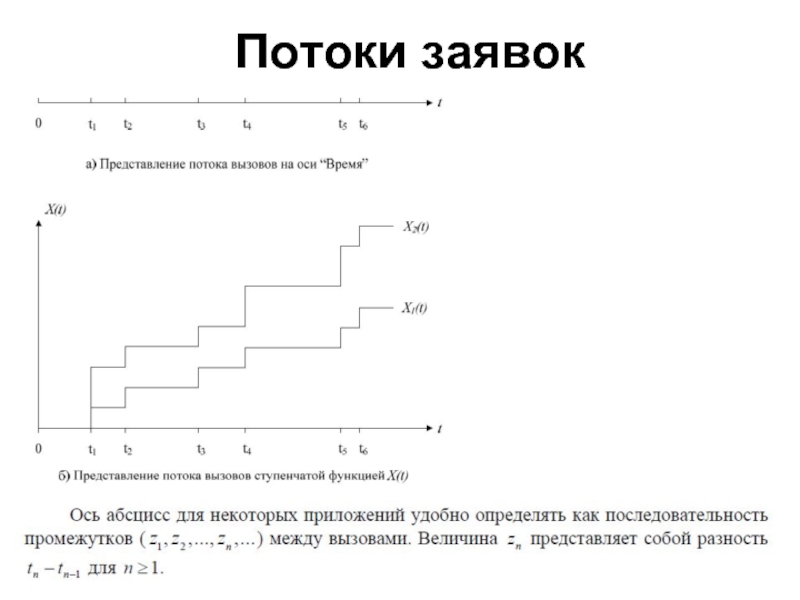
Слайд 7Потоки заявок
Промежутки между вызовами: Zn=tn-tn-1
Момент времени – число соответствующее промежутку времени
Слайд 8Способы задания потоков
При помощи наступления моментов вызовов:
t1 t2 t3 t4
При помощи задания промежутков между вызовами
Z1 Z2 Z3 Z4 ….. Zn
3. При помощи чисел Ki: K – количество вызовов поступающих за промежуток [0; t1]; [0; t2]; [0; tn]
Все три способа задания потоков - эквивалентны
Слайд 10Свойства потоков
Стационарность.
Поток называется стационарным, если вероятность поступления вызовов случайного потока или
Слайд 12Последействие.
Свойства потоков
Поток вызовов является потоком без последействия, если вероятность поступления вызовов
Таким образом для потока без последействия прошлая история не играет никакой роли для прогнозирования его будущего.
Слайд 14Свойства потоков
Ординарность
Поток вызовов называется ординарным, если вероятность поступления 2 и более
Практически ординарность потока означает невозможность поступления 2 и более вызовов в любой момент времени.
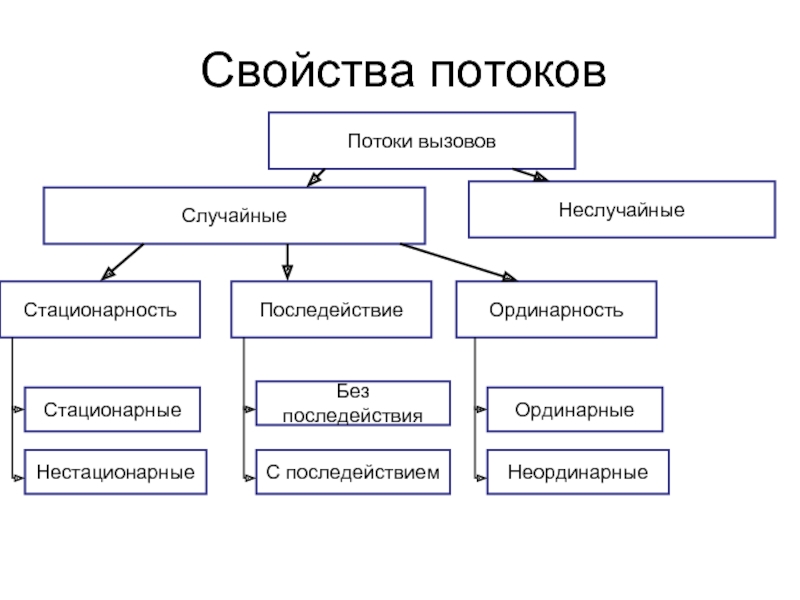
Слайд 15Свойства потоков
Потоки вызовов
Случайные
Неслучайные
Стационарность
Последействие
Ординарность
Стационарные
Нестационарные
Без последействия
С последействием
Ординарные
Неординарные
Слайд 16Характеристики потоков
Ведущая функция потока - Λ[0;t)
Интенсивность потока - λ
Параметр потока
Слайд 17Ведущая функция потока
Λ[0;t) – это математическое ожидание числа вызовов в интервале
Λ[0;t) – не отрицательная, не убывающая и в практических задачах принимает конечное значение.
Слайд 18Интенсивность потока
Мгновенная интенсивность потока - λ(t) - математическое ожидание числа вызовов,
Нестационарный поток
, если такой предел существует
Стационарный поток
λ – конечное значение математическое ожидание числа вызовов, поступающих в единицу времени.
Размерность: 1/t
Λ[0;t) = λ*t , из-за свойства аддитивности
Слайд 19Параметр потока
Параметр случайного потока вызовов - Π (t) – в момент
Параметр случайного потока вызовов определяет в момент времени – плотность вероятности наступления вызывающего момента.
Практически параметр случайного потока вызовов характеризует частоту наступления вызывающих моментов.
Слайд 20Параметр потока
Стационарный поток
В отличие от ведущей функции потока параметр потока характеризует
Кроме того поток вызовов относится не ко всему отрезку времени, а только к фиксированному моменту времени.
Слайд 21Простейший поток
Простейший поток – это стационарный, ординарный поток без последействия
Описать поток
Распределение Пуассона
Функция распределения промежутков времени между вызовами
Экспоненциальное распределение
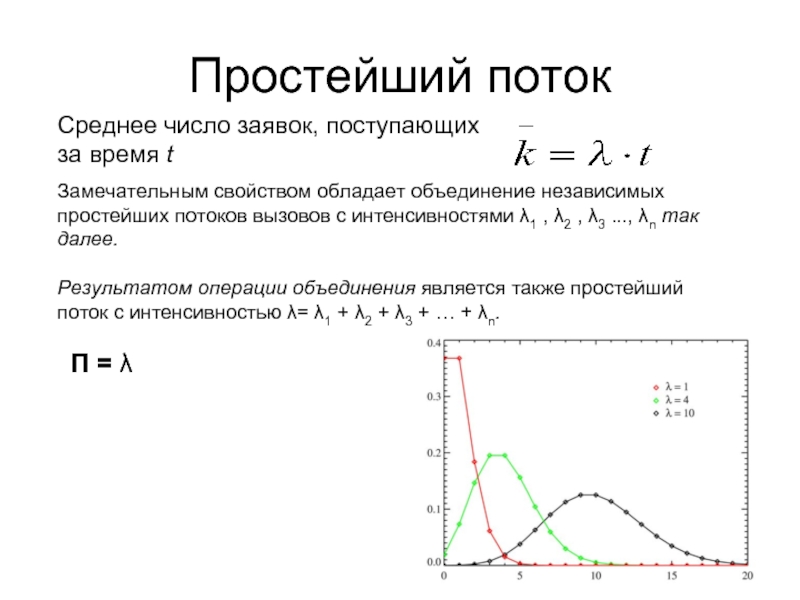
Слайд 22Простейший поток
Среднее число заявок, поступающих за время t
Замечательным свойством обладает объединение
Результатом операции объединения является также простейший поток с интенсивностью λ= λ1 + λ2 + λ3 + … + λn.
Π = λ
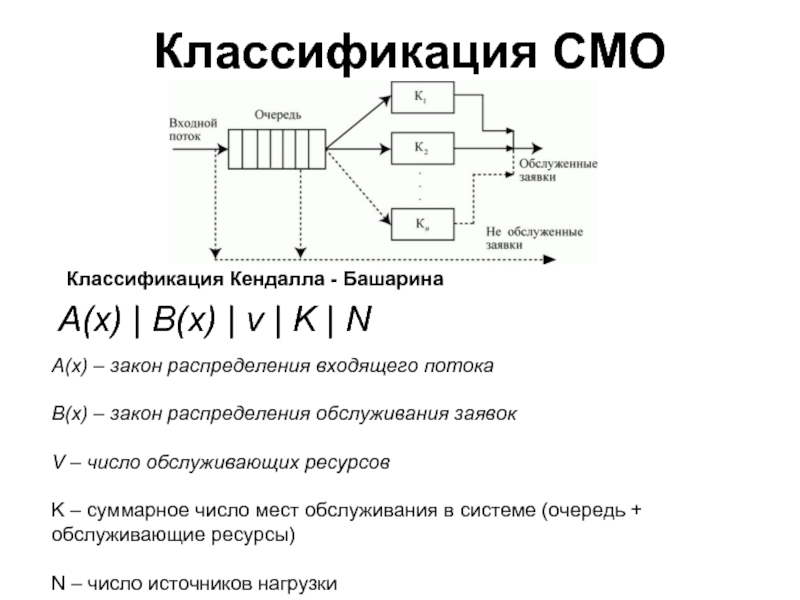
Слайд 27Классификация СМО
A(x) | B(x) | v | K | N
Классификация Кендалла
A(x) – закон распределения входящего потока
B(x) – закон распределения обслуживания заявок
V – число обслуживающих ресурсов
K – суммарное число мест обслуживания в системе (очередь + обслуживающие ресурсы)
N – число источников нагрузки
Слайд 29Использованные источники
Мышкис А.Д. Элементы теории математических моделей. – М.: Книжный
Маликов Р.Ф. Основы математического моделирования. – М.: Горячая линия – Телеком, 2010.
Качала В.В. Основы теории систем и системного анализа. – М.: Горячая линия – Телеком, 2007.
Городецкий А.Е., Дубаренко В.В., Тарасова И.Л., Шереверов А.В. Программные средства интеллектуальных систем. – СПб.: Изд-во СПбГТУ, 2000.
Тарасенко Ф.П. Прикладной системный анализ. – М.: КНОРУС, 2010.
Кондаков Н.И. Логический словарь-справочник. – М.: Наука, 1976.
Энциклопедии и словари.
Ресурсы Internet.