Тамбовский государственный технический университет
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ПРАКТИЧЕСКИЕ АСПЕКТЫ ПОСТРОЕНИЯ РЕГИОНАЛЬНЫХ ОБРАЗОВАТЕЛЬНЫХ КОМПЬЮТЕРНЫХ СЕТЕЙ презентация
Содержание
- 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ПРАКТИЧЕСКИЕ АСПЕКТЫ ПОСТРОЕНИЯ РЕГИОНАЛЬНЫХ ОБРАЗОВАТЕЛЬНЫХ КОМПЬЮТЕРНЫХ СЕТЕЙ
- 2. Термины и сокращения РОКС - региональная
- 3. Предпосылки создания РОКС РОКС АСНИ АОС ИАИС Информационные ресурсы 2
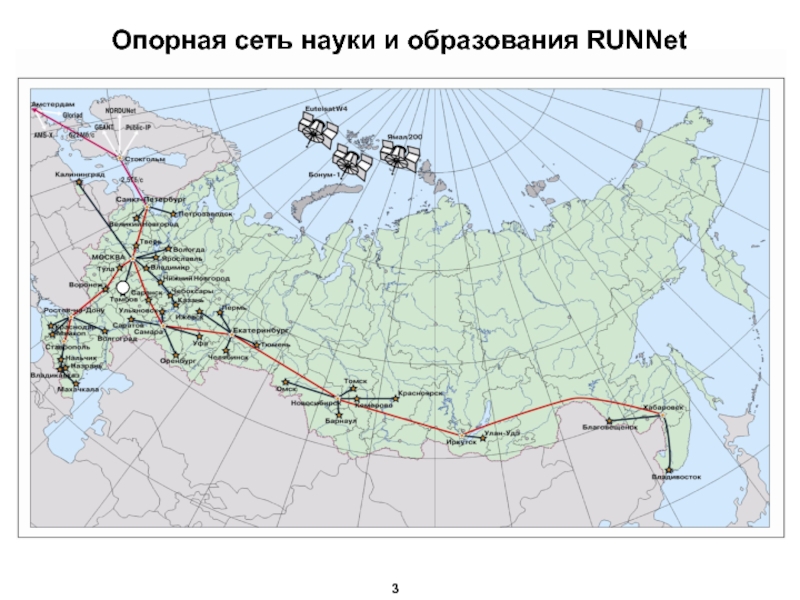
- 4. Опорная сеть науки и образования RUNNet 3
- 5. Схема связности РРЦ регионов ЦФО 2
- 6. Беспроводная составляющая сети TSTUNet 5
- 7. Проблемы в развитии сети
- 8. Недостатки применения существующих методов моделирования компьютерных
- 9. Цель работы Наиболее полное удовлетворение образовательного
- 10. Задачи Разработка новых теоретических основ
- 11. Объект исследования Региональные образовательные компьютерные сети
- 12. Состояние вопроса о математическом моделировании компьютерных сетей
- 13. Сложность вычислений Сложность Алгоритмическая
- 14. Предпосылки перехода от качественного к количественному
- 15. Структурная сложность орграфа Цель анализа: упорядочение
- 16. где - множество вершин;
- 17. - число контуров - число
- 18. Взвешенный орграф – совокупность трёх множеств:
- 19. Формируем матрицу контуров
- 20. Матричные представления взвешенного орграфа Взвешенная матрица
- 21. 1 2
- 22. Матрица сложности 21
- 23. Структурная сложность графа с дугой,
- 24. 2 1 7 2 5
- 25. Структурная сложность замкнутых детерминированных систем Новые формальные операторы: 24
- 26. Формальное представление системы Множество дуг системы: Множество
- 27. Определение подсистемы 26
- 28. Формальное определение абстрактной системы Аксиома уникальности
- 29. Нулевая структурная сложность: Структурная сложность
- 30. Сложение: Умножение: Единичная сложность: Алгебра структурной сложности (продолжение) 29
- 32. Лексиграфический порядок в иерархии разрывов 31
- 33. …
- 34. Множество контуров системы: Аспекты вычисления критерия структурной
- 35. Оператор структурной декомпозиции 34 Матрица достижимости
- 36. 35
- 37. Критерий оценки структурной сложности замкнутой системы Пример:
- 38. 37 75 f2 f4 1 3
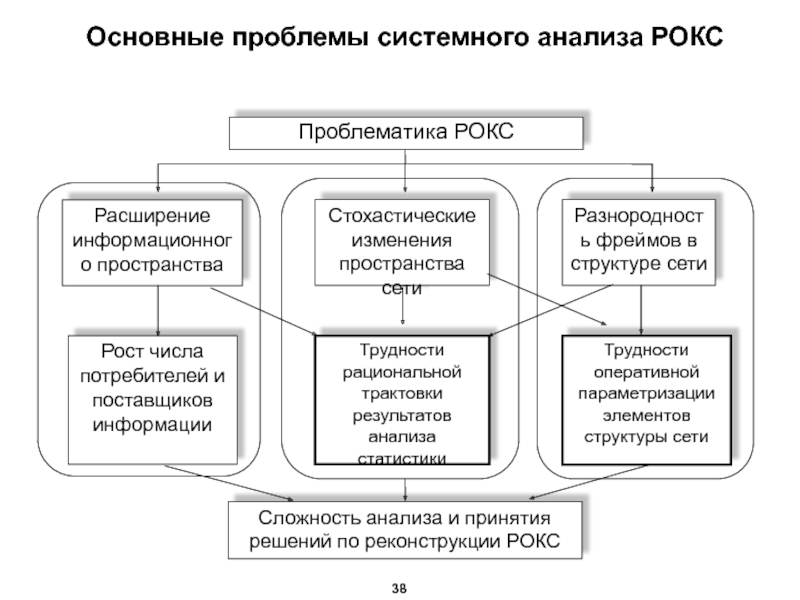
- 39. Основные проблемы системного анализа РОКС 38
- 40. Тенденции решения проблем системного анализа РОКС 39
- 41. с дискретизацией из
- 42. Внешние связи РОКС Входящий трафик
- 43. структурной
- 44. Особенности РОКС порождают матричный критерий сложности
- 45. Стохастическая структурная сложность РОКС - это случайная
- 46. Параметризация структуры РОКС – тренд –
- 47. Иллюстрация к задаче о реконструкции РОКС Определить
- 48. Иллюстрация к задаче о реконструкции 47
- 49. Основные научные результаты Разработаны теоретические
- 50. Диаграмма роста информационной энтропии Тамбовской РОКС на периоде решения задачи о реконструкции 49
- 51. Орграф ядра сети TSTUNet 1 – Ленинградская,
- 52. Матрица смежности орграфа ядра сети TSTUNet 51
- 53. Площадка 3 ТГТУ, ул. Советская, 106 ТГУ
- 54. Практическая ценность проведенных исследований Применение разработанных
- 55. Внедрение и апробация Результаты работы докладывались более
- 56. Разработаны теоретические основы построения критериев структурной сложности
Слайд 1ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ПРАКТИЧЕСКИЕ АСПЕКТЫ ПОСТРОЕНИЯ РЕГИОНАЛЬНЫХ ОБРАЗОВАТЕЛЬНЫХ КОМПЬЮТЕРНЫХ СЕТЕЙ
Подольский В.Е.,
Слайд 2Термины и сокращения
РОКС - региональная образовательная компьютерная сеть
ТГТУ -
АСНИ - автоматизированная система научных исследований
АОС - автоматизированная обучающая система
ИАИС - интегрированная автоматизированная информационная система
TWN - Тамбовская беспроводная сеть
РРЦ - региональный ресурсный центр
РЕОИС - развитие единой образовательной информационной среды
ЛВС - локальная вычислительная сеть
ФРЦ - федеральный ресурсный центр
ИКТ - информационно-коммуникационные технологии
ММ - математическая модель
ЦФО - Центральный федеральный округ
1
Слайд 7Проблемы в развитии сети
Рост числа пользователей и их потребностей в
Резкое усложнение процессов обработки информации о текущем состоянии РОКС
Необходимость повышения эффективности отслеживания текущего состояния сети большой размерности для обеспечения высокого качества обслуживания клиентов
Обоснование затрат на реконструкцию РОКС
Необходимость построения систем моделирования РОКС с ограниченной вычислительной сложностью и возможностями использования распределенных вычислений на внутренней сетевой основе
6
Слайд 8
Недостатки применения существующих методов моделирования компьютерных сетей к РОКС:
Неадекватность трафика закону
ρ
пакеты информации
σ² = ∞ ?
Математическое моделирование конкретной сети имеет частный характер, требует значительного времени на разработку и больших вычислительных ресурсов на выявление практически значимых особенностей функционирования этой сети
время
неактуальность
разработка
…..расчеты…..
Состояние сети большой размерности описывается множеством наблюдаемых и расчетных величин
?
Не используются возможности сетей для распараллеливания вычислений при их моделировании
7
Слайд 9Цель работы
Наиболее полное удовлетворение образовательного
сообщества сетевыми услугами при минимизации затрат
на содержание
оценок структурной сложности.
8
Слайд 10Задачи
Разработка новых теоретических основ для нахождения оценок структурной сложности технических систем
Формирование критериев оценки структурной сложности в применении к решению задач реконструкции и стабилизации качества обслуживания региональных образовательных компьютерных сетей.
Разработка типовых подходов к построению региональных образовательных компьютерных сетей с точки зрения практической реализации
Создание поддерживающей организационной инфраструктуры региональных образовательных компьютерных сетей.
Определение условий унификации действующей Тамбовской региональной образовательной компьютерной сети как типовой для других регионов России.
9
Слайд 11Объект исследования
Региональные образовательные компьютерные сети в условиях интенсивного роста численности пользователей,
Предмет исследования
Математические методы и модели, описывающие состояние компьютерной сети большой размерности, способствующие принятию оперативных решений по качеству обслуживания и реконструкции в условиях непрерывного функционирования сети.
10
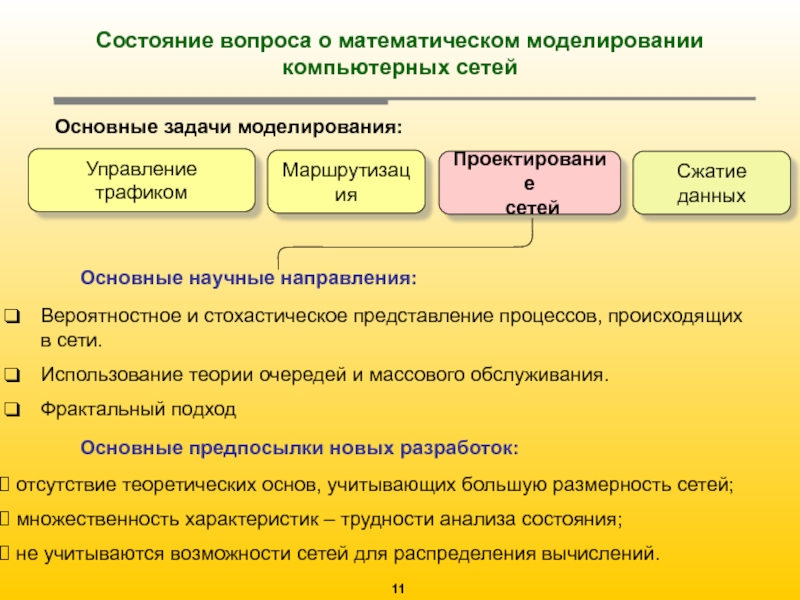
Слайд 12Состояние вопроса о математическом моделировании компьютерных сетей
Основные задачи моделирования:
Управление трафиком
Маршрутизация
Проектирование
сетей
Сжатие данных
Основные научные направления:
Вероятностное и стохастическое представление процессов, происходящих в сети.
Использование теории очередей и массового обслуживания.
Фрактальный подход
Основные предпосылки новых разработок:
отсутствие теоретических основ, учитывающих большую размерность сетей;
множественность характеристик – трудности анализа состояния;
не учитываются возможности сетей для распределения вычислений.
11
Слайд 13
Сложность
вычислений
Сложность
Алгоритмическая
сложность
Теория сложности
Структурная сложность
Термодинамическая сложность (И.Пригожин)
Информационная энтропия
…
t
Состояние технической системы
12
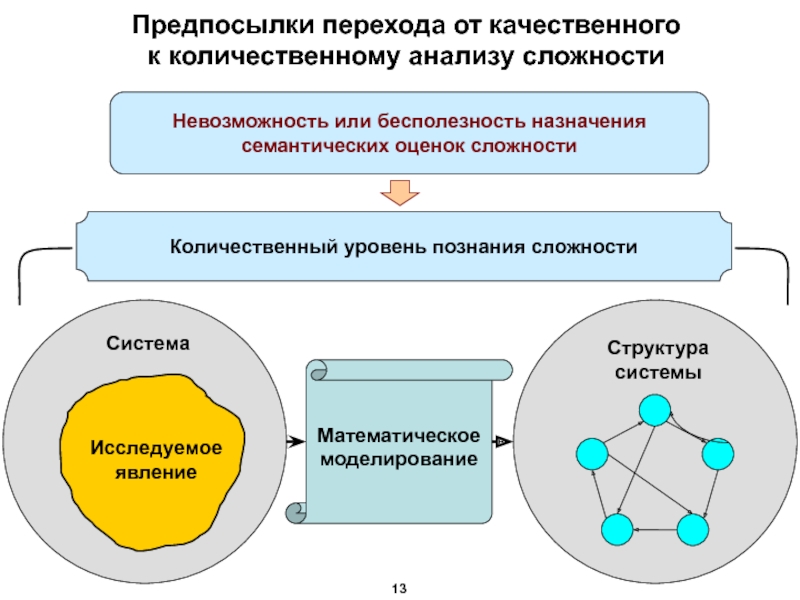
Слайд 14Предпосылки перехода от качественного
к количественному анализу сложности
Невозможность или бесполезность назначения
семантических оценок сложности
Количественный уровень познания сложности
Исследуемое явление
Система
Математическое
моделирование
Структура системы
13
Слайд 15
Структурная сложность орграфа
Цель анализа: упорядочение орграфов по критерию структурной сложности
Шкала структурной
14
Слайд 16
где
- множество вершин;
- множество дуг.
Сортировка орграфов:
- структурная сложность
аксиоматика
Формализация понятия «орграф»
15
Слайд 18
Взвешенный орграф – совокупность трёх множеств:
вес дуг
Матричные представления орграфа
17
Матрица смежности:
Матрица достижимости:
,
6
Если
1
2
3
4
5
6
7
8
9
2
3
4
5
7
8
9
2
3
4
5
6
7
8
9
1
1
граф сильно связный
Матрица
инцидентности:
1
2
4
3
+1
4
1
2
3
4
5
6
7
1
2
3
+1
-1
-1
-1
-1
-1
-1
-1
+1
+1
+1
+1
Слайд 19
Формируем матрицу контуров
23
Пример:
Выявление контуров в орграфе
Находим множество контуров
Структурная сложность кольца из
18
Слайд 20
Матричные представления взвешенного орграфа
Взвешенная матрица смежности
19
i
j
Отток информации
k
j
-1
+1
i
j
0
-1
+1
0
i
k
Взвешенная матрица инцидентности
,
Дуги упорядочены в порядке возрастания числа вхождений в контуры
Дуга с наибольшим приоритетом
2
1
7
5
2
5
3
8
1
2
7
1
8
2
3
4
5
6
7
2
1
9
8
2
1
11
15
3
Взвешенная матрица контуров
Слайд 21
1
2
Взвешенная матрица
смежности X
Взвешенная матрица
инцидентности B
Взвешенная
транспонированная
матрица контуров С*
(n x n)
(n x
(m x K)
(n x m)
(n x K)
Структурная сложность взвешенного орграфа
20
Для не взвешенных сильно связных орграфов
XBC*=0
1)
γi=idem
2)
j: γj > γk, k ≠ j, 1 ≤ k ≤ n
XBC* ≠ 0
Слайд 22
Матрица сложности
21
Критерий сложности взвешенного орграфа
, где
- спектр матрицы сложности;
9
1
2
8
5
4
3
7
6
Всегда ли имеет
Познание сложного через упрощение
Гамак
Критическая дуга
Слайд 23
Структурная сложность графа с дугой, получившей приращение
Мера приоритетности дуги
30
22
Наиболее приоритетная дуга
Слайд 24
2
1
7
2
5
3
8
1
2
7
1
8
2
3
4
5
6
7
2
1
9
8
2
1
11
15
5
3
1
2
3
4
5
6
7
8
1
9
10
11
2
16
3
1.025
Индекс наибольшей приоритетности
в матрице C
Структурная бифуркация
при увеличении веса дуги,
имеющей наивысший
Диаграмма приоритетности дуг,
упорядоченных по числу вхождений
в контуры орграфа и по весу
Матричный критерий S(G) позволяет оценивать
сложность взвешенного орграфа. С его помощью выявляется дуга с наивысшей приоритетностью,
указывающая на наискорейший путь упрощения графа с целью познания его структурной сложности
Вычисление приоритетности дуг
23
Слайд 26Формальное представление системы
Множество дуг системы:
Множество достижимостей системы:
Условие сильной связности системы:
25
Слайд 28
Формальное определение абстрактной системы
Аксиома уникальности абстрактных систем:
Параметризованная система:
Аналогия с орграфами:
27
Слайд 29Нулевая структурная сложность:
Структурная сложность системы
если система не содержит ни одной сильно связной подсистемы
Алгебра структурной сложности
Формализация структурной сложности
28
Для количественной оценки структурной сложности необходимо
найти дескрипторы, непротиворечиво декларирующие искомую
шкалу сложности, которая, в свою очередь, отображает меру
достижимости цели анализа системы .
Основными дескрипторами шкалы структурной сложности
являются аксиоматика и алгебра структурной сложности.
Слайд 31
1
Сильно связные подсистемы
2
3
Нижний уровень
рекурсии
Возможные варианты состояния системы после разрыва итератора
30
Слайд 33
…
…
…
…
…
П
О
Д
С
И
С
Т
Е
М
Ы
…
…
…
…
…
…
П
О
Д
С
И
С
Т
Е
М
Ы
…
Расчет
подсистемы
завершен
Иерархия расчетного модуля сложной технической системы
32
Расчетным модулем
для получения всех выходных переменных ММ Out(fi), i=1..n на компьютерах вычислительного кластера
Слайд 34Множество контуров системы:
Аспекты вычисления критерия структурной сложности
33
Матрица контуров
Контурность дуги
Контурал
1
1
1
Σ
Дуга
Контурион
Слайд 35
Оператор структурной декомпозиции
34
Матрица достижимости
После разрыва итератора оператор структурной декомпозиции выявляет сильно
Слайд 37Критерий оценки структурной сложности замкнутой системы
Пример:
36
3а
2
3б
1
4
20
5
3
3
3
2
1
1
10
4
2
5
6
1
5
Вес дуги, разрываемой первой
Остаточная сложность
Слайд 3837
75
f2
f4
1
3
f1
f6
f3
f2
f5
f4
f2
f7
f7
f8
f5
f8
f2
f4
f2
f1
f4
f3
f7
f5
f5
f6
f8
f1
f6
f7
f8
f3
f2
20
4
5
3
10
4
5
6
1
1
2
2
3
140
284
110
72
500
284
141
72
315
192
71
70
130
130
f1
5
9
5
5
4
4
3
3
3
3
3
2
2
2
1
1
1
140
110
72
72
70
75
175
Пример вычисления критерия структурной сложности (продолжение)
Слайд 41с дискретизацией из частей
Орграф динамического развития РОКС:
Множество
Множество дуг без учета внешних связей РОКС:
Период прогнозирования:
Формализация структуры РОКС
40
Слайд 42Внешние связи РОКС
Входящий трафик
Исходящий трафик
41
Ini
Outi
vi
Φ
vi
vi
Ini
Outi
Внутренние
связи
i-го узла
Слайд 43
структурной сложности
Политика оперативного управления РОКС
должна обеспечивать минимальное изменение
на периоде времени
Оперативное
42
Балансовое ограничение
Финансовое ограничение
Слайд 44Особенности РОКС порождают матричный критерий сложности
– критерий предпочтительности:
Критерий предпочтительности
Используется в
* - оптимальность иерархической кластеризации,
когда для решения крупных задач используются
все имеющиеся ресурсы региональной сети,
причем для связей между подзадачами
предпочтительными являются каналы наибольшей
мощности с наименьшей загрузкой
43
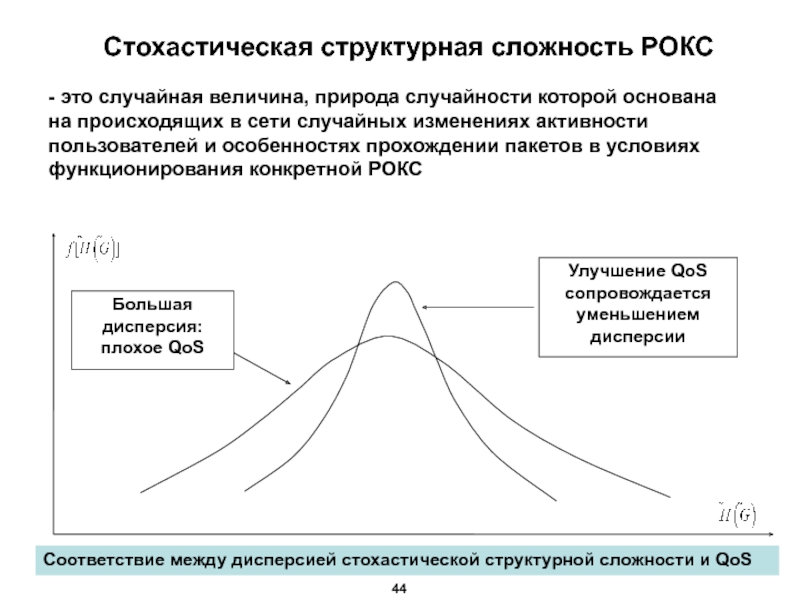
Слайд 45Стохастическая структурная сложность РОКС
- это случайная величина, природа случайности которой основана
Соответствие между дисперсией стохастической структурной сложности и QoS
44
Большая дисперсия: плохое QoS
Улучшение QoS сопровождается уменьшением дисперсии
Слайд 46Параметризация структуры РОКС
– тренд
– случайная составляющая
- вес дуги
–
к
– стоимость обслуживания линии связи
– оценка пропускной способности линии связи
– оценка пропускной способности выходного канала узла
45
Слайд 47Иллюстрация к задаче о реконструкции РОКС
Определить время проведения и состав ближайшей
РОКС при наличии трендов и флуктуаций пропускной
способности каналов связи, активности пользователей и
и контента сети
46
Слайд 48Иллюстрация к задаче о реконструкции
47
Начало прогноза
Прогноз времени реконструкции
Время эксплуатации РОКС
Интервал допустимых
Слайд 49Основные научные результаты
Разработаны теоретические основы построения критериев структурной
Сформулирован критерий структурной сложности взвешенных сильно связных орграфов, соответствующий целям математического моделирования региональных образовательных компьютерных сетей.
Разработаны методы и алгоритмы имитационного моделирования региональных образовательных компьютерных сетей, использующие новый подход на основе оценки структурной сложности системы большой размерности.
Найдены условия применения критерия оценки структурной сложности для решения задач развития и реконструкции региональных образовательных компьютерных сетей.
48
Слайд 50Диаграмма роста информационной энтропии Тамбовской РОКС на периоде решения задачи о
49
Слайд 51Орграф ядра сети TSTUNet
1 – Ленинградская, 1 (площадка 1),
2 –
50
13
9
5
10
11
12
7
1
3
14
6
4
2
8
Слайд 53Площадка 3
ТГТУ,
ул. Советская, 106
ТГУ им. Державина
ул. Интернациональная, 33
ул. Мичуринская
ул. Чичканова
Площадка 6
Телецентр,
ул.
Площадка 4
ТГТУ,
ул. Мичуринская, 112
ул. Советская
ул. Комсомольская
Площадка 7
ЮВТТК,
Привокзальная пл.,10
Площадка 2
ТГТУ,
ул. Советская, 116
Площадка 5
Тамбовгражданпроект
ул. Советская, 34
RB-net, РTK Internet
ул. Интернациональная
ул. Советская
Площадка 1
ТГТУ,
ул. Ленинградская, 1
Runnet
TWN
региональная компонента
Транстелеком
ТОИПКРО, Управление образования
ул. Советская, 108
RUNNet
RBNet,
РТКомм
RUNNet
TWN
Схема трассы волоконно-оптической линии связи
52
Слайд 54Практическая ценность проведенных исследований
Применение разработанных методов и алгоритмов
развития и
Практические результаты исследования постоянно используются при функционировании Тамбовской РОКС TSTUnet.
Создание поддерживающей организационной инфраструктуры РОКС в масштабах Тамбовской области.
Экономия средств на реконструкцию сети.
53
Слайд 55Внедрение и апробация
Результаты работы докладывались более чем на 60 международных, всероссийских
Имеются акты о внедрении от:
54
Слайд 56Разработаны теоретические основы построения критериев структурной сложности замкнутых детерминированных систем большой
Найдены условия применения теории структурной сложности для моделирования региональных образовательных компьютерных сетей, позволяющие упростить процедуру оценки их состояния до анализа одномерной величины в отличие от ранее известных методов, требующих большой вычислительной мощности и не использующих сети в режиме распределенных вычислений.
Разработаны методы и алгоритмы имитационного моделирования региональной образовательной компьютерной сети, использующие новый подход на основе оценки структурной сложности системы, что позволило снизить затраты на реконструкцию сети.
Сформулированы типовые технические подходы к построению региональных образовательных компьютерных сетей, открывающие новые возможности выбора рационального состава технических средств и особенностей телекоммуникаций при построении новых сетей и совершенствовании имеющихся. Типовые подходы использованы в работах по ФЦП «Развитие единой образовательной информационной среды».
Основные результаты исследования реализованы при развитии Тамбовской региональной образовательной компьютерной сети, которая может быть признана типовой, и отдельные элементы которой использованы при создании и развитии образовательных сетей других регионов.
Заключение
55