- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема урока: Сдвиг графика функции у = ах? вдоль осей координат. презентация
Содержание
- 1. Тема урока: Сдвиг графика функции у = ах? вдоль осей координат.
- 2. 1. Что произошло с графиком функции
- 3. у х 0 1 1
- 4. у 1 1 0 х
- 5. График функции у = ах²+ ?
- 6. 1. Что представляет собой функция у =
- 7. у 1 1 0 х
- 8. у 1 0 1 х
- 9. у 1 1 0 х
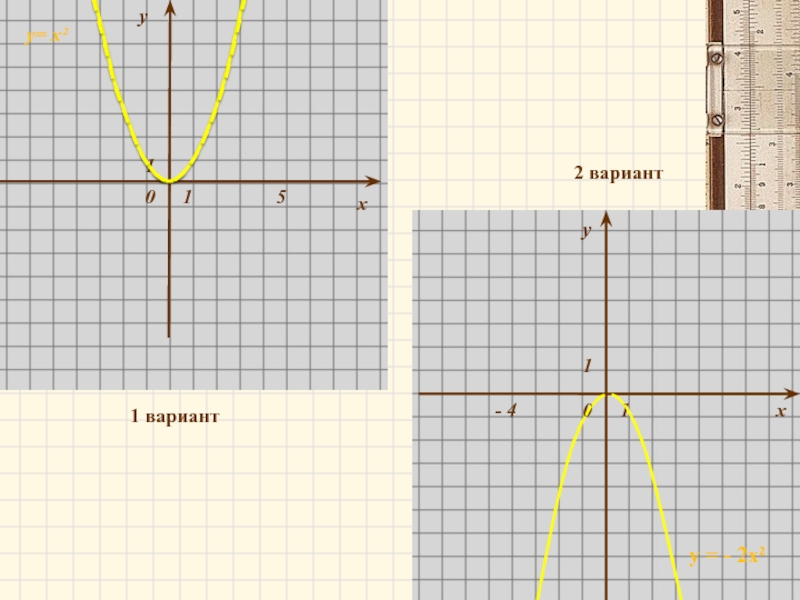
- 10. Вариант 1. а) б) а) в)
- 11. График функции у = ах²+ ? сдвиг
- 12. Задайте формулой параболу, изображённую на рисунке:
- 13. Контрольный тест В.1 1 ур. 1. 1)
Слайд 21. Что произошло с графиком функции у = ах2?
2. На сколько единиц сдвинулся график?
3. Изменились значения аргумента или функции?
4. Сравните значение функции исходной параболы со значением
функции получившейся параболы
5. Запишите формулу получившейся параболы
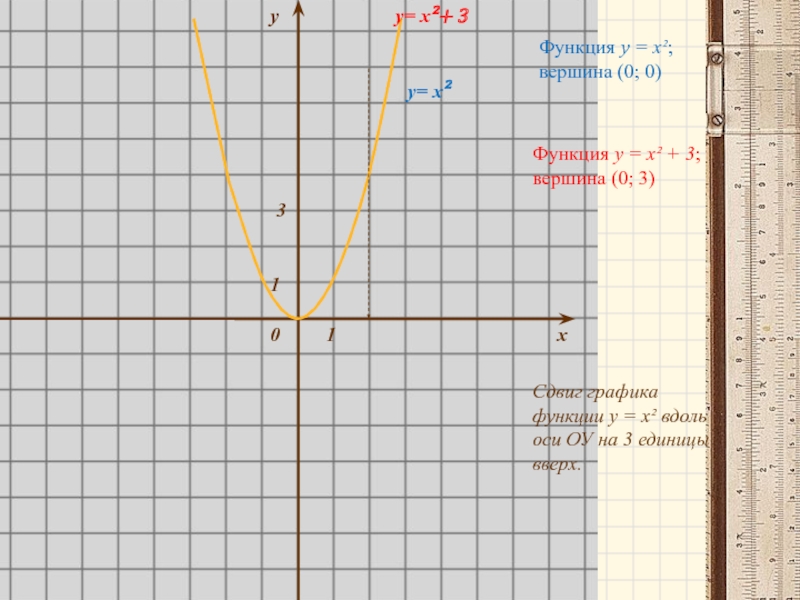
Слайд 3у
х
0
1
1
3
у= х²
у= х²+ 3
Функция у = х²; вершина (0; 0)
Функция у
Сдвиг графика функции у = х² вдоль оси ОУ на 3 единицы вверх.
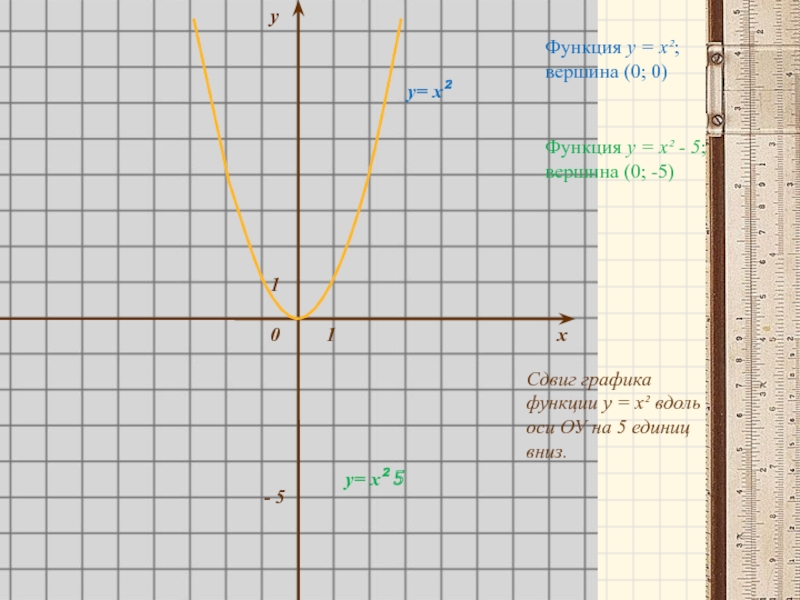
Слайд 4у
1
1
0
х
- 5
у= х²
у= х² 5
Функция у = х²; вершина (0; 0)
Функция
Сдвиг графика функции у = х² вдоль оси ОУ на 5 единиц вниз.
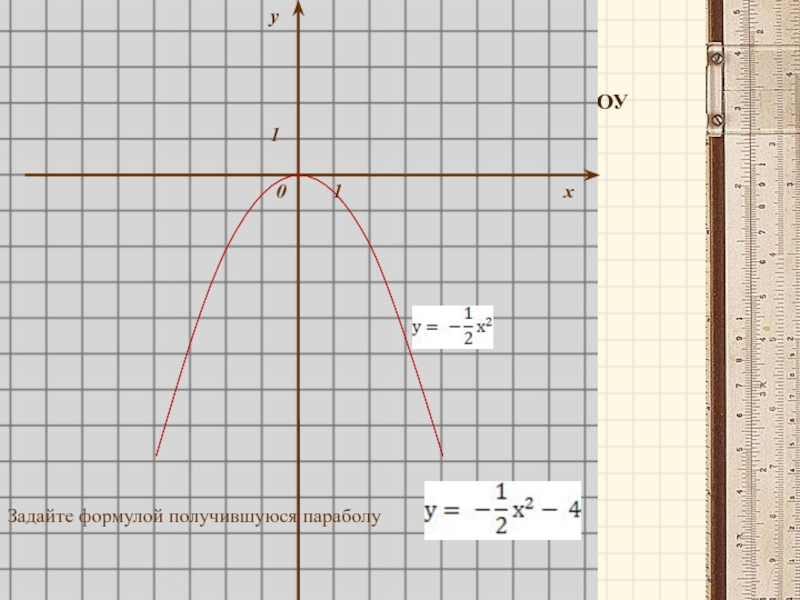
Слайд 5График функции у = ах²+ ?
сдвиг графика функции у =
если ? > 0, то вверх на ? единиц
если ? < 0, то вниз на ⃒ ?⃒ единиц
Вершина параболы в точке (0; ?)
у
1
0
1
х
Задайте формулой получившуюся параболу
Слайд 61. Что представляет собой функция у = а( х + р)
2. Составьте алгоритм получения графика
функции у = а( х + р) 2 из параболы у = ах2
3. Где находится вершина параболы у = а( х + р) 2?
График функции у = а(х + р) ²
сдвиг графика функции у = ах² вдоль оси ОХ
если р > 0, то влево на р единиц
Если р < 0, то вправо на ⃒ р ⃒ единиц
Вершина параболы в точке ( - р; 0)
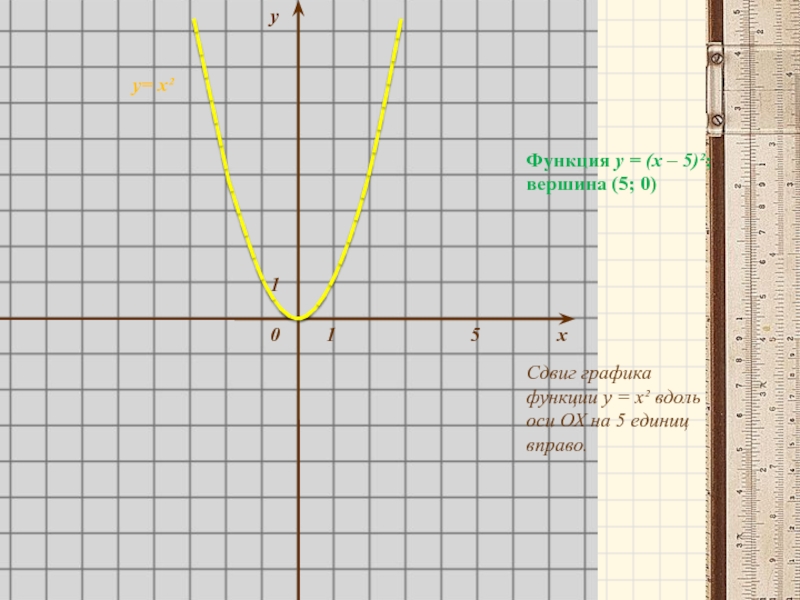
Слайд 7у
1
1
0
х
5
у= х²
Функция у = (х – 5)²; вершина (5; 0)
Сдвиг графика
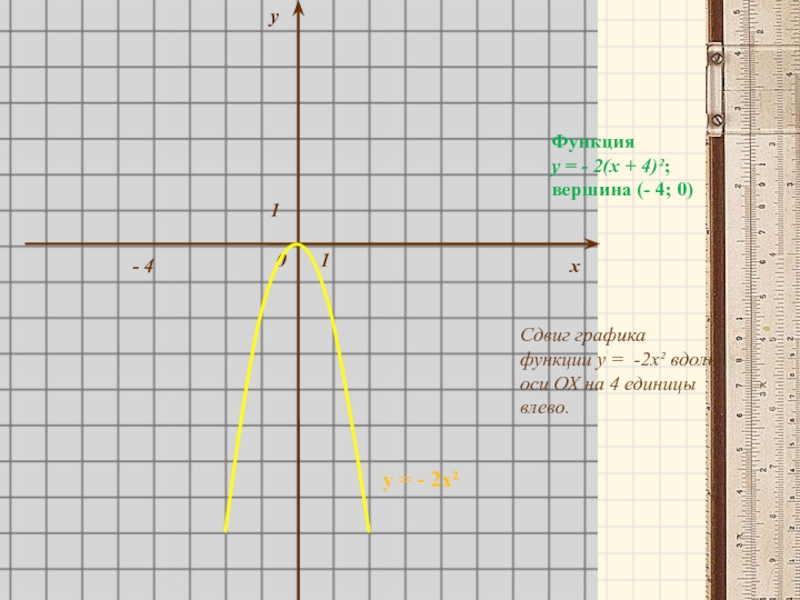
Слайд 8у
1
0
1
х
у = - 2х²
- 4
Функция
у = - 2(х + 4)²;
вершина (- 4; 0)
Сдвиг графика функции у = -2х² вдоль оси ОХ на 4 единицы влево.
Слайд 11График функции у = ах²+ ?
сдвиг графика функции у = ах²
если ? > 0, то вверх на ? единиц
если ? < 0, то вниз на ⃒ ?⃒ единиц
Вершина параболы в точке (0; ?)
График функции у = а(х + р) ²
сдвиг графика функции у = ах² вдоль оси ОХ
если р > 0, то влево на ⃒ р ⃒ единиц
Если р < 0, то вправо на р единиц
Вершина параболы в точке (- р; 0)
у = 3х² + 7
у = 2х
у = - 0,5х² - 2
у = (х – 6)²
у = - 7(х + 1)²
На рисунке изображены графики функций
вида у = ах²+ ?.
В каждом случае укажите
знаки коэффициентов а и ?
у = 3х² + 7, вверх, (0; 7)
у = - 0,5х² - 2 , вниз, (0; -2)
2. у = (х – 6)², вверх, (6; 0)
у = - 7(х + 1)², вниз, (-1; 0)
а) а >0, ? > 0
б) а < 0, ? > 0
в) а >0, ? < 0
г) а < 0, ? < 0
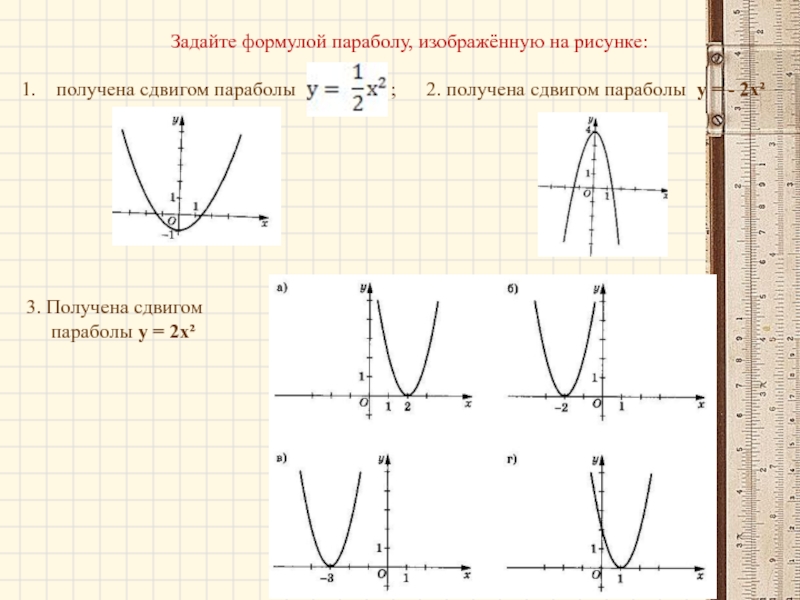
Слайд 12Задайте формулой параболу, изображённую на рисунке:
получена сдвигом параболы
3. Получена сдвигом
параболы у = 2х²
Слайд 13Контрольный тест
В.1
1 ур.
1. 1) да
2) да
3) нет
2. 1) да
2)нет
3) да
4) нет
3. 1) б
2) г
3) в
4) а
2 ур.
1. ОУ, q>0, q<0
2. у = -2(х +4)2
3. 2,4.
В.2
1 ур.
1. 1) да
2) нет
3) да
4) нет
2. 1) да
2)да
3) нет
4) нет
3. а) 1,3
б) 2,4
2 ур.
1.
2. х = ± 2
3. а = 3
В.3
1 ур.
1. а) 2, 3, 5
б) 1, 4
2.
3. 1) да
2) нет
3) нет
4) да
2 ур.
1. ОХ, р>0, р<0
2. у = -(х +4)2
3. 1,4.
В.4
1 ур.
1. а) 1, 3
б) 2, 5
2. 1) б
2) г
3) в
4) а
3. 1) нет
2) да
3) да
4) нет
2 ур.
1. у = -2х2 – 2
2. 1) да
2) да
3) нет
4) нет
3.
Е(у): ( - ∞; -1,2]
М
О
Л
О
Д
Ц
Ы !