№231», г. Знаменск, Астраханской области.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема урока: Метод интервалов презентация
Содержание
- 1. Тема урока: Метод интервалов
- 2. В математике есть своя красота, как в живописи и в поэзии. В.А.Жуковский
- 3. , , Ребус Н, ,,,А ,,,Н ,,
- 4. Решение неравенств методом интервалов. Цель урока: Продолжить
- 5. Викторина Как называется выражение, содержащее знак «>» или «
- 6. Алгоритм решения неравенств методом интервалов 1. Ввести
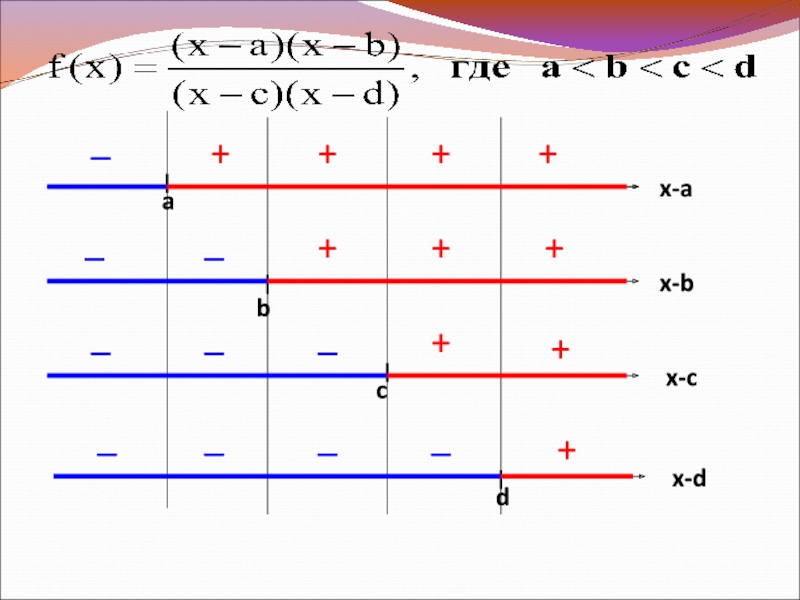
- 8. a b c d x-d x-c x-b
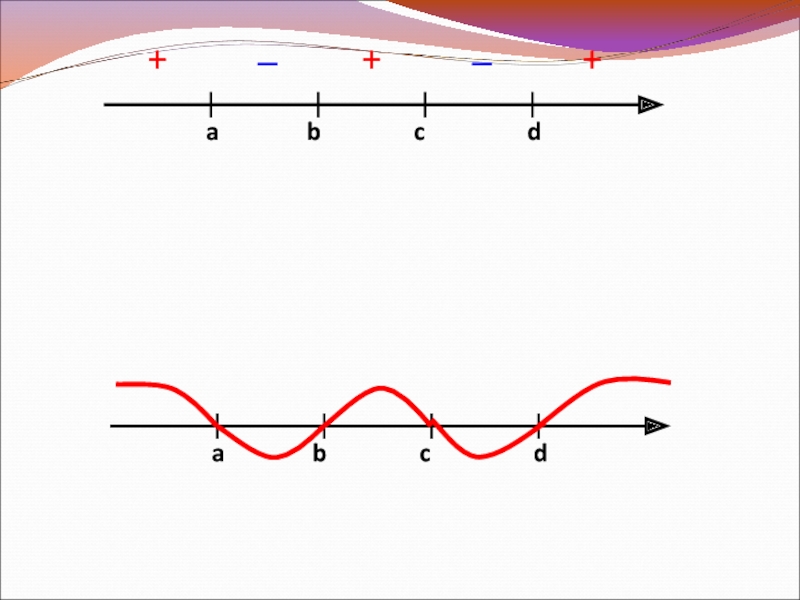
- 9. a b c d _ + +
- 10. Свойства Свойство правого крайнего знака. Необходимо, преобразовать
- 11. Итог урока Решение неравенств: используя свойства метода
Слайд 1Тема урока:
«Метод интервалов»
Подготовила: Чикишева Елена Викторовна, учитель математики МОУ «Гимназия
Слайд 4Решение неравенств методом интервалов.
Цель урока:
Продолжить формирование знаний и умений решения неравенств
методом интервалов.
Задачи:
Закрепить умения решения различных видов неравенств методом интервалов.
Развивать умения сравнивать решения, выявлять правильные ответы.
- Развивать умения сравнивать решения, выявлять правильные ответы.
- Развивать у учащихся познавательный интерес к предмету, сообразительность, любознательность, логическое мышление, укреплять память учащихся.
- Вовлечь учащихся в активную практическую деятельность.
Воспитывать аккуратность при оформлении решений, умение преодолевать трудности при решении неравенств.
Задачи:
Закрепить умения решения различных видов неравенств методом интервалов.
Развивать умения сравнивать решения, выявлять правильные ответы.
- Развивать умения сравнивать решения, выявлять правильные ответы.
- Развивать у учащихся познавательный интерес к предмету, сообразительность, любознательность, логическое мышление, укреплять память учащихся.
- Вовлечь учащихся в активную практическую деятельность.
Воспитывать аккуратность при оформлении решений, умение преодолевать трудности при решении неравенств.
Слайд 5Викторина
Как называется выражение, содержащее знак «>» или «
вы знаете?
Что означают промежутки знакопостоянства на координатной плоскости?
Что означают промежутки знакопостоянства на координатной плоскости?
Слайд 6Алгоритм решения неравенств методом интервалов
1. Ввести функцию и найти её область
определения.
2. Сравнить функцию с нулём.
3. Приравнять функцию к нулю. (Найти нули функции).
4. Начертить ось абсцисс и расставить на ней нули функции, в порядке возрастания. Выделить интервалы.
5. Определить знаки функции, на промежутках знакопостоянства, с помощью вычислений.
6. Заштриховать верные промежутки и выписать их.
7. Записать ответ.
2. Сравнить функцию с нулём.
3. Приравнять функцию к нулю. (Найти нули функции).
4. Начертить ось абсцисс и расставить на ней нули функции, в порядке возрастания. Выделить интервалы.
5. Определить знаки функции, на промежутках знакопостоянства, с помощью вычислений.
6. Заштриховать верные промежутки и выписать их.
7. Записать ответ.
Слайд 10Свойства
Свойство правого крайнего знака.
Необходимо, преобразовать неравенство так чтобы во всех множителях(или
в числителе и знаменателе), слагаемое с переменной стояло на первом месте. Тогда правый крайний интервал всегда будет положительным.
Свойство множителей с чётными степенями.
Если в неравенстве есть множители с чётными степенями, то относительно их нулей функции знаки «+» и «-»не чередуются.
Свойство множителей с чётными степенями.
Если в неравенстве есть множители с чётными степенями, то относительно их нулей функции знаки «+» и «-»не чередуются.
Слайд 11Итог урока
Решение неравенств:
используя свойства метода интервалов;
с помощью перенесения слагаемых;
с помощью
разложения на множители;
с выполнением дополнительных условий.
с выполнением дополнительных условий.