- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема урока: презентация
Содержание
- 1. Тема урока:
- 2. I. Cумма углов треугольника 1. На доске
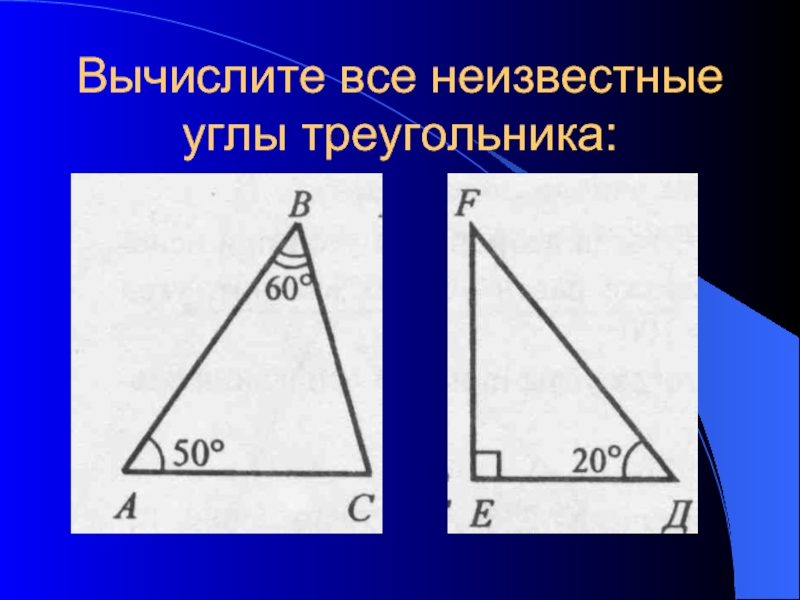
- 3. Вычислите все неизвестные углы треугольника:
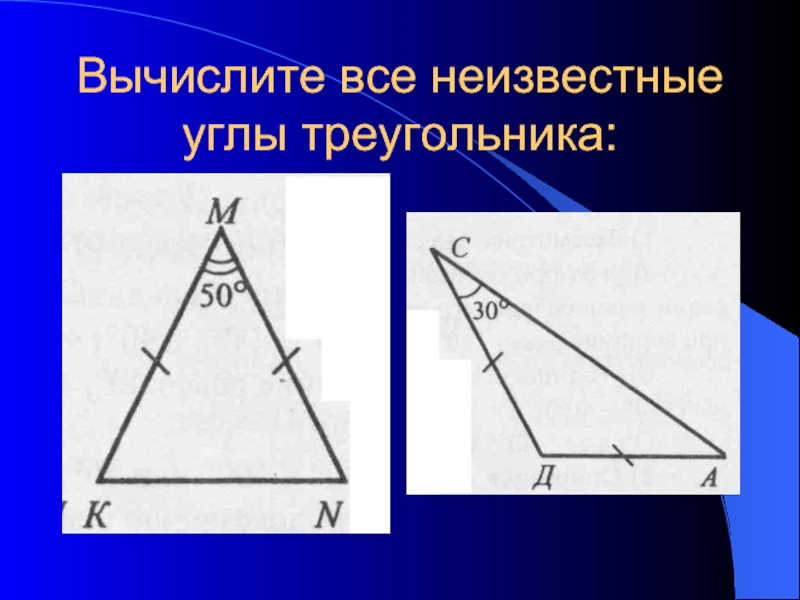
- 4. Вычислите все неизвестные углы треугольника:
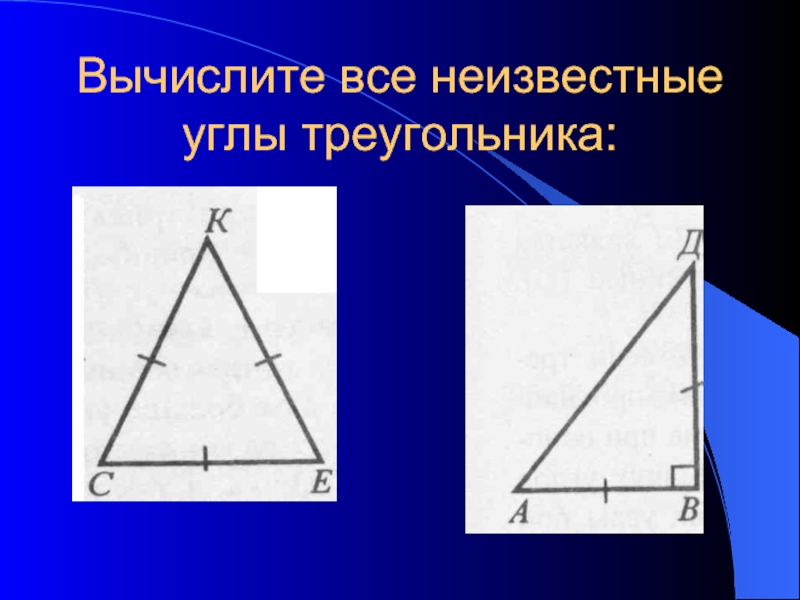
- 5. Вычислите все неизвестные углы треугольника:
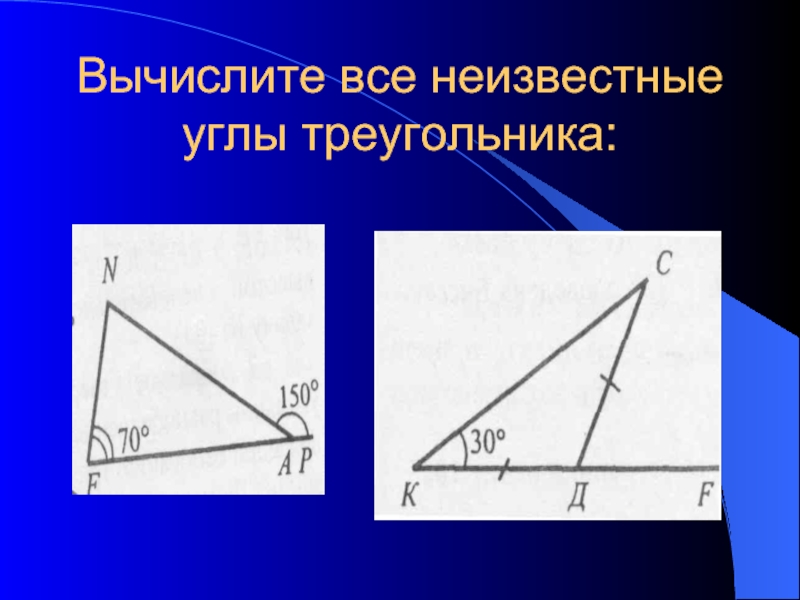
- 6. Вычислите все неизвестные углы треугольника:
- 7. II. Изучение нового материла Внешним
- 8. Докажем теорему: Внешний угол треугольника
- 9. Условие теоремы: Дано: треугольник, ∠4
- 10. Доказательство: ∠4 – внешний угол,
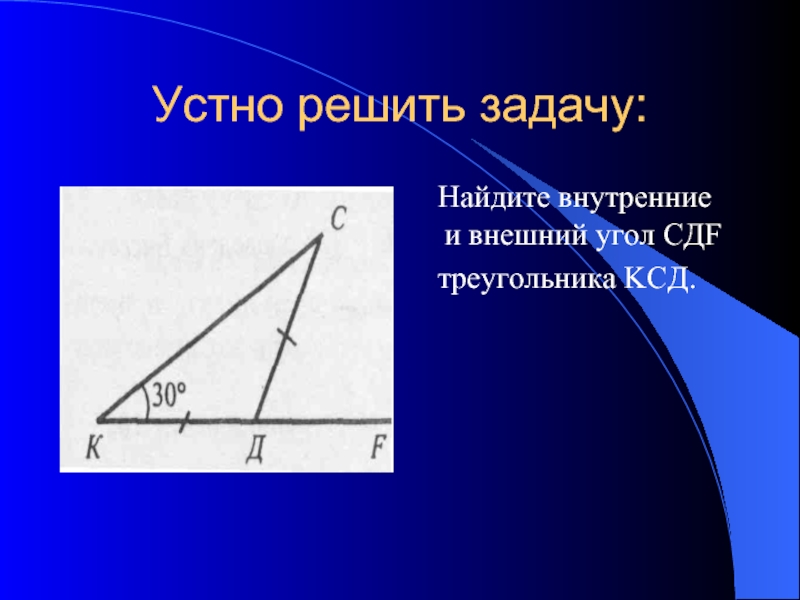
- 11. Устно решить задачу: Найдите
- 12. Решение задач Решить задачу . Дано:
- 13. Решение Проведем биссектрисы BF
- 14. IV.Самостоятельная работа Вариант I 1. Один из
Слайд 2I. Cумма углов треугольника
1. На доске доказать теорему о сумме углов
треугольника:
Сумма углов треугольника равна 1800
2. Решить задачу № 749 (чёт 1в., нечёт 2в.)
3. Решить устно:
Сумма углов треугольника равна 1800
2. Решить задачу № 749 (чёт 1в., нечёт 2в.)
3. Решить устно:
Слайд 7II. Изучение нового материла
Внешним углом треугольника называется угол, смежный
с каким- нибудь углом этого треугольника
На рис. ∠4- внешний
На рис. ∠4- внешний
Слайд 8Докажем теорему:
Внешний угол треугольника равен сумме двух углов треугольника,
не смежных с ним.
Слайд 10Доказательство:
∠4 – внешний угол, смежный с ∠3 данного треугольника.
Так как ∠ 4+∠ 3=1800 , а по теореме о сумме углов треугольника
(∠ 1+∠ 2)+ ∠ 3=1800 ,
то ∠ 4=∠ 1+∠ 2,
что и требовалось доказать.
(∠ 1+∠ 2)+ ∠ 3=1800 ,
то ∠ 4=∠ 1+∠ 2,
что и требовалось доказать.
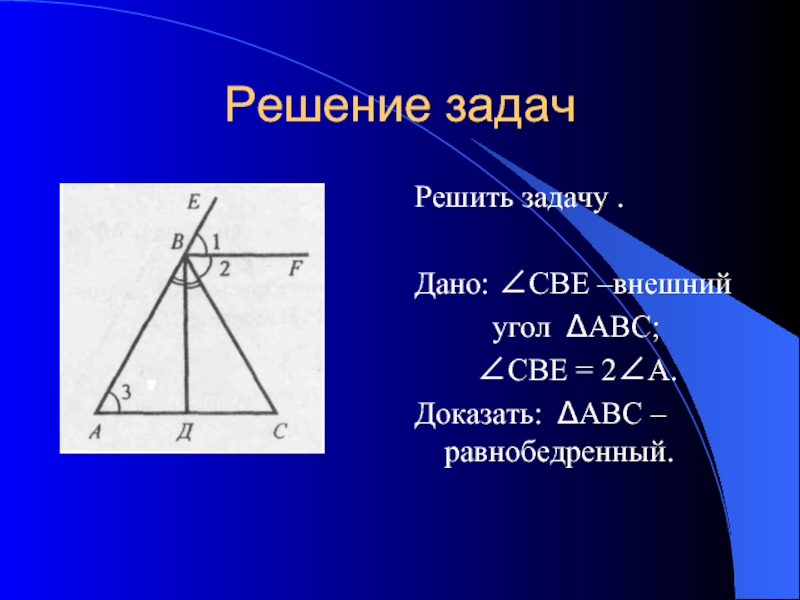
Слайд 12Решение задач
Решить задачу .
Дано: ∠СВЕ –внешний
угол ΔАВС;
∠СВЕ = 2∠А.
Доказать: ΔАВС – равнобедренный.
∠СВЕ = 2∠А.
Доказать: ΔАВС – равнобедренный.
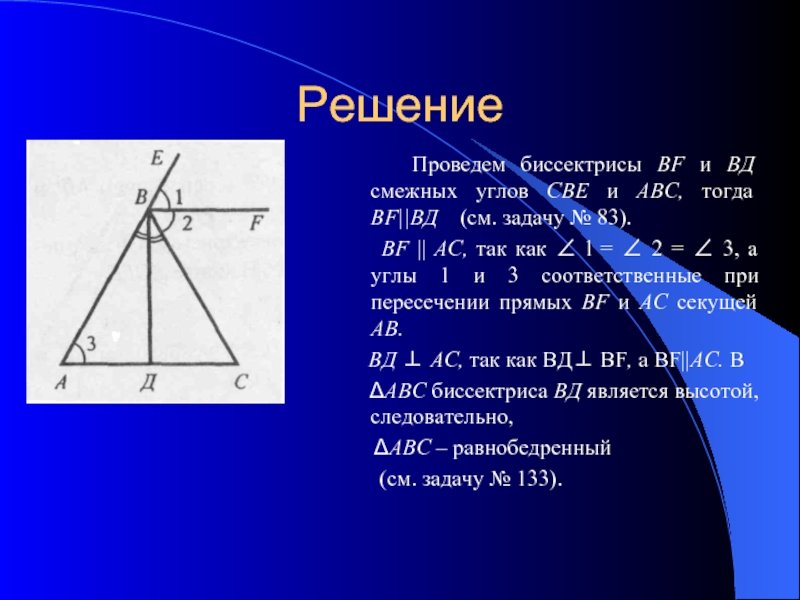
Слайд 13Решение
Проведем биссектрисы BF и ВД смежных углов СВЕ
и ABC, тогда ВF||ВД (см. задачу № 83).
BF || АС, так как ∠ l = ∠ 2 = ∠ 3, а углы 1 и 3 соответственные при пересечении прямых BF и АС секущей АВ.
ВД ⊥ АС, так как BД⊥ BF, a BF||AC. В
ΔABC биссектриса ВД является высотой, следовательно,
ΔABC – равнобедренный
(см. задачу № 133).
BF || АС, так как ∠ l = ∠ 2 = ∠ 3, а углы 1 и 3 соответственные при пересечении прямых BF и АС секущей АВ.
ВД ⊥ АС, так как BД⊥ BF, a BF||AC. В
ΔABC биссектриса ВД является высотой, следовательно,
ΔABC – равнобедренный
(см. задачу № 133).
Слайд 14IV.Самостоятельная работа
Вариант I
1. Один из углов равнобедренного треугольника равен 96°.
Найдите два других угла треугольника.
2. В треугольнике СДЕ с углом ∠ E = 32° проведена биссектриса CF,
∠ СЕД =72°. Найдите ∠Д.
Вариант II
1. Один из углов равнобедренного треугольника равен 108°. Найдите два других угла треугольника.
2. В треугольнике СДЕ проведена биссектриса CF, ∠ Д = 68°, ∠E =32°. Найдите ∠СFД.
Вариант III
1. В равнобедренном треугольнике MNP с основанием МР и углом ∠N = 64° проведена высота МН. Найдите ∠РМН.
2. В треугольнике СДЕ проведены биссектрисы СК и ДР,
пересекающиеся в точке F, причем ∠ ДРК = 78°. Найдите ∠ СЕД.
2. В треугольнике СДЕ с углом ∠ E = 32° проведена биссектриса CF,
∠ СЕД =72°. Найдите ∠Д.
Вариант II
1. Один из углов равнобедренного треугольника равен 108°. Найдите два других угла треугольника.
2. В треугольнике СДЕ проведена биссектриса CF, ∠ Д = 68°, ∠E =32°. Найдите ∠СFД.
Вариант III
1. В равнобедренном треугольнике MNP с основанием МР и углом ∠N = 64° проведена высота МН. Найдите ∠РМН.
2. В треугольнике СДЕ проведены биссектрисы СК и ДР,
пересекающиеся в точке F, причем ∠ ДРК = 78°. Найдите ∠ СЕД.