- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 5. Законы сохранения в нерелятивистской механике.Система материальных точек презентация
Содержание
- 1. Тема 5. Законы сохранения в нерелятивистской механике.Система материальных точек
- 2. Консервативными
- 3. y x A = mgּh
- 4. α A = mglcosα = mg(h1
- 5. Работа консервативной силы A1a2 = A1b2
- 6. 5.2. Примеры консервативных сил
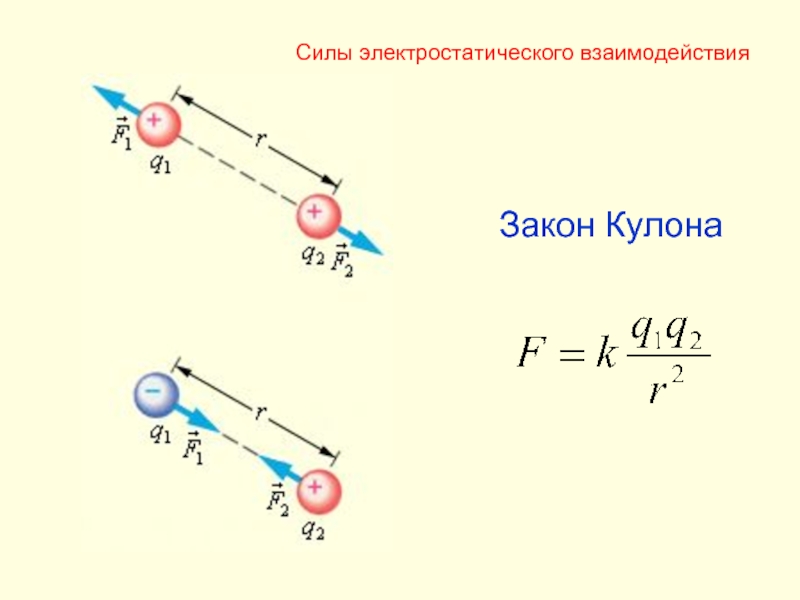
- 7. Закон Кулона Силы электростатического взаимодействия
- 8. Q q
- 9. Q q
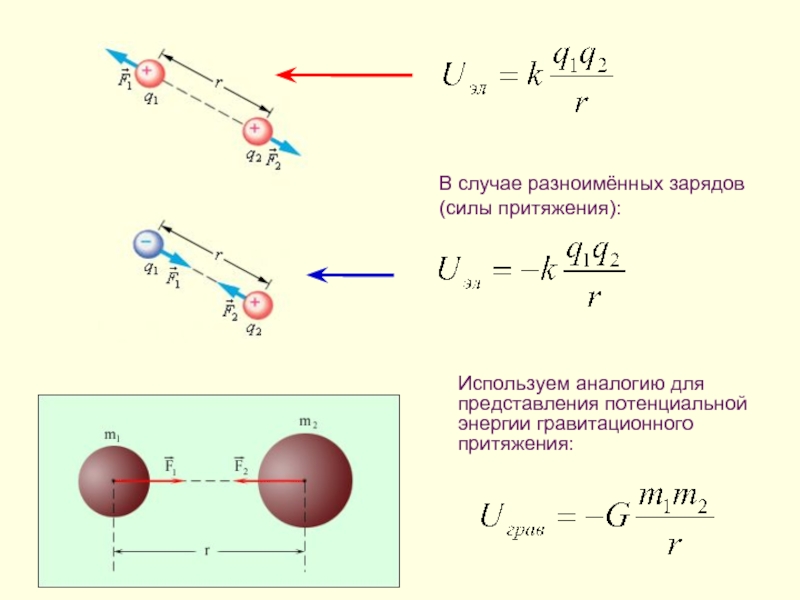
- 10. В случае разноимённых зарядов (силы притяжения): Используем аналогию для представления потенциальной энергии гравитационного притяжения:
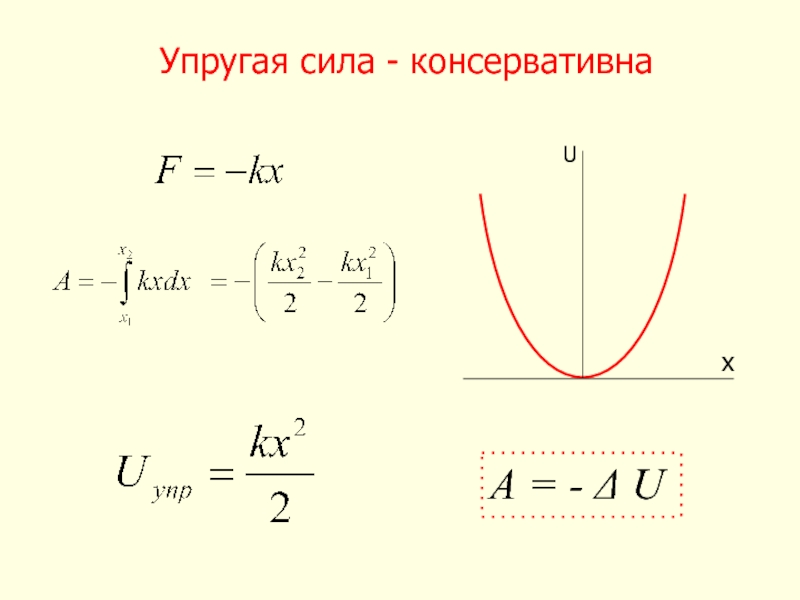
- 11. Упругая сила - консервативна A = - Δ U x U
- 12. 5.3. Сохранение механической энергии
- 13. Для одной частицы в поле потенциальных сил
- 14. 5.4. Система материальных точек.
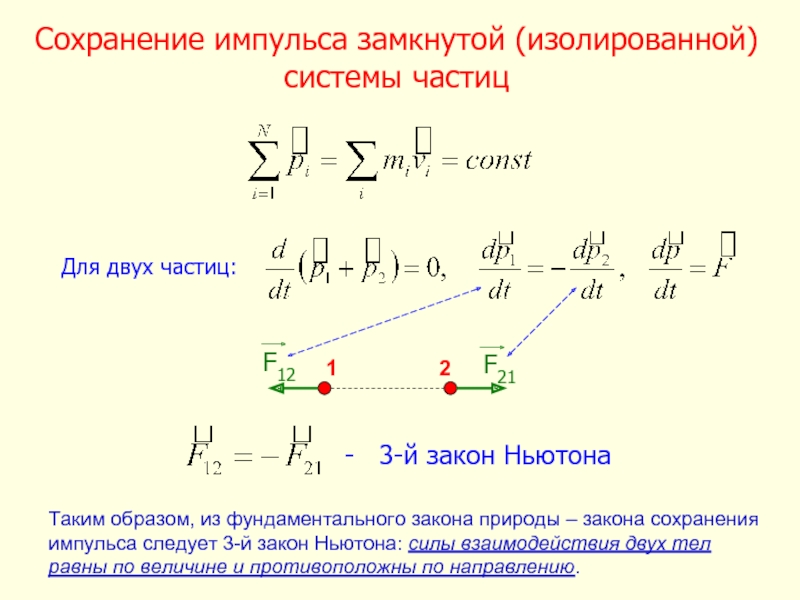
- 15. Сохранение импульса замкнутой (изолированной) системы частиц Для
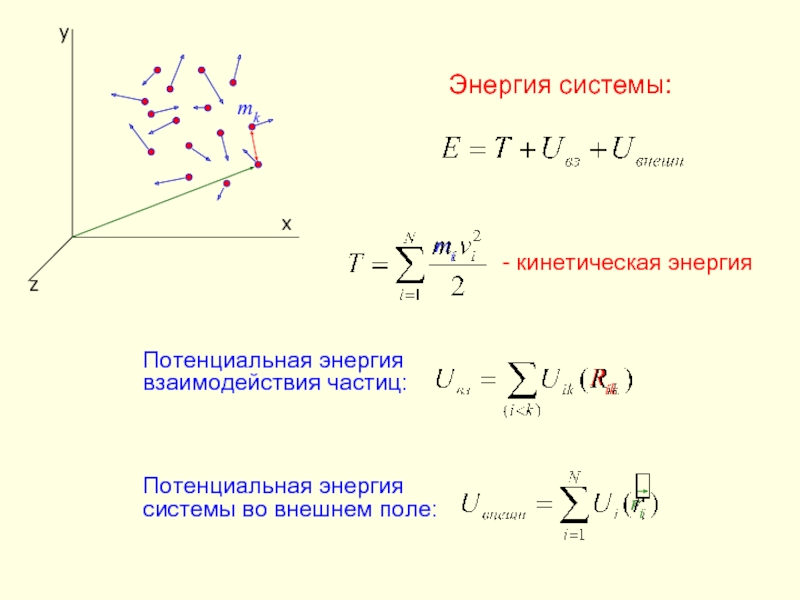
- 16. y x z Rik mi Энергия системы:
- 17. y x z Rik mi Закон сохранения
- 18. 5.5. Центр масс системы частиц.
- 19. y x z с с –
- 20. Центр масс системы из 2-х материальных точек
- 21. 5.6. Уравнение движения центра масс системы частиц
- 22. y x z с 0 -
- 23. Для замкнутой (изолированной) системы частиц:
- 24. - уравнение движения центра масс системы частиц
- 25. 1. Лампочка не в центре масс
- 26. 2. Лампочка в центре масс
- 27. 2. Лампочка в центре масс
- 28. 2. Лампочка в центре масс
- 29. 1. Лампочка не в центре масс
- 30. Конец темы
Слайд 1Тема 5. Законы сохранения в нерелятивистской механике.
Система материальных точек
5.1. Консервативные силы.
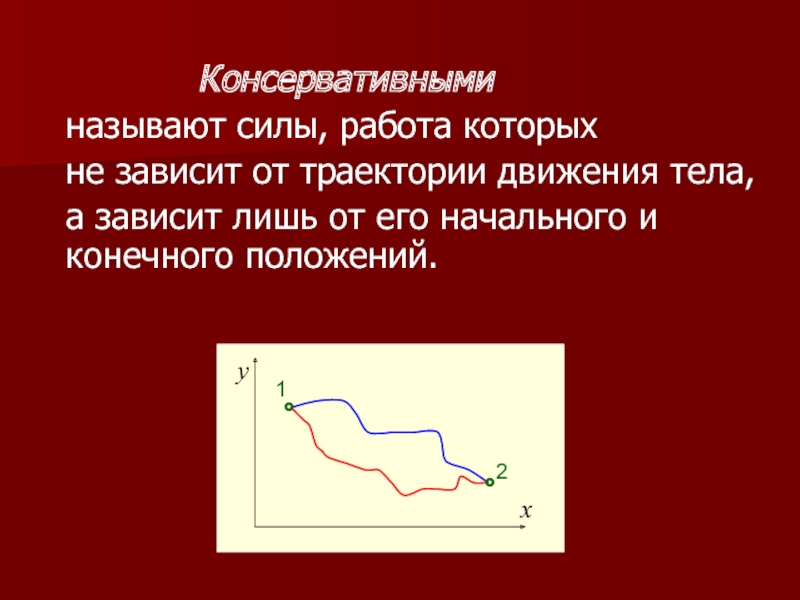
Слайд 2 Консервативными
называют силы, работа которых
не зависит от траектории движения тела,
а зависит лишь от его начального и конечного положений.
x
y
1
2
Слайд 3y
x
A = mgּh = mgh cosα = mgh.
U
A = - Δ U
Рассмотрим работу силы тяжести на участке траектории от h1 до h2 .
Если считать силу тяжести постоянной и все время совпадающей по направлению с вектором перемещения, то:
Но по модулю h = h1 – h2 ,
т.е. A = mg(h1 - h2) =
= - (mgh2 – mgh1)= - ΔU,
Таким образом, работа в данном случае определяется разностью начального и конечного значений некоторой функции, зависящей от высоты положения тела. Эта функция называется потенциальной энергией:
Работа же равна убыванию потенциальной энергии (этим объясняется знак минус):
Слайд 4
α
A = mglcosα = mg(h1 - h2) =
= - (mgh2 -
U = mgh
1
2
y
dy
Покажем, что сила тяжести является консервативной.
Пусть тело перемещается под действием силы тяжести по двум разным траекториям, но начальные и конечные точки этих траекторий совпадают.
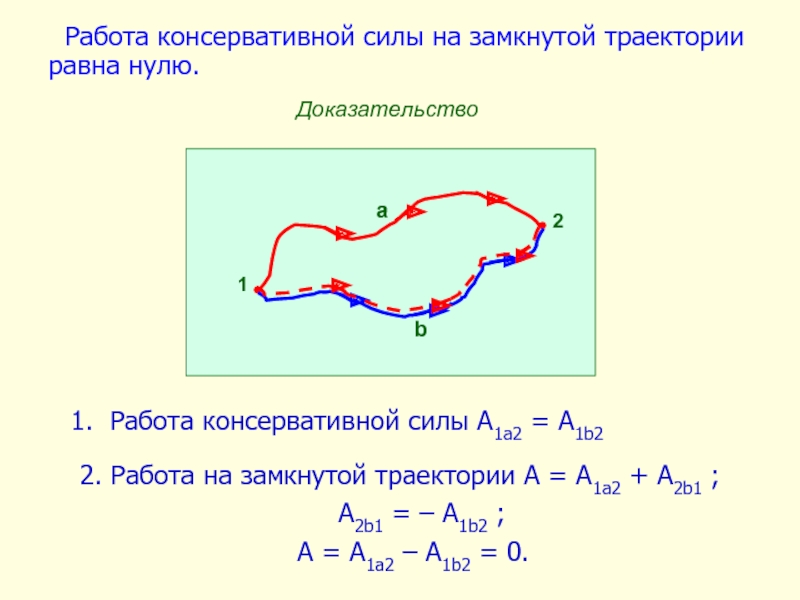
Слайд 5Работа консервативной силы A1a2 = A1b2
2. Работа на замкнутой траектории
A2b1 = – A1b2 ;
А = A1a2 – A1b2 = 0.
Работа консервативной силы на замкнутой траектории равна нулю.
1
2
b
a
Доказательство
Слайд 65.2. Примеры консервативных сил
Тема 5. Законы сохранения
Слайд 8
Q
q
1
2
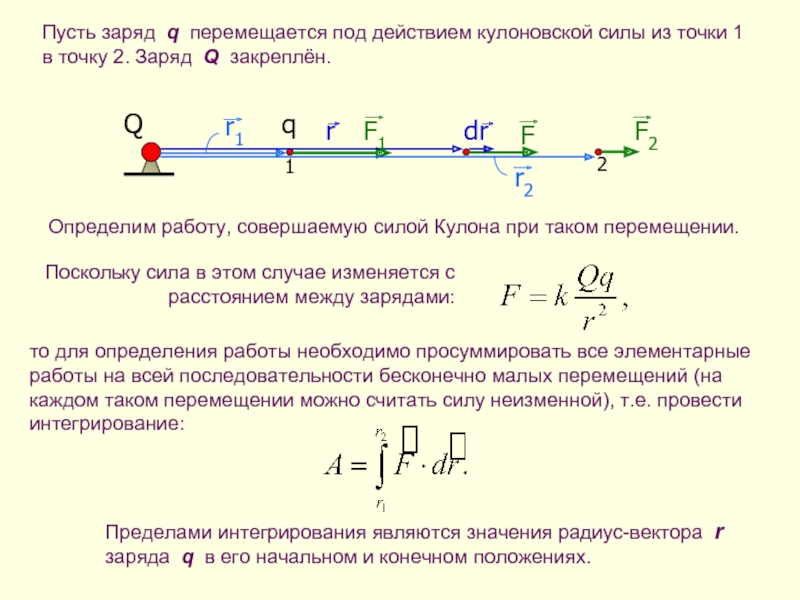
Пусть заряд q перемещается под действием кулоновской силы из точки 1
Поскольку сила в этом случае изменяется с расстоянием между зарядами:
то для определения работы необходимо просуммировать все элементарные работы на всей последовательности бесконечно малых перемещений (на каждом таком перемещении можно считать силу неизменной), т.е. провести интегрирование:
Пределами интегрирования являются значения радиус-вектора r заряда q в его начальном и конечном положениях.
Определим работу, совершаемую силой Кулона при таком перемещении.
Слайд 9
Q
q
1
2
A = - Δ U
Из результата интегрирования видно, что и в
Слайд 10В случае разноимённых зарядов (силы притяжения):
Используем аналогию для представления потенциальной энергии
Слайд 125.3. Сохранение
механической энергии частицы
в поле
Тема 5. Законы сохранения в нерелятивистской механике.
Система материальных точек
Слайд 13Для одной частицы в поле потенциальных сил
В поле сил тяжести
у
Работа, определяемая убывание потенциальной энергии U,
идёт на приращение кинетической энергии тела Т :
т.е.
откуда:
Следовательно:
Таким образом, механическая энергия частицы
в поле потенциальных сил со временем не меняется:
Слайд 145.4. Система материальных точек.
Сохранение механической энергии и импульса
Тема 5. Законы сохранения в нерелятивистской механике.
Система материальных точек
Слайд 15Сохранение импульса замкнутой (изолированной) системы частиц
Для двух частиц:
- 3-й закон
1
2
Таким образом, из фундаментального закона природы – закона сохранения импульса следует 3-й закон Ньютона: силы взаимодействия двух тел
равны по величине и противоположны по направлению.
Слайд 16y
x
z
Rik
mi
Энергия системы:
- кинетическая энергия
Потенциальная энергия взаимодействия частиц:
Потенциальная энергия системы во внешнем
mk
Слайд 17y
x
z
Rik
mi
Закон сохранения механической энергии: полная механическая энергия системы тел, на которые
mk
Для замкнутой системы тел, взаимодействующих консервативными силами:
При действии неконсервативных сил (как внешних, так и внутренних):
Слайд 185.5. Центр масс системы частиц.
Скорость центра
Тема 5. Законы сохранения в нерелятивистской механике.
Система материальных точек
Слайд 19y
x
z
с
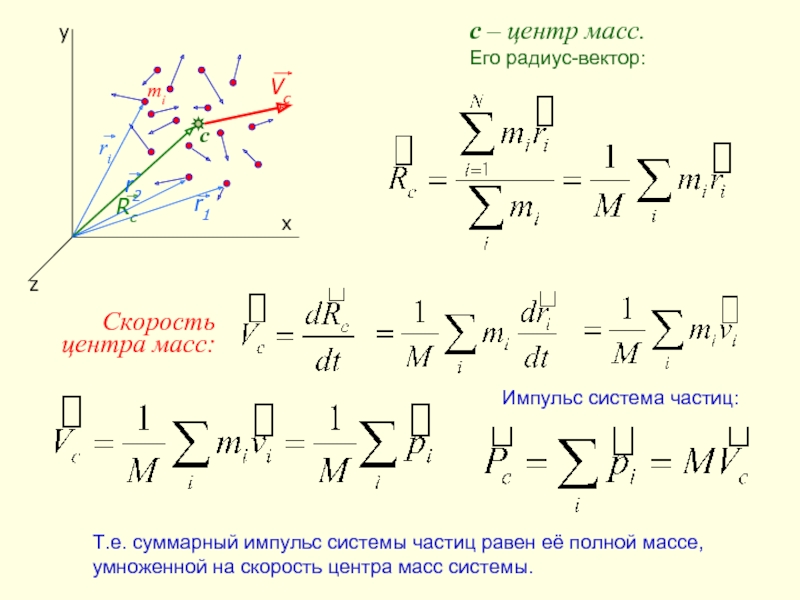
с – центр масс.
Его радиус-вектор:
Скорость центра масс:
mi
Импульс система частиц:
Т.е. суммарный
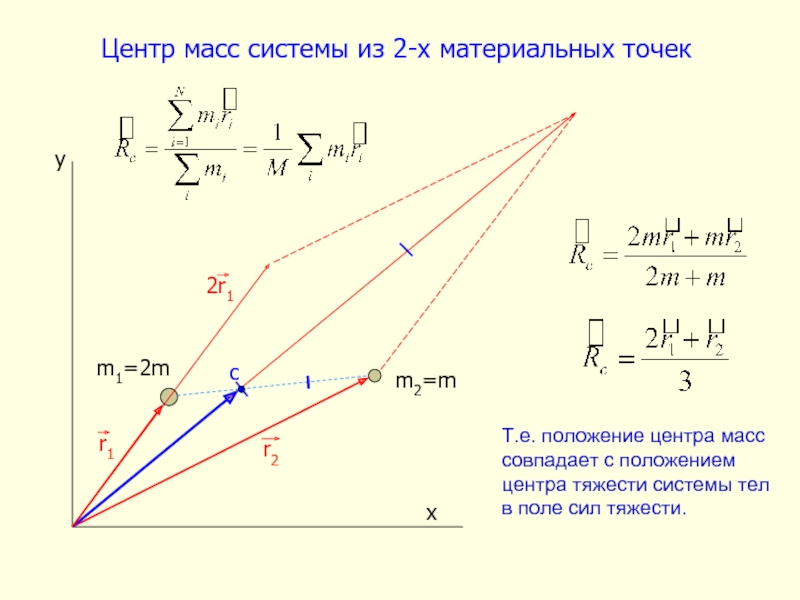
Слайд 20Центр масс системы из 2-х материальных точек
с
y
x
m1=2m
m2=m
Т.е. положение центра масс совпадает
Слайд 215.6. Уравнение движения центра масс системы частиц
Тема 5. Законы сохранения в
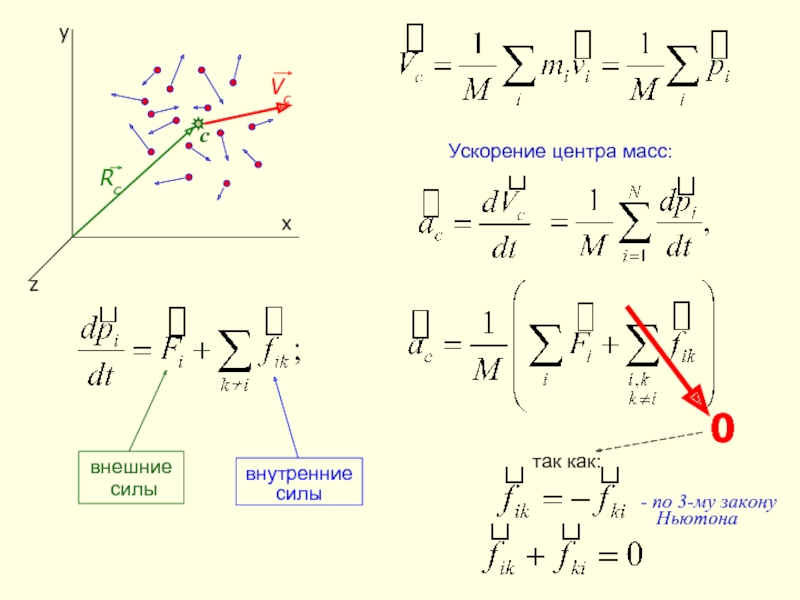
Слайд 23Для замкнутой (изолированной) системы частиц:
- уравнение движения центра масс системы частиц
Следовательно,
т.е. силы со стороны тел, не принадлежащих данной системе.
Таким образом, что бы не происходило внутри замкнутой системы, её центр масс движется равномерно прямолинейно (или покоится).