- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тела вращения презентация
Содержание
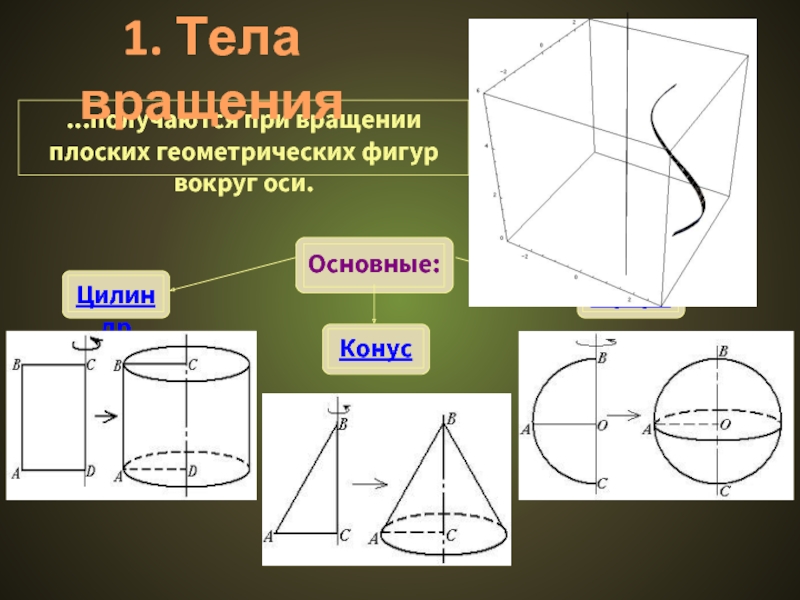
- 1. Тела вращения
- 2. ...получаются при вращении плоских геометрических фигур вокруг оси. 1. Тела вращения
- 3. Отрезок ОО1 — высота. ВВ1С1С — осевое
- 4. Отрезок ОS — высота. AВS — осевое
- 5. Осевое сечение — круг радиусом R.
- 6. Задачка для маляра: сколько краски необходимо, чтобы
- 7. 6. Тест В тетради пронумеруйте 12 вопросов
- 8. При вращении каких фигур вокруг указанных осей
- 9. Укажите ось, при вращении вокруг которой данной
- 10. Какие фигуры при вращении вокруг указанной оси
- 11. Какие поверхности получаются при вращении данной фигуры
- 12. Образующей прямого кругового цилиндра, приведенного на рисунке,
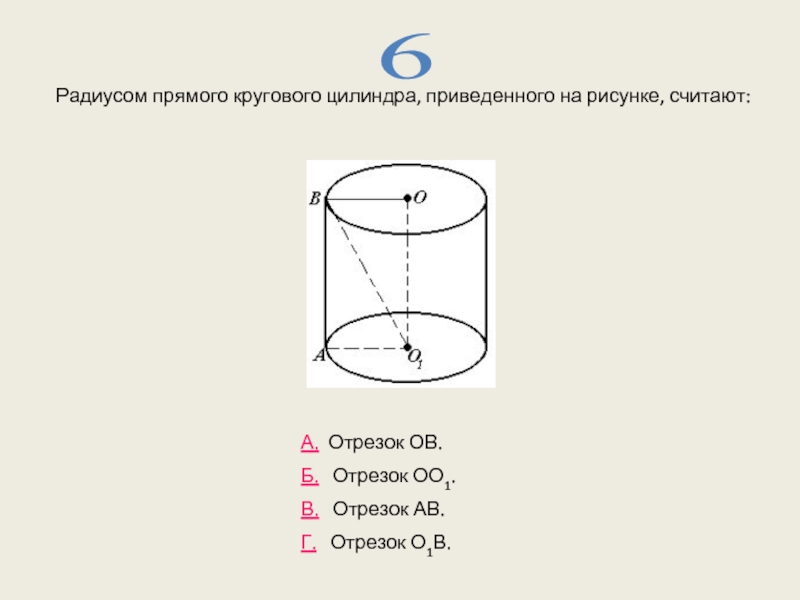
- 13. Радиусом прямого кругового цилиндра, приведенного на рисунке,
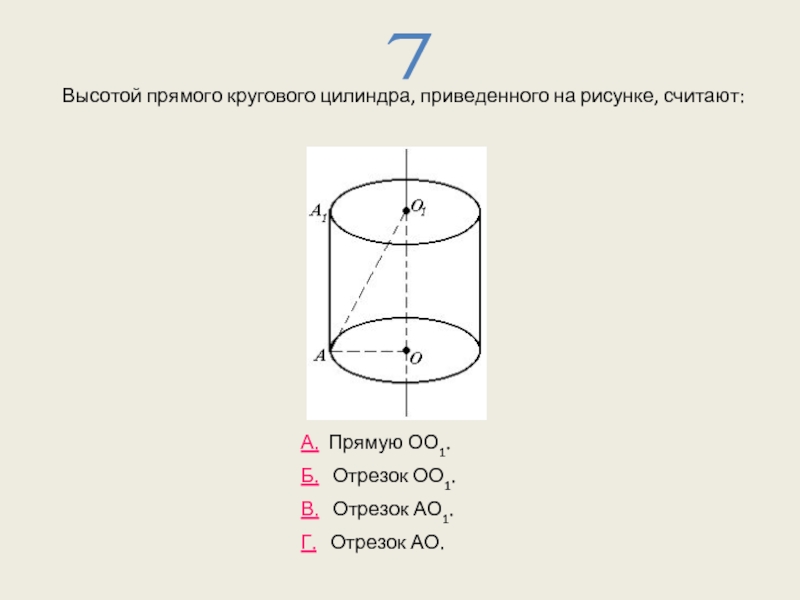
- 14. Высотой прямого кругового цилиндра, приведенного на рисунке,
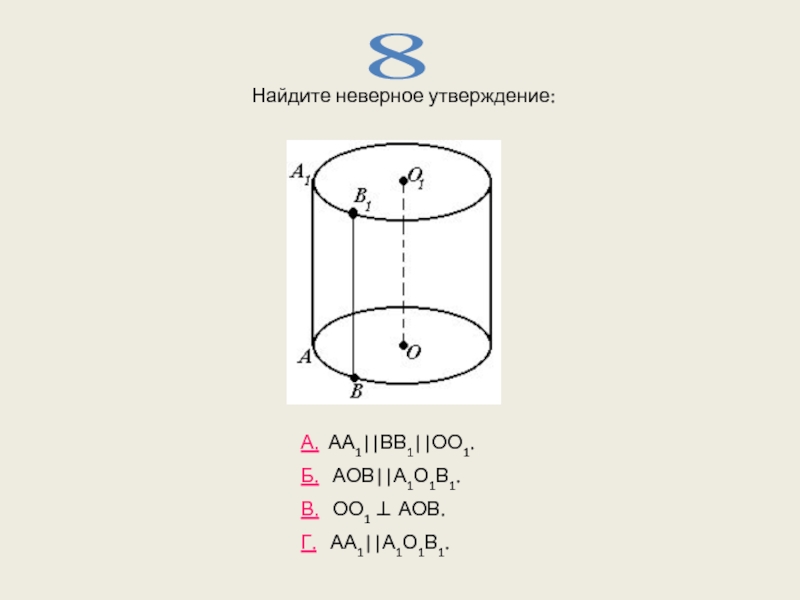
- 15. Найдите неверное утверждение: 8 А. АА1||ВВ1||ОО1. Б.
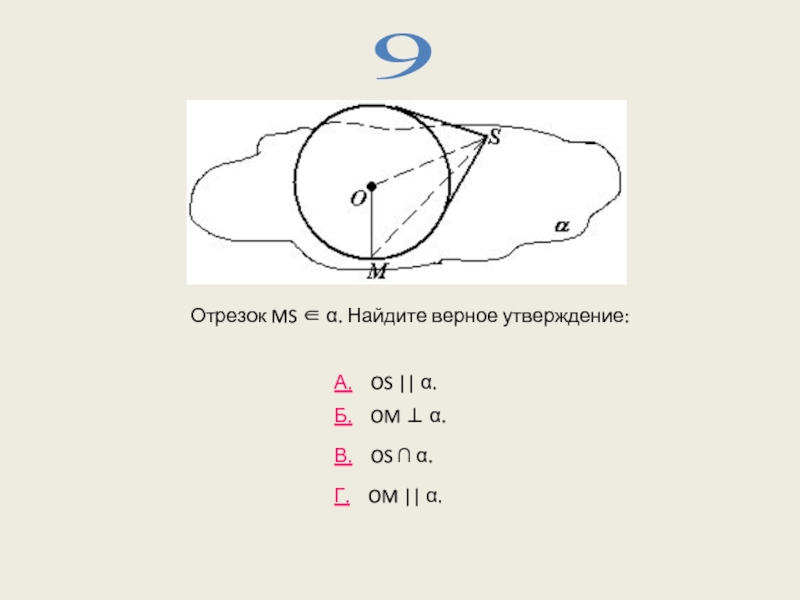
- 16. 9 А. OS || α. Б.
- 17. 10 А. Образующая конуса перпендикулярна высоте.
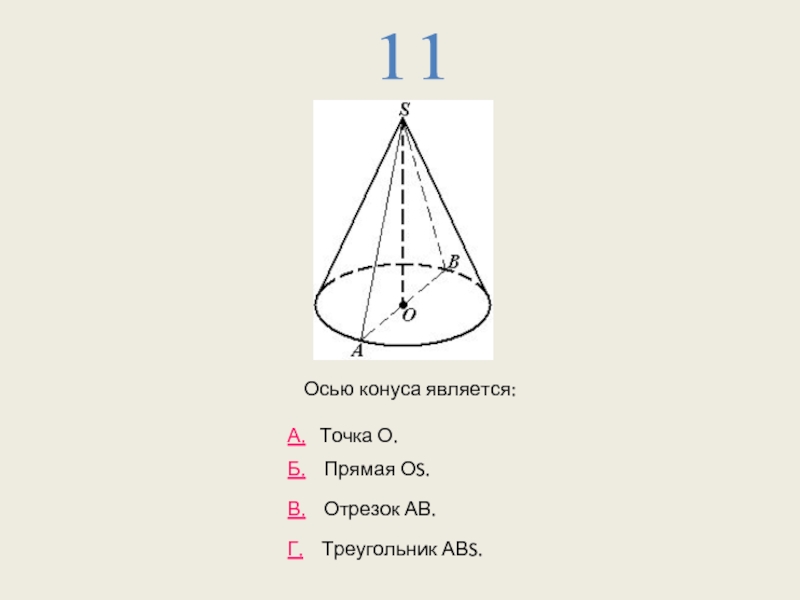
- 18. 11 А. Точка О. Б.
- 19. 12 А. Вращением ΔABS вокруг оси
- 20. 7. Проверка
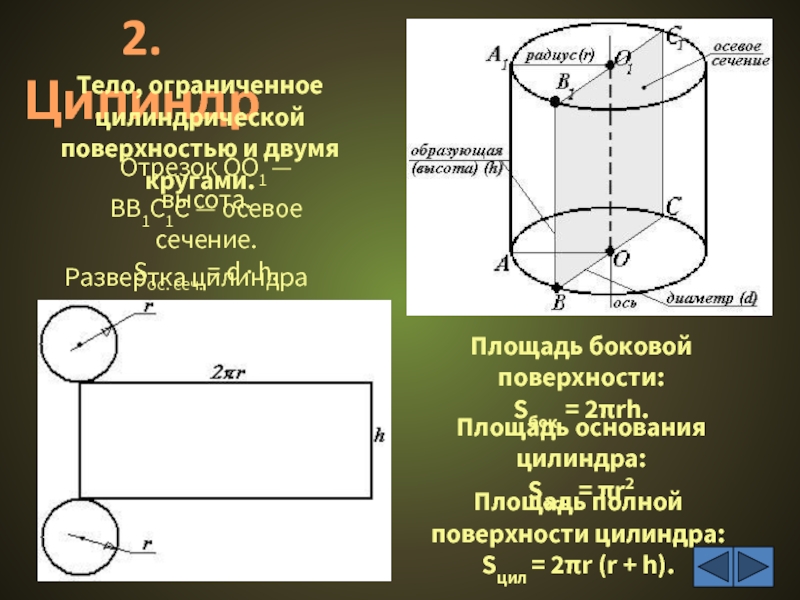
Слайд 3Отрезок ОО1 — высота.
ВВ1С1С — осевое сечение.
Sос. сеч. = d ·
Площадь боковой поверхности:
Sбок = 2πrh.
Площадь полной поверхности цилиндра:
Sцил = 2πr (r + h).
Развертка цилиндра
2. Цилиндр
Площадь основания цилиндра:
Sосн = πr2
Тело, ограниченное цилиндрической поверхностью и двумя кругами.
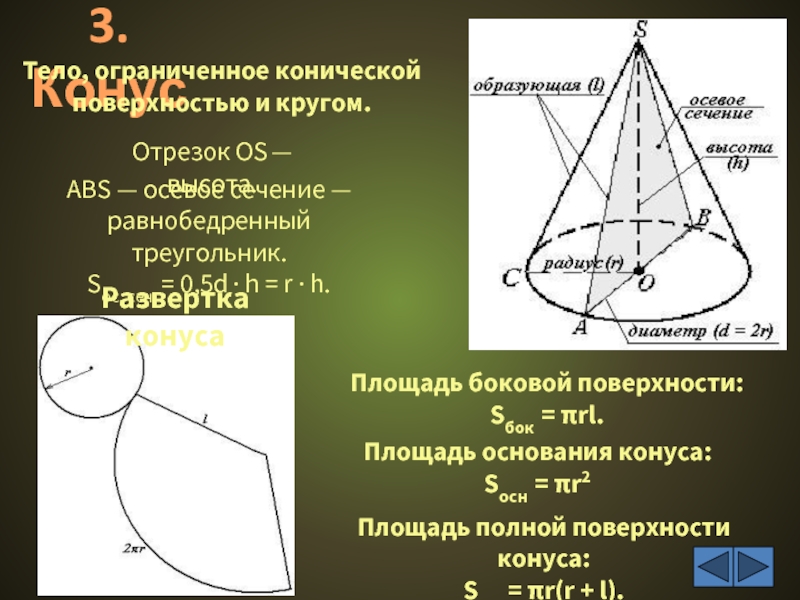
Слайд 4Отрезок ОS — высота.
AВS — осевое сечение — равнобедренный треугольник.
Sос. сеч.
Площадь боковой поверхности:
Sбок = πrl.
Площадь полной поверхности конуса:
Sкон= πr(r + l).
Развертка конуса
3. Конус
Тело, ограниченное конической поверхностью и кругом.
Площадь основания конуса:
Sосн = πr2
Слайд 5Осевое сечение — круг радиусом R.
Sос. сеч. = πR2.
Площадь поверхности сферы:
Sсф
Сферу развернуть
НЕЛЬЗЯ!
4. Сфера
Тело, ограниченное сферической поверхностью.
Уравнение сферы:
(x – x0)2 + (y – y0)2 + (z – z0)2 = R2
Слайд 6Задачка для маляра: сколько краски необходимо, чтобы покрасить детский «грибок», если
Решение:
1) Sпов = Sкон + Sцил = πRl + 2 π rh = 3 π + 1,5 π = 4,5 π ≈ 14,13 м2.
2) mкраски = Sпов · расход = 1413 г = 1,413 кг.
5. Для чего используем?
Слайд 76. Тест
В тетради пронумеруйте 12 вопросов (в строчку).
Под номером вопроса будем
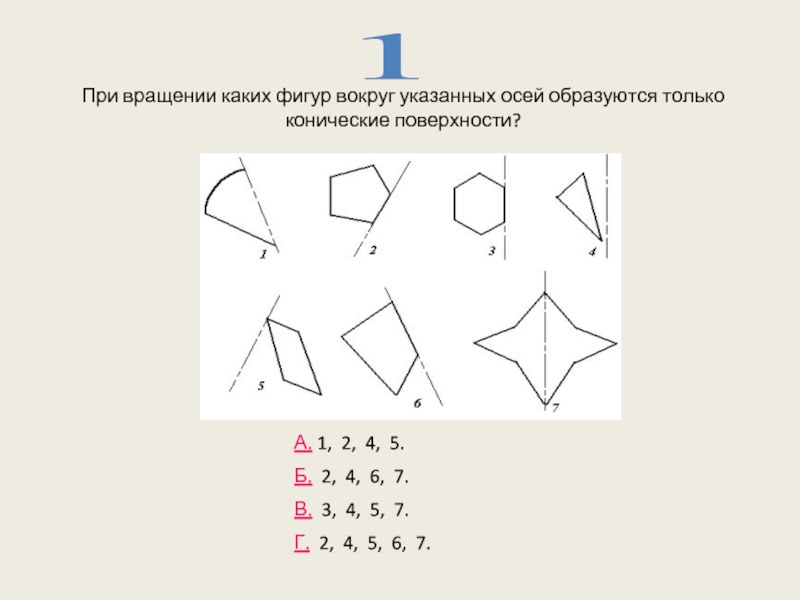
Слайд 8При вращении каких фигур вокруг указанных осей образуются только конические поверхности?
1
А.
Б. 2, 4, 6, 7.
В. 3, 4, 5, 7.
Г. 2, 4, 5, 6, 7.
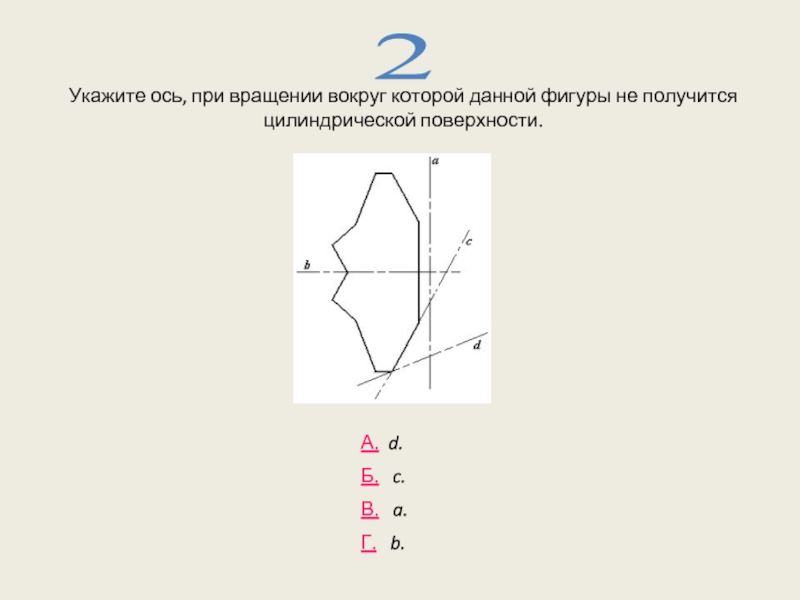
Слайд 9Укажите ось, при вращении вокруг которой данной фигуры не получится цилиндрической
2
А. d.
Б. c.
В. a.
Г. b.
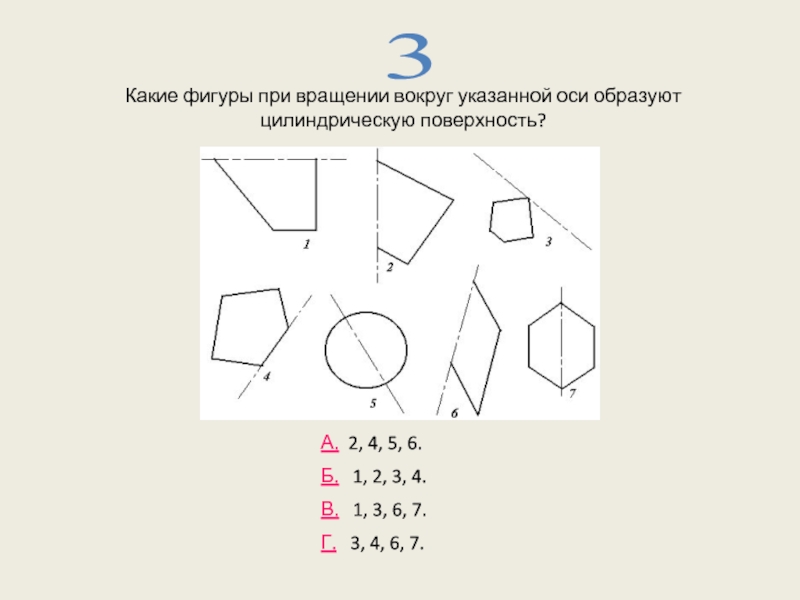
Слайд 10Какие фигуры при вращении вокруг указанной оси образуют цилиндрическую поверхность?
3
А. 2,
Б. 1, 2, 3, 4.
Г. 3, 4, 6, 7.
В. 1, 3, 6, 7.
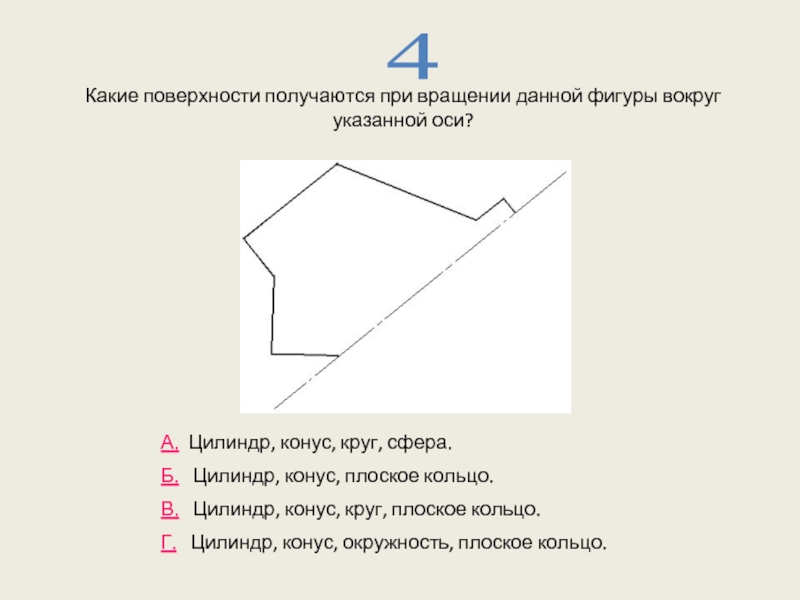
Слайд 11Какие поверхности получаются при вращении данной фигуры вокруг указанной оси?
4
А. Цилиндр,
Б. Цилиндр, конус, плоское кольцо.
В. Цилиндр, конус, круг, плоское кольцо.
Г. Цилиндр, конус, окружность, плоское кольцо.
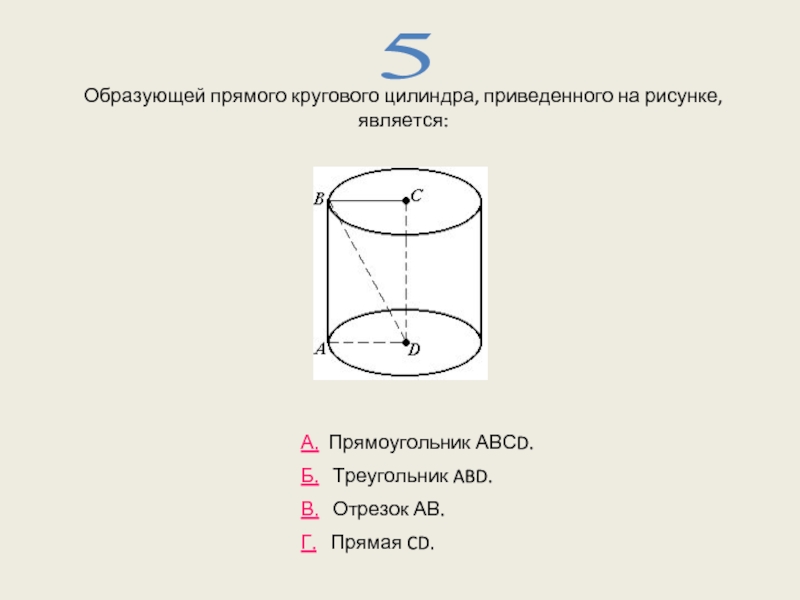
Слайд 12Образующей прямого кругового цилиндра, приведенного на рисунке, является:
5
А. Прямоугольник АВСD.
Б.
В. Отрезок АВ.
Г. Прямая CD.
Слайд 13Радиусом прямого кругового цилиндра, приведенного на рисунке, считают:
6
А. Отрезок ОВ.
Б.
В. Отрезок АВ.
Г. Отрезок О1В.
Слайд 14Высотой прямого кругового цилиндра, приведенного на рисунке, считают:
7
А. Прямую ОО1.
Б.
В. Отрезок АО1.
Г. Отрезок АО.
Слайд 1710
А. Образующая конуса перпендикулярна высоте.
Б. Образующая конуса перпендикулярна основанию.
В.
Г. Радиус основания конуса перпендикулярен высоте.
Найдите верное утверждение:
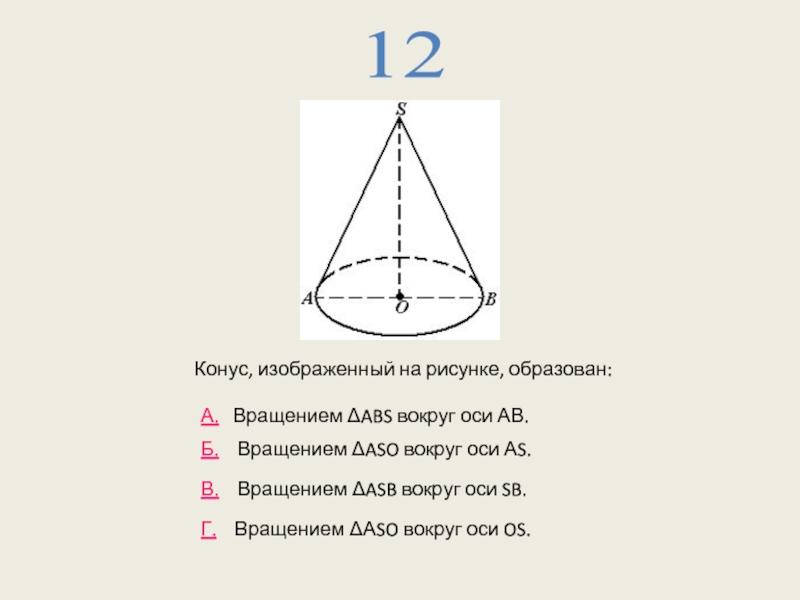
Слайд 1912
А. Вращением ΔABS вокруг оси АВ.
Б. Вращением ΔASO вокруг
В. Вращением ΔASB вокруг оси SB.
Г. Вращением ΔАSO вокруг оси OS.
Конус, изображенный на рисунке, образован: