- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Структура данных Scapegoat Tree презентация
Содержание
- 1. Структура данных Scapegoat Tree
- 2. Разработана Arne Andersson, Igal Galperin, Ronald L.
- 3. Определение
- 4. Понятия, необходимые для работы с данным деревом:
- 5.
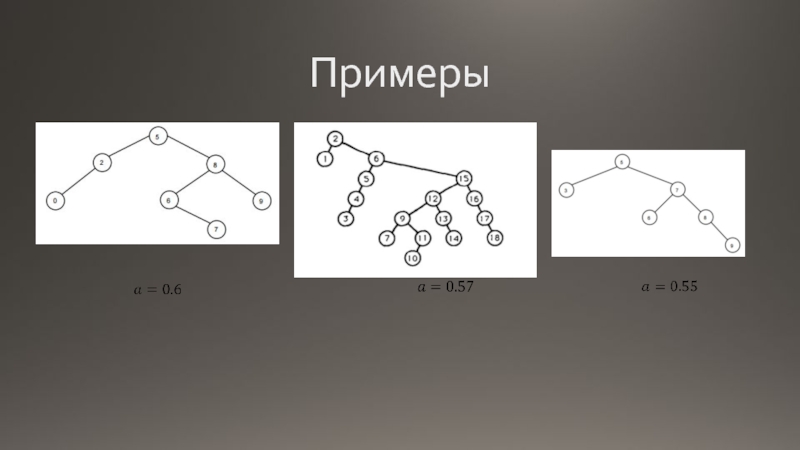
- 6. Примеры
- 7. Плюсы и минусы Scapegoat дерева Плюсы
- 8. Минусы В худшем случае операции модификации дерева
- 9. Поиск
- 10. Вставка Начинается вставка нового элемента в Scapegoat-дерево
- 11. Перебалансировка Обходим всё поддерево Scapegoat-вершины (включая её
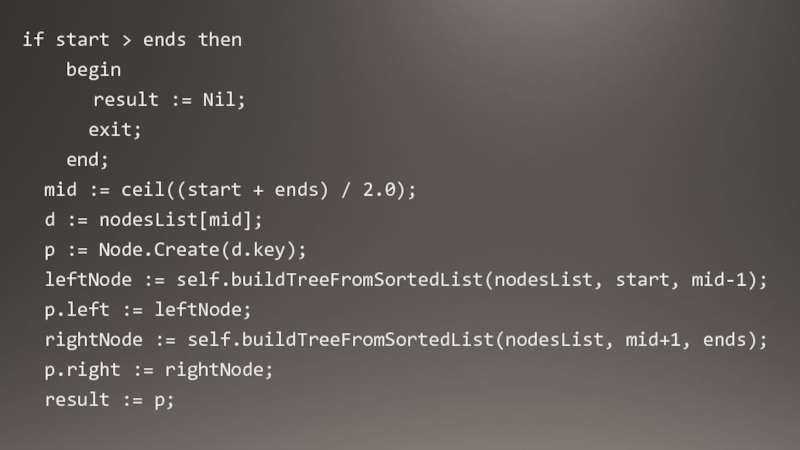
- 12. if start > ends then
- 13. 7 3 8 1 10 2 9
- 14. 8 1 Вычислив медиану (2) (start =
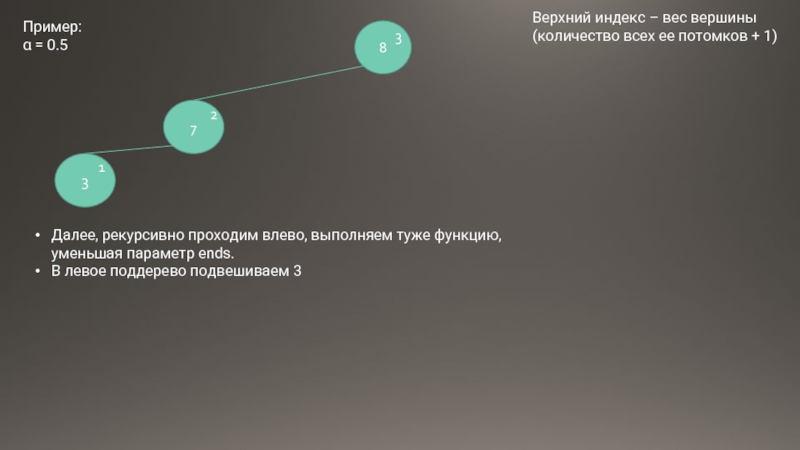
- 15. 8 7 1 2 Далее, рекурсивно проходим
- 16. 8 7 2 3 Далее, рекурсивно проходим
- 17. 8 7 2 4 Далее, рекурсивно проходим
- 18. 8 7 2 5 Далее, рекурсивно проходим
- 19. Удаление Удаляем вершину обычным удалением вершины бинарного
Слайд 2Разработана Arne Andersson, Igal Galperin, Ronald L. Rivest в 1962г.
Ronald L.
Arne Andersson
Слайд 4Понятия, необходимые для работы с данным деревом:
?−дерево
????[?]−корень дерева
????[?],???ℎ?[?]−левые и правый "сын" вершины
????ℎ??(?)− брат вершины (имеет общего родителя)
????ℎ(?)−глубина вершины (расстояние от вершины до корня)
ℎ???ℎ?(?)−глубина дерева ?
????(?)−вес вершины ? (кол−во всех ее дочерних вершины+1)
????[?]−размер дерева ? (вес корня)
???_size[T] – максимальный размер дерева T.
Слайд 7Плюсы и минусы Scapegoat дерева
Плюсы
Скорость одних операций возможно улучшить за
Scapegoat tree работает быстрее, чем красно-черное дерево и декартово.
Требуется меньше памяти (не надо хранить информацию для балансировки).
Настройки скорости меняются в процессе выполнения.
Не требуется перебалансировать дерево при поиске.
Слайд 8Минусы
В худшем случае операции модификации дерева могут занять ?(?) времени.
В
Слайд 10Вставка
Начинается вставка нового элемента в Scapegoat-дерево классически: поиском ищем место, куда
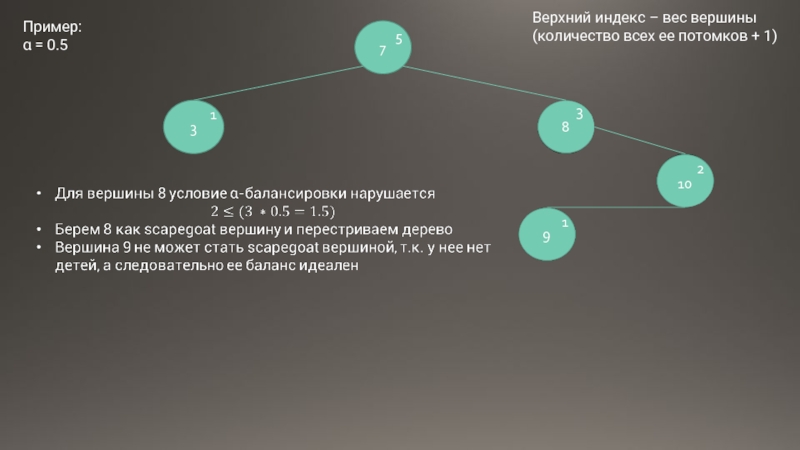
Легко понять, что это действие могло нарушить α-балансировку по весу для одной или более вершин дерева. И вот теперь начинается то, что и дало название структуре данных: мы ищем «козла отпущения» (Scapegoat-вершину) — вершину, для которой потерян α-баланс и её поддерево должно быть перестроено.
Сама только что вставленная вершина, хотя и виновата в потере баланса, «козлом отпущения» стать не может — у неё ещё нет «детей», а значит её баланс идеален.
Соответственно, нужно пройти по дереву от этой вершины к корню, пересчитывая веса для каждой вершины по пути. Если на этом пути встретится вершина, для которой критерий α-сбалансированности по весу нарушился — мы полностью перестраиваем соответствующее ей поддерево так, чтобы восстановить α-сбалансированность по весу.
Слайд 11Перебалансировка
Обходим всё поддерево Scapegoat-вершины (включая её саму) с помощью in-order обхода
Находим медиану на этом отрезке, подвешиваем её в качестве корня поддерева.
Для «левого» и «правого» поддерева рекурсивно повторяем ту же операцию.
Слайд 12if start > ends then
begin
result
exit;
end;
mid := ceil((start + ends) / 2.0);
d := nodesList[mid];
p := Node.Create(d.key);
leftNode := self.buildTreeFromSortedList(nodesList, start, mid-1);
p.left := leftNode;
rightNode := self.buildTreeFromSortedList(nodesList, mid+1, ends);
p.right := rightNode;
result := p;
Слайд 148
1
Вычислив медиану (2) (start = 0, ends = 4), подвешиваем 8
Пример:
α = 0.5
Верхний индекс – вес вершины
(количество всех ее потомков + 1)
Слайд 158
7
1
2
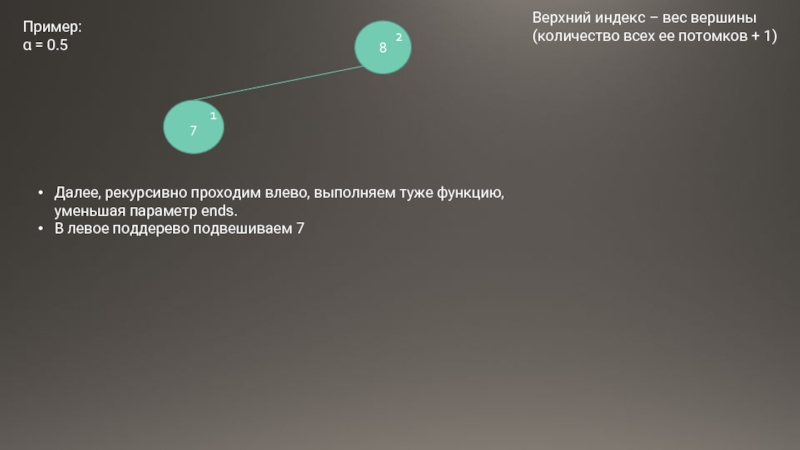
Далее, рекурсивно проходим влево, выполняем туже функцию, уменьшая параметр ends.
В левое
Пример:
α = 0.5
Верхний индекс – вес вершины
(количество всех ее потомков + 1)
Слайд 168
7
2
3
Далее, рекурсивно проходим влево, выполняем туже функцию, уменьшая параметр ends.
В левое
Пример:
α = 0.5
Верхний индекс – вес вершины
(количество всех ее потомков + 1)
3
1
Слайд 178
7
2
4
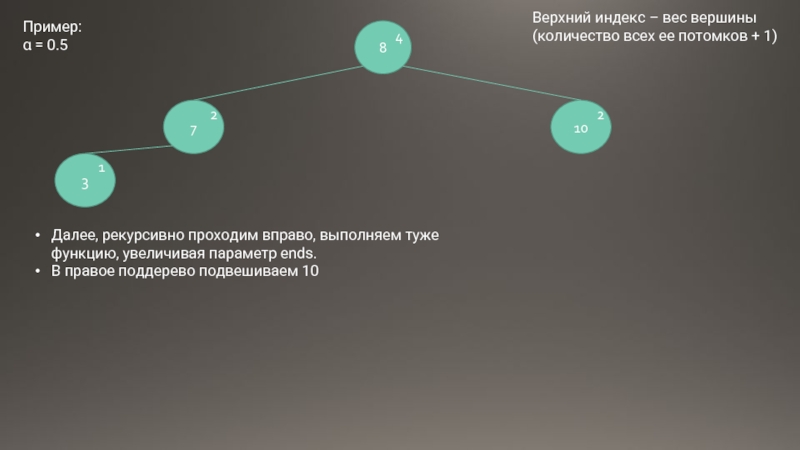
Далее, рекурсивно проходим вправо, выполняем туже функцию, увеличивая параметр ends.
В правое
Пример:
α = 0.5
Верхний индекс – вес вершины
(количество всех ее потомков + 1)
3
1
10
2
Слайд 188
7
2
5
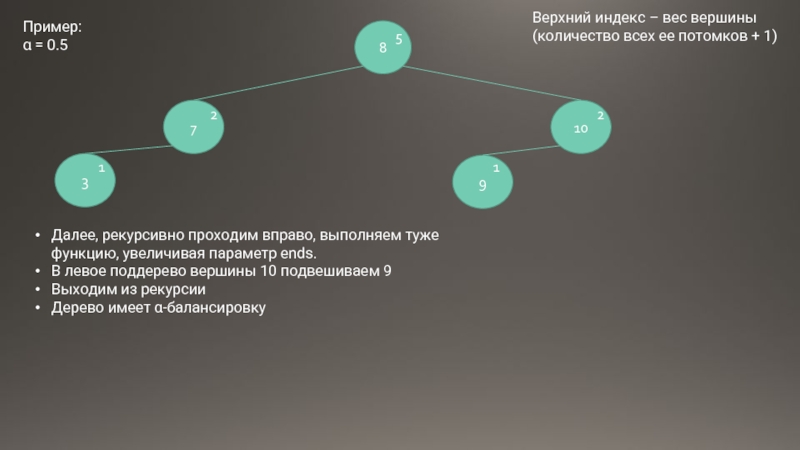
Далее, рекурсивно проходим вправо, выполняем туже функцию, увеличивая параметр ends.
В левое
Выходим из рекурсии
Дерево имеет α-балансировку
Пример:
α = 0.5
Верхний индекс – вес вершины
(количество всех ее потомков + 1)
3
1
10
2
9
1
Слайд 19Удаление
Удаляем вершину обычным удалением вершины бинарного дерева поиска (поиск, удаление, возможное
Далее проверяем выполнение условия
size[T] < α * max_size[T]
Если оно выполняется — дерево могло потерять α-балансировку по весу, а значит нужно выполнить полную перебалансировку дерева (начиная с корня) и присвоить max_size[T] = size[T]



![Понятия, необходимые для работы с данным деревом: ?−дерево ????[?]−корень дерева ? ????[?],???ℎ?[?]−левые и правый](/img/tmb/3/245692/b69c348d83cf712ef4fd7d48a2f4c46b-800x.jpg)